| [1] | Determination of Plasma Position using Poloidal Flux Loops and Comparison with Magnetic Probes Measurement in IR-T1 Tokamak, A. Salar Elahi et al., IEEE Trans. Plasma Science 38 (2), 181-185, (2010) |
| [2] | A Modified Flux Loop for Determination of Plasma Position in IR-T1 Tokamak, A. Salar Elahi et al., IEEE Trans. Plasma Science 38 (9), 3163-3167, (2010) |
| [3] | Analytical and Experimental Approach in Plasma Displacement Measurement in IR-T1 Tokamak, M. Emami, M. Ghoranneviss, A. Salar Elahi and A. Rahimi Rad, J. Plasma Phys. 76 (1), 1-8, (2009) |
| [4] | A Novel Technique for the Measurement of Plasma Displacement in IR-T1 Tokamak, A. Salar Elahi et al., Fusion Engineering and Design 85, 724–727, (2010) |
| [5] | Comparison between Flux Loops and Magnetic Probes in Determination of Shafranov Parameter in IR-T1 Tokamak, A. Salar Elahi et al., Phys. Scripta 80, 045501, (2009) |
| [6] | Two Experimental Methods for Measurement of Plasma Displacement in IR-T1 Tokamak, A. Salar Elahi et al., Phys. Scripta 80, 055502, (2009) |
| [7] | Time Evolution of the Energy confinement Time, Internal Inductance and Effective Edge Safety Factor on IR-T1 Tokamak, A. Salar Elahi et al., Phys. Scripta 81 (5), 055501, (2010) |
| [8] | Experimental Determination of Plasma Position Based on Two Analytical Methods in IR-T1 Tokamak, A. Salar Elahi et al., Phys. Scripta 82, 025502, (2010) |
| [9] | The First Results of Electrode Biasing Experiments in the IR-T1 Tokamak, M. Ghoranneviss, A. Salar Elahi et al., Phys. Scripta 82 (3), 035502, (2010) |
| [10] | Theoretical and Experimental Approach in Poloidal Beta and Internal Inductance Measurement on IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 346-349, (2009) |
| [11] | Effects of Resonant Helical Field (RHF) on Equilibrium Properties of IR-T1 Tokamak Plasma, A. Salar Elahi et al., J. Fusion Energy 28 (4), 416-419, (2009) |
| [12] | Effects of Resonant Helical Field on Plasma Internal Inductance in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 408-411, (2009) |
| [13] | RHF Effect on Shafranov Parameter and Shafranov Shift in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 412-415, (2009) |
| [14] | Measurement of Plasma Energy Confinement Time in Presence of Resonant Helical Field in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 394-397, (2009) |
| [15] | Measurement of Plasma Poloidal Beta in Presence of Resonant Helical Field in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 404-407, (2009) |
| [16] | Two Semi-Empirical Methods for Determination of Shafranov Shift in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 390-393, (2009) |
| [17] | Comparative Measurements of Plasma Position Using Multipole Moments Method and Analytical Solution of Grad–Shafranov Equation in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 28 (4), 385-389, (2009) |
| [18] | Comparison between Discrete Magnetic Coils and Multipole Coils for Measurement of Plasma Displacement in IR-T1 Tokamak, A. Rahimi Rad, M. Ghoranneviss, M. Emami, and A. Salar Elahi, J. Fusion Energy 28 (4), 420-426, (2009) |
| [19] | Plasma Magnetic Fluctuations Measurement on the Outer Surface of IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 1-4, (2010) |
| [20] | Investigation of Effects of Toroidal Field Ripple on Plasma Poloidal Beta in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 22-25, (2010) |
| [21] | TF Ripple Effects on Plasma Energy Confinement Time in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 29-31, (2010) |
| [22] | Measurement of the Shafranov Parameter in Presence of the Toroidal Field Ripple in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 26-28, (2010) |
| [23] | Study of Effects of the Effective Edge Safety Factor on the Energy confinement Time in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 32-35, (2010) |
| [24] | Experimental Study of Effects of the Internal Inductance on the Energy Confinement Time in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 36-40, (2010) |
| [25] | Plasma Horizontal Displacement Measurement Using Flux Loops in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 62-64, (2010) |
| [26] | Determination of the Plasma Internal Inductance and Evaluation of its Effects on Plasma Horizontal Displacement in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 76-82, (2010) |
| [27] | Demonstration of Shafranov Shift by the Simplest Grad–Shafranov Equation Solution in IR-T1 Tokamak, A. Rahimi Rad, M. Emami, M. Ghoranneviss, A. Salar Elahi, J. Fusion Energy 29 (1), 73-75, (2010) |
| [28] | Effects of Alfvenic Poloidal Flow and External Vertical Field on Plasma Position in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 83-87, (2010) |
| [29] | Relations between the Plasma Diamagnetic Effect and Plasma Basic Parameters in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (1), 88-93, (2010) |
| [30] | Differences between the Toroidal and Poloidal Flux loops in the Measurement of Plasma Position in Tokamaks, A. Salar Elahi et al., J. Fusion Energy 29 (3), 209-214, (2010) |
| [31] | Measurements of the Plasma Current Density and Q-Profiles in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (3), 232-236, (2010) |
| [32] | A Simplified Technique for the Determination of Plasma Displacement in IR-T1 Tokamak, A. Salar Elahi et al., J. Fusion Energy 29 (3), 251-255, (2010) |
| [33] | Comparative Measurements of the Asymmetry Factor in Tokamaks using the Magnetic Probes, Poloidal and Toroidal Flux Loops, A. Salar Elahi et al., J. Fusion Energy 29 (3), 279-284, (2010) |
| [34] | Design, Construction, and Installation of Movable Electrode Biasing System on the IR-T1 Tokamak, M. Ghoranneviss, A. Salar Elahi et al., J. Fusion Energy 29 (5), 467-470, (2010) |
| [35] | Biasing Effect on Modifying of the Tokamak Plasma Horizontal Displacement, A. Salar Elahi et al., J. Fusion Energy 29 (5), 461-465, (2010) |
| [36] | Measurement of the Plasma Boundary Shift and Approximation of the Magnetic Surfaces on the IR-T1 Tokamak, A. Salar Elahi et al., Brazilian J. of Physics 40 (3), 323-326, (2010) |
| [37] | A Novel Optical Technique based on Image Processing for Determination of Tokamak Plasma Displacement, A. Salar Elahi et al., J. Fusion Energy 30 (2), 116-120, (2011) |
| [38] | Effect of Limiter Biasing on Runaway electrons in Tokamaks, M.R. Ghanbari, M. Ghoranneviss, A. Salar Elahi et al., Phys. Scripta 83, 055501, (2011) |
| [39] | Multipole Moments based Study on Determination of Toroidal Plasma Equilibrium Position and Shift, A. Salar Elahi, J of Fusion Energy 30 (6), 477-480, (2011) |
| [40] | Determination of Tokamak Plasma Displacement based on Vertical Field Coil Characteristics, A. Salar Elahi et al., Fusion Engineering and Design 86, 442–445, (2011) |
| [41] | Analytical Technique for Determination of Toroidal Plasma Displacement, A. Salar Elahi et al., J of Fusion Energy 31 (2), 191-194, (2011) |
| [42] | Measurement of Runaway Electrons Energy by Hard X-ray Spectroscopy in a Small Circular Cross-section Tokamak, M.R. Ghanbari, M. Ghoranneviss, A. Salar Elahi and S. Mohammadi, Radiation Effects & Defects in Solids 166 (10), 789–794, (2011) |
| [43] | Design and Manufacturing of the Electrode Biasing System for the Tokamak, A. Salar Elahi et al., IEEE Trans. Plasma Science 40 (3), 892-897, (2012) |
| [44] | First Results of Movable Limiter Experiments and its Effects on the Tokamak Plasma Confinement, A. Salar Elahi et al., Accepted for publication in Radiation Effects & Defects in Solids (January 2012), DOI: 10.1080/10420150.2011.650171 |
| [45] | Investigation of Tokamak Plasma Fluctuations using Power Spectrum and FFT Analysis of Mirnov Coils Oscillations, Z. Goodarzi, M. Ghoranneviss and A. Salar Elahi, Accepted for the publication in J Fusion Energy (March 2012), DOI: 10.1007/s10894-012-9526-4 |
| [46] | Controlling the Energy of Runaway Electrons by Emissive Limiter Biasing in Tokamaks, M.R. Ghanbari, M. Ghoranneviss, A. Salar Elahi et al., Phys. Scripta 85 (5), 055502, (2012) |
| [47] | Laser Fusion Energy from  with Minimized Radioactivity, M. Ghoranneviss, A. Salar Elahi, H. Hora, G.H. Miley et al., Accepted for the publication in Laser and Particle Beams (May 2012), DOI: 10.1017/S0263034612000341 with Minimized Radioactivity, M. Ghoranneviss, A. Salar Elahi, H. Hora, G.H. Miley et al., Accepted for the publication in Laser and Particle Beams (May 2012), DOI: 10.1017/S0263034612000341 |
| [48] | Design and Fabrication of Emissive Biased Limiter and its Effect on Tokamak Plasma, M. Ghoranneviss et al., Accepted for the publication in Radiation Effects and Defects in Solids (June 2012) |
| [49] | New Approaches on Application of Multipole Moments for Determination of Toroidal Plasma Shift, A. Salar Elahi et al., Accepted for the publication in Radiation Effects and Defects in Solids (June 2012), DOI: 10.1080/10420150.2012.706609 |
| [50] | Design and Construction of Hot Limiter Biasing System for the Tokamak, A. Salar Elahi et al., Accepted for the publication in Radiation Effects and Defects in Solids (June 2012), DOI: 10.1080/10420150.2012.706607 |
| [51] | Estimating of Time dependence of Edge Plasma Turbulence in IR-T1 Tokamak, K. Mikaili, M. Ghoranneviss, A. Salar Elahi et al., Accepted for the publication in J Fusion Energy (July 2012), DOI: 10.1007/s10894-012-9563-z |

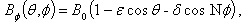
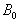 is the toroidal magnetic field at center of the tokamak chamber,
is the toroidal magnetic field at center of the tokamak chamber, 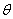 and
and 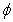 are poloidal and toroidal angles respectively,
are poloidal and toroidal angles respectively, 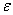 is the inverse aspect ratio,
is the inverse aspect ratio, 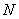 is the number of the toroidal field coils, and
is the number of the toroidal field coils, and 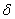 is the amplitude of the TF ripple where defined as:
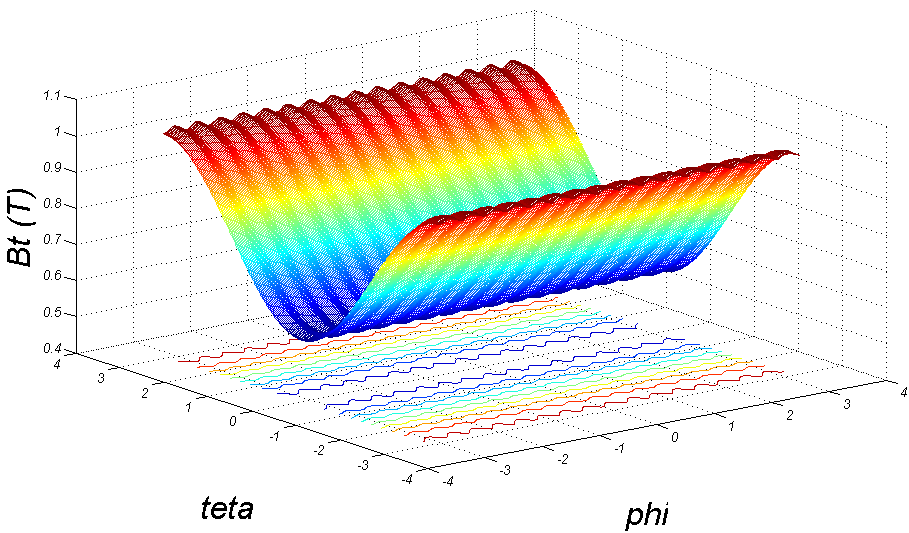
is the amplitude of the TF ripple where defined as: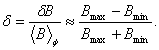
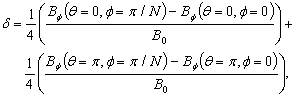
 (see Fig. (2)). Distributions of the tangential and normal magnetic fields can be written in the first order of the inverse aspect ratio as follows, respectively[1-5]:
(see Fig. (2)). Distributions of the tangential and normal magnetic fields can be written in the first order of the inverse aspect ratio as follows, respectively[1-5]: 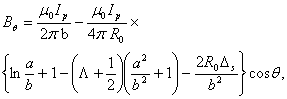
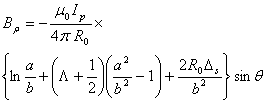
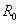 is the major radius of the vacuum vessel,
is the major radius of the vacuum vessel, 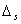 is the Shafranov shift,
is the Shafranov shift, 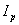 is the plasma current,
is the plasma current, 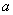 and
and 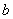 are the minor plasma radius and minor chamber radius respectively. These equations accurate for low
are the minor plasma radius and minor chamber radius respectively. These equations accurate for low 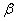 plasma, large aspect ratio, and circular cross section tokamaks as IR-T1, and where:
plasma, large aspect ratio, and circular cross section tokamaks as IR-T1, and where: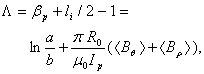
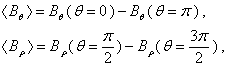
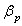 is the poloidal beta and
is the poloidal beta and 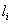 is the plasma internal inductance. We measured
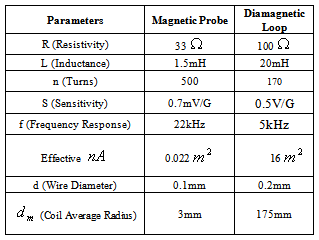
is the plasma internal inductance. We measured 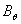 and
and 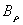 which are the contribution of the plasma current to the equilibrium field, after compensating the vacuum field and integrating of the output signals of magnetic probes. The major approximations in our work are that we suppose the plasma minor radius defined by limiter radius, namely
which are the contribution of the plasma current to the equilibrium field, after compensating the vacuum field and integrating of the output signals of magnetic probes. The major approximations in our work are that we suppose the plasma minor radius defined by limiter radius, namely 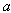 is constant, and also the TF ripple amplitude at different poloidal angles is constant, whereas the toroidal flux is no constant as a function of phi, and then we have to have field lines which loop back on themselves, in which case we have to have localized poloidal currents. Experimental results will be presented in the section 5.
is constant, and also the TF ripple amplitude at different poloidal angles is constant, whereas the toroidal flux is no constant as a function of phi, and then we have to have field lines which loop back on themselves, in which case we have to have localized poloidal currents. Experimental results will be presented in the section 5.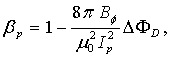
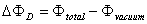 is the diamagnetic flux. By substituting the Eq. (1) in the Eq. (8) we have:
is the diamagnetic flux. By substituting the Eq. (1) in the Eq. (8) we have: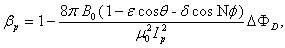
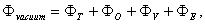 and where
and where 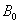 is the toroidal magnetic field in the absence of the plasma and center of chamber which can be measured using the Ampere law,
is the toroidal magnetic field in the absence of the plasma and center of chamber which can be measured using the Ampere law, 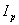 is the plasma current,
is the plasma current, 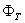 is the toroidal flux because of toroidal field coils,
is the toroidal flux because of toroidal field coils, 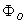 and
and 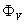 are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop, and
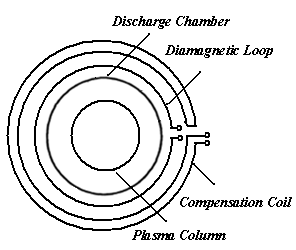
are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop, and 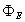 is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated with compensation coil (see Fig. (3)) and also using dry runs technique. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received (see Figs. (2),(3)). Therefore, according to above two sections we can find the internal inductance. From Eq. (6) we have:
is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated with compensation coil (see Fig. (3)) and also using dry runs technique. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received (see Figs. (2),(3)). Therefore, according to above two sections we can find the internal inductance. From Eq. (6) we have: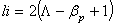
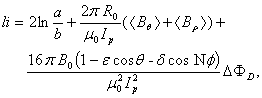
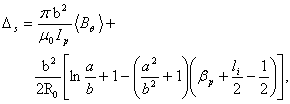
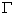 of the radius
of the radius 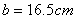 in angles of
in angles of 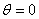 and
and 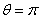 to detect the tangential component of the magnetic field
to detect the tangential component of the magnetic field 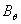 , and two magnetic probes are also installed above,
, and two magnetic probes are also installed above, 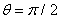 , and below,
, and below, 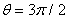 , to detect the normal component of the magnetic field
, to detect the normal component of the magnetic field 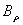 , as shown in Fig. (2).
, as shown in Fig. (2).
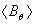 and
and 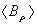 from magnetic probes,
from magnetic probes, 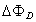 from diamagnetic loop,
from diamagnetic loop, 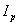 from Rogowski coil and substituting them in to Eq. (9), Eq. (11), and Eq. (12), the poloidal beta, internal inductance, and Shafranov shift and also the effects of TF ripple on them measured. Experimental results presented in the next section.
from Rogowski coil and substituting them in to Eq. (9), Eq. (11), and Eq. (12), the poloidal beta, internal inductance, and Shafranov shift and also the effects of TF ripple on them measured. Experimental results presented in the next section. 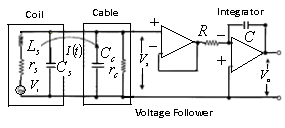
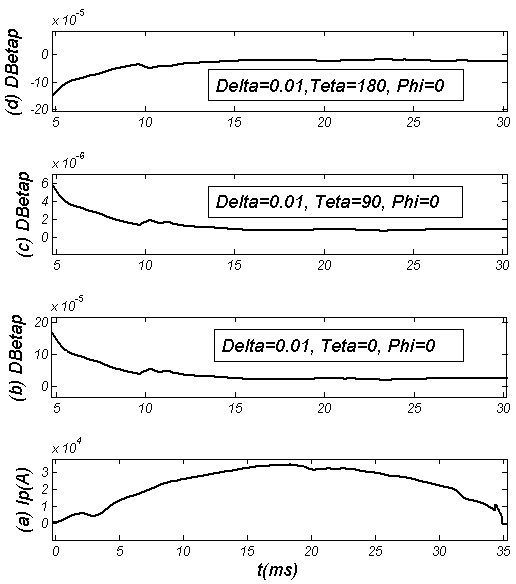
 . Also in the high field side region (
. Also in the high field side region ( ) the difference is negative, whereas in low field side (
) the difference is negative, whereas in low field side ( ) the difference is positive.
) the difference is positive.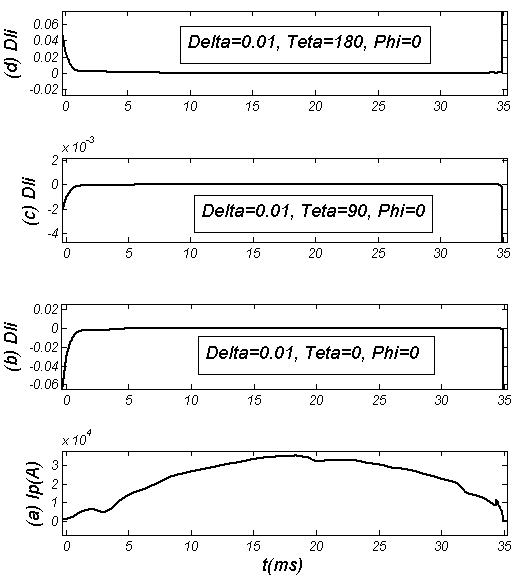
 . Also in the high field side region (
. Also in the high field side region ( ), unlike the poloidal beta case, the difference is positive, whereas in low field side (
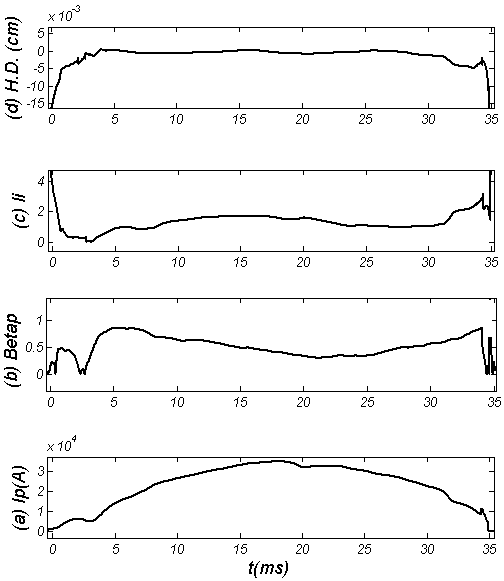
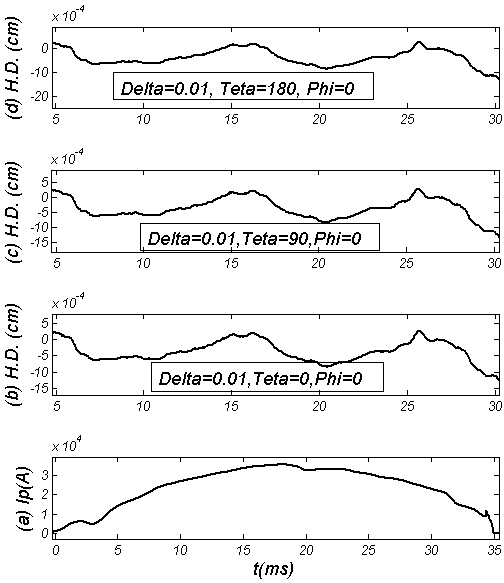
), unlike the poloidal beta case, the difference is positive, whereas in low field side (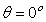 ) the difference is negative.In the Figure (9), the effects of TF ripple amplitude on the Horizontal Displacement (H.D.) at different poloidal angles presented. No difference observed.
) the difference is negative.In the Figure (9), the effects of TF ripple amplitude on the Horizontal Displacement (H.D.) at different poloidal angles presented. No difference observed.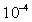 , and also in the high field side region the difference is negative, whereas in the low field side the difference is positive. Another results is that difference between the internal inductance in presence of the TF ripple and in absence of the TF ripple is in order of the
, and also in the high field side region the difference is negative, whereas in the low field side the difference is positive. Another results is that difference between the internal inductance in presence of the TF ripple and in absence of the TF ripple is in order of the 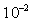 , and also in the high field side region unlike the poloidal beta case, the difference is positive, whereas in low field side the difference is negative. In the Shafranov shift, no difference observed. Also no sensible variation observed in the Shafranov shift due to the TF ripple on IR-T1 tokamak plasma. The major approximations in our work are that we suppose the plasma minor radius is constant and also the TF ripple amplitude at different poloidal angles is constant, whereas the toroidal flux is no constant.
, and also in the high field side region unlike the poloidal beta case, the difference is positive, whereas in low field side the difference is negative. In the Shafranov shift, no difference observed. Also no sensible variation observed in the Shafranov shift due to the TF ripple on IR-T1 tokamak plasma. The major approximations in our work are that we suppose the plasma minor radius is constant and also the TF ripple amplitude at different poloidal angles is constant, whereas the toroidal flux is no constant. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
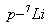 with Minimized Radioactivity, M. Ghoranneviss, A. Salar Elahi, H. Hora, G.H. Miley et al., Accepted for the publication in Laser and Particle Beams (May 2012), DOI: 10.1017/S0263034612000341
with Minimized Radioactivity, M. Ghoranneviss, A. Salar Elahi, H. Hora, G.H. Miley et al., Accepted for the publication in Laser and Particle Beams (May 2012), DOI: 10.1017/S0263034612000341