-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2012; 2(5): 107-111
doi: 10.5923/j.jnpp.20120205.01
On the Structure of A=3 Nuclei
Syed Afsar Abbas , Shakeb Ahmad
Department of Physics, Aligarh Muslim University, Aligarh, 202 002, India
Correspondence to: Syed Afsar Abbas , Department of Physics, Aligarh Muslim University, Aligarh, 202 002, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A=3 is the lightest genuine “nucleus” with an “inside” with a centre and an outside/surface. As A=2 nucleus does not have an “inside” what transpires in A=3 to make this happen? The hole in the charge distribution of 3He is a major problem in the A=3 nuclei. The canonical wave function of A=3 nuclei which does well for the electromagnetic properties of A=3 nuclei fails to produce the hole in A=3 nuclei. We show that this wave function does give the surface while the “inside” is completely missed by it. The reproduction of the inside of the A=3 nuclei demands that a different wave function be used. This new wave function gives these A=3 nuclei a mathematical centre which arises fundamentally and which also reproduces the hole in 3He. Thus this hybrid wave function, given in terms of the nucleonic degrees of freedom, provides us with a better and a consistent understanding of the structure of the A=3 nuclei.
Keywords: Nuclear Structure, Helion/Triton, Charge Distribution, Clustering
Cite this paper: Syed Afsar Abbas , Shakeb Ahmad , "On the Structure of A=3 Nuclei", Journal of Nuclear and Particle Physics, Vol. 2 No. 5, 2012, pp. 107-111. doi: 10.5923/j.jnpp.20120205.01.
1. Introduction
- Clusters are playing an important role in the current nuclear physics. Of these α-clusters are known to play a prominent role. These are known to be spontaneously emitted from heavy nuclei. Other clustering in particular A=3 clustering is also possible and this was recently studied in detail by us[1]. Strong experimental evidences of clustering of A=3 nuclei- 3He (Helion) and 3H (Triton) were pointed out and a consistent theoretical understanding was attempted therein. One would have thought that nuclei as simple as A=3 should have been well understood by now. But in keeping with the complexity in the structure of another three body system that of baryons made up of three quarks things are not all that easy.There are deficiencies as to the agreement between the experimental and the conventional nuclear models in explaining the ground state properties of light nuclei. For example, calculations of the binding energies for the few particle systems such as 3H, 3He and 4He, using as inputs various two-body potentials only, show an under binding relative to their corresponding experimental values. Several mechanisms have been proposed to minimize the deficiencies between the experiments and the theoretical models. One of the most important of these is the effect of the three-body interactions, which cannot be deduced from the two-body data. This may give the necessary components to the ground state properties of A=3 nuclei. Within the nonrelativistic framework of nuclear physics a three-body force is expected to have an appreciable contribution relative to other mechanisms, especially for systems with cluster structures. The importance of three-body forces in nuclear physics is well known, and quantum Monte Carlo (QMC) calculations of light nuclei have provided evidence in its favour. There the A=3 systems can be described as a three-body quantum cluster entity where the dominant three body forces acts between two neutrons and a proton or between two protons and a neutron. Thus there has been growing evidence in nuclear physics that three-body forces should exist among the nucleons inside nuclei, for a large number of isotopes[2-5].A major goal of nuclear physics is to understand the correct nature of the many-body interactions. Being the fundamental theory of strong interaction, Quantum Chromo dynamics is still unable to quantitatively describe the two-nucleon interactions from the first principle, specially, in the non perturbative regime of low energy nuclear physics. Further, the two-body potentials constructed, by using the large amount of experimental data on nucleon-nucleon scattering are inadequate to explain the ground state properties as well as many of two-body scattering data. The composite nature of the nucleons, indicates that many-nucleon forces, and at the least the three-nucleon forces are necessary to explain many bound state properties. A lot of effort has been devoted to understand the correct nature of nuclear forces and currents and this has resulted in developments of accurate many-body techniques for evaluating them[2-19].There are other features of the nuclear matter which point to the need of real three-body force. For finite nuclei one needs a real three-body force in order to reproduce the spin-orbit splitting between the single particle orbits[14]. There are indeed pointers from the experiments and the theory which hint that a real three-body force may be needed in shell model studies as well. For example, the inclusion of a real three-body force gives the correct spin assignment in case of 10B[15]. The differential cross sections for the γ+ 4He → p+ t reaction were measured as a function of photon-beam energy and proton-scattering angle and are compared with the latest model calculations. At 0.6-1.2 GeV, the data is in good agreement only with the calculations that include three-body mechanisms, thus confirming their importance. These results reinforce the conclusion of some previous study of the three-body break-up of 3He that demonstrated the great importance of the three-body mechanisms in the energy region 0.5-0.8 GeV[11-13]. DAPHNE Collaboration have measured the differential cross sections for the 3He (γ, pd) reaction. The results confirm the rapid decrease of forward-angle cross sections with increasing photon energy, whilst at backward angles, aided by the high precision of the measurement, which show the clear enhancement in the angular distribution and is a possible signature of three-body mechanisms[17]. Also a schematic three-body forces in addition to a general two-body forces leads to a strongly improved description of the energies of light and medium mass nuclei[18], and there are effects of three-body force on the longitudinal response function of 4He[19]. Further, while trying to fit the nuclear matter binding energy and density simultaneously the results of the best two body interactions, all fall on the so called Coester band. No matter what we do, if one confines oneself to two body interaction then there is no way one can do any better? This clearly hints at including at least a three body force[3BF]. There are also several strong reasons as to why it seems that it is not enough to confine ourself to only two body interactions. For example, there are basic phenomenological reasons[20] why a three body force is needed and also more fundamental reasons[21] for the same. Note that these 3BF can not be reduced to any two body force and thus have their own independent existence.The realization that in nonrelativistic framework 3BF is indispensable in a complete and consistent description of nuclei has grown in recent years. One knows that A=3 bound states 3H and 3He are theoretically underbound using only NN (two body) forces. So also is 4He underbound and this is represented by the so called Tjon lines[22]. Proper inclusion of 3BF in different models is essential to fit the binding energies of all 3H, 3He and 4He[22]. The same paper also indicated that the presence of four-body forces (4BF) is ruled out for 4He.This point is very succinctly made by Wringa and Peiper[23] “Modern nucleon nucleon (NN) potentials, such as the Argonne v18, CD Bonn, Reid93, NijmI, and NijmII, fit over 4300 elastic NN scattering data with a χ2=1. These potentials are very complicated, including spin, isospin, tensor, spin-orbit, quadratic momentum-dependent, and charge-dependent tensor, with ~ 40 parameters adjusted to fit the data. Despite this sophistication, these potentials can not reproduces the binding energy of few body nuclei such as 3H and 3He without the assistance of a three-nucleon potential”.Hence we see that the 3BF manifest itself right away in the structure of A=3 nuclei, so much so that it is not possible to fit triton's and helion's binding energy, rms radii etc. without involving a 3BF[22-23]. Note that at the same time they also found that 4BF in α-nucleus is negligible[22].Experiments confirm our prediction, based on multi quarks in QCD, of a tendency for triton clustering in light neutron rich nuclei[24]. As such the neutron halo phenomena are naturally explained[25]. Prediction of exotic molecular states rich in triatomic clusters is made through new Ikeda-like diagram configurations for the nuclei
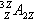 . Recent experiments clearly demonstrate the importance of the excited state 2+ at 1.8 MeV in the substructure 6He for the ground state of the nucleus 8He. This means that the ground state structure of 8He rather than being α + 4n is actually 3H + 3H +2n. Is there some new symmetry which supports this tritonic clustering? We know that n and p combine to give a bound triplet state (S=1, T=0). It has no excited states. The singlet state (S=0, T=1) is unbound by 64 keV. This being isospin partner of (n-n) (S=0, T=1) and (p-p) (S=0, T=1), all these are unbound. Here we proposed a new symmetry called the "mucosin" with h and t belonging to the fundamental representation of this new and distinct SU (2) group[25]. The binding energies of 3He and 3H are 7.72 MeV and 8.48 MeV, respectively and also these two have no excited states. Hence for low-energy excitations, we may consider these as elementary. That is we treat h and t as elementary particles with a new “isospin ". Hence, we would expect for (h-t) the triplet (S=1, T=0) to be bound and singlet (S=0, T=1) to be unbound. Also, its isospin partners (h-h) (S=0, T=1) and (t-t) (S=0, T=1) would be unbound too. This puts triton clustering in nuclei on a stronger pedestal.Hence we see that three body-force is essential for the consistent understanding of the nuclear phenomena. Clearly the 3BF does not even exist in the A=2 system, i.e. in N-N scattering or in the A=2 deuteron ground state. But the 3BF raises his head right away in the A=3 nuclei themselves. So, clearly in the A=3 nuclei both the 2BF and the 3BF are acting. What basic and fundamental difference is introduce in the A=3 nuclei? It is clear that the A=2 system is only a “surface” with no “inside” component. On the other hand the A=3 is the lightest nucleus with an additional “inside”. This hints that the “inside” in this nucleus must be a result of the 3BF. We wish to study this effect in this paper. Does the “inside” in the A=3 nucleus is anything to do with the 3BF? If so, how does it manifest itself physically? We show below that indeed the “hole” in the A=3 nuclei as well as the creation of the unique “centre” of the A=3 nucleus is a manifestation of the 3BF. We shall show that this physical effect is ensured by the mathematical property of the wave function at the centre of the A=3 nucleus.
. Recent experiments clearly demonstrate the importance of the excited state 2+ at 1.8 MeV in the substructure 6He for the ground state of the nucleus 8He. This means that the ground state structure of 8He rather than being α + 4n is actually 3H + 3H +2n. Is there some new symmetry which supports this tritonic clustering? We know that n and p combine to give a bound triplet state (S=1, T=0). It has no excited states. The singlet state (S=0, T=1) is unbound by 64 keV. This being isospin partner of (n-n) (S=0, T=1) and (p-p) (S=0, T=1), all these are unbound. Here we proposed a new symmetry called the "mucosin" with h and t belonging to the fundamental representation of this new and distinct SU (2) group[25]. The binding energies of 3He and 3H are 7.72 MeV and 8.48 MeV, respectively and also these two have no excited states. Hence for low-energy excitations, we may consider these as elementary. That is we treat h and t as elementary particles with a new “isospin ". Hence, we would expect for (h-t) the triplet (S=1, T=0) to be bound and singlet (S=0, T=1) to be unbound. Also, its isospin partners (h-h) (S=0, T=1) and (t-t) (S=0, T=1) would be unbound too. This puts triton clustering in nuclei on a stronger pedestal.Hence we see that three body-force is essential for the consistent understanding of the nuclear phenomena. Clearly the 3BF does not even exist in the A=2 system, i.e. in N-N scattering or in the A=2 deuteron ground state. But the 3BF raises his head right away in the A=3 nuclei themselves. So, clearly in the A=3 nuclei both the 2BF and the 3BF are acting. What basic and fundamental difference is introduce in the A=3 nuclei? It is clear that the A=2 system is only a “surface” with no “inside” component. On the other hand the A=3 is the lightest nucleus with an additional “inside”. This hints that the “inside” in this nucleus must be a result of the 3BF. We wish to study this effect in this paper. Does the “inside” in the A=3 nucleus is anything to do with the 3BF? If so, how does it manifest itself physically? We show below that indeed the “hole” in the A=3 nuclei as well as the creation of the unique “centre” of the A=3 nucleus is a manifestation of the 3BF. We shall show that this physical effect is ensured by the mathematical property of the wave function at the centre of the A=3 nucleus.2. Objectives
- To understand the clustering of A=3 nuclei we have to see what aspects are the ones which contribute to its clustering property. Hence a better and consistent understanding of the structure of A=3 is required.What is the structure of A=3 nucleus vis a viz A=2 nucleus and even A=1 nucleon? Although in general one considers A=2 deuteron as the first nucleus, in structure is resembles A=1 nucleon rather than A=3 and heavier nuclei. This is clearly manifested in the similarity of the form factors of proton and that of deuteron which both fall of smoothly (with no undulation)[26, 27]. So these both are pure “surface” nuclei with nothing like an “inside” in it. But a typical nucleus as we know has Fermi charge distribution with a distinct inside and a distinct surface. The form factor of 3He (in contrast to A=1 & A=2 form factors) has an oscillatory pattern[26] thereby including an “inside” and an “outside/surface”. A=3 is the lightest nucleus showing this characteristics and hence should be treated as the lightest nucleus.What changes as we go from the A=2 to the A=3 that an additional “inside” to an already existing “outside” is created in the A=3. An outside also means that, somehow this light system is able to create a “centre” of the A=3 nucleus. For heavier nuclei we justify a self bound nucleus as arising from a Hartree-Fock self consistent calculations which produces self consistently a central potential for large number of nucleons which also justifies shell structure etc. But the A=3 is much too small and this logic cannot hold here. Not to forget that the A=2 deuteron does not have an “inside” and a centre. The A=1 & A=2 are bound due to proper symmetrisation of all degrees of freedom relative to nucleon and deuteron, respectively. So for the A=3 one cannot or should not invoke a potential concept and so we are forced to seek an explanation of this dual characterisation, an “inside” with a centre and an “outside/surface” in terms of proper wave functions. What wave function of the A=3 will give this dual characterisation of the A=3 nucleus? Also we want to know how the 3BF arises phenomenologically. Afterall the 3BF acts in the A=3 nucleus and not in the A=2 system!
3. Our Model
- To understand as to what makes A=3 so special, let us study the two properties of the ground state magnetic moment of 3He and 3H, and next the 3He charge density.The degrees of freedom relevant for 3He and 3H are spin, isospin and orbital space. The total wave function should be anti-symmetric. For three nucleons the spin wave function in standard notation are of mixed symmetry
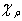 and
and 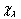 where
where 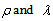 correspond to mixed symmetric state with the first two spins in anti-symmetric and symmetric states respectively. The corresponding mixed symmetric states or the three nucleons are
correspond to mixed symmetric state with the first two spins in anti-symmetric and symmetric states respectively. The corresponding mixed symmetric states or the three nucleons are 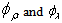 . If we ensure full anti-symmetry in spin-isospin space
. If we ensure full anti-symmetry in spin-isospin space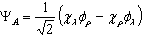 | (1) |
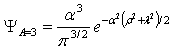 | (2) |
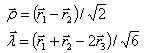 | (3) |
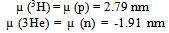 | (4) |
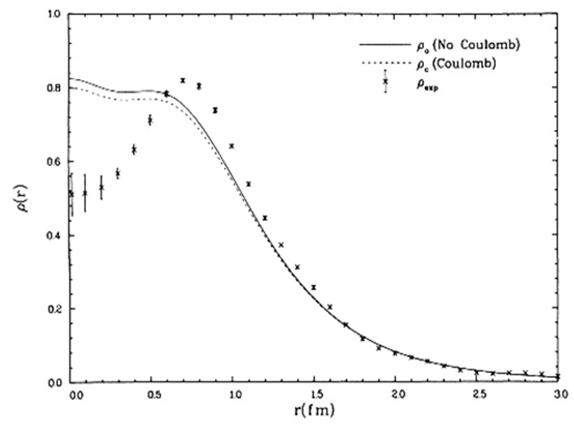 | Figure 1. Point nucleon 3He theoretical charge density and the corresponding experimental density indicated as data points[28] |
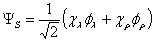 | (5) |
 [30][p.31] (the exact form of f is not important for our discussion here). Then the charge density is
[30][p.31] (the exact form of f is not important for our discussion here). Then the charge density is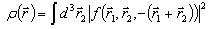 | (6) |
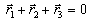 | (7) |
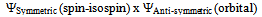 and thus the hole is naturally predicted by such a wave function.Note the
and thus the hole is naturally predicted by such a wave function.Note the 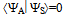 (from Esq. (1) and (5)) and thus the two parts of the wave function, one for r > r0 (for some suitable values say r0 ~ 1fm for 3He) and the other r < r0 with Eq. (5) would work well for both the magnetic moment etc. and for reproducing the charge/matter densities of A=3 nuclei, and thus is entirely within the nucleonic degree of freedom only.Hence both anti-symmetric and symmetric orbital parts play a complementary role in predicting the magnetic moment as well as the hole in A=3 nuclei. It is like two different phases (with orbital part anti-symmetric in one and completely different, that is symmetric, in the other one) coexisting for the same nucleus A=3.
(from Esq. (1) and (5)) and thus the two parts of the wave function, one for r > r0 (for some suitable values say r0 ~ 1fm for 3He) and the other r < r0 with Eq. (5) would work well for both the magnetic moment etc. and for reproducing the charge/matter densities of A=3 nuclei, and thus is entirely within the nucleonic degree of freedom only.Hence both anti-symmetric and symmetric orbital parts play a complementary role in predicting the magnetic moment as well as the hole in A=3 nuclei. It is like two different phases (with orbital part anti-symmetric in one and completely different, that is symmetric, in the other one) coexisting for the same nucleus A=3.4. Conclusions
- Summarising, note that the light nuclei A=1 and A=2 are all pure 'surface' nuclei. A genuine nucleus should have a distinct 'interior' plus a clear 'surface' outside. A=3 is hence, the first genuine nucleus. It has managed to build an "interior" while retaining the "surface". And the new structure suggested here plays a fundamental role in creating a first clear cut "interior" along with a centre (which appears as a hole) while still retaining the "surface" outside. Thus what is needed is a hybrid model with one part describing the outside and the surface while another orthogonal term giving the interior. Now producing the interior is highly non-trivial job. It is so as it has to produce a point inside which should become a centre. This has to be ensured mathematically and this is what our function does. Note that all this is done entirely within nucleonic degrees of freedom itself.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML