-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
2012; 2(4): 77-86
doi: 10.5923/j.jnpp.20120204.01
The Role of Electron Capture and Energy Exchange of Positively Charged Particles Passing Through Matter
1Dept. of Radiation physics, Klinikum Muenchen-Pasing and MPI of Physics, Goettingen, Germany
2Work has been partially presented on the occasion of the Annual Meeting of ICRU 2010 at WPE, Essen, Germany
Correspondence to: W. Ulmer , Dept. of Radiation physics, Klinikum Muenchen-Pasing and MPI of Physics, Goettingen, Germany.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The conventional treatment of the Bethe-Bloch equation for protons accounts for electron capture at the end of the projectile track by the small Barkas correction. This is only a possible way for protons, whereas for light and heavier charged nuclei the exchange of energy and charge along the track has to be accounted for by regarding the projectile charge q as a function of the residual energy. This leads to a significant modification of the Bethe-Bloch equation, otherwise the range in a medium is incorrectly determined. The linear energy transfer (LET) in the Bragg peak domain and at the distal end is significantly influenced by the electron capture: Thus the stepwise filling operation of the electron shells along the particle track is treated by the Fermi energy EF of Fermi-Dirac statistics and leads to the conversion of carbon ions from C6+ at the beginning of the track to C1+ at the Bragg peak region. A rather significant consequence is that in the domain of the Bragg peak the superiority of carbon ions is reduced compared to protons.
Keywords: Bethe-Bloch Equation, Electron Capture, Fermi-Dirac Statistics, Radiotherapy with Carbon Ions
Article Outline
1. Introduction
- The application of the Bethe-Bloch equation (BBE) for the determination of the electronic stopping power is established for the passage of electrons and protons through homogeneous media. A particular importance of BBE appears in Monte-Carlo calculations to simulate the behaviour (energy transfer) of charged projectile particles along the track. This equation reads:
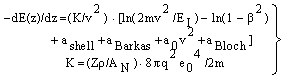 | (1) |
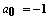 | (2) |
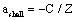 | (3) |
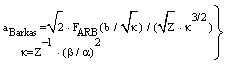 | (4) |
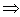 μ = m/(1+m/M), where M is the proton mass. However, this leads for protons to a rather small correction (i.e., less than 0.1 % for protons). For complex systems EI and some other contributions like ashell and aBarkas can only be approximately calculated by simple quantum-mechanical models (e.g., harmonic oscillator); the latter terms are often omitted and EI is treated as a fitting parameter, but different values are proposed and used[4]. The restriction to the logarithmic term leads to severe problems, if either v → 0 or 2m v2 /EI → 1. It should be added that a correct treatment of the electron capture removes the singularity of positively charged ions, since q2(E) → 0, if the residual energy E assumes zero.
μ = m/(1+m/M), where M is the proton mass. However, this leads for protons to a rather small correction (i.e., less than 0.1 % for protons). For complex systems EI and some other contributions like ashell and aBarkas can only be approximately calculated by simple quantum-mechanical models (e.g., harmonic oscillator); the latter terms are often omitted and EI is treated as a fitting parameter, but different values are proposed and used[4]. The restriction to the logarithmic term leads to severe problems, if either v → 0 or 2m v2 /EI → 1. It should be added that a correct treatment of the electron capture removes the singularity of positively charged ions, since q2(E) → 0, if the residual energy E assumes zero. 2. Methods
2.1. The Integration of BBE for Protons
- In the following, we consider at first the integration of BBE for protons, i.e. we consider the Barkas correction in the conventional way. In previous publications[25–26] we have presented an analytical integration of BBE, which is the physical base of the transport of protons and electrons. In order to obtain the integration of BBE, we start with the logarithmic term and perform the substitutions:
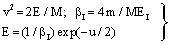 | (5) |
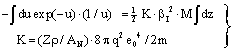 | (6) |
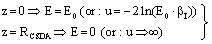 | (7) |
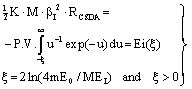 | (8) |
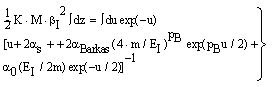 | (9) |
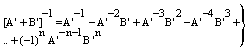 | (10) |
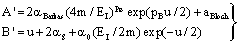 | (11) |
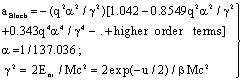 | (12) |
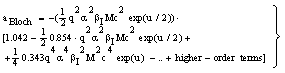 | (13) |
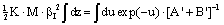 | (14) |
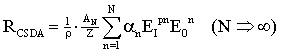 | (15) |
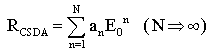 | (16) |
|
|
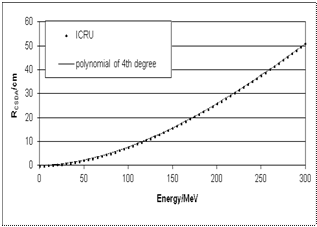 | Figure 1. Comparison data in[4] of proton RCSDA range (up to 300 MeV) in water and the fourth-degree polynomial (equation 16). The average deviation amounts to 0.0013 MeV |
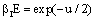 . A Gompertz- function is defined by:
. A Gompertz- function is defined by: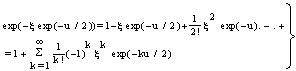 | (17) |
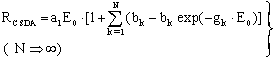 | (17a) |
|
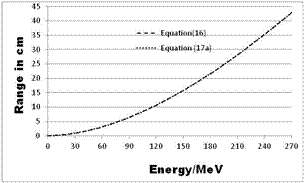 | Figure 2. RCSDA calculation - comparison between a fourth-degree polynomial (equation (16)) and two exponential functions (equation (17a)) |
2.2. The Inversion Problem: Calculation of E0(RCSDA) and E(z)
- Above formulas can also be used for the calculation of the residual distance RCSDA – z, relating to the residual energy E(z); we have only to perform the substitutions RCSDA → RCSDA – z and E0 → E(z) in these formulas. In various problems, the determination of E0 or E(z) as a function of RCSDA or RCSDA – z is an essential task. The power expansion implies again a corresponding series E0 = E0(RCSDA) in terms of powers:
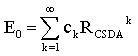 | (18) |
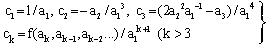 | (18a) |
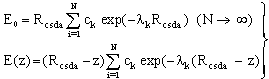 | (19) |
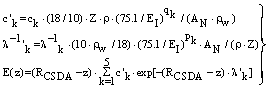 | (20) |
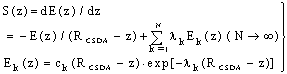 | (21) |
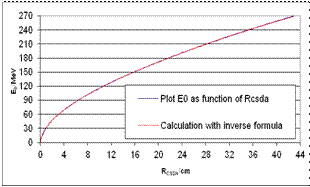 | Figure 3. Test of the inverse Formula (40) E0 = E0(RCSDA) by five exponential functions. The mean deviation amounts to 0.11 MeV; the plot results from Figure 1 |
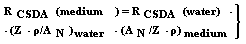 | (22) |
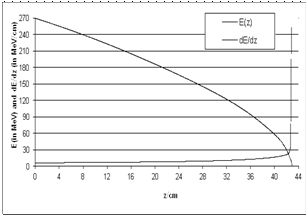 | Figure 4. E(z) and dE(z)/dz as a function of z (LET based on CSDA); energy straggling and electron capture are omitted |
2.3. Qualitative Properties of the Electron Transfer Described by BBE and Electron Capture
- According to BBE the energy spectrum produced by carbon ions should be the same as that produced by protons, and the only difference between protons and carbon ions should be the intensity of the released collision electrons, i.e. the amplification factor should be 36 for carbon ions. It is well-known that this property is not valid for the following reasons: The average ionization energy for carbon ions turned out to be EI = 80 eV instead of EI = 75 eV for protons[4, 29]. Paper[29] is based on investigations of some other authors[10, 19, 30, 31]. The second reason is the electron capture of the carbon ion. Thus a carbon ion can capture a free electron, which has been excited immediately before. Figure 5 shows this effect. However, only electrons with a slow relative velocity to the carbon ion can account for this process (vrelative ≈ 0). Since the transition time of the capture electron to a lower atomic state of the carbon ion is less than 10-10 sec with a simultaneous emission of light (UV or visible), it is possible that the captured electrons goes lost again, and only a stripping effect occurs for a short time. If the C6+ ions has been finally transferred to a stable C5+ ion, the identical process can be repeated until at the end track a neutral carbon atom is obtained having only a thermal energy. In the environment of the Bragg peak the effective charge of the carbon ion is about the same that of a proton, namely +e0. Since the electron capture can only occur for electrons of which the relative velocity is slow, the upper energy limit of the energy exchange Eex is the Fermi edge EF, which is for an electron gas not higher than the thermal energy kBT. If the charge of carbon ion amounts to +6·e0 and, at least, > +e0, the environmental atomic electrons suffer lowering of the energy levels due to the Coulomb interaction, which leads to an increase of EI. Therefore the stated value of EI = 80 eV represents an average value produced the fast carbon ion starting with +6·e0 and ending with an uncharged, neutral carbon atom.
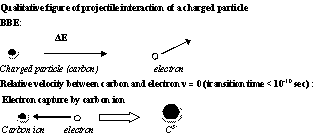 | Figure 5. Excitation of an atomic electron by the collision interaction of a fast carbon ion with an atomic electron and the reversal process of the electron capture |
2.4. Application Fermi-Dirac Statistics to Electron Capture
- In the following it is the task to obtain a quantum statistical description of electron capture and stripping of electrons, i.e. those electrons which reduce the effective charge of the carbon ion for a short time and go lost before a transition to a stable atomic state of carbon can occur. For this purpose, we consider the quantum statistical energy exchange Eex between projectile particle such as proton, He ion or carbon ion. The related mathematical procedure can be used to describe processes like energy straggling, lateral scatter and energy/charge exchange between projectile ion and released electrons below the Fermi edge EF. However, before we can account for the latter problem we have to consider the related mathematical tools. In general, if H represents the Hamiltonian (either non-relativistic or relativistic) and f(H) an operator functions, then for continuous operators H the connection holds:
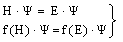 | (23) |
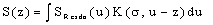 | (24) |
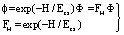 | (25) |
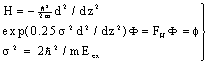 | (26) |
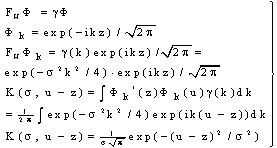 | (27) |
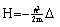 | (28) |
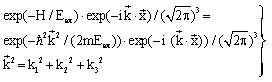 | (29) |
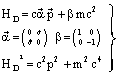 | (30) |
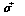 refers to the Pauli spin matrices (this should not be confused with the rms-value σ of a Gaussian distribution function). In position representation we obtain:
refers to the Pauli spin matrices (this should not be confused with the rms-value σ of a Gaussian distribution function). In position representation we obtain: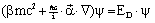 | (31) |
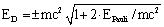 | (32) |
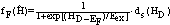 | (33) |
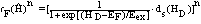 | (34) |
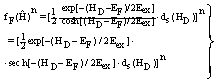 | (35) |
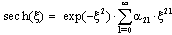 | (36) |
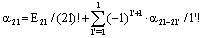 | (37) |
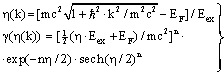 | (38) |
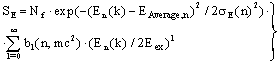 | (39) |
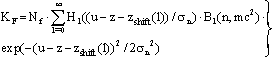 | (39a) |
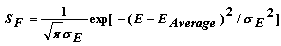 | (40) |
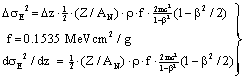 | (41) |
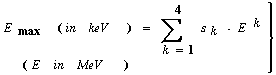 | (42) |
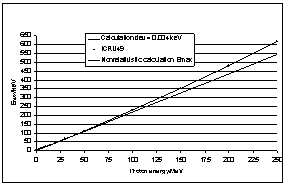 | Figure 6. Calculation of Emax according to equation (42). The straight line below refers to the non-relativistic limit |
|
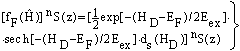 | (44) |
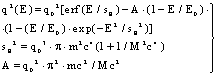 | (44a) |
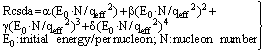 | (45) |
3. Results
- In the following we present results of calculations for protons, He ions and carbon ions; the initial energy amounts to 400 MeV/nucleon. This appears to be a reasonable restriction with regard to therapeutic conditions. Thus Figure 7 shows that at the end of the projectile track all charged ions nearly behave in the same manner.
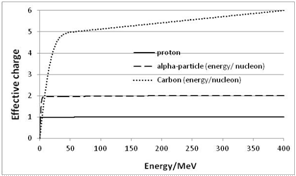 | Figure 7. Effective charge of protons, He- and C-ions as a function of the initial energy E0 (for protons, we have to assume qeff = 0.995) |
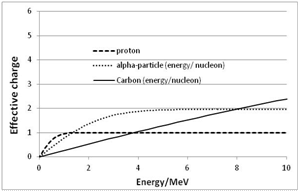 | Figure 8. Section of the above Figure 7 for E ≤ 10 MeV |
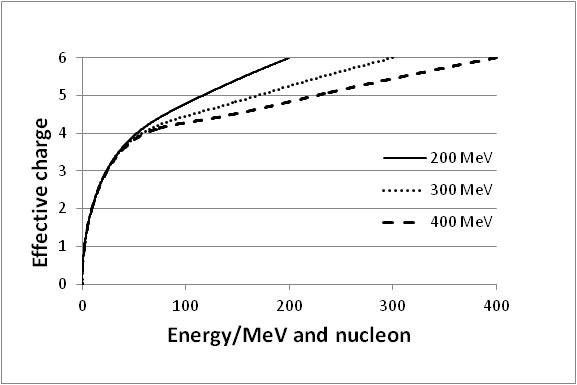 | Figure 9. Effective charge q(E) of carbon ions in dependence of the initial energy E0 for the cases E0 = 200, 300 and 400 MeV/nucleon |
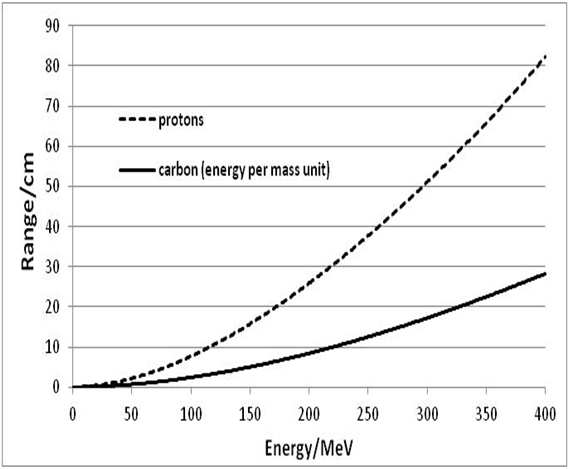 | Figure 10. Comparison between proton range calculated by Formula (16) and range of the carbon ion determined by Formula (45) |
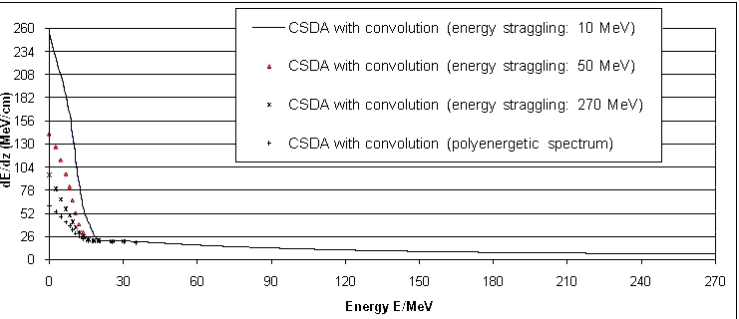 | Figure 11. Stopping power of protons in dependence of the energy straggling (mono-energetic and polychromatic protons without taking account of electron capture) |
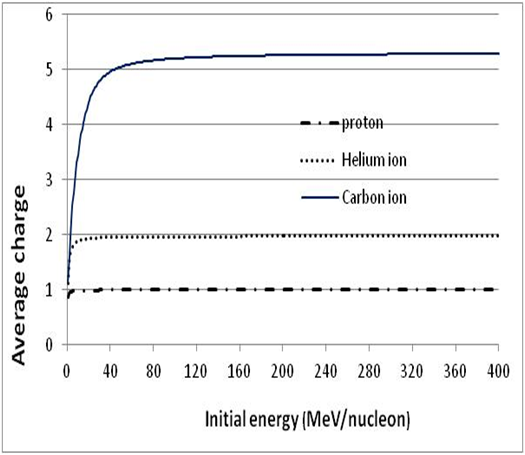 | Figure 12. Average charge of protons, He and C ions as a function of the initial energy E0 (for protons, we have to assume qeff = 0.995) |
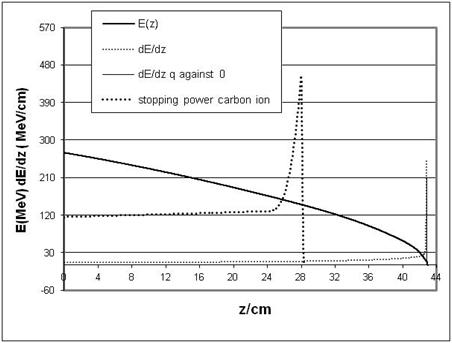 | Figure 13. LET for mono-energetic protons (dots) and overall stopping power S(z) of carbon ions 400 MeV/nucleon |
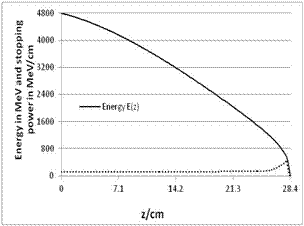 | Figure 14. LET of carbon ions (400 MeV/nucleon) |
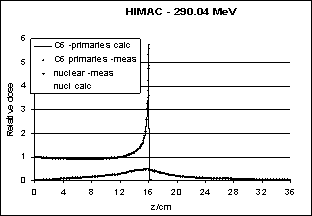 | Figure 15. Measurement (HIMAC) and theoretical calculation of the Bragg curve of carbon ions (290 MeV/nucleon) |
4. Conclusions
- The main purpose of this communication was the derivation of a systematic theory of electron capture of charged particles and the role for the LET. The role of the LET of light ions with regard to the biological effectiveness has recently been studied[34]. There are purely empirical trials to include charge capture in Monte-Carlo codes[10 – 13, 35 – 36]. However, it appears that a profound basis for the calculation of q2(E), E(z), S(z) and Rcsda(E0) depending besides the initial energy E0 also on the nuclear mass number N is required to account for further influences of Bragg curves such as the density of the medium and its nuclear mass/charge AN and Z. The unmodified use of BBE leads to wrong results and the Barkas correction, which does not affect the factor q2 of BBE, only works for protons or antiprotons, whereas for projectile particles like He or carbon ions this correction cannot be considered as small. The presented theory includes the Barkas effect without any correction model. In view of the enormous effort with reference to the acceleration of C6 ions, the application of this therapy modality should be critically reviewed.
ACKNOWLEDGEMENTS
- The author wishes to thank Dr. Barbara Schaffner. Due to her sabbatical work at HIMAC, Japan, the analysis of Figure 15 has been made available.
References
| [1] | Bethe H. A., Ashkin J. ‘‘Passage of radiations through matter’’ Experimental Nuclear Physics (E. Segrè Ed.) Wiley New York, 176 – 190, 1953. |
| [2] | Bloch F. ‘‘Zur Bremsung rasch bewegten Teilchen beim Durchgang durch Materie‘‘ Ann der Physik 16, 285 – 292, 1993. |
| [3] | Bethe H. A. ‘’Molière’s theory of multiple scattering’’ Phys. Rev. 89, 1256 - 1262, 1953. |
| [4] | ICRU ‘’Stopping powers and ranges for protons and α-particles’’ ICRU Report 49 (Bethesda, MD), 1993. |
| [5] | CERN-Report: Monte-Carlo code GEANT4 GEANT4-Documents, 2005. http//geant4.web.cern.ch/geant4/G4UsersDocuments/Overview/html. |
| [6] | Boon S. N. ‘’Dosimetry and quality control of scanning proton beams’’, PhD Thesis Rijks University Groningen, 1998. |
| [7] | Ashley J. C, Ritchie R. H., Brandt W. ‘’Document No. 021192‘’, (National Auxilliary Service, New York), 1974. |
| [8] | Barkas W.H., Dyer N.J., Heckmann H. H. ‘’Resolution of the Mass Anomaly’’ Phys. Rev. Letters 11, 26 – 29, 1963. |
| [9] | Betz H. D. ‘’Charge States and Charge-changing Cross Sections of Fast Heavy Ions Penetrating through Gaseous and Solid Media’’ Rev. Mod. Phys. 44, 465 – 85, 1972. |
| [10] | Dingfelder M., Hantke D., Inokute M., Paretzke H.G. ‘’A Monte-Carlo code for heavy charged ions‘’ Radiation Physics and Chemistry 53, 1 – 20, 1998. |
| [11] | Gudowska I., Sobolevsky N., Andreo P., Belkic D., Brahme A. ‘’Ion beam transport in tissue-like media using the Monte-Carlo code SHIELD-HIT’’ Phys. Med. Biol. 49, 1933 – 38, 2004. |
| [12] | Hollmark M., Uhrdin J., Belkic D., Gudowska I., Brahme A. ‘‘Influence of multiple scattering and energy loss straggling on the absorbed dose distributions of therapeutic light ion beams: 1. Analytical pencil beam model’’ Phys. Med. Biol..49, 3247 - 3067, 2004. |
| [13] | Hubert F., Bimbot R., Gaurin H. ‘’Range and stopping-power tables for 2.5 – 500 MeV/nucleon heavy ions in solids’’ Data Nucl. Data Tables 46, 1 – 213, 1990. |
| [14] | Kanai T., Kohno T., Minohara S., Sudou M., Takada E., Soga F., Kawachi K. Fukumura A. ‘’Dosimetry and measured differential W values of air heavy ions’’ Rad. Res. 135, 293 – 301, 1993. |
| [15] | Kusano Y., Kanai T., Yonai S., Komori M., Ikeda N., Tachikawa Y., Ito A. Uchida H. ‘’Field-size dependence of doses of therapeutic carbon beams’’ Med. Phys. 34, 4016 – 4022, 2007. |
| [16] | Mairani A. ‘’Nucleus-Nucleus Interaction Modeling and Applications in Ion Therapy Treatment Planning’’, PHD-Thesis, University of Pavia, 2007. |
| [17] | Matveev V. I., Sidorov D.B. ‘’Effective Stopping of Fast Heavy Highly Charged Structure Ions in Collisions with Complex Atoms’’ JETP Letters 84, 234 – 248, 2006. |
| [18] | Sigmund P. ‘’Charge dependent electronic stopping power of swift non-relativistic heavy ions’’ Phys. Rev. A56, 3781 – 3793, 1997 |
| [19] | Sigmund P., Schinner A. ‘‘Effective charge of heavy carbon ions‘‘ Nucl. Instruments and Methods B195, 64 - 70, 2002. |
| [20] | Sigmund P. ‘’Invited lectures presented at a symposium arranged by the Royal Danish Academy of Sciences and Letters Copenhagen’’, Edited by P. Sigmund Matematisk-fysiske Meddelelser 52 Det Kongelige Danske Videnskabernes Selskab, The Royal Danish Academy of Sciences and Letters Copenhagen, 2006. |
| [21] | Sihver L., Schardt D., Kanai T. ‘’Depth dose distributions of high-energy Carbon, Oxygen and Neon Beams in Water’’ Japanese Journal Med. Phys. 18, 1 – 21, 1998. |
| [22] | Yarlagadda B.S., Robinson J.E., Brandt W. ‘’Effective-Charge Theory and the Electronic Stopping Power of Solids’’ Phys. Rev. B17, 3473 – 82, 1978. |
| [23] | Zhang R., Newhauser W. D. ‘’Calculation of water equivalent thickness of materials of arbitrary density, elemental composition and thickness in proton beam irradiation’’ Phys. Med. Biol.. 54, 1383 – 95, 2009. |
| [24] | Ziegler J. F., Manoyan J. M. ‘’The Stopping of Ions in Compounds’’ Nuclear Instr. Meth. B35, 215 – 227. 1998. |
| [25] | Ulmer W. ‘’Theoretical aspects of energy range relations, stopping power and energy straggling of protons’’ Radiation physics and chemistry 76, 1089 – 1107, 2007. |
| [26] | Ulmer W., Matsinos E., 2010 ‘’Theoretical methods for the calculation of Bragg curves and 3D distribution of proton beams’’ European Physics Journal (ST), 190, 1 – 81, 2010. |
| [27] | Abramowitz M., Stegun I. ‘’Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables’’, Natural Bureau of Standards, 1970. |
| [28] | Feynman R.P. “Quantum electrodynamics - Lecture Notes and Reprints’’ (Benjamin, New York), 1962. |
| [29] | Paul H. “The mean ionization potential of water, and its connection to the range of energetic carbon ions in water’’ Nuclear Instruments and Methods in Physics Research B255, 435 – 437, 2007. |
| [30] | Bichsel H,, Hiraoka T., Omata K. ‘’Aspects of Fast-Ion Dosimetry’’ Radiation Research 153, 208 – 215, 2000 |
| [31] | Kraft G. ‘’Tumor therapy with heavy charged particles’’ Progress in Particle Nuclear Phys. 45, 473 – 544, 2000. |
| [32] | Ulmer W. ‘’Inverse problem of a linear combination of Gaussian convolution kernels (deconvolution) and some applications to proton/photon dosimetry and image processing’’ Inverse Problems 26,085002, 2010. |
| [33] | Ulmer W., Schaffner B. ‘’Foundation of an analytical proton beamlet model for inclusion in a general proton dose calculation system’’ Radiation physics and chemistry 80, 378 – 392, 2011. |
| [34] | Brahme A. ‘’Optimal use of light ions for radiation therapy’’ Radiol. Science 53, 35-61, 2010. |
| [35] | Brahme A. ‘’ Physical, Biological and Clinical Background for the Development of Biologically Optimized Light Ion Therapy’’, In: Technological bases for Radiation Therapy. Ed. Lewitt S & Purdy J., Springer, Heidelberg, 2011. |
| [36] | Lechner A., Ivanchenko V. ‘’Recent developments in GEANT4 heavy-ion stopping and their impact to ion ranges’’. CERN-report, available in web address: //http:G4SUWS_2009_Lechner_DevelopmentHeavy Ion_Stopping.pdf |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML