-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2012; 2(3): 71-76
doi: 10.5923/j.jnpp.20120203.06
Late Time Behavior of Unstable Particles
K. Urbanowski, J. Piskorski
University of Zielona Gora, Institute of Physics, ul. Prof. Z. Szafrana 4a, 65-516 Zielona Gora, Poland
Correspondence to: K. Urbanowski, University of Zielona Gora, Institute of Physics, ul. Prof. Z. Szafrana 4a, 65-516 Zielona Gora, Poland.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Possible consequences of non-exponential behavior of the survival amplitude of an unstable particle at very late times are considered. We describe a new quantum phenomenon: Analyzing the transition time region between exponential and post-exponential form of the survival amplitude we find that the instantaneous energy of the considered unstable state can take large values, much larger than the energy of this state for 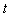 from the exponential time region. We find also that the instantaneous energy of the unstable state tends to the minimal energy of the system
from the exponential time region. We find also that the instantaneous energy of the unstable state tends to the minimal energy of the system 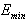 as
as 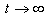 which is much smaller than the energy of this state for
which is much smaller than the energy of this state for 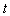 of the order of the lifetime of the considered state. Taking into account the results obtained for the model considered, it is hypothesized that this purely quantum mechanical effect may be responsible for the properties of broad resonances such as
of the order of the lifetime of the considered state. Taking into account the results obtained for the model considered, it is hypothesized that this purely quantum mechanical effect may be responsible for the properties of broad resonances such as 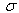 meson as well as having astrophysical consequences.
meson as well as having astrophysical consequences.
Keywords: Non-Exponential Decay, Unstable States
Article Outline
1. Introduction
- Almost all known elementary particles are unstable. So, the knowledge about the properties of unstable particles is one of the fundamental problems in physics. The behavior of unstable states
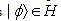 (where
(where 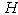 is the Hilbert space of states of the considered system) is characterized by their decay law, which is defined by means of a survival probability amplitude,
is the Hilbert space of states of the considered system) is characterized by their decay law, which is defined by means of a survival probability amplitude, 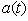 , of finding the system at the time in the initial state
, of finding the system at the time in the initial state 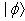 prepared at time
prepared at time 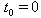 ,
, 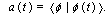 | (1) |
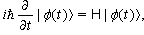 | (2) |
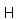 denotes the total selfadjoint Hamiltonian for the system considered.Using the survival amplitude
denotes the total selfadjoint Hamiltonian for the system considered.Using the survival amplitude 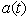 one defines the decay law,
one defines the decay law, 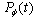 , of an unstable state
, of an unstable state 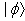 decaying in vacuum as follows
decaying in vacuum as follows 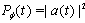 | (3) |
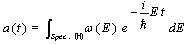 | (4) |
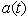 , and thus the decay law
, and thus the decay law 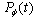 of the unstable state
of the unstable state 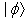 , can be written as the Fourier transform of the density of the energy distribution
, can be written as the Fourier transform of the density of the energy distribution 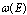 for the system in this state[1, 2] and
for the system in this state[1, 2] and 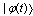 is the solution of the Schrödinger equation for the initial condition
is the solution of the Schrödinger equation for the initial condition 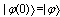 : where
: where 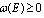 and
and 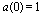 .Khalfin[3] assuming that the spectrum of
.Khalfin[3] assuming that the spectrum of 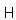 must be bounded from below,
must be bounded from below, 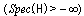 , and using the Paley-Wiener Theorem[4] proved that in the case of unstable states there must be
, and using the Paley-Wiener Theorem[4] proved that in the case of unstable states there must be 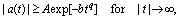 | (5) |
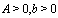 and
and 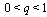 ).In an experiment described in the Rothe paper[5], the experimental evidence of deviations from the exponential decay law at long times was reported. This result gives rise to another problem which now becomes important: If (and how) deviations from the exponential decay law at long times affect the energy of the unstable state and its decay rate at this time region.Note that in fact the amplitude
).In an experiment described in the Rothe paper[5], the experimental evidence of deviations from the exponential decay law at long times was reported. This result gives rise to another problem which now becomes important: If (and how) deviations from the exponential decay law at long times affect the energy of the unstable state and its decay rate at this time region.Note that in fact the amplitude 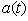 contains information about the decay law
contains information about the decay law 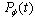 of the state
of the state 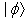 , that is about the decay rate
, that is about the decay rate 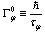 , (
, (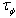 is the lifetime), of this state, as well as the energy
is the lifetime), of this state, as well as the energy 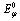 of the system in this state. This information can be extracted from
of the system in this state. This information can be extracted from 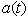 , e. g., using the "effective Hamiltonian"
, e. g., using the "effective Hamiltonian" 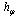 (for details see[6, 7]). In the considered case this
(for details see[6, 7]). In the considered case this 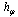 acts in the one-dimensional subspace of states
acts in the one-dimensional subspace of states 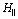 spanned by the normalized vector
spanned by the normalized vector 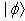 and it is defined as follows (see, eg.[6]),
and it is defined as follows (see, eg.[6]), 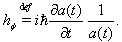 | (6) |
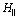 can depend on time
can depend on time 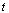 ,
, 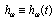 . Within the one pole approximation which is valid to a good approximation for times
. Within the one pole approximation which is valid to a good approximation for times 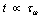 , we have
, we have 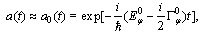 | (7) |
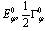 are the pole coordinates, and simply
are the pole coordinates, and simply 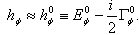 | (8) |
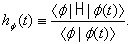 | (9) |
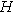 and looks for the rigorous evolution equation for the distinguished subspace of states
and looks for the rigorous evolution equation for the distinguished subspace of states 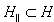 (see[6] and references one finds therein). In the case of one-dimensional
(see[6] and references one finds therein). In the case of one-dimensional 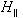 this rigorous Schrödinger-like evolution equation has the following form for the initial condition
this rigorous Schrödinger-like evolution equation has the following form for the initial condition 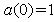 ,[6],
,[6], 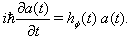 | (10) |
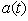 for the state
for the state 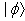 and the exact effective Hamiltonian
and the exact effective Hamiltonian 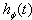 governing the time evolution in the one-dimensional subspace
governing the time evolution in the one-dimensional subspace 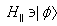 . Thus, the use of the evolution equation (10) or the relation (6) is one of the most effective tools for the accurate analysis of the early- as well as the long-time properties of the energy and decay rate of a given quasi-stationary state
. Thus, the use of the evolution equation (10) or the relation (6) is one of the most effective tools for the accurate analysis of the early- as well as the long-time properties of the energy and decay rate of a given quasi-stationary state 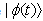 .So let us assume that we know the amplitude
.So let us assume that we know the amplitude 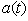 . Then starting with this
. Then starting with this 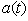 and using the expression (6) one can calculate the effective Hamiltonian
and using the expression (6) one can calculate the effective Hamiltonian 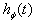 in a general case for every . Thus, one finds the following expressions for the instantaneous energy and the instantaneous decay rate of the system in the state
in a general case for every . Thus, one finds the following expressions for the instantaneous energy and the instantaneous decay rate of the system in the state 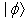 under considerations, (for details see:[7]),
under considerations, (for details see:[7]), 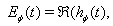 | (11) |
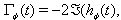 | (12) |
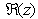 and
and 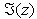 denote the real and imaginary parts of z respectively.Asymptotic long time properties of the instantaneous energy
denote the real and imaginary parts of z respectively.Asymptotic long time properties of the instantaneous energy 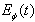 were analyzed in our previous papers for a model of the type considered in Sec. 2 (see[7]) and in a general case[8]). The aim of this paper is to analyze the long time properties of
were analyzed in our previous papers for a model of the type considered in Sec. 2 (see[7]) and in a general case[8]). The aim of this paper is to analyze the long time properties of 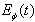 for the transition times region between the exponential and non-exponential form of the survival amplitude using
for the transition times region between the exponential and non-exponential form of the survival amplitude using 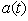 calculated for the given density
calculated for the given density 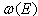 and to discuss possible consequences of these properties.
and to discuss possible consequences of these properties.2. The Model
- Let us assume that
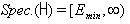 , (where,
, (where, 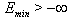 ), and let us choose
), and let us choose 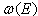 as follows (compare[9])
as follows (compare[9]) 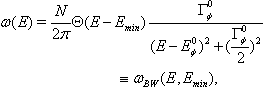 | (13) |
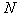 is a normalization constant chosen so that
is a normalization constant chosen so that 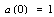 and
and 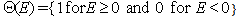 . For such
. For such 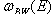 using (4) one finds
using (4) one finds 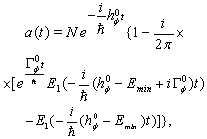 | (14) |
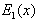 denotes the integral--exponential function[9, 10].In general one has
denotes the integral--exponential function[9, 10].In general one has 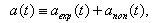 | (15) |
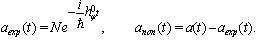 Making use of the asymptotic expansion of
Making use of the asymptotic expansion of 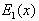 [10]
[10] 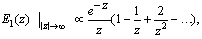 | (16) |
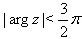 , one concludes that
, one concludes that 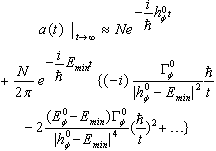 | (17) |
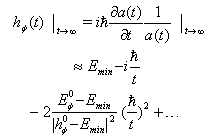 | (18) |
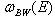 (for details see[7]). From (18) it follows that
(for details see[7]). From (18) it follows that 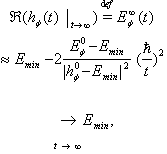 | (19) |
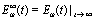 , and
, and 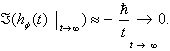 | (20) |
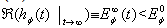 | (21) |
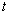 for all densities
for all densities 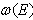 for which the Fourier transform (4) exists. The same can be done for the derivative of
for which the Fourier transform (4) exists. The same can be done for the derivative of 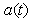 and then using (6) or (9) a general asymptotic form of
and then using (6) or (9) a general asymptotic form of 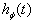 can be found. It looks as follows
can be found. It looks as follows 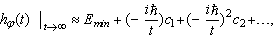 | (22) |
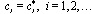 (compare[8]).Note that from (17) one obtains
(compare[8]).Note that from (17) one obtains 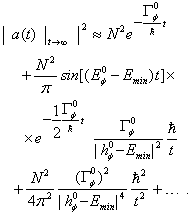 | (23) |
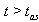 , where
, where 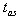 denotes the time
denotes the time 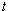 at which contributions to
at which contributions to 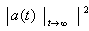 from the first exponential component in (23) and from the third component proportional to 1/t2 are comparable. So
from the first exponential component in (23) and from the third component proportional to 1/t2 are comparable. So 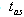 can be be found by considering the following relation Assuming that the right hand side is equal to the left hand side in the above relation one gets a transcendental equation. Exact solutions of such an equation can be expressed by means of the Lambert
can be be found by considering the following relation Assuming that the right hand side is equal to the left hand side in the above relation one gets a transcendental equation. Exact solutions of such an equation can be expressed by means of the Lambert 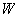 function[11]. An asymptotic solution of the equation obtained from relation (24) is relatively easy to find[12]. The very approximate asymptotic solution,
function[11]. An asymptotic solution of the equation obtained from relation (24) is relatively easy to find[12]. The very approximate asymptotic solution, 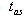 , of this equation for
, of this equation for 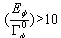 (in general for
(in general for 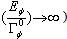 ) has the form
) has the form 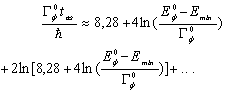 | (25) |
3. Numerical Calculations
- Long time properties of the survival probability
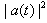 and instantaneous energy
and instantaneous energy 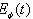 are relatively easy to find analytically for times
are relatively easy to find analytically for times 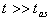 even in the general case as it was shown in[8]. It is much more difficult to analyze these properties analytically in the transition time region where
even in the general case as it was shown in[8]. It is much more difficult to analyze these properties analytically in the transition time region where 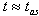 . It can be done numerically for some models (see[13]).The model considered in Sec. 2 and defined by the density
. It can be done numerically for some models (see[13]).The model considered in Sec. 2 and defined by the density 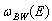 , (13), allows one to find numerically the decay curves and the instantaneous energy
, (13), allows one to find numerically the decay curves and the instantaneous energy 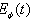 as a function of time
as a function of time 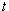 . The results presented in this Section have been obtained assuming for simplicity that the minimal energy
. The results presented in this Section have been obtained assuming for simplicity that the minimal energy 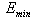 appearing in the formula (13) is equal to zero,
appearing in the formula (13) is equal to zero, 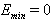 . So, all numerical calculations were performed for the density
. So, all numerical calculations were performed for the density 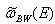 given by the following formula
given by the following formula 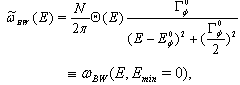 | (26) |
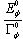 . Performing calculations particular attention was paid to the form of the probability
. Performing calculations particular attention was paid to the form of the probability 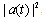 , i. e. of the decay curve, and of the instantaneous energy
, i. e. of the decay curve, and of the instantaneous energy 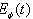 for times
for times 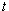 belonging to the most interesting transition time-region between exponential and non-exponential parts of
belonging to the most interesting transition time-region between exponential and non-exponential parts of 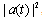 , where the following relation corresponding with (24) takes place,
, where the following relation corresponding with (24) takes place, 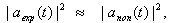 | (27) |
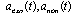 are defined by (15). Results are presented graphically below in Figs (1) - (6).
are defined by (15). Results are presented graphically below in Figs (1) - (6).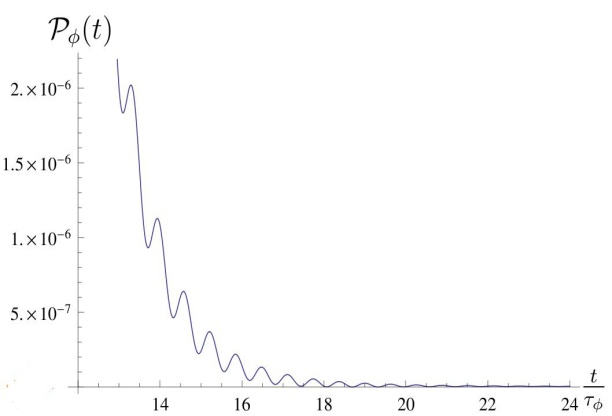 | Figure 1. Survival probability 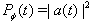 in the transition time region. The case in the transition time region. The case 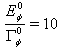 |
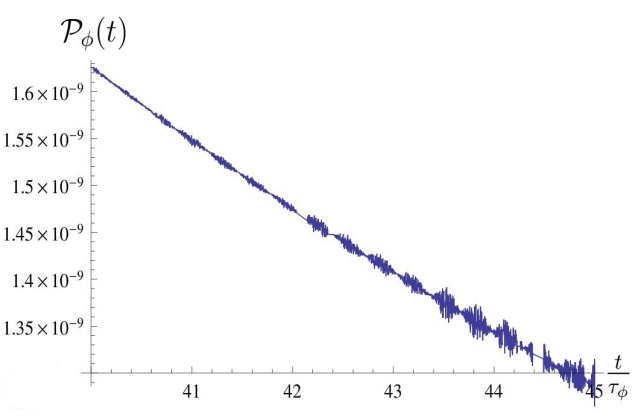 | Figure 2. Survival probability 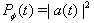 in the transition time region. The case in the transition time region. The case 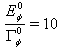 for times t longer than those in Fig. 1 for times t longer than those in Fig. 1 |
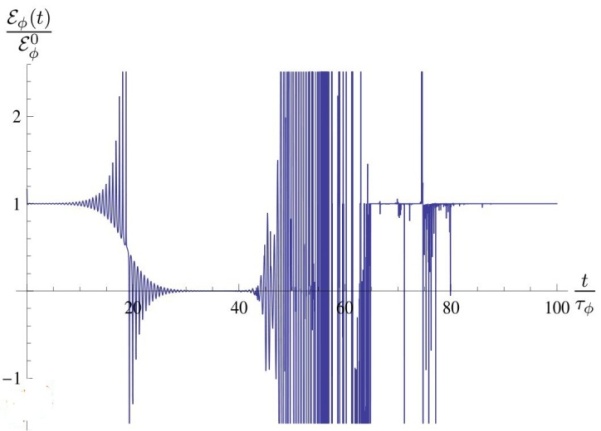 | Figure 3. Instantaneous energy 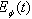 in the transition time region. The case in the transition time region. The case 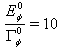 |
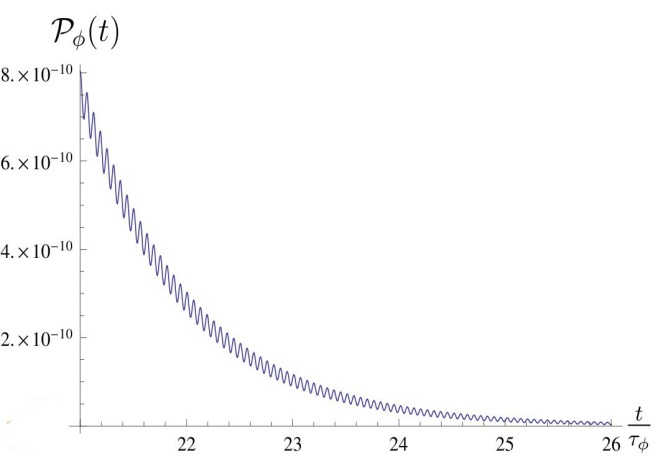 | Figure 4. Survival probability 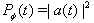 in the transition time region. The case in the transition time region. The case 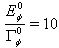 |
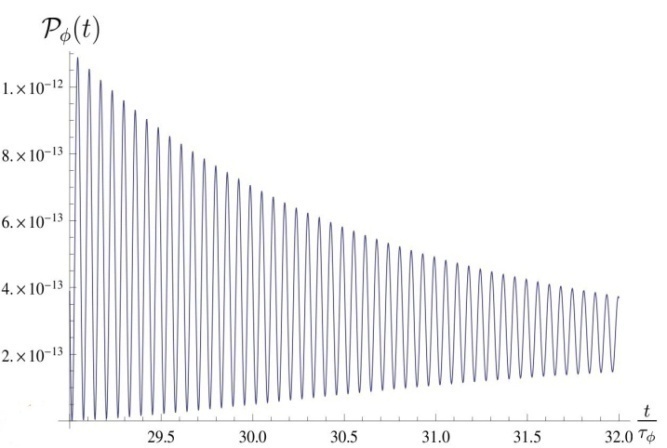 | Figure 5. Survival probability 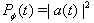 in the transition time region. The case in the transition time region. The case 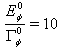 for times t longer than those in Fig. 4 for times t longer than those in Fig. 4 |
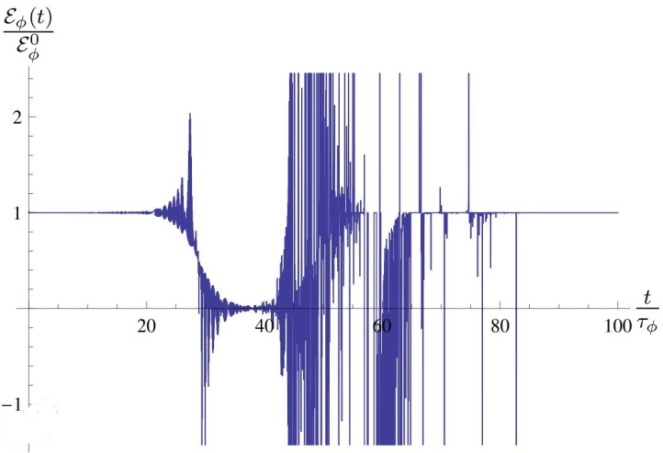 | Figure 6. Instantaneous energy 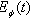 in the transition time region. The case in the transition time region. The case 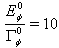 |
4. Discussion: Possible Hyphotetical Effects
- Decay curves of type shown in Fig. (1), Fig. (2), Fig. (4), Fig. (5) can be encountered for a very large class of models defined by energy densities
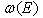 of the following type (see[2, 14]),
of the following type (see[2, 14]), 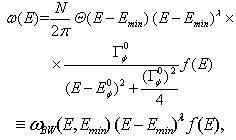 | (28) |
 ,
, 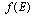 is a form-factor - it is a smooth function going to zero as
is a form-factor - it is a smooth function going to zero as 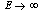 and it has no threshold and no pole. The asymptotical large time behavior of
and it has no threshold and no pole. The asymptotical large time behavior of 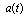 is due to the term
is due to the term 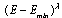 and the choice of
and the choice of 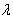 (see, eg.[2, 8]). The Breit-Wigner part,
(see, eg.[2, 8]). The Breit-Wigner part, 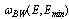 , of the density (28) is responsible for a behavior of
, of the density (28) is responsible for a behavior of 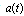 at exponential decay time region and at transition time region. The density
at exponential decay time region and at transition time region. The density 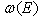 defined by the relation (28) fulfills all physical requirements and it leads to the decay curves of a very similar form at transition times region to the decay curves presented above. The characteristic feature of all these decay curves is the presence of sharp and frequent oscillations at the transition times region (see Figs (1), (2), (4), (5)) (see also, eg.[9],[15] -[20]). So derivatives of the amplitude
defined by the relation (28) fulfills all physical requirements and it leads to the decay curves of a very similar form at transition times region to the decay curves presented above. The characteristic feature of all these decay curves is the presence of sharp and frequent oscillations at the transition times region (see Figs (1), (2), (4), (5)) (see also, eg.[9],[15] -[20]). So derivatives of the amplitude 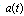 may reach extremely large values for some times from the transition time region and the modulus of these derivatives is much larger than the modulus of
may reach extremely large values for some times from the transition time region and the modulus of these derivatives is much larger than the modulus of 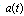 , which is very small for these times. This explains why in this time region the real and imaginary parts of
, which is very small for these times. This explains why in this time region the real and imaginary parts of 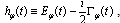 , which can be expressed by the relation (6), ie. by a large derivative of
, which can be expressed by the relation (6), ie. by a large derivative of 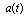 divided by a very small
divided by a very small 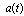 , reach values much larger than the energy
, reach values much larger than the energy 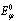 of the unstable state measured at times for which the decay curve has the exponential form. For the model considered we found that, eg. for
of the unstable state measured at times for which the decay curve has the exponential form. For the model considered we found that, eg. for 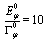 and
and 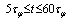 the maximal value of the instantaneous energy equals
the maximal value of the instantaneous energy equals 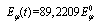 and
and 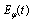 reaches this value for
reaches this value for 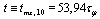 and then the survival probability
and then the survival probability 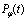 is of order
is of order 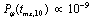 .The question is whether and where this effect can manifest itself. It seems that the following two possibilities of observing the above long time properties of unstable states are worth considering: The first one is that one should analyze the properties of unstable states whose
.The question is whether and where this effect can manifest itself. It seems that the following two possibilities of observing the above long time properties of unstable states are worth considering: The first one is that one should analyze the properties of unstable states whose 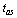 values are not too big. The second one is finding a possibility to observe a suitably large number of events, i.e. unstable particles, created by the same source and living suitably long.The problem with understanding the properties of broad resonances in the scalar sector (
values are not too big. The second one is finding a possibility to observe a suitably large number of events, i.e. unstable particles, created by the same source and living suitably long.The problem with understanding the properties of broad resonances in the scalar sector (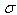 meson problem[21]) discussed in[18,22] and recently in[23] where the hypothesis was formulated that this problem could be connected with the properties of the decay amplitude in the transition time region, seems to be possible manifestations of this effect and this problem refers to the first possibility mentioned above. There is the problem with determining the mass of broad resonances. The measured range of possible mass of the
meson problem[21]) discussed in[18,22] and recently in[23] where the hypothesis was formulated that this problem could be connected with the properties of the decay amplitude in the transition time region, seems to be possible manifestations of this effect and this problem refers to the first possibility mentioned above. There is the problem with determining the mass of broad resonances. The measured range of possible mass of the 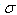 meson is very wide, 400 - 1200 MeV. So one can not exclude the possibility that the masses of some
meson is very wide, 400 - 1200 MeV. So one can not exclude the possibility that the masses of some 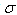 mesons are measured for times of the order of their lifetime and some of them for times where their instantaneous energy
mesons are measured for times of the order of their lifetime and some of them for times where their instantaneous energy 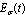 is much larger. This is exactly the case presented in Fig. (3) and Fig. (6). For broad mesons the ratio
is much larger. This is exactly the case presented in Fig. (3) and Fig. (6). For broad mesons the ratio 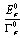 is relatively small and thus the time
is relatively small and thus the time 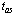 , when the above discussed effect occurs, appears to be not too long.Astrophysical and cosmological processes in which extremely huge numbers of unstable particles are created seem to be another possibility for the above discussed effect to become manifest. Rapid fluctuations of the instantaneous energy
, when the above discussed effect occurs, appears to be not too long.Astrophysical and cosmological processes in which extremely huge numbers of unstable particles are created seem to be another possibility for the above discussed effect to become manifest. Rapid fluctuations of the instantaneous energy 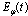 (see Figs 3 and 6) of unstable particles
(see Figs 3 and 6) of unstable particles 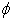 take place at times
take place at times 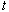 of order
of order 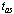 . Fluctuations of
. Fluctuations of 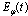 lead to fluctuations of instantaneous masses,
lead to fluctuations of instantaneous masses, 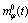 , of particles
, of particles 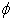 ,
, 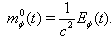 | (29) |
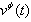 close to the speed of light c. The energy
close to the speed of light c. The energy 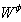 of such moving particles,
of such moving particles, 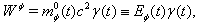 | (30) |
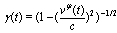 , should be the same at times
, should be the same at times 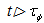 and at times
and at times 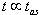 . This follows from the principle of the energy conservation. From relation (30) one can infer that this is possible only when changes of
. This follows from the principle of the energy conservation. From relation (30) one can infer that this is possible only when changes of 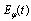 at times
at times 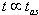 are balanced with suitable changes of
are balanced with suitable changes of 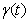 (i.e. of the velocity
(i.e. of the velocity 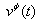 ). So, in the case of moving unstable particles, rapid fluctuations (changes) of their velocities should be observed at distances
). So, in the case of moving unstable particles, rapid fluctuations (changes) of their velocities should be observed at distances 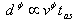 from their source. It seems to be obvious that astrophysical and cosmological processes are the only sources able to create suitably large number of unstable particles guaranteeing that a part of them survives up to times
from their source. It seems to be obvious that astrophysical and cosmological processes are the only sources able to create suitably large number of unstable particles guaranteeing that a part of them survives up to times 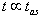 . Therefore an analysis of these processes and observational data connected with them seems to be only chance to find possible effects caused by rapid fluctuations of velocities of unstable particles at late times.It appears that properties of unstable states at times t much later than
. Therefore an analysis of these processes and observational data connected with them seems to be only chance to find possible effects caused by rapid fluctuations of velocities of unstable particles at late times.It appears that properties of unstable states at times t much later than 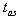 described by the decay law (23) and relations (18), (19) and (22) may be useful when one tries to explain some cosmological processes. The late time behavior of false vacuum decay is an example of such processes[24, 25, 26]. The false vacuum[24,25] is metastable and space areas with false vacuum decay by tunneling to the space area with the true vacuum state. Some space areas with false vacuum can survive up o times
described by the decay law (23) and relations (18), (19) and (22) may be useful when one tries to explain some cosmological processes. The late time behavior of false vacuum decay is an example of such processes[24, 25, 26]. The false vacuum[24,25] is metastable and space areas with false vacuum decay by tunneling to the space area with the true vacuum state. Some space areas with false vacuum can survive up o times 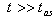 and then properties of these false vacuum states are described by relations (18), (19) and (22)[26]. At times
and then properties of these false vacuum states are described by relations (18), (19) and (22)[26]. At times 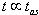 the energy of the false vacuum state should fluctuate very fast according to the results presented in Fig. 3 na 6. This may also affect properties and a behavior of space bubbles with false vacua.Note that all possible effects discussed in this paper are the simple consequence of the fact that the instantaneous energy
the energy of the false vacuum state should fluctuate very fast according to the results presented in Fig. 3 na 6. This may also affect properties and a behavior of space bubbles with false vacua.Note that all possible effects discussed in this paper are the simple consequence of the fact that the instantaneous energy 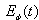 of unstable particles becomes large for suitably long times compared with
of unstable particles becomes large for suitably long times compared with 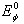 and for some times even extremely large. This property of
and for some times even extremely large. This property of 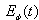 is a purely quantum effect resulting from the assumption that the energy spectrum is bounded from below and it was found by performing a rigorous analysis of the properties of the quantum mechanical survival probability
is a purely quantum effect resulting from the assumption that the energy spectrum is bounded from below and it was found by performing a rigorous analysis of the properties of the quantum mechanical survival probability 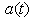 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML