-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2012; 2(3): 57-70
doi:10.5923/j.jnpp.20120203.05
On the Photonuclear Rates Calculation for Nuclear Transmutation of Beta Decay Nuclides by Application of the Ginzburg-landau Theory
Stefan Mehedinteanu
CITON – Center of Technology and Engineering for Nuclear Projects, Str. Atomistilor No. 409, BOP-5204-MG-4, Oras Magurele, Ilfov, Romania
Correspondence to: Stefan Mehedinteanu, CITON – Center of Technology and Engineering for Nuclear Projects, Str. Atomistilor No. 409, BOP-5204-MG-4, Oras Magurele, Ilfov, Romania.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
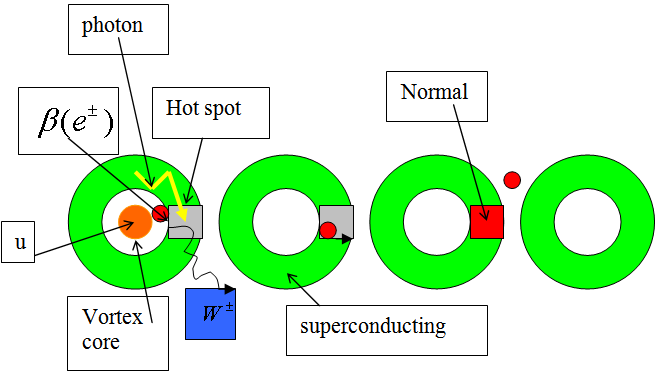
The main aim of this paper is to found which are the conditions the photonuclear reactions in order to accelerate the beta decay of radionuclides. Therefore, it was developed a new model where the photonuclear reaction at above the giant resonance cross section (GR) is viewed as an incident photon creating superconducting hot spot (hot belt) across nucleons from a neutron-proton[n-p] pair (a quasi-deuteron ) of the valence bosons of a unstable nuclide, accordingly with IBAF model and, followed by a thermally induced vortex crossing, which turns superconducting hot belt into the normal state (vacuum) resulting in a vortex assisted photon beta decay with the fermion (e+,e-) release (capture), and eventually the pair break-up by a reaction 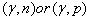 . Since, a such model requires data on energies of vortex and on currents from inside of the nucleon, an analogue of a superconductor model was developed for the nucleon, and tested on the data of natural beta decay viewed as dark count. The results consist in obtaining a precise value of the threshold energy of the photons when the beta decay of the radionuclides is accelerated. Such efficient installations could be , for example, the laser ELI-NP in construction in Romania for the higher energy photons source.
. Since, a such model requires data on energies of vortex and on currents from inside of the nucleon, an analogue of a superconductor model was developed for the nucleon, and tested on the data of natural beta decay viewed as dark count. The results consist in obtaining a precise value of the threshold energy of the photons when the beta decay of the radionuclides is accelerated. Such efficient installations could be , for example, the laser ELI-NP in construction in Romania for the higher energy photons source.
Keywords: Beta Decay, Nuclear Transmutation, Photonuclear Reactions, High Energy Lasers, W,Z, Higgs Bosons, G-L Theory
Cite this paper: Stefan Mehedinteanu, On the Photonuclear Rates Calculation for Nuclear Transmutation of Beta Decay Nuclides by Application of the Ginzburg-landau Theory, Journal of Nuclear and Particle Physics, Vol. 2 No. 3, 2012, pp. 57-70. doi: 10.5923/j.jnpp.20120203.05.
Article Outline
1. Introduction
- Photonuclear reactions are proven to be of potential interest for nuclear transmutation[1] in the handling of radioactive waste, which is a big problem in nuclear energy.Photonuclear cross sections are quite large at the giant resonance(GR) region of
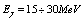 . Major
. Major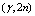 and
and 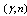 reactions on long-lived nuclei may transmute them to short-lived of beta decay type or stable nuclei.Coherent photonuclear isotope transmutation (CPIT) produces exclusively radioactive isotopes (RIs) by coherent photonuclear
reactions on long-lived nuclei may transmute them to short-lived of beta decay type or stable nuclei.Coherent photonuclear isotope transmutation (CPIT) produces exclusively radioactive isotopes (RIs) by coherent photonuclear 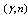 and
and 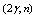 reactions via E1 giant resonances[1]. Photons to be used are medium energy
reactions via E1 giant resonances[1]. Photons to be used are medium energy 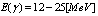 photons produced by laser photons backscattered off
photons produced by laser photons backscattered off 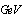 electrons.The photon intensity of around
electrons.The photon intensity of around 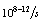 is realistic by using intense lasers and intense electrons. In future high intensity photon sources with the intensity of the order of
is realistic by using intense lasers and intense electrons. In future high intensity photon sources with the intensity of the order of 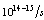 will be possible. Therefore, are two conditions for aphotonuclear reaction the intensity, and the threshold energy. For example, intense electron accelerators provide bremestrahlung photons for photonuclear isotope transmutation but most of photons are below the threshold energy of the photonuclear reaction.Otherwise, in[2a] is argued that photon counts in a superconducting nanowire single-photon detector (SNSPD) are caused by the transition from a current-biased metastable superconducting(s) state to the normal (n) state. Such a transition is triggered by vortices crossing the thin film superconducting strip from one edge to another due to the Lorentz force. Hence, the general picture is that the vortex crossing may trigger the
will be possible. Therefore, are two conditions for aphotonuclear reaction the intensity, and the threshold energy. For example, intense electron accelerators provide bremestrahlung photons for photonuclear isotope transmutation but most of photons are below the threshold energy of the photonuclear reaction.Otherwise, in[2a] is argued that photon counts in a superconducting nanowire single-photon detector (SNSPD) are caused by the transition from a current-biased metastable superconducting(s) state to the normal (n) state. Such a transition is triggered by vortices crossing the thin film superconducting strip from one edge to another due to the Lorentz force. Hence, the general picture is that the vortex crossing may trigger the 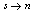 transition. A photon makes this process much more probable by creating a spot with suppressed order parameter and thus with lower energy barrier for vortex crossing. The model developed in[2a] is based entirely on the Ginsburg-Landau theory of superconductivity.In the present paper-section 3, based on the above models[1],[2a], a new model is introduced, respectively, a photonuclear reaction at above the (GR) viewed as an incident photon creating superconducting hot spot (hot belt) across a nucleon from a neutron-proton[n-p] pair (a quasi-deuteron as was baptized by Levinger[36]) of the valence bosons of a unstable nuclide, accordingly with IBA model[25],[31] and, followed by a thermally induced vortex crossing, which turns superconducting hot belt into the normal state (vacuum) resulting in a vortex assisted photon beta decay with the fermion (e+,e-) release (capture)[25], and eventually the pair break-up by a reaction
transition. A photon makes this process much more probable by creating a spot with suppressed order parameter and thus with lower energy barrier for vortex crossing. The model developed in[2a] is based entirely on the Ginsburg-Landau theory of superconductivity.In the present paper-section 3, based on the above models[1],[2a], a new model is introduced, respectively, a photonuclear reaction at above the (GR) viewed as an incident photon creating superconducting hot spot (hot belt) across a nucleon from a neutron-proton[n-p] pair (a quasi-deuteron as was baptized by Levinger[36]) of the valence bosons of a unstable nuclide, accordingly with IBA model[25],[31] and, followed by a thermally induced vortex crossing, which turns superconducting hot belt into the normal state (vacuum) resulting in a vortex assisted photon beta decay with the fermion (e+,e-) release (capture)[25], and eventually the pair break-up by a reaction 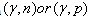 . The first mention in literature of the connection between the photonuclear reaction and superconducting it was when the characteristic feature of thermalized non-equilibrated matter is that, in spite of energy relaxation–equilibration, a phase memory of the way the many-body system was excited remains[37]. There, in order to demonstrate that, it is analysed the proton yield of the
. The first mention in literature of the connection between the photonuclear reaction and superconducting it was when the characteristic feature of thermalized non-equilibrated matter is that, in spite of energy relaxation–equilibration, a phase memory of the way the many-body system was excited remains[37]. There, in order to demonstrate that, it is analysed the proton yield of the 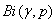 photonuclear reaction produced by 24 MeV bremsstrahlung, when the properly scaled angle-integrated spectrum for the outgoing proton energy
photonuclear reaction produced by 24 MeV bremsstrahlung, when the properly scaled angle-integrated spectrum for the outgoing proton energy 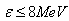 has an exponential shape with a slope of 0.55 MeV. This is characteristic for the decay of thermalized compound nucleus with a “temperature” T = 0.55 MeV (or 6.3109K) of the residual nucleus. The average excitation energy of the compound nucleus was evaluated at E*= 14 MeV, i.e. slightly above the center of the dipole giant resonance peak at 13.5 MeV. The characteristic time for the formation of such thermalized many-body states is given by the inverse spreading width,
has an exponential shape with a slope of 0.55 MeV. This is characteristic for the decay of thermalized compound nucleus with a “temperature” T = 0.55 MeV (or 6.3109K) of the residual nucleus. The average excitation energy of the compound nucleus was evaluated at E*= 14 MeV, i.e. slightly above the center of the dipole giant resonance peak at 13.5 MeV. The characteristic time for the formation of such thermalized many-body states is given by the inverse spreading width,  , where
, where 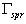 is the width of a dipole giant resonance, which is about 4.5 MeV for Bi. Notice that
is the width of a dipole giant resonance, which is about 4.5 MeV for Bi. Notice that 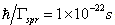 is the energy relaxation time and
is the energy relaxation time and 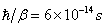 is phase memory time or phase relaxation time, and phase relaxation width
is phase memory time or phase relaxation time, and phase relaxation width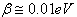 . Therefore, the phase relaxation is at least 8 orders of magnitude slower than energy relaxation. This argues that thermalized non-equilibrated matter resembles a high temperature superconducting state in quantum many-body systems.Since, this model requires data on energies of vortex and on currents from inside of the nucleon, an analogue of a superconductor model was developed for the nucleon[37], and described in section 2.In section 4 is applied this model to the mechanism of natural beta decay viewed as dark count.The results consist in obtaining a precise value of the threshold energy of the photons when the beta decay of the radionuclides is accelerated. If these kind of predictions continue to be verified by appropriate experiments, one may have a cheap solution to remove the radioactive waste of used-up nuclear fuel rods of fission reactors in a time period of a few years.
. Therefore, the phase relaxation is at least 8 orders of magnitude slower than energy relaxation. This argues that thermalized non-equilibrated matter resembles a high temperature superconducting state in quantum many-body systems.Since, this model requires data on energies of vortex and on currents from inside of the nucleon, an analogue of a superconductor model was developed for the nucleon[37], and described in section 2.In section 4 is applied this model to the mechanism of natural beta decay viewed as dark count.The results consist in obtaining a precise value of the threshold energy of the photons when the beta decay of the radionuclides is accelerated. If these kind of predictions continue to be verified by appropriate experiments, one may have a cheap solution to remove the radioactive waste of used-up nuclear fuel rods of fission reactors in a time period of a few years.2. The Description of the Analogue Model of Nucleon to a Superconductor
- Usually, the masses of
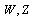 , are calculated by taking into account an a-priori a Higgs field, and the default using the Higgs mechanism and Higgs boson.Soon after the advent of QCD, ’t Hooft and Mandelstam[3] proposed the dual superconductor scenario of confinement; the QCD vacuum is thought to behave analogously to an electrodynamic superconductor but with the roles of electric and magnetic fields being interchanged: a condensate of magnetic monopoles expels electric fields from the vacuum. If one now puts electric charge and anti-charge into this medium, the electric flux that forms between them will be squeezed into a thin, eventually string-like, Abrikosov-Nielsen-Oleson (ANO) vortex which results in linear confinement.The dual superconductor mechanism[3] is an alternative that does not require the ad hoc introduction of a Higgs field but instead uses dynamically generated topological excitations to provide the screening supercurrents. For example, U(1) lattice gauge theory contains Dirac magnetic monopoles in addition to photons. The dual superconductor hypothesis postulates that these monopoles provide the circulating color magnetic currents that constrain the color electric flux lines into narrow flux tubes. ’t Hooft has shown that objects similar to the Dirac monopoles in U(1) gauge theory can also be found in non-Abelian SU(N) models.The results are consistent with a dual version of the Ginzburg-Landau model of superconductivity. Important in understanding field (magnetic) dependence was Abrikosov’s field theoretical approaches based on Ginsburg-Landau theory[4] for type I superconductors (
, are calculated by taking into account an a-priori a Higgs field, and the default using the Higgs mechanism and Higgs boson.Soon after the advent of QCD, ’t Hooft and Mandelstam[3] proposed the dual superconductor scenario of confinement; the QCD vacuum is thought to behave analogously to an electrodynamic superconductor but with the roles of electric and magnetic fields being interchanged: a condensate of magnetic monopoles expels electric fields from the vacuum. If one now puts electric charge and anti-charge into this medium, the electric flux that forms between them will be squeezed into a thin, eventually string-like, Abrikosov-Nielsen-Oleson (ANO) vortex which results in linear confinement.The dual superconductor mechanism[3] is an alternative that does not require the ad hoc introduction of a Higgs field but instead uses dynamically generated topological excitations to provide the screening supercurrents. For example, U(1) lattice gauge theory contains Dirac magnetic monopoles in addition to photons. The dual superconductor hypothesis postulates that these monopoles provide the circulating color magnetic currents that constrain the color electric flux lines into narrow flux tubes. ’t Hooft has shown that objects similar to the Dirac monopoles in U(1) gauge theory can also be found in non-Abelian SU(N) models.The results are consistent with a dual version of the Ginzburg-Landau model of superconductivity. Important in understanding field (magnetic) dependence was Abrikosov’s field theoretical approaches based on Ginsburg-Landau theory[4] for type I superconductors (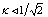 ,
, 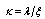 ,
, 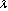 is the penetration depth,
is the penetration depth, 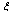 the coherence length ) and type ones (
the coherence length ) and type ones (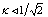 ) II superconductors, which allows magnetic flux
) II superconductors, which allows magnetic flux 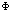 to penetrate the superconductor in a regular array quantized in units of elementary flux quantum
to penetrate the superconductor in a regular array quantized in units of elementary flux quantum  . Important was the quantization in a ring , flux
. Important was the quantization in a ring , flux 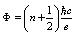 , (
, (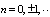 )Accordingly, we revisited G-L model[4-13] in order to calculate the values of the Lorenz force, the current, and the energies of the Abrikosov vortex lines inside of the nucleon, in natural units, firstly, in view to search for its relevance; for the time being, it was found that this would correspond to energies for subatomic particles, such as that of
)Accordingly, we revisited G-L model[4-13] in order to calculate the values of the Lorenz force, the current, and the energies of the Abrikosov vortex lines inside of the nucleon, in natural units, firstly, in view to search for its relevance; for the time being, it was found that this would correspond to energies for subatomic particles, such as that of 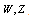 , bosons, and of pion
, bosons, and of pion 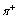 , and secondarily to be used in the model of vortex-assisted single photon count. In this model to a superconductor analogue, we do not use any a- priori field (Higgs) and hence a Higgs boson, we use only a comparison with the electrical field generated by the pair (dipole)
, and secondarily to be used in the model of vortex-assisted single photon count. In this model to a superconductor analogue, we do not use any a- priori field (Higgs) and hence a Higgs boson, we use only a comparison with the electrical field generated by the pair (dipole) 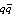 .It is known, that the normal cores that exist in type-II superconductors in the mixed state are not sharply delineated. The value of number density of superelectrons
.It is known, that the normal cores that exist in type-II superconductors in the mixed state are not sharply delineated. The value of number density of superelectrons 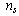 is zero at the centers of the cores and rises over a characteristic distance
is zero at the centers of the cores and rises over a characteristic distance 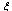 , the coherence length. The magnetic field associated with each normal core is spread over a region with a diameter of
, the coherence length. The magnetic field associated with each normal core is spread over a region with a diameter of 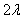 , and each normal core is surrounded by a vortex of circulating current. The QCD vacuum can be viewed as a dual superconductor characterized by a monopole condensate[3,9,11], when embedding a static
, and each normal core is surrounded by a vortex of circulating current. The QCD vacuum can be viewed as a dual superconductor characterized by a monopole condensate[3,9,11], when embedding a static 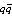 pair into the vacuum. The core of the flux tube is just a normal conducting vortex which is stabilized by solenoidal magnetic supercurrents,
pair into the vacuum. The core of the flux tube is just a normal conducting vortex which is stabilized by solenoidal magnetic supercurrents, 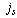 , in the surrounding vacuum. In order to calculate distinctly the energy states (masses) in natural units, firstly we re-derive the field equations of magnetic monopoles current, of the electric flux and energy states.Therefore, here is adopted a basic dual (
, in the surrounding vacuum. In order to calculate distinctly the energy states (masses) in natural units, firstly we re-derive the field equations of magnetic monopoles current, of the electric flux and energy states.Therefore, here is adopted a basic dual (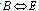 ) form of Ginzburg-Landau (G-L) theory[4-8], which generalizes the London theory to allow the magnitude of the condensate density to vary in space. As before, the superconducting order parameter is a complex function
) form of Ginzburg-Landau (G-L) theory[4-8], which generalizes the London theory to allow the magnitude of the condensate density to vary in space. As before, the superconducting order parameter is a complex function 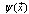 , where
, where 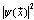 is the condensate density
is the condensate density 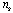 . Also is defined the wave function
. Also is defined the wave function 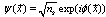 , where
, where 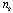 is the London (bulk) condensate density, and
is the London (bulk) condensate density, and 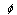 are real functions describing the spatial variation of the condensate.The characteristic scale over which the condensate density varies is
are real functions describing the spatial variation of the condensate.The characteristic scale over which the condensate density varies is 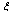 , the G-L coherence length or the vortex core dimension . The x denote the radial distance of points from the
, the G-L coherence length or the vortex core dimension . The x denote the radial distance of points from the 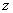 -axis, the superconductor occupying the half space
-axis, the superconductor occupying the half space 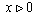 . Outside of the superconductor in the half space
. Outside of the superconductor in the half space 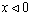 , one has
, one has 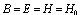 , where, “the external” vector
, where, “the external” vector 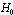 is parallel to the surface. The
is parallel to the surface. The 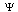 theory of superconductivity[3,4] is an application of the Landau theory of phase transitions to superconductivity. In this case, some scalar complex
theory of superconductivity[3,4] is an application of the Landau theory of phase transitions to superconductivity. In this case, some scalar complex 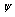 function fulfils the role of the order parameter. The final expression for the free energy then takes the form
function fulfils the role of the order parameter. The final expression for the free energy then takes the form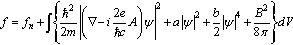 | (1) |
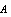 and
and 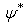 . Carrying first variation with respect to
. Carrying first variation with respect to 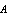 , we find after a simple calculation:
, we find after a simple calculation: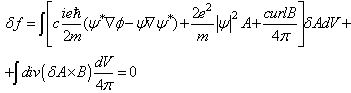 | (2) |
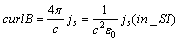 | (3) |
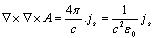 | (4) |
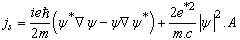 | (5) |
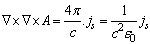 | (6) |
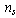 we use
we use 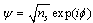 . The second integral is over the surface of the sample. The volume integral vanishes when
. The second integral is over the surface of the sample. The volume integral vanishes when 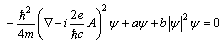 | (7) |
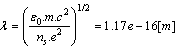 , and the quantized flux:
, and the quantized flux: 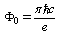 , and
, and 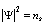 ;
; 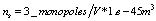 ,
, 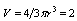 ,
, 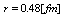
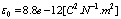 . Since, the magnetic charge of monopole being[17]
. Since, the magnetic charge of monopole being[17] 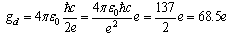 , and assuming that the classical electron radius be equal to “the classical monopole radius” from which one has the monopole mass
, and assuming that the classical electron radius be equal to “the classical monopole radius” from which one has the monopole mass 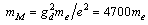 , the value of
, the value of 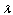 remains unmodified.The superconductors of second kind are those with
remains unmodified.The superconductors of second kind are those with 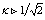 , and
, and 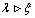 .We now consider the phase transition in superconductors of the second kind. For this we can omit the non-linear
.We now consider the phase transition in superconductors of the second kind. For this we can omit the non-linear 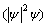 term in (7), we have
term in (7), we have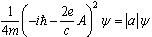 | (8) |
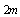 and charge
and charge 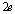 (in the case of dual, the factor 2 for the charge, which is specific to the “pairs”, it is actually 1) in a magnetic field
(in the case of dual, the factor 2 for the charge, which is specific to the “pairs”, it is actually 1) in a magnetic field 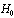 (in our case the chromo-electrical flux
(in our case the chromo-electrical flux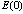 ). The quantity
). The quantity 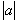 plays the role of energy (
plays the role of energy ( ) of that equation. The minimum energy for a such particle in a uniform electro-magnetic field is
) of that equation. The minimum energy for a such particle in a uniform electro-magnetic field is 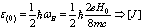 ,
, 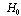 -an “external” electro-magnetic field of a dipole created by the pair
-an “external” electro-magnetic field of a dipole created by the pair 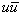 (the chromoelectrical colors field)
(the chromoelectrical colors field)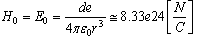 | (9) |
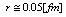 -is the electrical flux tube radius,
-is the electrical flux tube radius, 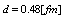 -the distance between the two quarks charges, usually
-the distance between the two quarks charges, usually 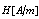 , but here is used as
, but here is used as 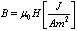 Hence, equation (8) has a solution only if
Hence, equation (8) has a solution only if 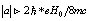 , when following power-law conformal map is applied for complex number of the r.h.s of (8), or equivalently if the electro-magnetic field is less than an upper critical field, see fig.1a
, when following power-law conformal map is applied for complex number of the r.h.s of (8), or equivalently if the electro-magnetic field is less than an upper critical field, see fig.1a 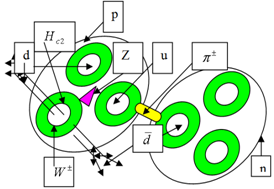 | Figure 1a. Abrikosov’s triangular lattice for a nucleon (proposal) |
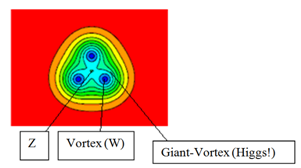 | Figure 1b. The Giant-Vortex (after Ref.[24]) type arrangement for the nucleon (only illustration) |
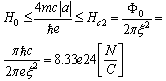 | (10) |
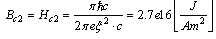 The particle energy is
The particle energy is 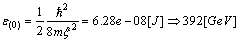 with
with 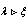 ;
; 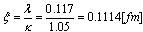 , or
, or 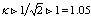 (of type II-superconductor). One of the characteristic lengths for the description of superconductors is called the coherence length. For example, a transition from the superconducting state to a normal state will have a transition layer of finite thickness which is related to the coherence length.More exactly, this quantity is called the correlation or healing length[4] , and is defined as
(of type II-superconductor). One of the characteristic lengths for the description of superconductors is called the coherence length. For example, a transition from the superconducting state to a normal state will have a transition layer of finite thickness which is related to the coherence length.More exactly, this quantity is called the correlation or healing length[4] , and is defined as 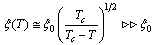 where
where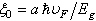 | (11) |
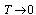 ,
,  from[19],
from[19], 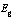 -gap energy,
-gap energy, 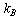 Boltzmann constant; at confinement
Boltzmann constant; at confinement 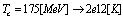 , and the Fermi velocity of electrons (monopoles) is
, and the Fermi velocity of electrons (monopoles) is  | (12) |
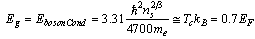 where
where 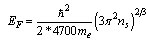 | (13) |
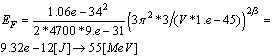 where
where 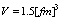 , and the velocity of monopole is
, and the velocity of monopole is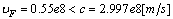 and
and 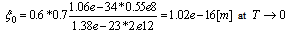 | (14) |
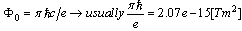 | (15) |
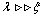 (near
(near 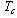 this means
this means 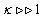 ). Thus, when the electrical flux is applied parallel to the superconducting cylinder, the first flux penetrating should be located along the axis of the cylinder.In the range
). Thus, when the electrical flux is applied parallel to the superconducting cylinder, the first flux penetrating should be located along the axis of the cylinder.In the range 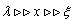 | (16) |
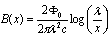 | (17) |
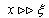 | (18) |
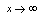 is
is 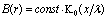 , where
, where 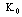 is the Hankel function of imaginary argument. The coefficient must be defined by matching with the solution of (17). Using the asymptotic formula
is the Hankel function of imaginary argument. The coefficient must be defined by matching with the solution of (17). Using the asymptotic formula 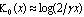 for
for 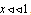 ,where
,where 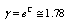 (C is Euler’s constant), we finally have
(C is Euler’s constant), we finally have 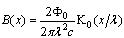 | (19) |
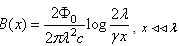 | (19.1) |
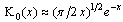 for
for 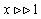 . Thus, at large distances from the axis of the vortex line the field decreases according to
. Thus, at large distances from the axis of the vortex line the field decreases according to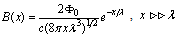 | (20) |
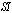 ):
):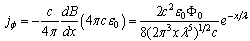 | (21) |
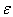 of the vortex line, we obtain for the energy per unit length of vortex line.
of the vortex line, we obtain for the energy per unit length of vortex line. 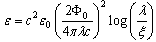 | (22) |
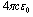 is used to convert from
is used to convert from 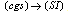 .Because the magnetic induction of the monopoles current which is powered by electric field given by a pair of quarks (
.Because the magnetic induction of the monopoles current which is powered by electric field given by a pair of quarks (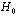 ), it has the raw flow consequences squeezing this cromoelectrical flux into a vortex line, followed by forcing an organization into a triangular Abrikosov lattice, see figure 1.The core of every vortex can be considered to contain a vortex line, and every particle in the vortex can be considered to be circulating around the vortex line. Vortex lines can start and end at the boundary of the fluid or form closed loops.The presence of vortex line which increases the free energy of the superconducting media with
), it has the raw flow consequences squeezing this cromoelectrical flux into a vortex line, followed by forcing an organization into a triangular Abrikosov lattice, see figure 1.The core of every vortex can be considered to contain a vortex line, and every particle in the vortex can be considered to be circulating around the vortex line. Vortex lines can start and end at the boundary of the fluid or form closed loops.The presence of vortex line which increases the free energy of the superconducting media with 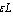 , it is thermodynamically favorable if the contribution is negative; i.e. if
, it is thermodynamically favorable if the contribution is negative; i.e. if 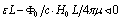 , and
, and 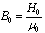 ,
, 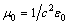 , or
, or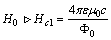 | (23) |
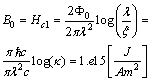 | (24) |
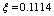 , and when near the axis, for
, and when near the axis, for 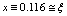 from (20) when the induction is
from (20) when the induction is 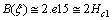 | (25) |
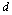 from each other.
from each other. 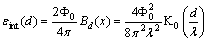 | (26) |
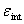 (see eq. (20))
(see eq. (20))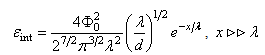 | (27) |
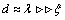 the cores of vortex lines overlap[4]. Let us consider a closed contour near the surface of the cylinder. The change of wave function on passing round the contour is
the cores of vortex lines overlap[4]. Let us consider a closed contour near the surface of the cylinder. The change of wave function on passing round the contour is 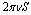 , where
, where 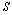 is the cross-section area of the cylinder and
is the cross-section area of the cylinder and 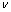 -the number of vortex lines. The electric flux is
-the number of vortex lines. The electric flux is 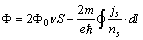 | (28) |
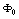 , and is surrounded by a circulating suppercurrent,
, and is surrounded by a circulating suppercurrent, 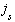 , of spatial extent,
, of spatial extent, 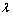 . As the applied field increases, the fluxoids begin to interact and as the consequence ensembles themselves into a lattice. A simple geometrical argument for the spacing,
. As the applied field increases, the fluxoids begin to interact and as the consequence ensembles themselves into a lattice. A simple geometrical argument for the spacing, 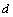 of a triangular lattice then gives the flux quantization condition[13],
of a triangular lattice then gives the flux quantization condition[13], 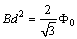 | (29) |
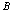 , is the induction.The solution of Ginzburg-Landau phenomenological free energy (13) is useful for understanding the Abrikosov flux lattice. The coordinate-dependent order parameter
, is the induction.The solution of Ginzburg-Landau phenomenological free energy (13) is useful for understanding the Abrikosov flux lattice. The coordinate-dependent order parameter 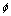 describes the flux vortices of periodicity of a triangular lattice. Fluctuations from
describes the flux vortices of periodicity of a triangular lattice. Fluctuations from 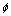 change the state to
change the state to 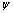 , the minimization of free energy with respect to
, the minimization of free energy with respect to 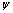 , gives the ground state
, gives the ground state 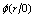 .The free energy is given by,
.The free energy is given by, 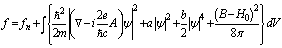 | (30) |
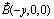 . The free energy has solutions of vortices of triangular form. The coordinates of the three vertices of a triangular vortex are given by
. The free energy has solutions of vortices of triangular form. The coordinates of the three vertices of a triangular vortex are given by 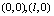 , and
, and 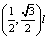 . The fluctuation from ground state corresponding to that of triangular lattice is that for small fluctuations. The deviation of the free energy from the mean-field value
. The fluctuation from ground state corresponding to that of triangular lattice is that for small fluctuations. The deviation of the free energy from the mean-field value 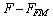 with respect to the thermal energy,
with respect to the thermal energy, 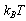 , can be used to obtain the physical properties of the fluctuations which are useful for understanding the melted vortex lattices. The deviation from the triangular Abrikosov lattice is defined as
, can be used to obtain the physical properties of the fluctuations which are useful for understanding the melted vortex lattices. The deviation from the triangular Abrikosov lattice is defined as 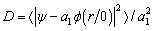 | (31) |
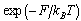 . Classically,
. Classically, 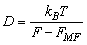 | (32) |
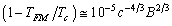 | (33) |
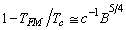 | (34) |
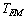 -the flux-lattice melting temperature, and
-the flux-lattice melting temperature, and 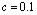 from Lindemann criterion of lattice melting when
from Lindemann criterion of lattice melting when 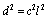 , the flux quantization condition
, the flux quantization condition 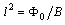 ,
, 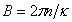 , where
, where 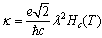 , and
, and 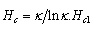 .For numerical values
.For numerical values 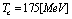 , in case of symmetry breaking, in case 1, results
, in case of symmetry breaking, in case 1, results 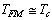 , and in case 2, results
, and in case 2, results 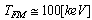 by using (29) in place of
by using (29) in place of 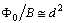 with
with 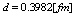 (a very precisely value), and
(a very precisely value), and 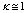 , which is the temperature of fusion (melting!) of two protons.This triangular lattice corresponds to the arrangement of the quarks pairs
, which is the temperature of fusion (melting!) of two protons.This triangular lattice corresponds to the arrangement of the quarks pairs 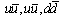 in the frame of a nucleon, see fig.1a; fig.1b.A direct numerical analysis allows to obtain the following values for the current, force and energy. Thus, from (21) the current is given by:
in the frame of a nucleon, see fig.1a; fig.1b.A direct numerical analysis allows to obtain the following values for the current, force and energy. Thus, from (21) the current is given by: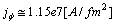 | (35) |
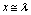 . For
. For 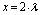 , the current density decreases at
, the current density decreases at 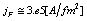 Note that velocity
Note that velocity 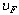 , moreover, if one considers the monopole current given by equation as
, moreover, if one considers the monopole current given by equation as 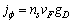 where the magnetic charge is:
where the magnetic charge is: 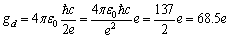 | (36) |
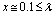 , then the current is obtained by derivation of (19.1):
, then the current is obtained by derivation of (19.1):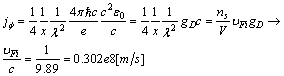 | (37) |
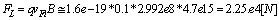 | (38) |
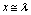 , for the upper limit:
, for the upper limit: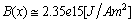 | (39) |
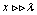 , we have
, we have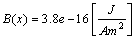 | (40) |
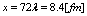 then, the force becomes
then, the force becomes 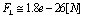 , or in terms of energy
, or in terms of energy 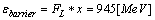 | (41) |
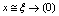 , in (17)
, in (17)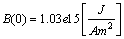 | (42) |
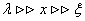 ) from (16):
) from (16):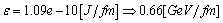 | (43) |
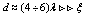 , we have
, we have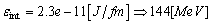 | (44) |
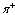 , composed of a pair of quarks
, composed of a pair of quarks 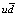 interacting at a distance
interacting at a distance 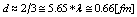 of the radius of the nucleus.Now, others important values of energy:
of the radius of the nucleus.Now, others important values of energy: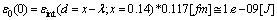 | (45) |
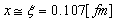 | (46) |
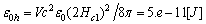 | (47) |
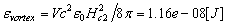 | (47.1) |
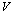 -is the volume, see fig.1a, fig.1b, accordingly, the corresponding equivalently masses are
-is the volume, see fig.1a, fig.1b, accordingly, the corresponding equivalently masses are 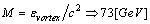 , which seems to be equal to the mass of
, which seems to be equal to the mass of 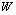 boson.The energy of the neutral boson
boson.The energy of the neutral boson 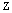 is assimilated with the vortex-vortex three pairs interaction energy[24],
is assimilated with the vortex-vortex three pairs interaction energy[24], 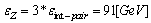 , when from (27)
, when from (27) 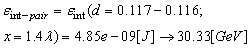 | (48) |
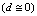 vortices lines which interacting (repel) at the center of the triangle situated at
vortices lines which interacting (repel) at the center of the triangle situated at 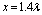 , thus, being generated a neutral current in the zone of
, thus, being generated a neutral current in the zone of 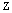 during the triangular arrangement of the lattice, see fig.1a, or fig.1b.Now, is possible that the vortices start to coalesce into a giant vortex (GV)[26], see, fig. 1b. ,Thus, from (27), results an another energy state-maximum possible (
during the triangular arrangement of the lattice, see fig.1a, or fig.1b.Now, is possible that the vortices start to coalesce into a giant vortex (GV)[26], see, fig. 1b. ,Thus, from (27), results an another energy state-maximum possible (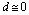 ), probable that of Higgs boson (H):
), probable that of Higgs boson (H):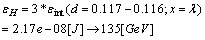 Notice that this is not in fact a particle, since contain others subparticles (
Notice that this is not in fact a particle, since contain others subparticles (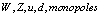 ), so during high energy protons collision (CERN) can not be obtained as itself. Here, a factor of
), so during high energy protons collision (CERN) can not be obtained as itself. Here, a factor of 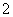 was introduced to correct on
was introduced to correct on 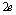 for “pairs” in the G-L model.
for “pairs” in the G-L model.3. The Photonuclear Reaction Mechanism in G-L theory
- Like in[2a], we use only the processes when a single incident photon with insufficient energy to create a normal-state belt but initiating a subsequent single-vortex crossing, which provides the rest of the energy needed to create the normal-state belt (vortex-assisted single photon count). We derive the current dependence of the rate of vortex assisted photon counts. Hence, our general picture is that the vortex crossing may trigger the
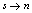 transition. A photon makes this process much more probable by creating a spot with suppressed order parameter and thus with lower energy barrier for vortex crossing. As in[2a], we derive the energy barrier for vortex crossing and crossing rate from the standard Ginzburg-Landau (GL) functional with respect to the superconducting order parameter
transition. A photon makes this process much more probable by creating a spot with suppressed order parameter and thus with lower energy barrier for vortex crossing. As in[2a], we derive the energy barrier for vortex crossing and crossing rate from the standard Ginzburg-Landau (GL) functional with respect to the superconducting order parameter 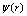 (normalized to its zero-field value in the absence of current) and the vector potential
(normalized to its zero-field value in the absence of current) and the vector potential 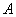 in the presence of monopoles current induced magnetic field
in the presence of monopoles current induced magnetic field 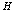 . The Gibbs energy is given by (30).Like in[2], we assume that in sufficiently narrow strips,
. The Gibbs energy is given by (30).Like in[2], we assume that in sufficiently narrow strips, 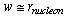 , (a) the cloud covers the entire width of strip when it reaches its maximum size, (b) the quasiparticle density in the cloud (hot belt) is close to uniform, and (c) quasiparticles suppress the superconducting order parameter inside the hot belt, but their density is not sufficient to convert the hot belt to the normal state. Thus the superconducting condensation energy density
, (a) the cloud covers the entire width of strip when it reaches its maximum size, (b) the quasiparticle density in the cloud (hot belt) is close to uniform, and (c) quasiparticles suppress the superconducting order parameter inside the hot belt, but their density is not sufficient to convert the hot belt to the normal state. Thus the superconducting condensation energy density 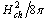 in the hot belt satisfies the inequalities
in the hot belt satisfies the inequalities 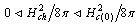 .It follows that the vortex crossing rate via hot belt (denoted by subscript
.It follows that the vortex crossing rate via hot belt (denoted by subscript 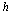 ),
), 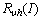 , is enhanced in comparison with that for dark counts, because the parameter
, is enhanced in comparison with that for dark counts, because the parameter 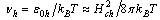 is reduced in comparison with
is reduced in comparison with 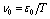 , and
, and 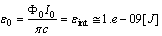 , from (45)There are three superconducting current-biased regions to be considered, which are separated by three characteristic currents
, from (45)There are three superconducting current-biased regions to be considered, which are separated by three characteristic currents 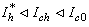 . For currents below
. For currents below 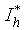 counts are absent, because vortex crossings do not result in the formation of normal-state belt. The “hot” current
counts are absent, because vortex crossings do not result in the formation of normal-state belt. The “hot” current 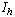 is determined through the energy balance for destroying the superconducting condensate in the hot belt similar to that for dark counts, however, with the thermodynamic field
is determined through the energy balance for destroying the superconducting condensate in the hot belt similar to that for dark counts, however, with the thermodynamic field 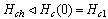 , from (24)For lower currents in the interval
, from (24)For lower currents in the interval 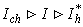 , the rate of photon counts shows a power-law current dependence,
, the rate of photon counts shows a power-law current dependence,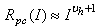 Here, we model the temperature dependent parameters
Here, we model the temperature dependent parameters 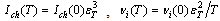 , with
, with 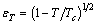 .For currents
.For currents 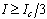 , the energy released by phase slip is sufficient to destroy superconductivity. In the region
, the energy released by phase slip is sufficient to destroy superconductivity. In the region 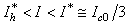 , vortex crossings via the hot belt destroy the superconducting state inside the belt during the time
, vortex crossings via the hot belt destroy the superconducting state inside the belt during the time 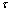 of the hot spot’s lifetime. During this time, the belt is in the normal state, which causes the “vortex-assisted” photon count.Hence, our general picture is that the vortex crossing may trigger the
of the hot spot’s lifetime. During this time, the belt is in the normal state, which causes the “vortex-assisted” photon count.Hence, our general picture is that the vortex crossing may trigger the 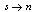 transition. A photon makes this process much more probable by creating a spot with suppressed order parameter and thus with lower energy barrier for vortex crossing. A sketch of the strip and of the belt across are shown in Fig. 2.
transition. A photon makes this process much more probable by creating a spot with suppressed order parameter and thus with lower energy barrier for vortex crossing. A sketch of the strip and of the belt across are shown in Fig. 2.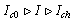 , the rate of single photon counts,
, the rate of single photon counts, 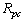 , is the same as the rate for hot spot formation
, is the same as the rate for hot spot formation 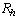 because the barrier for vortex crossing is now absent. For hot counts
because the barrier for vortex crossing is now absent. For hot counts 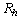 , we have
, we have 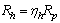 , where
, where 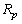 is the photon rate and
is the photon rate and 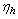 is the quantum efficiency of hot spot formation caused by a single photon.The vortex assisted photon count rate[2a] is:
is the quantum efficiency of hot spot formation caused by a single photon.The vortex assisted photon count rate[2a] is: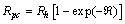 | (49) |
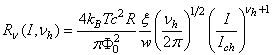 | (50) |
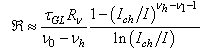 | (51) |
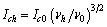 | (52) |
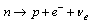 , or
, or 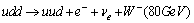 or
or 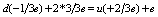 or,
or, 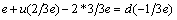 | (53) |
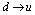 ), then this is accompanied by a release of a W boson or the crossing vortex in this model.We can suppose than along the hot belt induced by the incident photon , the charge
), then this is accompanied by a release of a W boson or the crossing vortex in this model.We can suppose than along the hot belt induced by the incident photon , the charge 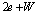 creates a bias current(
creates a bias current(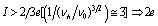 who circulates due of the potential difference between the vortex and the rest of isotope.At the first sight, the ohmic resistance of this ad-hoc electrical circuit created by the bias current is given as:
who circulates due of the potential difference between the vortex and the rest of isotope.At the first sight, the ohmic resistance of this ad-hoc electrical circuit created by the bias current is given as: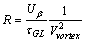 | (54) |
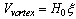 ,
, 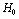 from (30.1), and the power is
from (30.1), and the power is 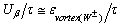 , where
, where 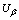 is given by (47.1) , and
is given by (47.1) , and 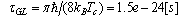 -the Ginzburg-Landau life time of
-the Ginzburg-Landau life time of 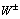 bosons.Numerically, with
bosons.Numerically, with 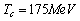 ,
, 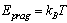 , result
, result 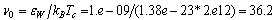 , where
, where 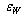 from (43);
from (43); 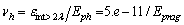 , where
, where 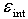 from (46).The value of
from (46).The value of 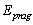 is determined by trials in order to have
is determined by trials in order to have 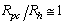 .So, based on the above models[1,2], a photonuclear reaction is viewed as an incident photon creating superconducting hot spot (hot belt) across nucleon from the composition of a unstable nuclide (radioisotope), followed by a thermally induced vortex crossing, which turns superconducting hot belt into the normal state (vacuum) resulting in a vortex assisted photon beta decay.So, with the above data related on energies of vortex and on currents from inside of the nucleon, are calculated the beta decay rates.Thus, let us discuss the
.So, based on the above models[1,2], a photonuclear reaction is viewed as an incident photon creating superconducting hot spot (hot belt) across nucleon from the composition of a unstable nuclide (radioisotope), followed by a thermally induced vortex crossing, which turns superconducting hot belt into the normal state (vacuum) resulting in a vortex assisted photon beta decay.So, with the above data related on energies of vortex and on currents from inside of the nucleon, are calculated the beta decay rates.Thus, let us discuss the 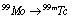 isotopes, which are widely used as SPECT isotopes[1]. The
isotopes, which are widely used as SPECT isotopes[1]. The 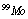 (
(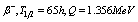 ) isotopes are produced by
) isotopes are produced by 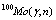 reactions and also
reactions and also 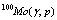 reactions followed by
reactions followed by 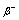 decays. CPIT with
decays. CPIT with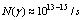 and enriched
and enriched 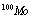 isotopes provides the RIs of
isotopes provides the RIs of 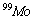 and
and 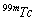 with the production rate of
with the production rate of 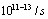 , and the RI density of
, and the RI density of 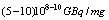 but after sufficiently long irradiation (240h).Since the product
but after sufficiently long irradiation (240h).Since the product 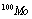 have the same decay rate as the reaction rate, we can not say if the beta decay itself is accelerated or no. In order to say that, it needs to have data on longer lived beta decay products. Thus, from our model results the same beta decay rate of
have the same decay rate as the reaction rate, we can not say if the beta decay itself is accelerated or no. In order to say that, it needs to have data on longer lived beta decay products. Thus, from our model results the same beta decay rate of 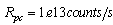 , with the incident photon rate of
, with the incident photon rate of 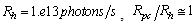 , or the same happens, i.e. much faster ( instantly), if the photons energy will be at threshold value
, or the same happens, i.e. much faster ( instantly), if the photons energy will be at threshold value 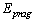 , see fig.3.The same type of instant rates it happens for all beta-decay isotopes, like:
, see fig.3.The same type of instant rates it happens for all beta-decay isotopes, like: 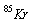 ,
, 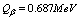 and
and 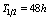 ,
, 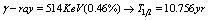 ;
;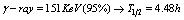
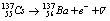 ,
,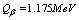 ,
, 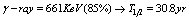 etc., i.e. these rates are not dependent of the nuclide type, are dependent only on
etc., i.e. these rates are not dependent of the nuclide type, are dependent only on 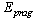 .
.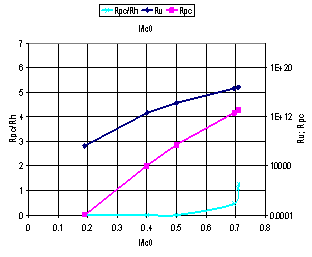 | Figure 3. The vortex-assisted photon count rate 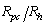 vs. bias current given in Eqs. vs. bias current given in Eqs. 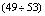 |
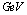 electrons stored in a storage ring lose little their energy via interactions with laser photons, they remain in the ring. The laser electron photons are efficiently used for production of desired
electrons stored in a storage ring lose little their energy via interactions with laser photons, they remain in the ring. The laser electron photons are efficiently used for production of desired 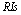 . Then the overall efficiency of the
. Then the overall efficiency of the 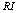 production is many orders of magnitude larger than that of the charged particle accelerators and nuclear reactors. Fast neutrons are used for nuclear transmutation but only a small fraction of the charged particles are used to produce the fast neutrons. Intense electron accelerators provide bremestrahlung photons for photonuclear isotope transmutation but most of photons are below the threshold energy of the photonuclear reaction. There are several programs of intense photon sources under progress MAGa-ray is the project at LLNL for high intensity photons with
production is many orders of magnitude larger than that of the charged particle accelerators and nuclear reactors. Fast neutrons are used for nuclear transmutation but only a small fraction of the charged particles are used to produce the fast neutrons. Intense electron accelerators provide bremestrahlung photons for photonuclear isotope transmutation but most of photons are below the threshold energy of the photonuclear reaction. There are several programs of intense photon sources under progress MAGa-ray is the project at LLNL for high intensity photons with 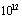 photons/sec in the MeV region and ELI-NP is the one at Romania[35] for higher energy photons with
photons/sec in the MeV region and ELI-NP is the one at Romania[35] for higher energy photons with 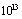 photons/sec in the GR energy region of
photons/sec in the GR energy region of 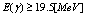 . They plan to achieve the intensity of around
. They plan to achieve the intensity of around 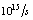 . In Tokai Japan, the ERL(Energy Recovery Liniac) project is under progress to provide intense photons for resonance fluorescence
. In Tokai Japan, the ERL(Energy Recovery Liniac) project is under progress to provide intense photons for resonance fluorescence4. Beta Decay Halftime Calculation by G-L Theory
- Below we will demonstrate that the mechanism for beta decay of radioisotopes is the same as the dark counts in the case of superconductors[2b].In[2], are discussed three types of possible fluctuations in superconducting strip (assimilated in our case with the nucleon) which result in dissipation. (a) Spontaneous nucleation of a normal-state belt across the strip with
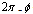 phase slip as in thin wires (a every phase slip meaning
phase slip as in thin wires (a every phase slip meaning 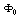 energy released). (b) Spontaneous nucleation of a single vortex near the edge of the strip and its motion across to the opposite edge accompanied by a voltage pulse. (c) Spontaneous nucleation of vortex-antivortex pairs and their unbinding as they move across the strip to opposite edges due to the Lorentz force, as well as the opposite process of nucleation of vortices and antivortices at the opposite edges and their annihilation in the strip middle. In[2b] are derived the energy barriers for three dissipative processes mentioned within the
energy released). (b) Spontaneous nucleation of a single vortex near the edge of the strip and its motion across to the opposite edge accompanied by a voltage pulse. (c) Spontaneous nucleation of vortex-antivortex pairs and their unbinding as they move across the strip to opposite edges due to the Lorentz force, as well as the opposite process of nucleation of vortices and antivortices at the opposite edges and their annihilation in the strip middle. In[2b] are derived the energy barriers for three dissipative processes mentioned within the 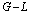 theory. Consider a thin-film strip (one of three vortexes of the nucleus) of width
theory. Consider a thin-film strip (one of three vortexes of the nucleus) of width 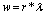 , see fig 1a, fig.1b. We choose the coordinates so that
, see fig 1a, fig.1b. We choose the coordinates so that 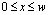 . Since we are interested in bias currents which may approach depairing values, the suppression of the superconducting order parameter
. Since we are interested in bias currents which may approach depairing values, the suppression of the superconducting order parameter 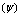 must be taken into account. Also in[2b], is used the standard GL functional , given above in (1). We will use the case (a), a vortex crossing from one strip edge to the opposite one induces a phase slip without creating a normal region across the strip (one of three vortexes of nucleus) width. When, is treating the vortex as a particle moving in the energy potential formed by the superconducting currents around vortex center inside the strip and by the Lorentz force induced by the bias current. In[2b], it was derived the energy potential and is found the vortex crossings rate (phase slips and corresponding voltage pulses) in the framework of Langevin equation for viscous vortex motion by invoking the known solution of the corresponding Fokker-Planck equation.Finally, from[2] the asymptotic estimate for the dark counts rate, results as:
must be taken into account. Also in[2b], is used the standard GL functional , given above in (1). We will use the case (a), a vortex crossing from one strip edge to the opposite one induces a phase slip without creating a normal region across the strip (one of three vortexes of nucleus) width. When, is treating the vortex as a particle moving in the energy potential formed by the superconducting currents around vortex center inside the strip and by the Lorentz force induced by the bias current. In[2b], it was derived the energy potential and is found the vortex crossings rate (phase slips and corresponding voltage pulses) in the framework of Langevin equation for viscous vortex motion by invoking the known solution of the corresponding Fokker-Planck equation.Finally, from[2] the asymptotic estimate for the dark counts rate, results as: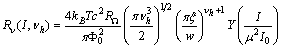 | (55) |
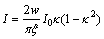 | (56) |
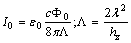 | (57) |
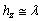 -the axial (z) height of the monopole condensate.Here, the critical current at which the energy barrier vanishes for a single vortex crossing:
-the axial (z) height of the monopole condensate.Here, the critical current at which the energy barrier vanishes for a single vortex crossing: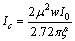 | (58) |
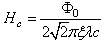 | (59) |
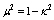 , and
, and 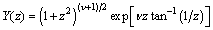 | (60) |
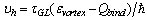 -is the energy of the vortex during crossing the barrier of height
-is the energy of the vortex during crossing the barrier of height 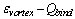 by quantum tunneling in place of the thermal activation used in[2b], and overpassing an ohmic resistance along a transverse path way of the nuclide:
by quantum tunneling in place of the thermal activation used in[2b], and overpassing an ohmic resistance along a transverse path way of the nuclide: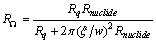 | (61) |
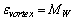 from (47.1), and
from (47.1), and 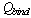 is the beta decay energy as obtained from the data of each radionuclide of beta decay type (Nuclides chart 2010).In the case of beta disintegration
is the beta decay energy as obtained from the data of each radionuclide of beta decay type (Nuclides chart 2010).In the case of beta disintegration 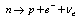 , or
, or 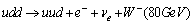 , or and the bias current is:
, or and the bias current is: 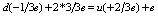 In
In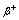 decay, energy is used to convert a proton into a neutron, while emitting a positron (
decay, energy is used to convert a proton into a neutron, while emitting a positron (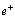 ) and an electron neutrino (
) and an electron neutrino (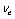 ):
):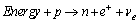 In all the cases where
In all the cases where 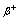 decay is allowed energetically (and the proton is a part of a nucleus with electron shells) it is accompanied by the electron capture (EC) process, when an atomic electron is captured by a nucleus with the emission of a neutrino:
decay is allowed energetically (and the proton is a part of a nucleus with electron shells) it is accompanied by the electron capture (EC) process, when an atomic electron is captured by a nucleus with the emission of a neutrino: 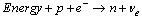 Therefore, the ad-hoc bias current created during vortex crossing through the energy barrier is:
Therefore, the ad-hoc bias current created during vortex crossing through the energy barrier is: 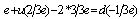 At the first sight, the ohmic resistance of this ad-hoc electrical circuit created by the bias current
At the first sight, the ohmic resistance of this ad-hoc electrical circuit created by the bias current 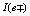 due of quarks transformation
due of quarks transformation 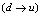 , or
, or 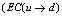 , is given as:
, is given as: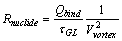 | (62) |
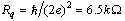 , where the vortex potential is
, where the vortex potential is 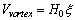 ,
, 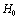 from (9)Giordano[21] has suggested that phase slips due to macroscopic quantum tunneling may be the cause of the low temperature resistance tail in the 1D wires he studied in zero field. One possible mechanism for our low temperature resistivity tail could be quantum tunneling of vortices through the energy barrier[22]. One expects a crossover from thermal activation to quantum tunneling to occur when[23], in (55) in place of thermal activation we use the quantum tunneling:
from (9)Giordano[21] has suggested that phase slips due to macroscopic quantum tunneling may be the cause of the low temperature resistance tail in the 1D wires he studied in zero field. One possible mechanism for our low temperature resistivity tail could be quantum tunneling of vortices through the energy barrier[22]. One expects a crossover from thermal activation to quantum tunneling to occur when[23], in (55) in place of thermal activation we use the quantum tunneling: 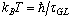 A vortex moving from
A vortex moving from 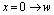 , during the time
, during the time 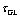 .We estimate the total interaction energy interaction with the neighborhood vortexes or with the one giant-vortexes, fig.1b, of others nucleons from the nuclide nucleus, during the time
.We estimate the total interaction energy interaction with the neighborhood vortexes or with the one giant-vortexes, fig.1b, of others nucleons from the nuclide nucleus, during the time 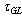 along the vortex path by matching (56), (57) and (59) as:
along the vortex path by matching (56), (57) and (59) as: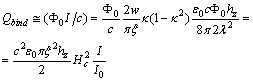 | (63) |
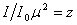 was chosen as a variable in (55), through (60); This is, in fact, the work done by the Lorentz force on the vortex path of the length
was chosen as a variable in (55), through (60); This is, in fact, the work done by the Lorentz force on the vortex path of the length  .Now, we proceed to application to some radionuclides which decay beta, and beginning with the neutron. Thus, the lifetime of the free neutron is a basic physical quantity, which is relevant in a variety of different fields of particle and astrophysics. Being directly related to the weak interaction characteristics it plays a vital role in the determination of the basic parameters like coupling constants or quark mixing angles as well as for all cross sections related to weak
.Now, we proceed to application to some radionuclides which decay beta, and beginning with the neutron. Thus, the lifetime of the free neutron is a basic physical quantity, which is relevant in a variety of different fields of particle and astrophysics. Being directly related to the weak interaction characteristics it plays a vital role in the determination of the basic parameters like coupling constants or quark mixing angles as well as for all cross sections related to weak  interaction. From the most precise measurement within this class of experiments, results
interaction. From the most precise measurement within this class of experiments, results 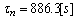 .From Nuclide chart-2010, result:
.From Nuclide chart-2010, result: 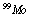 (
(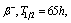
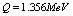 );
); 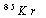 ,
, 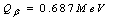 and
and 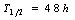 ,
, 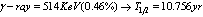 ;
;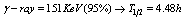 ;
; 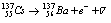 ,
,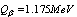 ,
, 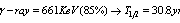 etcNumerically, with these data result:
etcNumerically, with these data result: 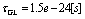 ,
, 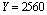 ,
, 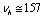 , and with
, and with 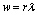 as variable, the evolution of dark count rate
as variable, the evolution of dark count rate 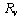 , and of
, and of 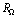 , for different isotopes are given in fig. 3.Here, the fraction of the bias current to critical current
, for different isotopes are given in fig. 3.Here, the fraction of the bias current to critical current 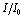 as used in
as used in 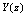 from (60): was deduced separately for
from (60): was deduced separately for 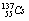 as that of the plateau zone in fig.4 , respectively of
as that of the plateau zone in fig.4 , respectively of 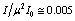 , by using the condition
, by using the condition 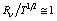 . We can observe that this value corresponds with the expected value from quarks transformation of
. We can observe that this value corresponds with the expected value from quarks transformation of 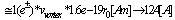 , where the vortex crossing velocity is
, where the vortex crossing velocity is 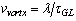 , and
, and 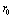 -K shell radius. Therefore, the bias current, which is perpendicularly on the monopoles current, is
-K shell radius. Therefore, the bias current, which is perpendicularly on the monopoles current, is 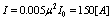 ; where,
; where, 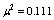 , and the monopoles current is:
, and the monopoles current is: 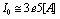 as given by (57), and
as given by (57), and 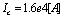 from (58). From (62), results
from (58). From (62), results 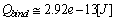 or near equally with
or near equally with 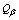 of the almost of nuclides, for example, for
of the almost of nuclides, for example, for 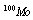 ,
, 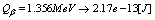 . Now, in case of quantum tunneling the transmission coefficient[20] is
. Now, in case of quantum tunneling the transmission coefficient[20] is 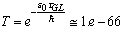 , which is too small, so, a vortex crossing from one strip edge to the opposite one induces a phase slip, case a), is the only viabile mechanism for dark counts (beta decay).Thus, it was established a logarithmic equation of the
, which is too small, so, a vortex crossing from one strip edge to the opposite one induces a phase slip, case a), is the only viabile mechanism for dark counts (beta decay).Thus, it was established a logarithmic equation of the 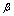 decay rate which resulting a straight line as a function of the barrier width
decay rate which resulting a straight line as a function of the barrier width 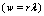 for every nuclide, fig.4, it decreasing in case of long lived nuclides, like
for every nuclide, fig.4, it decreasing in case of long lived nuclides, like 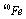 . Therefore, this evolution is a decisive validation test of entirely model. The factor
. Therefore, this evolution is a decisive validation test of entirely model. The factor 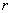 describe the interactions of the nucleons inside of the nucleus, being a complex function of
describe the interactions of the nucleons inside of the nucleus, being a complex function of 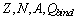 .
. 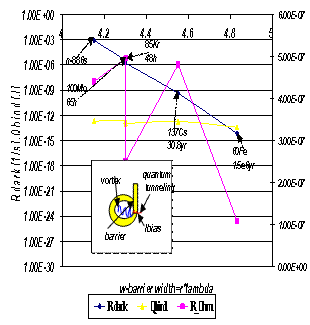 | Figure 4. The evolution of dark count (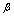 decay) rate as function of barrier width decay) rate as function of barrier width |
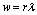 ?In order to answer to this question, in the following we will look to the vortexes interactions[24] vis-à-vis of the nucleus substructure models
?In order to answer to this question, in the following we will look to the vortexes interactions[24] vis-à-vis of the nucleus substructure models 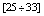 .Thus, firstly, from[24], for vortex-vortex interaction (V-V) at large separation, using the asymptotic form of the modified Bessel functions, is:
.Thus, firstly, from[24], for vortex-vortex interaction (V-V) at large separation, using the asymptotic form of the modified Bessel functions, is: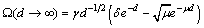 | (64) |
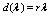 -the separation distance;
-the separation distance; 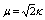 , and
, and 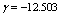 ;
; 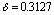 are fitting parameters of the analytical fitting function for the numerically obtained curves by using the finite difference technique and a relaxation method for the Euler-Lagrange equations for the present problem setting.Furthermore, in[24], is show that the interaction between an antivortex and a giant vortex is always attractive as well. In the absence of lateral confinement, a giant vortex is a stable (unstable) state in type-I (type-II) systems and can interact as such with other vortices, and this motivated us to investigate the interaction force between a vortex and a giant vortex.
are fitting parameters of the analytical fitting function for the numerically obtained curves by using the finite difference technique and a relaxation method for the Euler-Lagrange equations for the present problem setting.Furthermore, in[24], is show that the interaction between an antivortex and a giant vortex is always attractive as well. In the absence of lateral confinement, a giant vortex is a stable (unstable) state in type-I (type-II) systems and can interact as such with other vortices, and this motivated us to investigate the interaction force between a vortex and a giant vortex.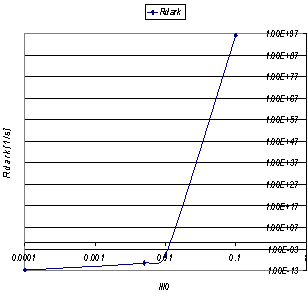 | Figure 5. The evolution of the dark count rate (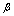 ) decay as a function of the bias current ) decay as a function of the bias current |
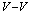 , but also for the
, but also for the 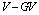 interaction force.
interaction force.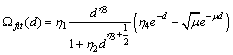 | (65) |
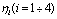 are four fitting parameters.The values of the four fitting parameters are given in Table
are four fitting parameters.The values of the four fitting parameters are given in Table 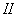 of[ 24 ], for
of[ 24 ], for  from
from 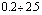 In our case
In our case 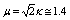 ; result:
; result: 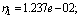
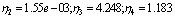 In the previous subsections, we showed that when two vortices or a vortex and a giant vortex are brought close to each other, they merge forming a single giant vortex state with vorticity
In the previous subsections, we showed that when two vortices or a vortex and a giant vortex are brought close to each other, they merge forming a single giant vortex state with vorticity 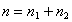 , and in the limit of small separation the
, and in the limit of small separation the 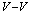 or
or 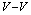 forces are very weak. Conversely, a vortex and an antivortex attract and annihilate, both in type-I and type-II superconductors. In what follows, the behavior of the force for the vortex-antivortex
forces are very weak. Conversely, a vortex and an antivortex attract and annihilate, both in type-I and type-II superconductors. In what follows, the behavior of the force for the vortex-antivortex 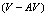 interaction as a function of the
interaction as a function of the 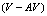 separation is also studied. As follows from theory[24], the V-AV interaction is always attractive.However, at some critical
separation is also studied. As follows from theory[24], the V-AV interaction is always attractive.However, at some critical 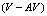 separation
separation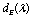 , the solution with well defined supercurrents around each vortex and antivortex ceases to be the lowest energy state of the system. A solution with lower energy exhibits a strong suppression of the amplitude of the order parameter and super-current in the region between the vortex and the antivortex, and represents the ground state for small
, the solution with well defined supercurrents around each vortex and antivortex ceases to be the lowest energy state of the system. A solution with lower energy exhibits a strong suppression of the amplitude of the order parameter and super-current in the region between the vortex and the antivortex, and represents the ground state for small 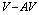 distances. A hysteresis is observed in the vicinity of the critical separation
distances. A hysteresis is observed in the vicinity of the critical separation 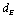 . The dependence of the numerically obtained critical separation
. The dependence of the numerically obtained critical separation 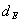 for the
for the 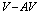 interaction on the GL parameter
interaction on the GL parameter 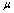 is illustrated as the squares in Fig. 11(c) from Ref.[ ], and can be fitted to a function similar to the one used for the critical separations in the
is illustrated as the squares in Fig. 11(c) from Ref.[ ], and can be fitted to a function similar to the one used for the critical separations in the 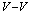 and
and 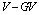 , given by and becomes unstable as the
, given by and becomes unstable as the 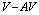 separation is reduced at
separation is reduced at 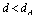 , while the solution with suppressed current and order parameter between the vortex and antivortex, shown by the gray curves, becomes the lowest energy state for
, while the solution with suppressed current and order parameter between the vortex and antivortex, shown by the gray curves, becomes the lowest energy state for 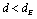 and the only stable solution for
and the only stable solution for 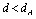 .The suppressed order parameter in the region between vortices observed in the only stable solution for
.The suppressed order parameter in the region between vortices observed in the only stable solution for 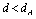 suggests that a vortex and an antivortex cannot coexist at these distances, unless somehow pinned, in which case this string solution is formed. This is reasonable, since at
suggests that a vortex and an antivortex cannot coexist at these distances, unless somehow pinned, in which case this string solution is formed. This is reasonable, since at 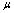 and can be fitted by :
and can be fitted by :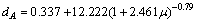 ; or
; or 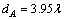 When the
When the 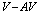 separation is large, the currents around the vortex and short distances the fields of the vortex and the antivortex compensate each other, and the flux quantization as an essential property of a(n) (anti)vortex is lost. Notice that this is different from the case of two merging vortices, which can coexist at short distances, deform and interact as described in previous sections, since the flux quantization of the
separation is large, the currents around the vortex and short distances the fields of the vortex and the antivortex compensate each other, and the flux quantization as an essential property of a(n) (anti)vortex is lost. Notice that this is different from the case of two merging vortices, which can coexist at short distances, deform and interact as described in previous sections, since the flux quantization of the 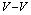 pair is preserved even at small
pair is preserved even at small 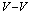 separations. For molecular dynamics studies of the
separations. For molecular dynamics studies of the 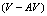 motion, one should consider the critical separation
motion, one should consider the critical separation 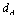 as the separation where the
as the separation where the 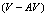 pair annihilates.The fit of the numerically obtained
pair annihilates.The fit of the numerically obtained 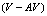 interaction force for
interaction force for 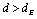 , yields a single expression:
, yields a single expression: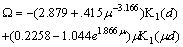 | (66) |
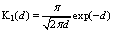 which is expected to provide an accurate description of the V-AV interaction force, at separations
which is expected to provide an accurate description of the V-AV interaction force, at separations 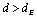 , for any value of
, for any value of 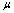 .Thus, in[25] is mentioned that the results obtained the study of “Effect of a fermion on quantum phase transitions in bosonic systems” are of interest not only for applications to nuclei, but also for applications to other systems in which a fermion is immersed in a bath of bosons, for example, the simple case of a spin
.Thus, in[25] is mentioned that the results obtained the study of “Effect of a fermion on quantum phase transitions in bosonic systems” are of interest not only for applications to nuclei, but also for applications to other systems in which a fermion is immersed in a bath of bosons, for example, the simple case of a spin 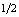 particle in a bath of harmonic oscillator bosons[34] page 217. In the literature[25] of the Interacting Boson Fermion Model (IBM ) the bosonic part has a cubic term leading to the possibility of a first order transition. The analogy with bosonic systems in an external field also suggests that these results apply to the study of phase transition in superconductors in the presence of magnetic fields(which is our case of phase slip, as discussed above). Atomic nuclei are known to exhibit changes of their energy levels and electromagnetic transition rates among them when the number of protons and/or neutrons is modified, resulting in shape phase transitions from one kind of collective behaviour to another. These transitions are not phase transitions of the usual thermodynamic type. They are quantum phase transitions
particle in a bath of harmonic oscillator bosons[34] page 217. In the literature[25] of the Interacting Boson Fermion Model (IBM ) the bosonic part has a cubic term leading to the possibility of a first order transition. The analogy with bosonic systems in an external field also suggests that these results apply to the study of phase transition in superconductors in the presence of magnetic fields(which is our case of phase slip, as discussed above). Atomic nuclei are known to exhibit changes of their energy levels and electromagnetic transition rates among them when the number of protons and/or neutrons is modified, resulting in shape phase transitions from one kind of collective behaviour to another. These transitions are not phase transitions of the usual thermodynamic type. They are quantum phase transitions 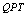 [25] (initially called ground state phase transitions ). However, since the proton-neutron quadrupole interaction dominates over the proton-proton and neutron-neutron ones for medium-heavy and heavy deformed nuclei, the axial deformation parameters
[25] (initially called ground state phase transitions ). However, since the proton-neutron quadrupole interaction dominates over the proton-proton and neutron-neutron ones for medium-heavy and heavy deformed nuclei, the axial deformation parameters 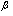 are related by a constant of proportionality determined by equating the corresponding intrinsic quadrupole moments. The geometrical variable
are related by a constant of proportionality determined by equating the corresponding intrinsic quadrupole moments. The geometrical variable 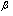 is obtained by multiplying the boson. The nuclear
is obtained by multiplying the boson. The nuclear 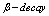 provides a severe test of the nuclear model because the decay rates are very sensitive to the wave functions of both the initial and the final nuclei.The description of β decay of odd-mass nuclei in the interacting boson-fermion model (IBFM) was formulated by[25].Thus, in[25], are presented the results of an investigation of the effect of a fermion ( in our case the electron
provides a severe test of the nuclear model because the decay rates are very sensitive to the wave functions of both the initial and the final nuclei.The description of β decay of odd-mass nuclei in the interacting boson-fermion model (IBFM) was formulated by[25].Thus, in[25], are presented the results of an investigation of the effect of a fermion ( in our case the electron 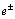 ) on QPTs in bosonic systems. That is done in atomic nuclei by making use of the Interacting Boson Fermion Model (
) on QPTs in bosonic systems. That is done in atomic nuclei by making use of the Interacting Boson Fermion Model (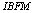 ), a model of odd-even nuclei in terms of correlated pairs with angular momentum
), a model of odd-even nuclei in terms of correlated pairs with angular momentum 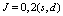 and unpaired particles with angular momentum
and unpaired particles with angular momentum 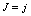 (
(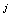 fermions). To note, however, that the method of analysis from[25] can also be used for systems with other values of the fermion,
fermions). To note, however, that the method of analysis from[25] can also be used for systems with other values of the fermion, 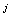 , and boson,
, and boson, 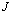 , angular momenta, for example the spin-boson systems, the simplest case of which is a fermion with
, angular momenta, for example the spin-boson systems, the simplest case of which is a fermion with 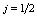 (
(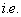 , a single spin) in a bath of harmonic oscillator one-dimensional bosons of interest in dissipation and light phenomena. Here the focus is on the effect of a fermionic impurity on
, a single spin) in a bath of harmonic oscillator one-dimensional bosons of interest in dissipation and light phenomena. Here the focus is on the effect of a fermionic impurity on 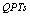 in bosonic systems. The main results are that,
in bosonic systems. The main results are that, 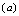 the presence of a single fermion greatly influences the location and nature of the phase transition, the fermion acting either as a catalyst or a retarder of the
the presence of a single fermion greatly influences the location and nature of the phase transition, the fermion acting either as a catalyst or a retarder of the 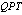 , and
, and 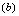 there is experimental evidence for quantum phase transitions in odd-even nuclei (bosonic systems plus a single fermion).A main conclusion from[25] is that the effect of the fermionic impurity is to wash out the phase transition for states with quantum numbers:
there is experimental evidence for quantum phase transitions in odd-even nuclei (bosonic systems plus a single fermion).A main conclusion from[25] is that the effect of the fermionic impurity is to wash out the phase transition for states with quantum numbers: 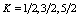 and to enhance it for states with
and to enhance it for states with 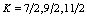 . In other words, the fermion acts as a catalyst for some states and as a retarder for others. Also, when the coupling strength becomes very large, the minima for some large
. In other words, the fermion acts as a catalyst for some states and as a retarder for others. Also, when the coupling strength becomes very large, the minima for some large 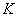 like
like 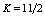 , shift to negative values (oblate deformation). An important property of atomic nuclei is that they provide experimental evidence for shape
, shift to negative values (oblate deformation). An important property of atomic nuclei is that they provide experimental evidence for shape 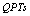 , in particular, of the spherical to axially-deformed transition
, in particular, of the spherical to axially-deformed transition 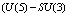 . One of three signatures have been used to experimentally verify the occurrence of shape phase transitions in nuclei, namely: the behavior of the gap between the ground state and the first excited
. One of three signatures have been used to experimentally verify the occurrence of shape phase transitions in nuclei, namely: the behavior of the gap between the ground state and the first excited 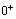 state. The nucleus
state. The nucleus 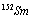 , with
, with 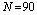 and
and 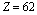 , lies intermediate between nuclei of known spherical shape and well-deformed axially-symmetric rotor structure. A sudden change in deformation occurs at
, lies intermediate between nuclei of known spherical shape and well-deformed axially-symmetric rotor structure. A sudden change in deformation occurs at 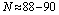 for the
for the 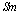 and neighboring isotopic chains , see Figure 6. New data obtained[31] constrain the description of this nucleus within the
and neighboring isotopic chains , see Figure 6. New data obtained[31] constrain the description of this nucleus within the  to parameter values near the critical point of the transition from oscillator to rotor structure. The performed IBA calculations in[31] for the entire region
to parameter values near the critical point of the transition from oscillator to rotor structure. The performed IBA calculations in[31] for the entire region  with the simple IBA Hamiltonian which involves only one parameter,
with the simple IBA Hamiltonian which involves only one parameter, 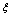 , which depends only on the neutron number
, which depends only on the neutron number 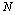 , for all the isotopic chains.Figure 6 shows that the evolution of some basic observables in
, for all the isotopic chains.Figure 6 shows that the evolution of some basic observables in 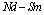 is very well reproduced by these calculations. The energy of the intrinsic excitation
is very well reproduced by these calculations. The energy of the intrinsic excitation  has a minimum at the phase transition point. The phase/shape transition is mirrored in the calculations and, as noted, the IBA parameter
has a minimum at the phase transition point. The phase/shape transition is mirrored in the calculations and, as noted, the IBA parameter 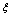 plays the role of a control parameter.The total energy surface[31] corresponding to the
plays the role of a control parameter.The total energy surface[31] corresponding to the 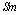 isotopes obtained from the IBA with increasing neutron number changes the location of the deformation minimum, from
isotopes obtained from the IBA with increasing neutron number changes the location of the deformation minimum, from 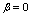 to finite
to finite 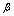 when the neutron number increases from
when the neutron number increases from  to
to  . Notice that the bosons (
. Notice that the bosons (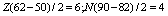 ) pairing appears for
) pairing appears for 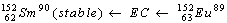 , and
, and 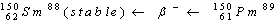 , until a free proton appears for
, until a free proton appears for 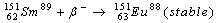 , and
, and 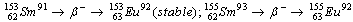 , the same situation for
, the same situation for 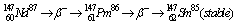 , etc.
, etc.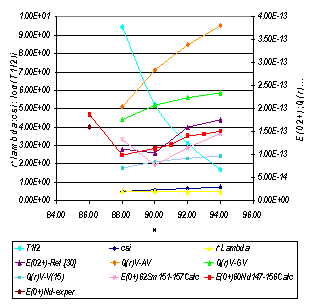 | Figure 6. The evolution of empirical values of  in the in the  isotopic chains with isotopic chains with 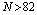 compared with the IBA results as extracted from[31], and of compared with the IBA results as extracted from[31], and of  as calculated by the present model as calculated by the present model |
 and
and  antivortex
antivortex 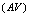 of different spin, a neutron is a Giant-vortex
of different spin, a neutron is a Giant-vortex 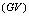 . Therefore, for
. Therefore, for 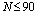 , we have an interaction
, we have an interaction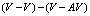 , and above of
, and above of 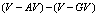 type, respectively. Based on these rationales we have obtained the values of
type, respectively. Based on these rationales we have obtained the values of 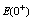 , as shown in figure
, as shown in figure  , where, we show, also, the values of interactions
, where, we show, also, the values of interactions 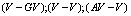 calculated with equations
calculated with equations 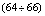 . In this model, the phase/shape changes are functions of a control parameter
. In this model, the phase/shape changes are functions of a control parameter 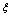 and a quadrupole deformation
and a quadrupole deformation 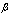 as an order parameter, and in our case the equivalently phase slip which conducts to a dark count accompanied by a
as an order parameter, and in our case the equivalently phase slip which conducts to a dark count accompanied by a 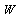 boson energy, in place of
boson energy, in place of 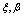 parameter appears to be necessarily only one:
parameter appears to be necessarily only one: 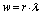 , see fig. 6. Our model have the advantage to explain the cause of phase change and its probability associated, as expressed by the inherently dark counts rate or the decay half-time
, see fig. 6. Our model have the advantage to explain the cause of phase change and its probability associated, as expressed by the inherently dark counts rate or the decay half-time  .
.5. Conclusions
- A model was developed in which a photonuclear reaction is viewed as an incident photon creating superconducting hot spot (hot belt) across nucleon from the composition of a unstable nuclide (radioisotope), followed by a thermally induced vortex crossing, which turns superconducting hot belt into the normal state (vacuum) resulting in a vortex assisted photon beta decay. Because this model, firstly developed for superconducting nanowire single-photon detector (SNSPD), requires data on energies of vortex and on currents from inside of the nucleon, an analog of a superconductor model was developed for the nucleon.Thus, it was re-visited a model G-L, in order to calculate the Lorenz force, the current, and the energies of the Abrikosov vortex lines inside of the nucleon. Thus, it was found that these energies correspond of subatomic particles,
 ,
, 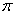 , Higgs bosons, and of meson
, Higgs bosons, and of meson 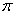 . So, the nucleon can be seen as a triangular lattice with three pairs of quarks-antiquarks in the tips of the triangle. These axial vortexes (filaments) interacting in the lateral plane. All of the keys of this model, as being analogous to a superconductor clinging very well, starting with the use of Maxwell's equation with monopoles, further mass, charge, and the number of monopoles (density), which define the penetration depth and the coherence length which could be considered as new fundamentals constants for nucleons. Also, we can say that, because no free quarks were detected, the same is true for monopoles, both of which are confined together and in full in nucleons, when the temperature of the universe has reached
. So, the nucleon can be seen as a triangular lattice with three pairs of quarks-antiquarks in the tips of the triangle. These axial vortexes (filaments) interacting in the lateral plane. All of the keys of this model, as being analogous to a superconductor clinging very well, starting with the use of Maxwell's equation with monopoles, further mass, charge, and the number of monopoles (density), which define the penetration depth and the coherence length which could be considered as new fundamentals constants for nucleons. Also, we can say that, because no free quarks were detected, the same is true for monopoles, both of which are confined together and in full in nucleons, when the temperature of the universe has reached 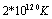 .Finally the model provides counts (decay) rates (
.Finally the model provides counts (decay) rates ( ) comparable with the experiments, and allows the estimation of intensity
) comparable with the experiments, and allows the estimation of intensity 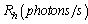 , and of threshold value of photons energy (
, and of threshold value of photons energy (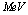 ) , in order to achieve
) , in order to achieve 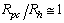 , or (
, or ( ) efficiency of beta decay type radionuclides in the frame of the nuclear transmutation in the reducing of radioactive waste, together with
) efficiency of beta decay type radionuclides in the frame of the nuclear transmutation in the reducing of radioactive waste, together with 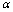 decay enhancement method[20]. As a validation test is the application of this model to the mechanism of natural beta decay viewed as dark count rate, which it was discussed in comparison with the results of one recently model on the effect of a fermion on quantum phase transitions in bosonic systems.
decay enhancement method[20]. As a validation test is the application of this model to the mechanism of natural beta decay viewed as dark count rate, which it was discussed in comparison with the results of one recently model on the effect of a fermion on quantum phase transitions in bosonic systems. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML