D. B. Fairlie1, A. N. Leznov2, R. Torres-Cordoba2, 3
1University Durham, England
2Universidad Autonoma del Estado de Morelos, CIICAp, Cuernavaca, Mexico
3Universidad Autonoma de Cd. Juarez, Chihuahua Mexico
Correspondence to: R. Torres-Cordoba, Universidad Autonoma del Estado de Morelos, CIICAp, Cuernavaca, Mexico.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The 1+2 dimensional continuous Toda chain presents a formidable challenge to the construction of solutions. Two variable reductions of the equation are known, but up till now nothing more is known. In this paper a way to solve the equation is presented, and some solutions are explicitly constructed. The method depends upon connecting series solutions of the symmetry equation of the Toda chain with the Toda solutions, as is guaranteed by general theory. Such solutions of the symmetry equation are obtainable a series method. An explicit solution is constructed by this method, and a general procedure is given to realize further solutions, which, however are given only in implicit form.
Keywords:
Toda chain, Integrable systems and Non-Linear Differential Equations
1. Introduction
The usual form of the equation under consideration is the following one;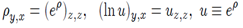 | (1) |
Here ρ(x, y, z) is an unknown function of three independent variables. This equation arises as a reduction of the Plebansky equation[1] describing self-dual four dimensional (0 + 4); (2 + 2) gravity. In this connection it was considered in[2] and in literature is known as the Boyer-Finley equation.Equation (1) can also be obtained as a limit of the discrete Toda chain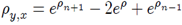 under appropriate rescaling (n→z). The series solutions of the symmetry equation for the Toda chain was found in[3].Also, a solution of the two dimensional reduction of (1) (ρ = (z, y + x) was found in implicit form in[4]. Infinite series solutions of the symmetry equation corresponding to (1) were found in[5]. But the connection between series solutions of the symmetry equation with the solution of the initial system (1) has not been discovered. However general theory gives a guarantee that each solution of symmetry equation is connected with an analytical solution of the initial system in explicit or implicit form. The goal of the present paper is to fill this gap and demonstrate a way how an analytical solution of (1) is connected with the solution constructed in[3] of the symmetry equation. In[5], thePlebansky equation was represented in the form of two equations of the first order for two unknown functions, one of which satisfies the Plebansky equation by itself, the second one satisfies the corresponding symmetry equation. It is possible to find in an independent way the solution of symmetry equation in recurrence form. As was remarked the above equation under consideration in the present paper is a reduction of the Plebansky equation and so it is possible to try to solve it by the same methods[6].
under appropriate rescaling (n→z). The series solutions of the symmetry equation for the Toda chain was found in[3].Also, a solution of the two dimensional reduction of (1) (ρ = (z, y + x) was found in implicit form in[4]. Infinite series solutions of the symmetry equation corresponding to (1) were found in[5]. But the connection between series solutions of the symmetry equation with the solution of the initial system (1) has not been discovered. However general theory gives a guarantee that each solution of symmetry equation is connected with an analytical solution of the initial system in explicit or implicit form. The goal of the present paper is to fill this gap and demonstrate a way how an analytical solution of (1) is connected with the solution constructed in[3] of the symmetry equation. In[5], thePlebansky equation was represented in the form of two equations of the first order for two unknown functions, one of which satisfies the Plebansky equation by itself, the second one satisfies the corresponding symmetry equation. It is possible to find in an independent way the solution of symmetry equation in recurrence form. As was remarked the above equation under consideration in the present paper is a reduction of the Plebansky equation and so it is possible to try to solve it by the same methods[6].
2. Preliminary Manipulations. Short Excursion into[3]
Let us rewrite (1) in the form of a system of two equations of the first degree.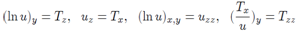 | (2) |
or as the initial equation is symmetrical with respect to exchange of the variables x, y, the following is also a possible form;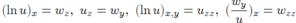 | (3) |
The symmetry equation arises from the initial one after differentiation by an arbitrary parameter and considering this derivative as a new unknown function. In the case under consideration this equation is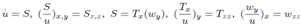 It is necessary to understand the last manipulation in such way, that if we represent the solution of the symmetry equation in the form S = Tx or S = wy then the last equations in (2), (3) are exactly the symmetry equation by itself. Finally a linear system of equations of first order for the function u function is
It is necessary to understand the last manipulation in such way, that if we represent the solution of the symmetry equation in the form S = Tx or S = wy then the last equations in (2), (3) are exactly the symmetry equation by itself. Finally a linear system of equations of first order for the function u function is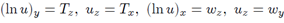 | (4) |
In[3] we have obtained series solutions of the symmetry equation in integro-differential terms of the function u. Thus it is possible use these expressions in the system T, u and obtain two self consistent equation in-stead of only one equation for the function u. It is obvious that in this way we will not be able to obtain a general solution for the equation for u but only its partial soliton like series solutions. Solving the second equation of (2), u = θx, T =θ z we rewrite (1) in the form 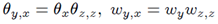 In[3] it was shown that the solution of the symmetry equation T, may be obtained in terms of αn functions which satisfy the following recurrence relations
In[3] it was shown that the solution of the symmetry equation T, may be obtained in terms of αn functions which satisfy the following recurrence relations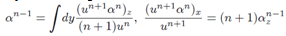 Eliminating αn-1 from both equations we arrive at the equation for the functions αn in the form
Eliminating αn-1 from both equations we arrive at the equation for the functions αn in the form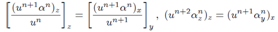 The left and right equations are the same. From these expressions it follows that there exists an obvious solution αn = 1 which leads to a finite solution for T. The solution for T becomes
The left and right equations are the same. From these expressions it follows that there exists an obvious solution αn = 1 which leads to a finite solution for T. The solution for T becomes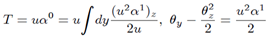 | (5) |
The second equality is obtained from the first one after the substitutionT=θz, u= θx and differentiation of the subsequent expression 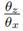 with respect to the argument y and integration once over z
with respect to the argument y and integration once over z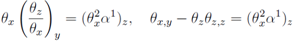 The last equality is a series of additional conditions on the θx,y = θx θz,z for the function θ.
The last equality is a series of additional conditions on the θx,y = θx θz,z for the function θ.
3. Generalization of R. Ward's Solution
This section explains why the analytic solutions of Ward exist at all. The simplest solution of the symmetry equation is a linear combination of derivatives of the functions u S = wy = uz = aux + buy + cuz. The solution of Richard Ward corresponds to choosing c = 1, a =- b. In the case c is not equal to zero we have uz = Aux + Buy and the second system under this additional condition becomes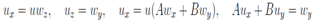 Let us seek a solution of this system in the form
Let us seek a solution of this system in the form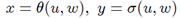 The system of equations defining derivatives of (u, w) with respect to space coordinates (x, y) is the following one;
The system of equations defining derivatives of (u, w) with respect to space coordinates (x, y) is the following one;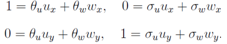 After solving the last system,
After solving the last system,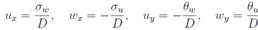 and substitution into the previous one we arrive at a linear system of equations for θ (u, w) and σ(u, w).
and substitution into the previous one we arrive at a linear system of equations for θ (u, w) and σ(u, w).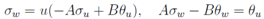 The last system after eliminating (for instance) the function σ leads to an equation of the second order with separable variables
The last system after eliminating (for instance) the function σ leads to an equation of the second order with separable variables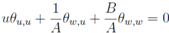
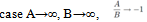
4. The Zero Order Term of Series Solution to the Symmetry Equation
In the case α0 = 1 from the general formula it follows that T = u or w = u and from the corresponding formulas of the previous section we obtain ux = uz or uy = uz. These are particular cases of the generalized Ward construction of the previous section. The first equations in this case lead uy = uuz. This is the well known Monge equation (the equation of Hamilton-Jacobi for free motion in one dimension) with general solution z + y + ux = F (u) or z + x + uy = F (u). It is not difficult to connect these solutions with the generalized Ward solution of the previous section.
5. The First Term of the Symmetry Equation Series Solution
In this case α1 = 1. It is possible represent the solution of the symmetry equation in different variables and in connection of this it will possible to obtain two different solutions (at least known to us) of the continuous Toda chain.
5.1. The First Possibility
In connection with the recurrence procedure we obtain 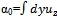 and the solution for T takes the form
and the solution for T takes the form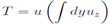 or after passing to the function θ, u=θx, T= θz, (obeying the equation θy,x= θxθz,z) it appears as
or after passing to the function θ, u=θx, T= θz, (obeying the equation θy,x= θxθz,z) it appears as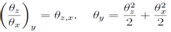 In the transformation from the left to the right hand sides we have used the equation for θ and the once integrated result on z. From the second form of the equation above it follows that θ is a solution of the Monge-Ampere equation of the third order and it is possible to use its known general solution. We will go by more direct way (which is obviously equivalent to the previous one). Now let us introduce the notations
In the transformation from the left to the right hand sides we have used the equation for θ and the once integrated result on z. From the second form of the equation above it follows that θ is a solution of the Monge-Ampere equation of the third order and it is possible to use its known general solution. We will go by more direct way (which is obviously equivalent to the previous one). Now let us introduce the notations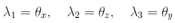 After differentiation on the right hand equation by x and z respectively and taking into account the above definition of λ we arrive at the system of equations
After differentiation on the right hand equation by x and z respectively and taking into account the above definition of λ we arrive at the system of equations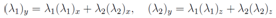 The last system is well known and its general solution in implicit form is the following:[7]
The last system is well known and its general solution in implicit form is the following:[7]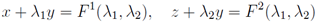 where F 1, F 2 are arbitrary functions of their two arguments. But in our case we have additional conditions (λ1)z = (λ2)x and this fact will limit the functions F 1, F 2. After differentiation of the two equations by x, z, y respectively and solving a linear system of algebraic equations we obtain all derivatives of the functions (λ1, λ2) with respect to these three arguments. The result is the following:
where F 1, F 2 are arbitrary functions of their two arguments. But in our case we have additional conditions (λ1)z = (λ2)x and this fact will limit the functions F 1, F 2. After differentiation of the two equations by x, z, y respectively and solving a linear system of algebraic equations we obtain all derivatives of the functions (λ1, λ2) with respect to these three arguments. The result is the following: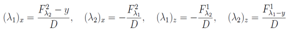 | (6) |
where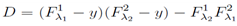 | (7) |
is the determinant of linear system under consideration. From the additional condition above and calculated values of corresponding derivatives of the function λ we obtained in the last equation we have F 1 = Gλ1 ; F 2 = G λ2. In the same way we obtain for derivatives of the functions with respect the argument y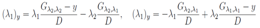 The last calculations show that the implicitly defined functions from the equations above satisfy the necessary system of equations and allow us to obtain a further constraint on the function G which arises from the fact that the equation for the function θ must be satisfied.. Namely
The last calculations show that the implicitly defined functions from the equations above satisfy the necessary system of equations and allow us to obtain a further constraint on the function G which arises from the fact that the equation for the function θ must be satisfied.. Namely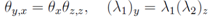 After substitution in the last equation of all expressions obtained above we pass to
After substitution in the last equation of all expressions obtained above we pass to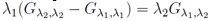 After the introduction of new variables s=λ1 λ2,
After the introduction of new variables s=λ1 λ2, 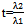 the last equations lead to a two dimensional equation with separable variables. Indeed
the last equations lead to a two dimensional equation with separable variables. Indeed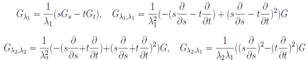 Substituting these expressions into equation for G we seek its solution in the form
Substituting these expressions into equation for G we seek its solution in the form 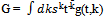 and pass to
and pass to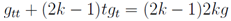 Thus for the function G we obtain finally
Thus for the function G we obtain finally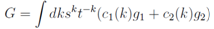 where c1, c2 are arbitrary functions of argument k and g1, g2 are two fundamental solutions of the linear equation of second order above. Thus for the solution of the Toda chain u =θx =λ1 we obtain an implicit solution for it
where c1, c2 are arbitrary functions of argument k and g1, g2 are two fundamental solutions of the linear equation of second order above. Thus for the solution of the Toda chain u =θx =λ1 we obtain an implicit solution for it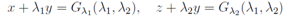 where G is the general solution of the linear equation above containing two arbitrary functions.
where G is the general solution of the linear equation above containing two arbitrary functions.
5.1.1. An example
By direct calculations it is not difficult to check that G =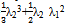 is a partial solution of equation of the subsection above. Thus in connection of the main result
is a partial solution of equation of the subsection above. Thus in connection of the main result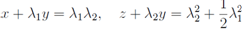 and λ1 = u is a solution of the continuous Toda chain. Eliminating λ2 from the equations above we obtain for u
and λ1 = u is a solution of the continuous Toda chain. Eliminating λ2 from the equations above we obtain for u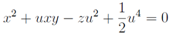 Calculation of necessary derivatives
Calculation of necessary derivatives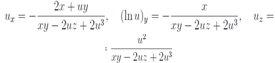
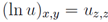
5.2. The Second Possibility
In the case α1 =1 in connection with the recurrence procedure we obtain 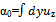 and the solution for T takes the form
and the solution for T takes the form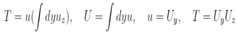 and the equations which are necessary to solve are the following;
and the equations which are necessary to solve are the following;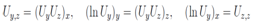 The first and the last equations above lead to a relation between the derivatives (after integration once with respect to the argument z) in the form ln
The first and the last equations above lead to a relation between the derivatives (after integration once with respect to the argument z) in the form ln 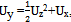 ,.
,. 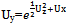 As in the previous subsection it means that U is a solution of the Monge-Ampere equation of the third order. It is possible to substitute its general solution into the last equation and find some restrictions to determine the arbitrary functions in the solution. We will go more directly.Let us seek a solution of these equations using the following parameterization
As in the previous subsection it means that U is a solution of the Monge-Ampere equation of the third order. It is possible to substitute its general solution into the last equation and find some restrictions to determine the arbitrary functions in the solution. We will go more directly.Let us seek a solution of these equations using the following parameterization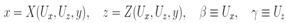 from which expressions for second order derivatives follow immediately;
from which expressions for second order derivatives follow immediately;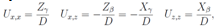 X = Wβ (β, γ, y); Z = Wγ (β, γ, y) and the equation transform to a linear equation of second order with separable variables
X = Wβ (β, γ, y); Z = Wγ (β, γ, y) and the equation transform to a linear equation of second order with separable variables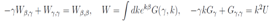 It is possible determine the dependence of the function W upon its argument after solution of two equations which arise after differentiation of the previous equations by the argument y
It is possible determine the dependence of the function W upon its argument after solution of two equations which arise after differentiation of the previous equations by the argument y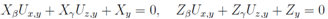 Remembering that
Remembering that 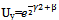 after trivial manipulations we rewrite the last equations in a form
after trivial manipulations we rewrite the last equations in a form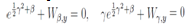 we obtain for W and explicit expressions for x,z
we obtain for W and explicit expressions for x,z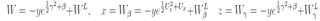 where W L is solution of the linear equation obtained above, which do not depend on argument y. The solution of the Toda chain of the beginning of this paper is given by connection
where W L is solution of the linear equation obtained above, which do not depend on argument y. The solution of the Toda chain of the beginning of this paper is given by connection 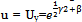 and dependence β, γ functions on independent arguments x, z, y is defined in explicit form by formulas above.
and dependence β, γ functions on independent arguments x, z, y is defined in explicit form by formulas above.
5.3 Second Example
This example may help the reader to understand the difficulties in trying to obtain solutions in explicit form. It is easy to check that W L =γ e-β is an explicit solution of the linear equation and thus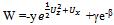 . The implicit form of the solution is given by
. The implicit form of the solution is given by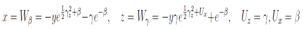 From these expressions the equation
From these expressions the equation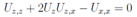 follows immediately. It is equivalent to our linear system above. With the help of this equation it is not difficult to check that
follows immediately. It is equivalent to our linear system above. With the help of this equation it is not difficult to check that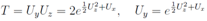 satisfy the equations
satisfy the equations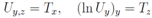 We rewrite equations which define an implicit solution in a form u =
We rewrite equations which define an implicit solution in a form u =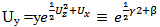 in equivalent form
in equivalent form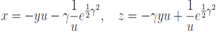 After eliminating terms without y on the right hand side we arrive at a quadratic equation to determinate the variable γ
After eliminating terms without y on the right hand side we arrive at a quadratic equation to determinate the variable γ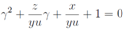 Substituting the solution of this equation into the first or second equations we reach an equation determining in implicit form the function u. It is obvious that to obtain this equation is not a very simple problem.
Substituting the solution of this equation into the first or second equations we reach an equation determining in implicit form the function u. It is obvious that to obtain this equation is not a very simple problem.
6. Second Step
In the case where α2 = 1 in connection with the recurrence procedure we obtain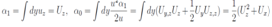 and the solution for T takes the form
and the solution for T takes the form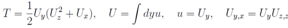 | (8) |
The equations which are necessary to solve are the following;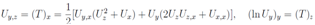 Let us introduce the definitions
Let us introduce the definitions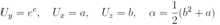 Equations above together with the notation introduced lead to the following system of equations
Equations above together with the notation introduced lead to the following system of equations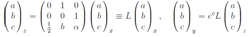 As in the cases above we will seek solution of these equation by implicit substitution
As in the cases above we will seek solution of these equation by implicit substitution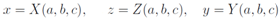 After differentiation of these equalities with respect to the independent arguments of the problem and introduction of the matrix
After differentiation of these equalities with respect to the independent arguments of the problem and introduction of the matrix 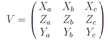 we have
we have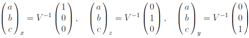 Substituting these expressions in linear system equations of the first order we obtain
Substituting these expressions in linear system equations of the first order we obtain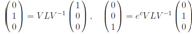 The last equations allow us to reconstruct the explicit form matrix V LV-1
The last equations allow us to reconstruct the explicit form matrix V LV-1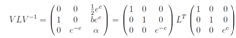 The first two columns are a direct consequence of the equations above. The last column arises from the fact Trace(V LV-1)n = Trace Ln.Now we arrive at a linear system of equations for determining the functions X, Z, Y.
The first two columns are a direct consequence of the equations above. The last column arises from the fact Trace(V LV-1)n = Trace Ln.Now we arrive at a linear system of equations for determining the functions X, Z, Y.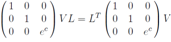
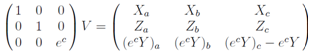 ecY we will denote by Y. A system of 9 equations follows;
ecY we will denote by Y. A system of 9 equations follows;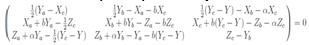 Elements M1,1 and M3,3 lead to a parametrization X = Ra, Y = Rc, Z = Rb + f(a,b). Elements M2,1 and M1,2 both lead to equation (Ra + bRc)a =
Elements M1,1 and M3,3 lead to a parametrization X = Ra, Y = Rc, Z = Rb + f(a,b). Elements M2,1 and M1,2 both lead to equation (Ra + bRc)a = 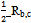 Element M2,2 allows us to conclude that the function f depends only from one argument b. Elements M3,1 and M1,3 are the sane and lead to equation (Rb + Rc)a = 12 Rc,c. And finally elements M3,2 and M2,3 pass to a third equation in the form (Rb + f(b) + Rc)b = (Ra + bRc)c. Thus we have three equations which it is necessary solve
Element M2,2 allows us to conclude that the function f depends only from one argument b. Elements M3,1 and M1,3 are the sane and lead to equation (Rb + Rc)a = 12 Rc,c. And finally elements M3,2 and M2,3 pass to a third equation in the form (Rb + f(b) + Rc)b = (Ra + bRc)c. Thus we have three equations which it is necessary solve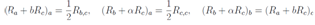 For further calculations the variables b,
For further calculations the variables b, 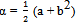 , c will be more suitable. In these variables the system equations above appears as
, c will be more suitable. In these variables the system equations above appears as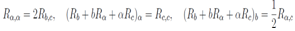 These equations can be interpreted as the vanishing of the curl of some vector which means that vector by itself is gradient of some scalar function, or and that the same system of equations of the second order above can be rewritten as the system of equation of the first order for two unknown functions R, Q
These equations can be interpreted as the vanishing of the curl of some vector which means that vector by itself is gradient of some scalar function, or and that the same system of equations of the second order above can be rewritten as the system of equation of the first order for two unknown functions R, Q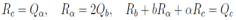 Eliminating Q we come back to equations for R. Eliminating R, we pass to a system of equations for Q in the form
Eliminating Q we come back to equations for R. Eliminating R, we pass to a system of equations for Q in the form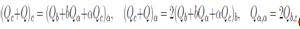 | (9) |
The last is the usual Laplace equation in three dimensions, which is invariant with respect to transformations of the five dimensional rotation group. One is operators of which is exactly 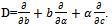 The last equation is a consequence of the two first ones. From them it follows that (DQ)α,α = 2(DQ)b,c and operator D commutes with the Laplace operator. Thus the last equation above is consequence of two first ones. Let us seek a solution the last system of equations in the form of Laplace-Fourier transform.
The last equation is a consequence of the two first ones. From them it follows that (DQ)α,α = 2(DQ)b,c and operator D commutes with the Laplace operator. Thus the last equation above is consequence of two first ones. Let us seek a solution the last system of equations in the form of Laplace-Fourier transform.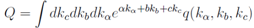 After substituting this into the system of equations above under the sign of integral we obtain two equations
After substituting this into the system of equations above under the sign of integral we obtain two equations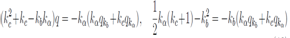 | (10) |
Eliminating terms with derivatives we arrive at a condition of self consistency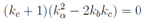 The first possibility kc +1 = 0 we call the degenerate solution the second one non degenerate one.
The first possibility kc +1 = 0 we call the degenerate solution the second one non degenerate one.
6.1. Degenerate Case
Let us seek solution Q of Laplace equation under additional condition DQ = 0. In this case simultaneously Qc + Q = f(b) or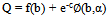 . Now
. Now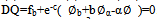 . The solution of the last equation is
. The solution of the last equation is 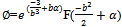 and finally the degenerate solution of the problem is
and finally the degenerate solution of the problem is 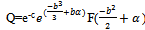 . But in this case the third equation is no more a consequence of two first ones and it must be satisfied independently. We have
. But in this case the third equation is no more a consequence of two first ones and it must be satisfied independently. We have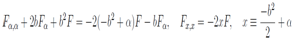 This ordinary differential equation may be solved in terms of Bessel functions. Coming back to the function R we obtain
This ordinary differential equation may be solved in terms of Bessel functions. Coming back to the function R we obtain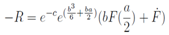 By direct calculations it is simple to check that all equations for R above are satisfied. A solution of the continuous Toda chain u = e-c in implicit form is determined from the equations
By direct calculations it is simple to check that all equations for R above are satisfied. A solution of the continuous Toda chain u = e-c in implicit form is determined from the equations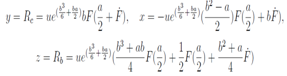
6.2. Non Degenerate Case
In this case 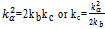 The first equation of (10) is rewritten in the form
The first equation of (10) is rewritten in the form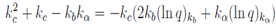 The solution the last equation of the first order is
The solution the last equation of the first order is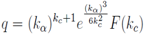 where F is a scalar function of its argument. Finally we obtain
where F is a scalar function of its argument. Finally we obtain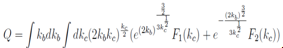 | (11) |
The first equation gives R = Qα, W = Qc. Substituting into both other equations we pass to a system of two equations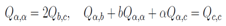 Let us seek a solution of this linear system above by a Laplace-Fourier trans-form
Let us seek a solution of this linear system above by a Laplace-Fourier trans-form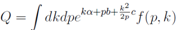 The first equation is satisfied automatically. The second one leads to a differential equation of the first order in partial derivatives for the determination of the function f(k, p) under the integral sign, which for the function
The first equation is satisfied automatically. The second one leads to a differential equation of the first order in partial derivatives for the determination of the function f(k, p) under the integral sign, which for the function  f is
f is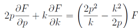 with the obvious solution
with the obvious solution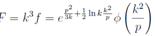 | (12) |
where 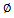 is an arbitrary function of the argument
is an arbitrary function of the argument 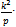
7. Conclusions
We have presented a new idea, unknown up to now to the best of our knowledge in the theory of integrable systems connected with the symmetry equation of the initial system. We have also presented some non-trivial solutions of the 2 + 1 continuous Toda chain. These solutions are often only given in implicit form. An explicit solution is however obtained as a specific example. It may be that this is the best that can be hoped for, i.e. that in the general case the solution is only obtainable in implicit form. This is the case for many non-linear systems, including that of the simple non-linear wave (Monge) equation. The method of solution presented here is far from obvious or straightforward. We hope that a more direct method of finding a solution can be found; now we know that a solution is possible
References
| [1] | J.F. Plebanski J. Math. Phys 16, pp. 2395, 1975. |
| [2] | C. Boyer, D. Finley J. Math. Phys 23, pp. 1126-1130, 1982. |
| [3] | D. B .Fairlie, A. N. Leznov Phys. Lett. A 16, pp. 2395, 1996 |
| [4] | C. Boyer, D. Finley J. Math. Phys 23, pp. 1126-1130, 1982. |
| [5] | A.N.. Leznov To the question of the integration of Plebansky Equation, arXiv: 0903.4440, 2009. |
| [6] | L.V. Ovsjanikov Group Analysis of differential equations, Acad. Press New-York, 1992. |
| [7] | D.B.Fairlie and A.N. Leznov, General solutions of the Monge-Ampere equation in n-dimensional space Journal of Geometry and Physics. 16, pp. 385-390, 1995. |
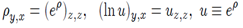
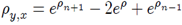 under appropriate rescaling (n→z). The series solutions of the symmetry equation for the Toda chain was found in[3].Also, a solution of the two dimensional reduction of (1) (ρ = (z, y + x) was found in implicit form in[4]. Infinite series solutions of the symmetry equation corresponding to (1) were found in[5]. But the connection between series solutions of the symmetry equation with the solution of the initial system (1) has not been discovered. However general theory gives a guarantee that each solution of symmetry equation is connected with an analytical solution of the initial system in explicit or implicit form. The goal of the present paper is to fill this gap and demonstrate a way how an analytical solution of (1) is connected with the solution constructed in[3] of the symmetry equation. In[5], thePlebansky equation was represented in the form of two equations of the first order for two unknown functions, one of which satisfies the Plebansky equation by itself, the second one satisfies the corresponding symmetry equation. It is possible to find in an independent way the solution of symmetry equation in recurrence form. As was remarked the above equation under consideration in the present paper is a reduction of the Plebansky equation and so it is possible to try to solve it by the same methods[6].
under appropriate rescaling (n→z). The series solutions of the symmetry equation for the Toda chain was found in[3].Also, a solution of the two dimensional reduction of (1) (ρ = (z, y + x) was found in implicit form in[4]. Infinite series solutions of the symmetry equation corresponding to (1) were found in[5]. But the connection between series solutions of the symmetry equation with the solution of the initial system (1) has not been discovered. However general theory gives a guarantee that each solution of symmetry equation is connected with an analytical solution of the initial system in explicit or implicit form. The goal of the present paper is to fill this gap and demonstrate a way how an analytical solution of (1) is connected with the solution constructed in[3] of the symmetry equation. In[5], thePlebansky equation was represented in the form of two equations of the first order for two unknown functions, one of which satisfies the Plebansky equation by itself, the second one satisfies the corresponding symmetry equation. It is possible to find in an independent way the solution of symmetry equation in recurrence form. As was remarked the above equation under consideration in the present paper is a reduction of the Plebansky equation and so it is possible to try to solve it by the same methods[6].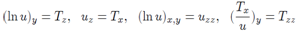
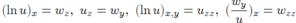
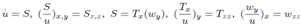 It is necessary to understand the last manipulation in such way, that if we represent the solution of the symmetry equation in the form S = Tx or S = wy then the last equations in (2), (3) are exactly the symmetry equation by itself. Finally a linear system of equations of first order for the function u function is
It is necessary to understand the last manipulation in such way, that if we represent the solution of the symmetry equation in the form S = Tx or S = wy then the last equations in (2), (3) are exactly the symmetry equation by itself. Finally a linear system of equations of first order for the function u function is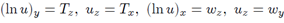
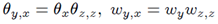 In[3] it was shown that the solution of the symmetry equation T, may be obtained in terms of αn functions which satisfy the following recurrence relations
In[3] it was shown that the solution of the symmetry equation T, may be obtained in terms of αn functions which satisfy the following recurrence relations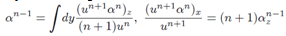 Eliminating αn-1 from both equations we arrive at the equation for the functions αn in the form
Eliminating αn-1 from both equations we arrive at the equation for the functions αn in the form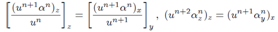 The left and right equations are the same. From these expressions it follows that there exists an obvious solution αn = 1 which leads to a finite solution for T. The solution for T becomes
The left and right equations are the same. From these expressions it follows that there exists an obvious solution αn = 1 which leads to a finite solution for T. The solution for T becomes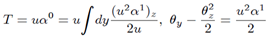
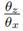 with respect to the argument y and integration once over z
with respect to the argument y and integration once over z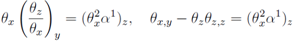 The last equality is a series of additional conditions on the θx,y = θx θz,z for the function θ.
The last equality is a series of additional conditions on the θx,y = θx θz,z for the function θ.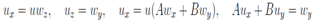 Let us seek a solution of this system in the form
Let us seek a solution of this system in the form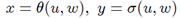 The system of equations defining derivatives of (u, w) with respect to space coordinates (x, y) is the following one;
The system of equations defining derivatives of (u, w) with respect to space coordinates (x, y) is the following one;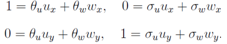 After solving the last system,
After solving the last system,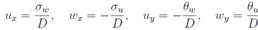 and substitution into the previous one we arrive at a linear system of equations for θ (u, w) and σ(u, w).
and substitution into the previous one we arrive at a linear system of equations for θ (u, w) and σ(u, w).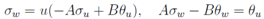 The last system after eliminating (for instance) the function σ leads to an equation of the second order with separable variables
The last system after eliminating (for instance) the function σ leads to an equation of the second order with separable variables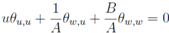
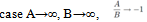
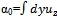 and the solution for T takes the form
and the solution for T takes the form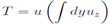 or after passing to the function θ, u=θx, T= θz, (obeying the equation θy,x= θxθz,z) it appears as
or after passing to the function θ, u=θx, T= θz, (obeying the equation θy,x= θxθz,z) it appears as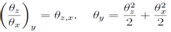 In the transformation from the left to the right hand sides we have used the equation for θ and the once integrated result on z. From the second form of the equation above it follows that θ is a solution of the Monge-Ampere equation of the third order and it is possible to use its known general solution. We will go by more direct way (which is obviously equivalent to the previous one). Now let us introduce the notations
In the transformation from the left to the right hand sides we have used the equation for θ and the once integrated result on z. From the second form of the equation above it follows that θ is a solution of the Monge-Ampere equation of the third order and it is possible to use its known general solution. We will go by more direct way (which is obviously equivalent to the previous one). Now let us introduce the notations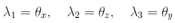 After differentiation on the right hand equation by x and z respectively and taking into account the above definition of λ we arrive at the system of equations
After differentiation on the right hand equation by x and z respectively and taking into account the above definition of λ we arrive at the system of equations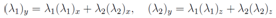 The last system is well known and its general solution in implicit form is the following:[7]
The last system is well known and its general solution in implicit form is the following:[7]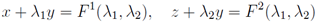 where F 1, F 2 are arbitrary functions of their two arguments. But in our case we have additional conditions (λ1)z = (λ2)x and this fact will limit the functions F 1, F 2. After differentiation of the two equations by x, z, y respectively and solving a linear system of algebraic equations we obtain all derivatives of the functions (λ1, λ2) with respect to these three arguments. The result is the following:
where F 1, F 2 are arbitrary functions of their two arguments. But in our case we have additional conditions (λ1)z = (λ2)x and this fact will limit the functions F 1, F 2. After differentiation of the two equations by x, z, y respectively and solving a linear system of algebraic equations we obtain all derivatives of the functions (λ1, λ2) with respect to these three arguments. The result is the following: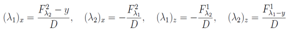
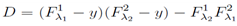
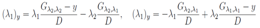 The last calculations show that the implicitly defined functions from the equations above satisfy the necessary system of equations and allow us to obtain a further constraint on the function G which arises from the fact that the equation for the function θ must be satisfied.. Namely
The last calculations show that the implicitly defined functions from the equations above satisfy the necessary system of equations and allow us to obtain a further constraint on the function G which arises from the fact that the equation for the function θ must be satisfied.. Namely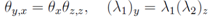 After substitution in the last equation of all expressions obtained above we pass to
After substitution in the last equation of all expressions obtained above we pass to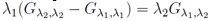 After the introduction of new variables s=λ1 λ2,
After the introduction of new variables s=λ1 λ2, 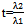 the last equations lead to a two dimensional equation with separable variables. Indeed
the last equations lead to a two dimensional equation with separable variables. Indeed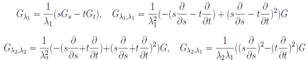 Substituting these expressions into equation for G we seek its solution in the form
Substituting these expressions into equation for G we seek its solution in the form 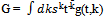 and pass to
and pass to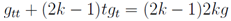 Thus for the function G we obtain finally
Thus for the function G we obtain finally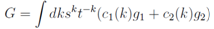 where c1, c2 are arbitrary functions of argument k and g1, g2 are two fundamental solutions of the linear equation of second order above. Thus for the solution of the Toda chain u =θx =λ1 we obtain an implicit solution for it
where c1, c2 are arbitrary functions of argument k and g1, g2 are two fundamental solutions of the linear equation of second order above. Thus for the solution of the Toda chain u =θx =λ1 we obtain an implicit solution for it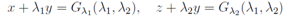 where G is the general solution of the linear equation above containing two arbitrary functions.
where G is the general solution of the linear equation above containing two arbitrary functions.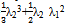 is a partial solution of equation of the subsection above. Thus in connection of the main result
is a partial solution of equation of the subsection above. Thus in connection of the main result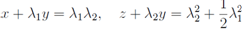 and λ1 = u is a solution of the continuous Toda chain. Eliminating λ2 from the equations above we obtain for u
and λ1 = u is a solution of the continuous Toda chain. Eliminating λ2 from the equations above we obtain for u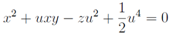 Calculation of necessary derivatives
Calculation of necessary derivatives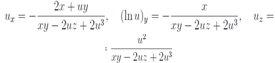
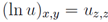
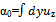 and the solution for T takes the form
and the solution for T takes the form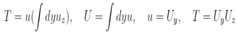 and the equations which are necessary to solve are the following;
and the equations which are necessary to solve are the following;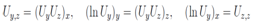 The first and the last equations above lead to a relation between the derivatives (after integration once with respect to the argument z) in the form ln
The first and the last equations above lead to a relation between the derivatives (after integration once with respect to the argument z) in the form ln 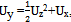 ,.
,. 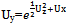 As in the previous subsection it means that U is a solution of the Monge-Ampere equation of the third order. It is possible to substitute its general solution into the last equation and find some restrictions to determine the arbitrary functions in the solution. We will go more directly.Let us seek a solution of these equations using the following parameterization
As in the previous subsection it means that U is a solution of the Monge-Ampere equation of the third order. It is possible to substitute its general solution into the last equation and find some restrictions to determine the arbitrary functions in the solution. We will go more directly.Let us seek a solution of these equations using the following parameterization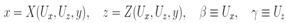 from which expressions for second order derivatives follow immediately;
from which expressions for second order derivatives follow immediately;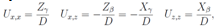 X = Wβ (β, γ, y); Z = Wγ (β, γ, y) and the equation transform to a linear equation of second order with separable variables
X = Wβ (β, γ, y); Z = Wγ (β, γ, y) and the equation transform to a linear equation of second order with separable variables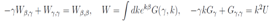 It is possible determine the dependence of the function W upon its argument after solution of two equations which arise after differentiation of the previous equations by the argument y
It is possible determine the dependence of the function W upon its argument after solution of two equations which arise after differentiation of the previous equations by the argument y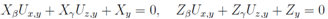 Remembering that
Remembering that 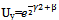 after trivial manipulations we rewrite the last equations in a form
after trivial manipulations we rewrite the last equations in a form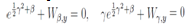 we obtain for W and explicit expressions for x,z
we obtain for W and explicit expressions for x,z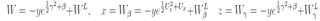 where W L is solution of the linear equation obtained above, which do not depend on argument y. The solution of the Toda chain of the beginning of this paper is given by connection
where W L is solution of the linear equation obtained above, which do not depend on argument y. The solution of the Toda chain of the beginning of this paper is given by connection 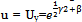 and dependence β, γ functions on independent arguments x, z, y is defined in explicit form by formulas above.
and dependence β, γ functions on independent arguments x, z, y is defined in explicit form by formulas above.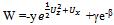 . The implicit form of the solution is given by
. The implicit form of the solution is given by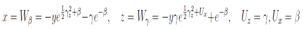 From these expressions the equation
From these expressions the equation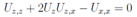 follows immediately. It is equivalent to our linear system above. With the help of this equation it is not difficult to check that
follows immediately. It is equivalent to our linear system above. With the help of this equation it is not difficult to check that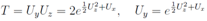 satisfy the equations
satisfy the equations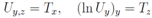 We rewrite equations which define an implicit solution in a form u =
We rewrite equations which define an implicit solution in a form u =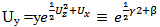 in equivalent form
in equivalent form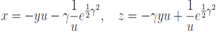 After eliminating terms without y on the right hand side we arrive at a quadratic equation to determinate the variable γ
After eliminating terms without y on the right hand side we arrive at a quadratic equation to determinate the variable γ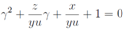 Substituting the solution of this equation into the first or second equations we reach an equation determining in implicit form the function u. It is obvious that to obtain this equation is not a very simple problem.
Substituting the solution of this equation into the first or second equations we reach an equation determining in implicit form the function u. It is obvious that to obtain this equation is not a very simple problem.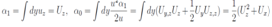 and the solution for T takes the form
and the solution for T takes the form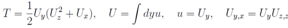
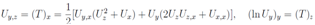 Let us introduce the definitions
Let us introduce the definitions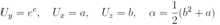 Equations above together with the notation introduced lead to the following system of equations
Equations above together with the notation introduced lead to the following system of equations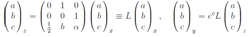 As in the cases above we will seek solution of these equation by implicit substitution
As in the cases above we will seek solution of these equation by implicit substitution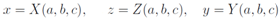 After differentiation of these equalities with respect to the independent arguments of the problem and introduction of the matrix
After differentiation of these equalities with respect to the independent arguments of the problem and introduction of the matrix 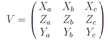 we have
we have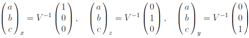 Substituting these expressions in linear system equations of the first order we obtain
Substituting these expressions in linear system equations of the first order we obtain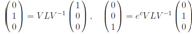 The last equations allow us to reconstruct the explicit form matrix V LV-1
The last equations allow us to reconstruct the explicit form matrix V LV-1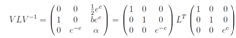 The first two columns are a direct consequence of the equations above. The last column arises from the fact Trace(V LV-1)n = Trace Ln.Now we arrive at a linear system of equations for determining the functions X, Z, Y.
The first two columns are a direct consequence of the equations above. The last column arises from the fact Trace(V LV-1)n = Trace Ln.Now we arrive at a linear system of equations for determining the functions X, Z, Y.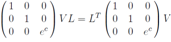
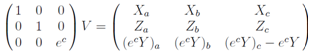 ecY we will denote by Y. A system of 9 equations follows;
ecY we will denote by Y. A system of 9 equations follows;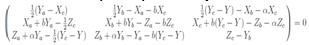 Elements M1,1 and M3,3 lead to a parametrization X = Ra, Y = Rc, Z = Rb + f(a,b). Elements M2,1 and M1,2 both lead to equation (Ra + bRc)a =
Elements M1,1 and M3,3 lead to a parametrization X = Ra, Y = Rc, Z = Rb + f(a,b). Elements M2,1 and M1,2 both lead to equation (Ra + bRc)a = 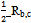 Element M2,2 allows us to conclude that the function f depends only from one argument b. Elements M3,1 and M1,3 are the sane and lead to equation (Rb + Rc)a = 12 Rc,c. And finally elements M3,2 and M2,3 pass to a third equation in the form (Rb + f(b) + Rc)b = (Ra + bRc)c. Thus we have three equations which it is necessary solve
Element M2,2 allows us to conclude that the function f depends only from one argument b. Elements M3,1 and M1,3 are the sane and lead to equation (Rb + Rc)a = 12 Rc,c. And finally elements M3,2 and M2,3 pass to a third equation in the form (Rb + f(b) + Rc)b = (Ra + bRc)c. Thus we have three equations which it is necessary solve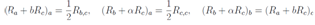 For further calculations the variables b,
For further calculations the variables b, 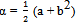 , c will be more suitable. In these variables the system equations above appears as
, c will be more suitable. In these variables the system equations above appears as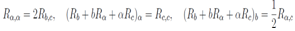 These equations can be interpreted as the vanishing of the curl of some vector which means that vector by itself is gradient of some scalar function, or and that the same system of equations of the second order above can be rewritten as the system of equation of the first order for two unknown functions R, Q
These equations can be interpreted as the vanishing of the curl of some vector which means that vector by itself is gradient of some scalar function, or and that the same system of equations of the second order above can be rewritten as the system of equation of the first order for two unknown functions R, Q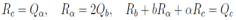 Eliminating Q we come back to equations for R. Eliminating R, we pass to a system of equations for Q in the form
Eliminating Q we come back to equations for R. Eliminating R, we pass to a system of equations for Q in the form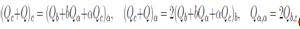
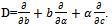 The last equation is a consequence of the two first ones. From them it follows that (DQ)α,α = 2(DQ)b,c and operator D commutes with the Laplace operator. Thus the last equation above is consequence of two first ones. Let us seek a solution the last system of equations in the form of Laplace-Fourier transform.
The last equation is a consequence of the two first ones. From them it follows that (DQ)α,α = 2(DQ)b,c and operator D commutes with the Laplace operator. Thus the last equation above is consequence of two first ones. Let us seek a solution the last system of equations in the form of Laplace-Fourier transform.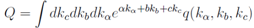 After substituting this into the system of equations above under the sign of integral we obtain two equations
After substituting this into the system of equations above under the sign of integral we obtain two equations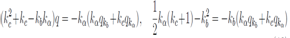
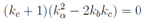 The first possibility kc +1 = 0 we call the degenerate solution the second one non degenerate one.
The first possibility kc +1 = 0 we call the degenerate solution the second one non degenerate one.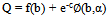 . Now
. Now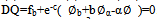 . The solution of the last equation is
. The solution of the last equation is 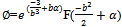 and finally the degenerate solution of the problem is
and finally the degenerate solution of the problem is 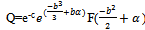 . But in this case the third equation is no more a consequence of two first ones and it must be satisfied independently. We have
. But in this case the third equation is no more a consequence of two first ones and it must be satisfied independently. We have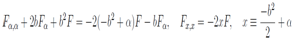 This ordinary differential equation may be solved in terms of Bessel functions. Coming back to the function R we obtain
This ordinary differential equation may be solved in terms of Bessel functions. Coming back to the function R we obtain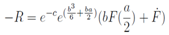 By direct calculations it is simple to check that all equations for R above are satisfied. A solution of the continuous Toda chain u = e-c in implicit form is determined from the equations
By direct calculations it is simple to check that all equations for R above are satisfied. A solution of the continuous Toda chain u = e-c in implicit form is determined from the equations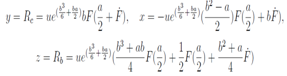
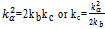 The first equation of (10) is rewritten in the form
The first equation of (10) is rewritten in the form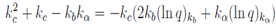 The solution the last equation of the first order is
The solution the last equation of the first order is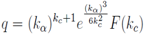 where F is a scalar function of its argument. Finally we obtain
where F is a scalar function of its argument. Finally we obtain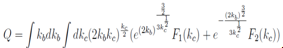
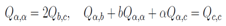 Let us seek a solution of this linear system above by a Laplace-Fourier trans-form
Let us seek a solution of this linear system above by a Laplace-Fourier trans-form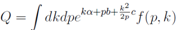 The first equation is satisfied automatically. The second one leads to a differential equation of the first order in partial derivatives for the determination of the function f(k, p) under the integral sign, which for the function
The first equation is satisfied automatically. The second one leads to a differential equation of the first order in partial derivatives for the determination of the function f(k, p) under the integral sign, which for the function 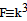 f is
f is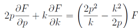 with the obvious solution
with the obvious solution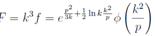
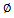 is an arbitrary function of the argument
is an arbitrary function of the argument 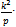
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML