Hesham M. M. Mansour 1, Khaled S. A. Hassaneen 2, 3
1Department of Physics, Faculty of Science, Cairo University, Giza, Egypt
2Department of Physics, Faculty of Science, Sohag University, Sohag, Egypt
3Department of Physics, Faculty of Science, Taif University, Taif, Saudi Arabia
Correspondence to: Khaled S. A. Hassaneen , Department of Physics, Faculty of Science, Sohag University, Sohag, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Results of cold and hot symmetric nuclear matter and pure neutron matter calculations are presented. The Brueckner-Hartree-Fock (BHF) approximation + two body density dependent Skyrme potential which is equivalent to three body interaction are used. Various modern nucleon-nucleon (NN) potentials are used in the framework of BHF approximation, e.g.: CD-Bonn potential, Nijm1 potential, Reid 93 potential and Argonne V18 potential. The bulk properties of asymmetric nuclear matter are computed such as the equation of state (EOS) at (T = 0), pressure at (T = 0, 5 and 10 MeV), single particle potential, free energy at (T = 5 and 10 MeV), nuclear matter incompressibility and the symmetry energy. Also the bulk properties of pure neutron matter are computed such as the EOS at (T = 0), pressure at (T = 0, 3 and 6 MeV), single particle potential, free energy at (T = 3 and 6MeV). Good agreement is obtained in comparison with previous theoretical estimates and experimental data.
Keywords:
BHF Approximation, Symmetric Nuclear Matter and Pure Neutron Matter, Finite Temperature, Three-Body Forces
1. Introduction
Static properties of nuclear matter e.g., binding energy, symmetry energy, etc; can be determined by the equation of state (EOS). The EOS of nuclear matter has been of great interest in nuclear physics and astrophysics[1-3]. The interest in the equation of state of nuclear matter stems from different motivations and prospects. First, it appears as a theoretical challenge to the possibility of predicting, on the basis of the meson theory of nucleon-nucleon interaction, the EOS of nuclear matter in the density range of up to a few times the saturation density (central density of heavy nuclei).At least three main areas of research, where phenomenological data can be obtained, have to be mentioned:(1) The data on medium and heavy nuclei. The mass formula which fits the smooth part of the binding energy of nuclei throughout the nuclear mass table allows extracting some general properties of the EOS. Similarly, the data on giant resonances can give an estimate of other bulk properties of nuclear matter, in particular the incompressibility.(2) The knowledge of the EOS in a wide range of density and asymmetry is the basis of any theory of neutron star structure and the prediction of their properties. The possible confrontations of the observable data with the theoretical predictions give a serious challenge to any theory of EOS. (3) Heavy ion collisions (HIC) at intermediate energies (20 < E /A < 200 MeV) give the possibility of compressing and heating pieces of nuclear matter.Few excellent review papers have been published[4] on this wide subject. Symmetric nuclear matter is defined to be an infinite system consisting of an equal number of protons Z and neutrons N, the Coulomb interaction is absent, and the number of particles A=N+Z approach infinity. The single-particle wave functions are taken to be plane waves. The nucleons occupy a volume Ω. For an infinite system, both A and Ω approach infinity, while the particle density ρ = A / Ω remains constant. The general quantum many-body theory is the subject of excellent textbooks[5,6]. The treatment is restricted to the Goldstone[7] and the Bethe-Brueckner-Goldstone (BBG) method[8,9]. If one considers the (BHFA) approximation which assumes that nucleons in nuclear matter move in a mean field arising from the interaction with all other nucleons one can reach a bound nuclear matter.The predictions of non-relativistic microscopic approaches (including both the BHF and variational approaches) based on pure two-body nucleon-nucleon (NN) forces (2BF) do not give the empirical saturation point of symmetric nuclear matter (Coester band.[10]). The medium effects are taken into account by phenomenological or microscopic three-body forces (3BF) within non-relativistic contexts. Calculations with phenomenological 3BF have been performed both in the framework of the variational approach[11,12] and the BHF approximation, [13-16].In this work the equation of state (EOS), pressure, etc are computed using different modern NN potentials like CD- Bonn[17], Argonne v18[18], Nijm1, and Reid 93[19] potentials in the framework of BHFA (conventional) choice plus a two body density dependent Skyrme potential which is equivalent to three body interaction. The conventional choice, assumes a single-particle potential U = 0 for single- particle states above the Fermi level, and approximate the energies by the kinetic energy only[20]. U is a self- consistent BHF potential for k < kF. We also computed the symmetry energy (ESym). The symmetry energy at high densities is very important in nuclear astrophysics for understanding e.g., the cooling mechanisms in a neutron star[21]. In the next section we give a brief description of the BHFA theory and the BGE. Section (3) is devoted to present the results of the calculation of the nuclear matter properties while in section (4) the results of the neutron matter are presented. A summary of the present work is given in section (5).
2. BHFA and BGE
The G-matrix is defined by: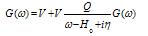 | (2.1) |
This is known as the Beth-Goldstone equation (BGE); for more details see Ref[22]; here ω is the starting energy which is usually the sum of the single particle energies of the states of the interacting nucleons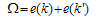 | (2.2) |
V is the bare NN potential, η is an infinitesimal small number, H is the unperturbed energy of the intermediate scattering states. Q is the Pauli projection operator, it projects out states with two nucleons above the Fermi level, and it is given by: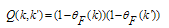 | (2.3) |
where ӨF (k) = 1 for k < kF and zero otherwise, ӨF (k) is the occupation probability of a free Fermi gas with a Fermi momentum kF. In the Brueckner-Goldstone expansion, the average binding energy per nucleon is expanded in a series of terms as follows: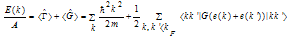 | (2.4) |
where |kk' > refers to antisymetrized two-body states. This first order is known as the Brueckner-Hartree-Fock approximation (BHFA). To completely determine the average binding energy one has to define the single particle potential U (k) which contributes to the single particle energies appearing in the G-matrix elements. The structure of the expression (2.4) suggests choosing the following BHF single particle potential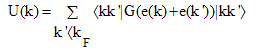 | (2.5) |
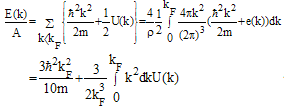 | (2.6) |
The G-matrix itself depends on U (k) through the starting energy ω, defined in Eq.(2.2) and the lowest order approximation (2.4) along with the choice (2.5) for the single particle potential. The single particle energy e (k) is defined as 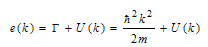 | (2.7) |
where Γ is the kinetic energy. In the conventional choice for the single particle potential one normally takes the BHF potential (eq. (2.5)) for the hole states (k < kF) and zero for particle states (k > kF),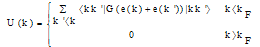 | (2.8) |
Thus introducing a large discontinuity in the single particle spectrum at the Fermi surface. However, due to the unphysical discontinuity at the Fermi surface, this auxiliary potential cannot be directly related to the average potential felt by a particle or a hole. Moreover, many other interesting properties can be derived such as the momentum distribution and the effective mass which is properly described using a continuous spectrum across the Fermi surface. This was the main motivation which led Mahaux and collaborators [23, 24] to introduce the continuous choice for the single particle potential thus treating particles and holes in a symmetrical way. The use of the continuous choice potential implies that the G-matrix elements needed in the self-consistent calculation are complex and the prescription advocated by Mahaux is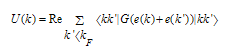 | (2.9) |
Eqs. (2.1) and (2.8) represent the main equations that one needs to solve self-consistently. In order to obtain such a self-consistent solution one often assumes a quadratic dependence of the single-particle energy on the momentum of the nucleon in the form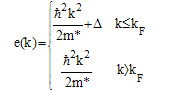 | (2.10) |
Where m* is the effective mass of the nucleon and ∆ is a constant. Starting with an appropriate choice for the parameters for the effective m* and the constant ∆, one can solve the Bethe-Goldstone equation and evaluate the single-particle energy[22]. The parameters m* and the constant ∆ can then be readjusted in such a way that the parameterization eq. (2.10) reproduces these two energies. This procedure is then iterated until a self-consistent solution is obtained. The parameterization of eq. (2.10), however, is useful not only to simplify the self-consistent solution of the BHF equations; but also leads to a simplification of the numerical solution of the Bethe-Goldstone equation.
3.1. EOS of the Symmetric Nuclear Matter at (T = 0)
The EOS is the relationship between energy per nucleon and Fermi momentum kF or density ρ, the minimum point of the curve is called the saturation point. In the present work one may introduce a Skyrme effective interaction density dependent term in addition to the BHF potential.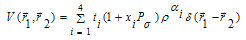 | (3.1) |
This is a two-body density dependent potential which is equivalent to three-body interaction. Where ti and xi are interaction parameters, Pσ is the spin exchange operator, ρ is the density, r1and r2 are the position vectors of the particle (1) and particle (2) respectively and αi = (1/3, 2/3, 1/2 and 1).The results are shown in the figure (3.1), where the energy per particle (E / A) in MeV is plotted against density ρ in fm-3, for symmetric nuclear matter using different potentials in comparison with Freidman and Pandharipande (F and P) [25].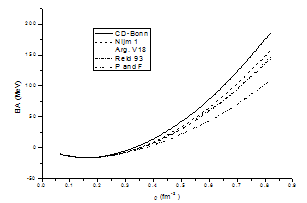 | Figure 3.1. E / A in MeV for symmetric nuclear matter at (T=0) as a function of density using different potentials for conventional choice in comparison with F and P[25] |
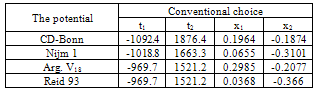
In Fig. (3.1) for conventional choice at T=0, the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared by F and P[25]. Good agreement is obtained for small values of kF around the minimum.Table 1. The saturation points as a function of Fermi momentum kF in terms of density ρ0 for various potentials
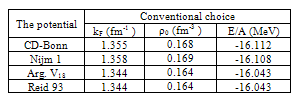 |
| |
|
Table (1) shows the saturation points for the different potentials as a function of Fermi momentum kF in (fm-1) in terms of the density ρ in (fm-3) for the conventional choice.
3.2. Pressure of the Symmetric Nuclear Matter at (T = 0)
The pressure for symmetric nuclear matter at T = 0 is defined in terms of the energy per particle as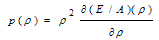 | (3.2) |
The results are shown in Fig. (3.2). The values of the pressure are plotted against the density ρ for symmetric nuclear matter for conventional choice using the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential in comparison with F and P[25]. From figure (3.2) it is observed that when the density of symmetric nuclear matter increases the pressure of nuclear matter increases.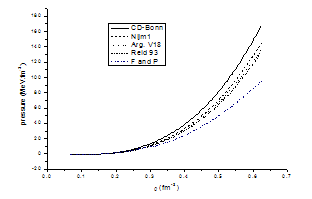 | Figure 3.2. The pressure of symmetric nuclear matter at (T = 0) as a function of density using different potentials for conventional choice in comparison with F and P[25] |
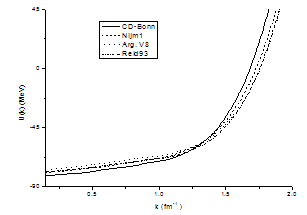 | Figure 3.3. The single particle potential for symmetric nuclear as a function of momentum k at (kF = 1.333 fm-1) for different potentials for conventional choice |
3.3. Single Particle Potential of the Symmetric Nuclear Matter
The single particle potential of e.g. a proton U is defined together with the kinetic energy as the energy required to remove this proton from the nuclear system leaving a hole in the state. The dependence of the single particle potential on the momentum k for symmetric nuclear matter at kF = 1.333 fm-1 for various potentials for conventional choice are shown in figure (3.3). The results for all potentials are similar in the conventional choice i.e. the single particle potential U increases with increasing the momentum k. There is another indication for the differences between the interactions considered: The local interactions Argonne V18 and Reid 93 are stiffer than the nonlocal CD-Bonn and Nijm 1 potentials. Therefore a larger part of the attraction in the effective interaction originates from the particle-particle ladder contributions to the G-matrix.
3.4. Free energy of the Symmetric Nuclear Matter at Different T
The free energy of nuclear mater is defined by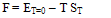 | (3.3) |
Where F is the free energy of the system, ET=0 is the total energy at T = 0, ST is the entropy of the system at temperature T and T is the temperature in (MeV).By using equation (3.3) the free energy[26] of the system at temperature T is defined by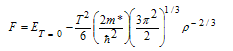 | (3.4) |
where m* is the effective mass of the nucleon at saturation. The free energy of nuclear matter in MeV is plotted against the density ρ in fm-3. The results are shown in the figures (3.4) and (3.5), for symmetric nuclear matter using different potentials in comparison with F and P[25].At T = 5 MeV, for conventional choice Fig. (3.4) the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared by F and P.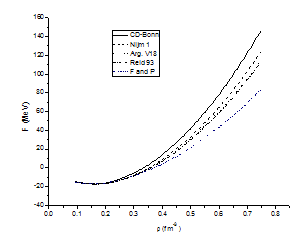 | Figure 3.4. The free energy at (T = 5 MeV) for symmetric nuclear matter as a function of density using different potentials for conventional choice compared by F and P[25] |
At T = 10 MeV, for conventional choice Fig. (3.5), the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared with F and P. From the plotted figures it is observed that the free energy first decreases with increasing the density until it reaches a minimum then it increases with increasing the density.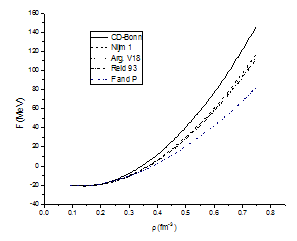 | Figure 3.5. The same as Fig. (3.4) but at T=10 MeV |
3.5. Pressure of the Symmetric Nuclear Matter at Different T
At (T = 5 and 10 MeV), the following equation is used for calculating the pressure of symmetric nuclear matter by using the T2-approximation[26]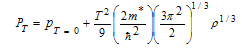 | (3.5) |
where m* is the effective mass of the nucleon.The results are shown in Fig. (3.6). The values of pressure at (T = 5 MeV) are plotted against the density ρ for symmetric nuclear matter for conventional choice, using the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared with F and P.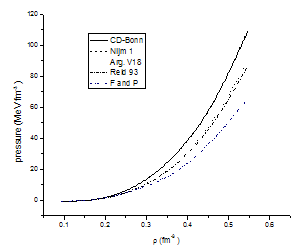 | Figure 3.6. The pressure for symmetric nuclear matter at (T = 5 MeV) as a function of density using different potentials for conventional choice compared by F and P [25] |
In Fig. (3.7), the values of pressure at (T = 10 MeV) are plotted against the density ρ for symmetric nuclear matter for conventional choice using the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared with F and P. From the figures (3.6) and (3.7) it is observed that when the density of symmetric nuclear matter increases the pressure of symmetric nuclear matter first decreases and after that increases.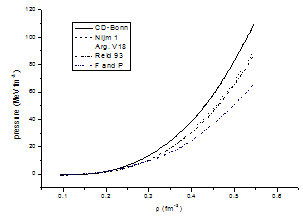 | Figure 3.7. The same as Fig. (3.6) but at T=10 MeV |
3.6. Nuclear Matter Incompressibility
The incompressibility κ0[27] can be calculated from the following equation: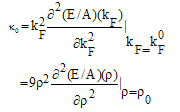 | (3.6) |
The incompressibility κ 0 can be used to explain the stiffness of the EOS. The experimental value of the incompressibility of nuclear matter at its saturation density ρ0 has been determined to be 210 ± 30 MeV[28].The incompressibility at the saturation point is computed in terms of saturation density ρ0 using different potentials. It is found that, for conventional choice the values of incompressibility for the CD-Bonn potential, the Nijm1 potential, the Reid93 potential and the Argonnev18 potential are: (228.97, 260.02, 235.95 and 233.42 MeV) respectively.
3.7. Symmetry Energy of the Asymmetric Nuclear Matter
The symmetry energy is defined as 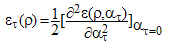 | (3.7) |
where ατ is the neutron excess parameter. In Fig. (3.8) for conventional choice, symmetry energies in MeV are plotted against the density ρ in (fm-3), in comparison with the experimental data using the CD-Bonn potential (solid line), the Nijm1potential (dashed line), the Reid 93 potential (dashed dot line) and the Argonne v18 potential (dot line), and the experimental data[29] are represented by dashed double dots line. From figure (3.8), it is observed that when the density of nuclear matter increases the symmetry energy of the system increases. For all the potentials at the saturation density (ρ0 = 0.16 fm-3) it is found that the nuclear symmetry energy is around 32 MeV.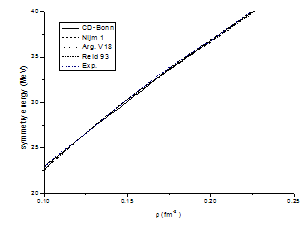 | Figure 3.8. The symmetry energy in (MeV) as a function of density ρ in (fm-3) is compared by exp. data [29] using different potentials for conventional choice |
4.1. EOS of the Pure Neutron Matter at (T = 0)
By using the values of t1, t2, x1 and x2 (interaction parameters) from table (2) the EOS of the pure neutron matter is calculated by adding the BHF calculation to the Skyrme one.Table 2. The interaction parameters for various potentials
 |
| |
|
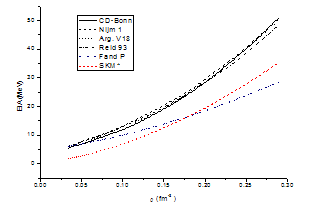 | Figure 4.1. E / A in MeV for pure neutron matter at (T = 0) as a function of density in (fm-3) using different potentials for conventional choice compared by SKM*[30], F and P [25] |
The results are shown in figure (4.1) where the energy per particle (E / A) in MeV is plotted against density ρ in fm-3, for pure neutron matter using different potentials. The results obtained are compared by SKM*[30], and F and P[25].From figure (4.1) it is observed that when the energy per nucleon increases the density increases, and all potentials behave in the same way as the SKM* potential.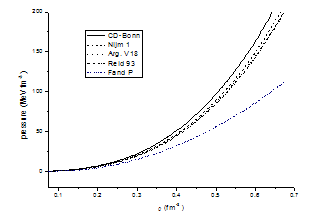 | Figure 4.2. Pressure of the pure neutron matter in (MeV.fm-3) at (T = 0) as a function of density ρ in (fm-3) using different potentials for conventional choice in comparison with F and P [25] |
4.2. Pressure of the Pure Neutron Matter at (T = 0)
Adding the quantity ∆P (ρ) (Skyrme) to the pressure calculated by the Brueckner-Hartre-Fock approximation, the results are shown in figure (4.2), the values of pressure are plotted against the density ρ, for pure neutron matter using different potentials in comparison with F and P[25]. From Fig. (4.2) it is observed that when the density of pure neutron matter increases the pressure increases.
4.3. Single Particle Potential of the Pure Neutron Matter
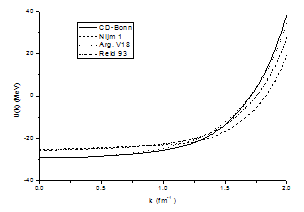 | Figure 4.3. The single particle potential for the pure neutron matter in (MeV) as a function of momentum k at (kF = 1.333 fm-1) for conventional choice of different potentials |
The single particle potential for the pure neutron matter is calculated using the CD-Bonn potential, the Argonnev18, the Nijm1 potential and the Reid 93 potential for conventional choice. In figure (4.3) the dependence of the single particle potential on the momentum k for the pure neutron matter at kF = 1.333 fm-1 is plotted for various potentials .It is observed that the results for all potentials are similar in the conventional choice. The single particle potential increases with increasing the momentum k.
4.4. Free Energy of the Pure Neutron Matter at Different T
The free energy of the pure neutron matter is defined by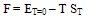 | (4.1) |
Where F is the free energy of the system, ET=0 is the total energy at T = 0 and ST is the entropy of the system at temperature T. Using T2-approximation[25], the entropy of pure neutron system at temperature T is defined by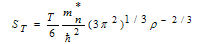 | (4.2) |
By substituting equation (4.2) in equation (4.1) then the free energy F is given by: 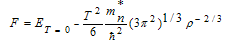 | (4.3) |
where 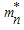 is the effective mass of the neutron
is the effective mass of the neutron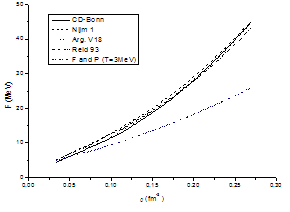 | Figure 4.4. The free energy at (T = 3 MeV) for pure neutron matter in [MeV] as a function of density in [fm-3] using different potentials for conventional choice compared by F and P[25] |
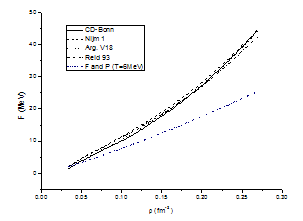 | Figure 4.5. The same as figure (4.4) but at T=6MeV |
The results are shown in figures (4.4) and (4.5), for the pure neutron matter using different potentials in comparison with F and P[25]. In Fig. (4.4) for conventional choice at T = 3 MeV, the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared with F and P. In Fig.(4.5) for conventional choice at T = 6 MeV, the CD-Bonn potential, the Nijm1 potential, the Argonne v18 potential and the Reid 93 potential are compared with F and P.From the figures (4.4) and (4.5), it is observed that when the density of pure neutron matter system increases the free energy of this system increases and all potentials have the same behaviour.
4.5. Pressure of the Pure Neutron Matter at Different T
At (T = 3 and 6 MeV) the following equation is used to calculate the pressure of the pure neutron matter by using T2-approximation [26]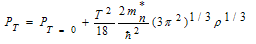 | (4.4) |
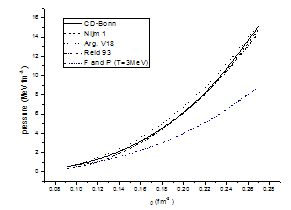 | Figure 4.6. Pressure of the pure neutron matter in (MeV.fm-3) at (T = 3 MeV) as a function of density in [fm-3] using different potentials for conventional choice |
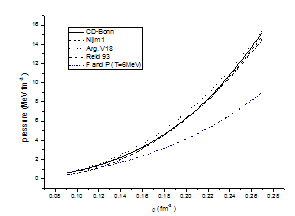 | Figure 4.7. The same as figure (4.6) but at T=6MeV |
The results are shown in Fig. (4.6). Values of the pressure at (T = 3 MeV) are plotted against the density ρ for pure neutron matter for conventional choice using the CD-Bonn potential, the Nijm1 potential, the Reid 93 potential and the Argonne v18 potential in comparison with F and P.In Fig. (4.7), values of the pressure at (T = 6 MeV) are plotted against the density ρ for pure neutron matter for conventional choice using the CD-Bonn potential, the Nijm1 potential, the Reid 93 potential and the Argonne v18 potential in comparison with F and P . From the figures (4.6) and (4.7) it is observed that when the density of pure neutron matter increases the pressure of pure neutron matter increases and all potentials have the same behaviour.SummaryThe bulk properties of symmetric nuclear matter and pure neutron matter are computed such as the equation of state (EOS), pressure, entropy, free energy, single particle potential, nuclear matter incompressibility and the symmetry energy as a function of the density. The calculation of the above properties for symmetric nuclear matter and pure neutron matter are made by using BHF interaction + two body density dependent Skyrme interaction which is equivalent to three body interaction. In this way we were able to obtain the correct experimental value of E/A for nuclear matter. Also we obtained the correct behaviour of the symmetry energy in comparison with the experimental work of Shetty et al.[29]. Modern NN interactions as the CD-Bonn potential, the Nijm1 potential, the Reid 93 potential and the Argonne v18 potential are used in order to analyse the dependence of the results on the nuclear interaction. The EOS and the pressure for both symmetric nuclear matter and pure neutron matter are calculated at (T = 0).The free energy and the pressure of symmetric nuclear matter at (T= 5 and 10 MeV) and of pure neutron matter at (T= 3 and 6 MeV) have been calculated by using T2-approximation[26]. The results are good in comparison with F and P[25]. One concludes that the calculations is only suitable at low densities and are comparable at higher densities. By this method good agreement is obtained in comparison with previous theoretical calculation using realistic potential of F and P and the experimental data. We conclude that the BHF theory in addition to our suggested contact interaction are able to produce the experimental saturation point for the equation of state and overall good agreement with the realistic force calculation of F and P for T=0 (among the different choices of the sets of parameters t i and x i best results were obtained for the set of parameters given here using the values 1/3 and 2/3 for α). The parameters were obtained by fitting the values of E/A and the pressure at the saturation density besides two points from the symmetry graph. Comparable results are obtained for finite temperatures. Good agreement is obtained for the symmetry energy with a noticeable increase with the density in comparison with the experimental data. Two terms are used only in our suggested potential but one can add more terms to calculate other physical quantities (the neutron matter data were not taken in the fitting procedure in the present work). In this case the treatment will be more involving. One final comment is that similar results were obtained using the continuous choice in comparison with the conventional choice presented here.
References
| [1] | A. Peshier, B. Kämfer and G. Soft, phys. Rev. C 61 (2000) 045203. |
| [2] | K. C. Chung, C. S. Wang, A. J. Santiago and J. W. Zhang Phys. Rev. C 61 (2000) 047303. |
| [3] | J. Margueron, E. van Dalen, C. Fuchs, Phys. Rev.C 76 (2007) 034309. |
| [4] | G.F. Bertsch and S. Das Gupta, Phys. Rep. 160 (1988) 189; P. Danielowicz, Critical Phenomena and Collective Observable, 327, S. Costa, S. Albergo, A. Insolia and C. Tuve Eds., World Scientific 1996; D.H.E. Gross et al, Phys. Rep. 279 (1971) 19. |
| [5] | A.L. Fetter and J.D. Walecka, Quantum Theory of Many Particle Physics (McGraw-Hill, New York, 1971). |
| [6] | J. W. Negele and H. Orland, Quantum Many-Particle Systems (Addison- Wesley, Redwood City, 1988). |
| [7] | J. Goldstone, Proc. Roy. Soc. () A239 (1957) 267; H. A. Bethe and J. Goldstone, Proc. Roy. Soc. () A238 (1957) 551. |
| [8] | See for instance B.D. Day, Rev. Mod. Phys. 39 (1967) 719; C. Mahaux, in the Many-Body Problem, Jastrow Correlations versus Brueckner Theory, Lecture Notes in Physics 138, R. Guardiola and J. Ros Eds., Springer-Verlag (1980). |
| [9] | D.W.L. Sprung, Nuclear Matter calculations, Adv. Nucl. Phys., Vol. 5, J.W. Negele and Eds., Plenum Press (1975). |
| [10] | F. Coestor, S. Cohen, B.D. Day, and C.M. Vincent, Phys.Rev. C1 (1970) 769. |
| [11] | R.B. Wiringa, V. Fiks, and A. Fabrocini, Phys. Rev. C38 (1988) 1010. |
| [12] | A. Akmal and V.R. Pandharipande, Phys. Rev. C56 (1997) 2261; A. Akmal and V.R. Pandharipande, Phys.Rev. C58 (1998) 1804. |
| [13] | M. Baldo, Bombaci, and G.F. Burgio, Astron. Astrophys.328 (1997) 274. |
| [14] | P. Gögelein, E. N. E. van Dalen, Kh. Gad, Khaled S. A. Hassaneen, and H. Müther, Phys. Rev. C 79, 024308 (2009). |
| [15] | M. Baldo and Alaa Eldeen Shaban, Phys. Lett. B661, 373 (2008). |
| [16] | Z. H. Li, U. Lombardo, H.-J. Schulze, W. Zuo, L. W. Chen, and H. R. Ma, Phys. Rev. C 74, 047304 (2006). |
| [17] | Machleidt R. Phys. Rev. C 63 (2001) 024001. |
| [18] | Wiringa R. B, Stoks V. G. J. and Schiavilla R, Phys. Rev. C 51 (1995) 38. |
| [19] | Stoks V. G. J, Klomp R. A. M, Terheggen C. P. F and de Swart J. J, Phys. Rev. C 49 (1994) 2950. |
| [20] | Kümmel H, Lührmann K. H. and Zabolitzky J. G. Phys. Rep. 36 (1978) 1. |
| [21] | Prakash M. Phys. Rep. 242 (1994) 191. |
| [22] | Khaled S. A. Hassaneen, H. M. Abo-Elsebaa, E. A. Sultan, and H.M.M. Mansour,Annals of Physics 326 (2011) 566. |
| [23] | J.P. Jeukenne, A. Leijeune and C. Mahaux, Phys. Reports 25, (1976) 83. |
| [24] | C. Mahaux, R. Sartor, Adv. Nucl. Phys.20 (1991) 1 |
| [25] | B. Freidman and V. R. Pandharipande. Nucl. Phys. A 361 (1981) 502. |
| [26] | H. M. M. Mansour, M. Hammad and M. Y. M. Hassan. Phys. Rev. C 56 (3) (1997) 1418. |
| [27] | J. P. Blaizot, J. F. Berger, J. Dechargé and M. Girod. Nucl. Phys. A 591 (1995) 435. |
| [28] | J. P. Blaizot, Phys. Report. 64, (1980) 177. |
| [29] | S. J. Yennello, D. V. Shetty and G. A. Souliotis, arXive: nucl-ex / (2006) 0601006. |
| [30] | E. Chabanat, P. Bonche, P. Haensel. J. Meyer and R. Schaeffer.Nucl. Phys. A 627 (1997) 722. |

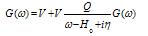
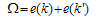
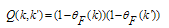
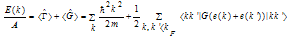
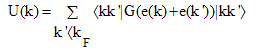
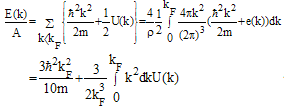
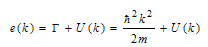
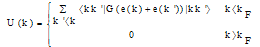
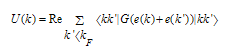
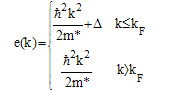
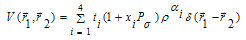

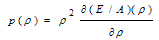


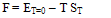
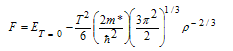


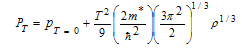


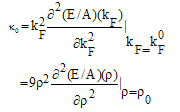
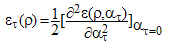




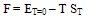
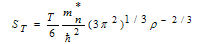
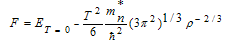
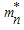 is the effective mass of the neutron
is the effective mass of the neutron

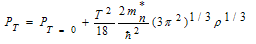


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
