1. Introduction

Transitions between different phases of nuclear matter produced in relativistic nucleus-nucleus collisions is one of the main subjects in experimental high energy physics. To see the phase evolution, one analyses various characteristics of particle production at nuclear-nuclear collisions depending on the centrality of collisions[1–6]. However, there is problem to define the centrality experimentally. Therefore, in different experiments[1-6] the centrality is defined as a number of identified protons, projectile and target fragments, slow particles, all particles, as the energy flow of the particles with emission angles equal 0◦ or 90◦, etc. Glauber modelling[7] which contains some theoretical approximations enables one to establish approximately the centrality with the aid of the impact parameter b and the multiplicity of identified secondary charged particles in experiments. But, however, there is a model dependent definition of the centrality and, the absence of unique criterion for the centrality.

2. Method

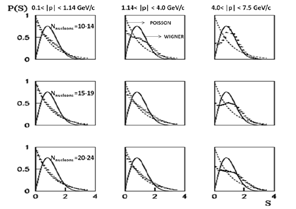
In paper[8] one has suggested that tools from Random Matrix Theory (RMT)[9, 10] might be useful in illuminating the presence of correlations in the spectral (momentum) distribution of secondary particles produced in nucleus-nucleus collisions at high energy. Indeed, one have found a good agreement between the results obtained in this way and a standard analysis based on the method of effective mass spectra and two-pair correlation function often used in high energy physics[11]. It have been demonstrated that the RMT approach does not depend on the background of measurements and relies only on fundamental symmetries preserved in nucleus-nucleus collisions. The purpose of the present paper is to suggest novel criteria for the centrality of collision, using a new method which is based on Random Matrix Theory (RMT)[8-11] that was originally introduced to explain the statistical fluctuations of neutron resonances in compound nuclei[12]. The theory assumes that the Hamiltonian belongs to an ensemble of random matrices that are consistent with the fundamental symmetries of the system. Besides these general symmetry considerations; there is no need in other properties of the system under consideration. It is assumed that the momentum distribution of secondary particles produced in nucleus-nucleus collisions may be associated with Eigen states (quantum levels) of a composite system. It is, therefore, natural to use the momentum as a proper variable for the analysis in order to avoid possible errors at the transformation from the momentum to the energy, which requires an accurate determination of the corresponding mass value.

In general, this procedure does not involve any uncertainty or spurious contributions and deals with a direct processing of physical data. If the “events” {x_i} are independent, i.e., correlations in the system under consideration are absent, the form of the histogram must follow p(s) = exp (-s) known as the Poisson density. The Poisson spectrum corresponds to the dominance of many crossings between different energies (momenta). On the other hand, if the levels are repelled, the density is approximately given by the Wigner surmise form p(s) = (π/₂) s exp (-π/₄s²). In turn, the crossings are usually observed when there is no mixing between states that are characterized by different good quantum numbers, while the anti crossings signal about a strong mixing due to a perturbation brought about by either external or internal sources. In other words, any correlations that produce the deviation from the regular pattern (Poisson distribution): production of a collective state (resonance), or some structural changes in the system under consideration would be uniquely identified from the change of the histogram shape.

To clearly recognize correlations the total set of spacing’s {s_i} has been divided on three sets, in correspondence with three regions of the measured momenta: a) 0.1 < |p| < 1.14 GeV/c (region I); b) 1.14 < |p| < 4.0 GeV/c (region II) ;c) 4.0 < |p| < 7.5 GeV/c (region III) (see Fig.1&2). The region boundaries were determined with the requirement that the shape of the spacing density P(S) does not change in the region under consideration. For example, the decrease of the upper bound of the region I does not change the Poisson distribution. However, the increase of this boundary leads to the deviation from the latter distribution. The same criteria have been applied for the second and third regions. Note that there is no a prescribed procedure how to define such regions. However, the empirical approach described above proved to be useful in data processing for various systems at the RMT analysis[9, 12]. In the present paper the nearest-neighbor momentum spacing distribution P(S), related to secondary nucleons (p, n) and neutral particles (n, ⁰) particles are considered.

3. Dubna Cascade Model

To shed light on the production of the secondary particles, a fully integrated Monte Carlo simulation package[13] of Dubna Cascade Model (DCM)[14-19] has been used. The Dubna Cascade model is aimed for simulation of nucleus-nucleus collisions at relativistic energies. Simulating the secondary particles production in ¹²C+¹²C collisions at a momentum of 4.2A GeV/c with the aid of Dubna Cascade Model.

4. Results and Discussions

One can obseve that the Poisson type behavior in first region and likes Wigner in third region but a mixed type behavior in second region as shown in Fig.1&2.It means that there is no correlation in first region and strong correlation in the third region as shown in Fig.1&2.The results shown in Fig.1&2 are for all nucleons (p, n) and all neutral particles (n, ⁰) produced in simulation from Dubna Cascade model.

To see the behavior of the nearest neighbor spacing momentum distributions P(S) with multiplicity, the events for nucleons has been separated in three groups: i) the events with N_nucleons = 10 − 14 secondary nucleons; ii) the events with N_nucleons = 15 − 19 nucleons; ii) the events with N_nucleons = 20 − 24 nucleons as shown in Fig.3. Similarly the events for neutral particles have been separated in three groups: i) the events with N_neutral = 10 − 14 secondary neutral particles; ii) the events with N_neutral = 15 − 19 secondary neutral particles; ii) the events with N_neutral = 20 − 24 secondary neutral particles as shown in Fig.4.In these cases, the separation was also done according to the criteria discussed above. However, as a starting point the experimental behavior of the various nearest neighbor spacing momentum distributions P(S) as a function of multiplicity has been used.

One evidently recognizes the onset of correlations for N_nucleons = 10 – 14 and N_neutral = 10 – 14 with the increase of the absolute value of the momentum distribution (see Fig.3&4, top row, from left to right). The onset of correlations in the interval 1.14 < |p| < 4.0 GeV/c (the region II), found in virtue of the RMT analysis, owes their origin to the protons produced as a result of decays of well known Δ⁺⁺-isobars with masses m_Δ++ = 1.232 and1.650 (GeV/c²)[11]. The presence of the sharp peak in the third interval 4.0 < |p| < 7.5 GeV/c (the region III) can be attributed to the interaction between stripping protons in the final state, which dominate in the peripheral collisions. Indeed, one could found that strong correlations are brought about by the protons pairs with zero angle in the momentum distribution interval 4.0 < |p| < 7.5 GeV/c. This interpretation becomes even more convincing with the increase of all secondary particles number (N_nucleons = 15−19 and N_neutral = 15−19; see Fig.3&4, right column). With the increase of the multiplicity of nucleons and neutral secondary particles, the number of the stripping protons decreases as shown in Fig.3&4. As a result, the correlations, brought about by these proton pairs, decreases as well. For the multiplicity N_nucleons = 20−24 and N_neutral = 20−24 the distribution is neither the Poisson nor the Wigner surmise. Note, however, that the number of participants is increased, which can be associated with the onset of the central collisions.

The model results show the existing of some peaks in the region II and their transformation to the Wigner distribution in the region III. Evidently, the model results demonstrate the existing of some non-trivial non-kinematic correlations for the nucleons and neutral particles in the regions II and III. This analysis provides the basis to identify the critical multiplicity that would signal on the onset of central collisions. Indeed, the Dubna Cascade model enables us to solve several problems of practical importance.

Figure 1. The P(S) distributions based on the DCM results, for different regions of the momentum: the first column corresponds to 0.1 < |p| < 1.14 GeV/c; the second column corresponds to 1.14 < |p| < 4.0 GeV/c; the third column corresponds to 4.0 < |p| < 7.5 GeV/c. The P(S) distribution for all nucleons . The Poisson and the Wigner surmise distributions are connected by dashed and solid lines, respectively

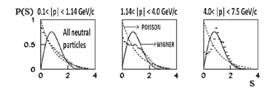Figure 2. Same as Fig.1 but for neutral particles

Figure 3. The P(S) distributions based on the DCM results, for different regions of the momentum: the first column corresponds to 0.1 < |p| < 1.14 GeV/c; the second column corresponds to 1.14 < |p| < 4.0 GeV/c. The P(S) distribution for different values of the nucleons: the top row corresponds to Nnucleon=10–14; the middle row corresponds to Nnucleon =15–19 and the bottom row corresponds to Nnucleon =20–24. The Poisson and the Wigner surmise distributions are connected by dashed and solid lines, respectively

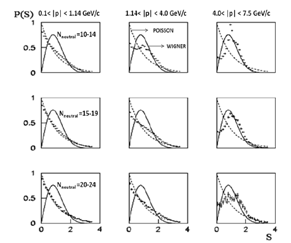Figure 4. Same as Fig.3 but for neutral particles

5. Conclusions

In conclusion, one has proposed a novel criterion to define the centrality of the nucleus-nucleus collisions, using the procedure developed in the framework of the RMT approach. The transition from the Poisson distribution to the Wigner surmise distribution signals on the onset of correlations. In turn, the centrality of nucleus-nucleus collisions is associated with the absence of correlations.