Ahmad Salar Elahi , Mahmood Ghoranneviss
Plasma Physics Research Center, Science and Research Branch, Islamic Azad University, Tehran, Iran
Correspondence to: Ahmad Salar Elahi , Plasma Physics Research Center, Science and Research Branch, Islamic Azad University, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Main purposes of this contribution are analysis of dynamic equilibrium properties of a large aspect ratio and low beta tokamaks, in particular deriving a modified relation for the Shafranov shift in the presence of poloidal flow, and demonstrate it experimentally. Poloidal flow can produce modifications in the equilibrium properties. By increasing Alfvenic Mach number from zero, flow produce outward force, and plasma shifted in outward direction. If the poloidal Alfvenic Mach number equal to one, singularity will observe in the solution of generalized Grad-Shafranov equation. Also inversion of Shafranov shift in the transition of flow speed between sub-Alfvenic to super-Alfvenic speeds can be observed due to inward force produced by flow.
Keywords:
Tokamak, Equilibrium, Poloidal Flow, Shafranov Shift
1. Introduction
There has been an increasing attractive in the investigations of the equilibrium properties of tokamak plasmas with poloidal and toroidal flow. A precision investigation of the magnetic equilibrium is essential to interpret information from most other diagnostics and for further investigations such as Magnetohydrodynamics equilibrium and stability analysis, plasma confinement and transport studies. Also determination of the plasma equilibrium position during confinement time is essential to transport it to the control system based on feedback. However, in solving of the equilibrium problem, usually simplifying approximations have been used, e.g. axisymmetric in toroidal direction or assumption of static plasma (zero toroidal or poloidal flow), but in some cases may be these approximations not correct perfectly, for example in cases of auxiliary heating e.g. neutron beam injection, error percent can be increased with neglecting the toroidal flow. But in tokamaks which have not auxiliary heating such as the IR-T1 tokamak (see Table 1), neglecting the toroidal flow is good approximation. Instead, we suppose that poloidal flow is present in our discussion. Although this problem already had discussed for high beta tokamaks in the few works, we modified it for low beta regimes in order to use in IR-T1[1-14]. In section 2 we will be showed analytically that in presence of poloidal flows for the large aspect ratio and low beta tokamaks, changes in equilibrium properties can be observed. In the section 3 we will be derived the Shafranov shift by regarding of poloidal flow. We also will be presented experimentally in section 4, brief review for determination of the plasma position with and without regarding of the poloidal flow and also plasma rotation. Summary and conclusion are will be presented in section 5.
2. Tokamak Plasma Equilibrium with Poloidal Flow
An analytic model can be derived for flowing low beta plasmas, using an expansion in terms of inverse aspect ratio ε . The plasma is described using the ideal isotropic magnetohydrodynamics model. The main concepts of this expansion used in here derived in[1], which will be modified to include the effect of poloidal flow in low beta tokamaks. The basic assumptions are large aspect ratio 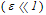 , low β
, low β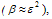 circular cross section, and Alfvenic poloidal flow with constant poloidal Alfvenic Mach number. For these assumptions, in addition to the usual assumption of axisymmetry we allow to write the Grad-Shafranov equation in the following generalized form[2]:
circular cross section, and Alfvenic poloidal flow with constant poloidal Alfvenic Mach number. For these assumptions, in addition to the usual assumption of axisymmetry we allow to write the Grad-Shafranov equation in the following generalized form[2]: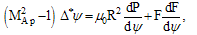 | (1) |
where 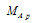 is the poloidal Alfvenic Mach number which defined below. The set of reduced equations for ideal MHD equilibria in deriving Eq. (1), the plasma flow and
is the poloidal Alfvenic Mach number which defined below. The set of reduced equations for ideal MHD equilibria in deriving Eq. (1), the plasma flow and  defined by:
defined by: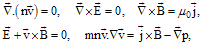 | (2) |
 Where we used the cylindrical coordinates
Where we used the cylindrical coordinates  , and
, and  are two free functions of
are two free functions of  describing the parallel and toroidal components of the velocity respectively. For simplicity assume that the calculation has been carried out in the toroidal coordinates
describing the parallel and toroidal components of the velocity respectively. For simplicity assume that the calculation has been carried out in the toroidal coordinates 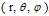 , and we have:
, and we have: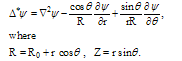 | (3) |
In the ohmically heated tokamaks (low beta regime) the assumptions in order 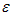 is given by:
is given by: 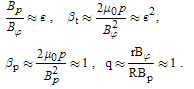 | (4) |
We can solve the generalized Grad-Shafranov equation for ohmically heated tokamaks by expanding as follows: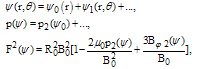 | (5) |
where the subscripts 1, and 2 indicate the ordering in ,
, 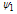 is the first order solution of the general GSE equation, R0 is the major radius of the plasma,
is the first order solution of the general GSE equation, R0 is the major radius of the plasma,  is the vacuum toroidal field atR=R0, and
is the vacuum toroidal field atR=R0, and 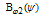 is a new free function replacing
is a new free function replacing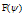 . As shown in Eq. (5), the expressions for
. As shown in Eq. (5), the expressions for  and
and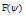 are in order S2 (accurate for low beta regime tokamaks), as:
are in order S2 (accurate for low beta regime tokamaks), as: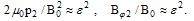 | (6) |
Substituting the Eq. (3) and Eq. (5) in the Eq. (1), we can write: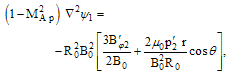 | (7) |
where prime denotes differentiation with respect to 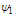 Since Eq. (7) is a nonlinear two-dimensional partial differential equation, in approximation of radial pressure balance and toroidal force balance, for special choices of
Since Eq. (7) is a nonlinear two-dimensional partial differential equation, in approximation of radial pressure balance and toroidal force balance, for special choices of 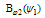 and
and , it can be solved analytically. A simple model is discussed below which first investigated in[3].Consider the case where
, it can be solved analytically. A simple model is discussed below which first investigated in[3].Consider the case where 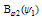 and
and  are linear in
are linear in  so that:
so that: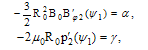 | (8) |
and assume the plasma surface is circular with radius a. The appropriate boundary condition is a constant value for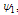 , which is convenient to set to zero (equal to zero pressure). The linear dependence of
, which is convenient to set to zero (equal to zero pressure). The linear dependence of 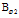 implies that the toroidal current density is nearly uniform. Therefore Eq. (7) reduces to:
implies that the toroidal current density is nearly uniform. Therefore Eq. (7) reduces to: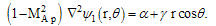 | (9) |
The solution for  are easily found:
are easily found: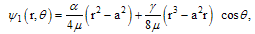 | (10) |
where 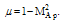 We express the constants
We express the constants 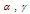 in terms of the physical parameters,
in terms of the physical parameters, 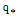 and
and , the results are:
, the results are: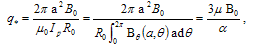
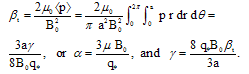 | (11) |
Substituting these values in Eq. (10) leads to the following equilibrium solution of Eq. (9) for a plasma with poloidal flow, for the low beta tokamaks: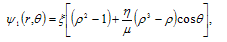 | (12) |
where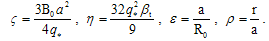 | (13) |
Where Ip is the plasma current,βt the toroidal Beta, 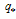 represents an integrated safety factor, η is basically measure the plasma Beta, µ is measure the flow, and ρ is implying a normalized minor radius.If there are external coils to produce vertical magnetic field, the boundary condition on the flux function is modified so that we have[1]:
represents an integrated safety factor, η is basically measure the plasma Beta, µ is measure the flow, and ρ is implying a normalized minor radius.If there are external coils to produce vertical magnetic field, the boundary condition on the flux function is modified so that we have[1]: 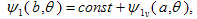 | (14) |
where 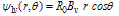 is the flux function due to external vertical field coils.Therefore the full correction to
is the flux function due to external vertical field coils.Therefore the full correction to 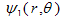 be:
be: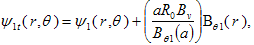 | (15) |
where 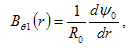 (16)and
(16)and  is the average vertical magnetic field over the vacuum chamber. It must be noted that the solution in equation (15) is valid for both
is the average vertical magnetic field over the vacuum chamber. It must be noted that the solution in equation (15) is valid for both  The condition
The condition 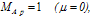 represents however a singular point of Eq. (9), where Eq. (12) do not hold. The solution in Eq. (15), contain all the informations required to describe the equilibrium, in particular the poloidal component of the magnetic field and the Shafranov shift.
represents however a singular point of Eq. (9), where Eq. (12) do not hold. The solution in Eq. (15), contain all the informations required to describe the equilibrium, in particular the poloidal component of the magnetic field and the Shafranov shift.
3. The Shafranov shift in Presence of the Poloidal Flow
In this section we will present the analytical representation for the shift of the magnetic axis from the geometrical axis (the Shafranov shift). The Shafranov shift is determined by the position of the maximum of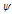 , or in other words zero value for poloidal field inside the plasma. This can be found by solving the equation
, or in other words zero value for poloidal field inside the plasma. This can be found by solving the equation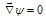 . The Ф derivative can only vanish on the midplane, and this leaves again a single equation for the radial component of the gradient, which is proportional to the poloidal component of the magnetic field. The Shafranov shift can therefore be determined by solving:
. The Ф derivative can only vanish on the midplane, and this leaves again a single equation for the radial component of the gradient, which is proportional to the poloidal component of the magnetic field. The Shafranov shift can therefore be determined by solving: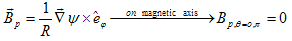 | (17) |
The value of the Shafranov shift in present of the poloidal flow and external vertical field indicating with ΔR, and Eq. (17) can be solved to give: 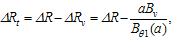 | (18) |
Where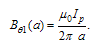 | (19) |
Therefore we can write: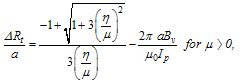 | (20) |
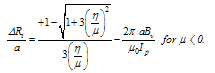 | (21) |
Therefore for flow speed lower and upper than Alfvenic speed in absence of external vertical field there is inversion of Shafranov shift.
4. Experimental Determination of the Plasma Rotation and Equilibrium Position
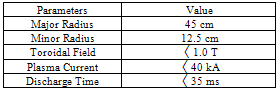
IR-T1 is a low beta, large aspect ratio, and circular cross-section tokamak (see Table (1)), which has two stainless steel grounded fully poloidal limiters with radiuses of 12.5cm. The main diagnostics used in this work are a diamagnetic loop and a poloidally and toroidally oriented Mach probes. The experiments were performed in hydrogen. An average plasma density was in the range 0.7-1.5X1013 cm-3, the toroidal magnetic field induction , the plasma current
, the plasma current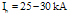 . Measurements of the plasma parameters were performed using single Langmuir probe, diamagnetic loop and a poloidally and toroidally oriented Mach probes. Theoretical models have been derived to describe the Mach probes data in un-magnetized and magnetized plasmas, using fluid, particle, and kinetic models (see the Figure (1)) [15-20]. Figure (2) shows the time dependence of the ion saturation currents collected by the poloidal Mach probes, the ratio of upstream to downstream current, and the resulting Mach number. The Mach number and thus the poloidal plasma velocity are obtained using the model of Hutchinson.
. Measurements of the plasma parameters were performed using single Langmuir probe, diamagnetic loop and a poloidally and toroidally oriented Mach probes. Theoretical models have been derived to describe the Mach probes data in un-magnetized and magnetized plasmas, using fluid, particle, and kinetic models (see the Figure (1)) [15-20]. Figure (2) shows the time dependence of the ion saturation currents collected by the poloidal Mach probes, the ratio of upstream to downstream current, and the resulting Mach number. The Mach number and thus the poloidal plasma velocity are obtained using the model of Hutchinson. 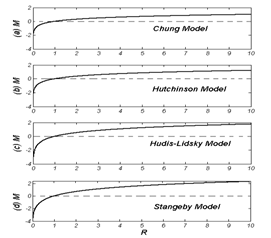 | Figure 1. Theoretical models which described the ratio of ion saturation current (R) dependence of the Mach number (M), (a) the Chung model, (b) Hutchinson model, (c) Hudis-Lidsky model, and (d) the Stangeby model. |
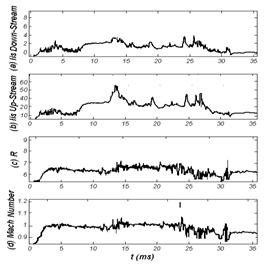 | Figure 2. (a) Down-stream ion saturation current, (b) Up-stream ion saturation current, (c) Ratio of ion saturation currents, and (d) Poloidal Mach number. |
For measurement of the plasma column displacement we need to obtain a toroidal beta, plasma current, vacuum toroidal field, and, moreover a vertical field. Plasma current can be measured by a Rogowski coil, vacuum toroidal field can be measured by a diamagnetic loop, and also vertical field can be measured by a saddle coil or a magnetic probe. But for determination of the toroidal Beta, from approximation for the ohmically heated tokamaks, we have: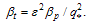 | (22) |
There are two methods for determination of the poloidal Beta: diamagnetic loop method, and magnetic probe method. We used the first method. The diamagnetic loop consists of a simple loop that links the plasma column, ideally located in a poloidal direction in order to minimize detecting the poloidal field. In cases of the ohmically heated tokamaks (low beta) where the plasma energy density is small compared to the energy density of the magnetic field, the change in the total toroidal magnetic flux is small. Therefore a reference signal equal to the vacuum toroidal magnetic flux is usually subtracted from it, giving a net toroidal flux equal to the diamagnetic flux  produced by the circular plasma. Relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation [4]:
produced by the circular plasma. Relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation [4]: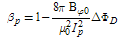 | (23) |
where 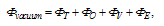
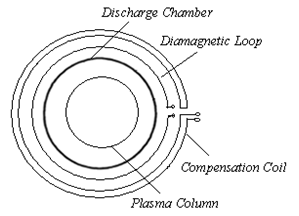 | Figure 3. Positions of the diamagnetic loop with its compensation coil on outer surface of the IR-T1 Tokamak Chamber |
and where 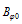 is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe,
is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe, 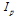 is the plasma current which can be obtained by the rogowski coil,
is the plasma current which can be obtained by the rogowski coil,  is the toroidal flux because of toroidal field coils,
is the toroidal flux because of toroidal field coils, 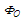 and
and 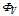 are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and
are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and 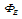 is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or fields discharge without plasma. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received (see Figure (3)). As shown in Eq. (23) the diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux
is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or fields discharge without plasma. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received (see Figure (3)). As shown in Eq. (23) the diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux 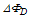 caused by plasma current can be measured from the diamagnetic and compensating coil using subtraction.
caused by plasma current can be measured from the diamagnetic and compensating coil using subtraction. Table 1. Main Parameters of the IR-T1 Tokamak
 |
| |
|
By substituting the toroidal beta obtained from diamagnetic loop, plasma current measured using the Rogowski coil, vacuum toroidal field obtained from diamagnetic loop, the average vertical field obtained from Saddle coil, and different values of Alfvenic Mach number in Eqs. (15), (18), and (19), magnetic flux surfaces and displacement of plasma column center obtained as shown in Figures (4), (5), (6), and (7).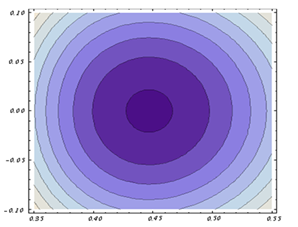 | Figure 4. Magnetic Flux Surfaces for t=15ms in target shot in IR-T1 tokamak, in case of Alfvenic Mach number () equal to zero. |
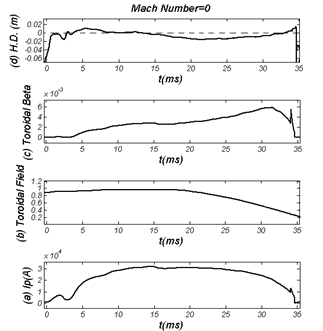 | Figure 5. (a) Plasma Current, (b) Toroidal Magnetic Field, (c) Toroidal Beta, and (d) Horizontal Displacement (H.D.) in case of that Poloidal Alfvenic Mach number () equal to zero in IR-T1 tokamak |
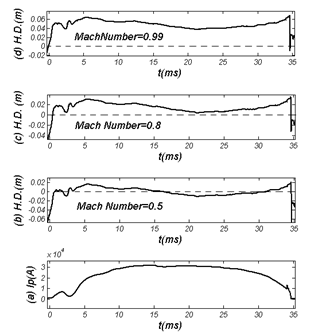 | Figure 6. Effects of Alfvenic Mach number () on Horizontal Displacement (H.D) in IR-T1 Tokamak, (a) Plasma Current, (b) H.D in case of that =0.5 (c) H.D in case of =0.8, and (d) H.D in case of =0.99. Increasing the values of the , flow produce outward force (plasma column displacement is increased in outward direction) |
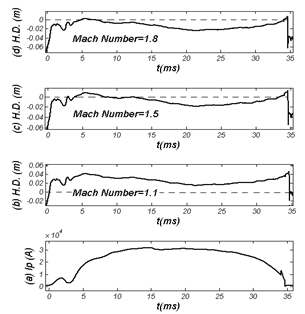 | Figure 7. Effects of Alfvenic Mach Number (AMn) on Horizontal Displacement (H.D) in IR-T1 Tokamak, (a) Plasma Current, (b) H.D in case of that =1.1 (c) H.D in case of =1.5, and (d) H.D in case of =1.8. Increasing the values of from 1, flow produce inward force (plasma column displacement is inverted). |
5. Summary and Conclusions
In this paper we presented analysis of dynamic equilibrium properties of tokamaks, in particular deriving a modified relation for the Shafranov shift in the presence of Alfvenic poloidal flow and external vertical field, for large aspect ratio and low beta tokamaks. Results demonstrated experimentally on the IR-T1, which is the large aspect ratio and ohmically heated tokamak. In the presence of Alfvenic poloidal flows, singularity in equilibrium observed. By increasing the value of Alfvenic Mach number from zero, flow produces outward force. In the transition of flow speed between lower to upper than the Alfven speed, the Shafranov shift can be inverted due to inward force produced by flow.
References
| [1] | J. P. Freidberg, Ideal MHD (Clarendon, Oxford, 1987) |
| [2] | L. Guazzotto and R. Betti, Phys. Plasmas 12, 056107 (2005) |
| [3] | J. P. Freidberg and F. A. Haas, Phys. Fluids 16, 1909 (1973) |
| [4] | I. H. Hutchinson, Principles of Plasma Diagnostics, (Cambridge University Press, Cambridge, 1987) |
| [5] | L. Zakharov, Am. Bulletin, Phys. Society, Division of Plasma Physics, 45, 225 (2000) |
| [6] | W. Zhang, Z. Wu and D. Li, Phys. Plasmas 12, 042106 (2005) |
| [7] | H. Tasso and G. N. Throumoulopoulos, Phys. Plasmas 5, 2378 (1998) |
| [8] | J. P. Graves, R. J. Hastie and K. I. Hopcraft, Plasma Phys. Control. Fusion 42, 1049 (2000) |
| [9] | J. E. Rice, W. D. Lee, E. S. Marmar et al., Phys. Plasmas 11, 2427 (2004) |
| [10] | E. J. Strait and et al., Fusion Science and Technology, 53, pp. 304-330, (2008) |
| [11] | A. Salar Elahi and et al., 2009, J Fusion Energy 28 (4), DOI 10.1007/s10894-009-9198-x. |
| [12] | A. Salar Elahi and et al., Phys. Scripta 80, 045501 (2009), DOI |
| [13] | A. Salar Elahi and et al., Phys. Scripta 80, 055502 (2009), DOI |
| [14] | A. Salar Elahi and et al., IEEE T on Plasma Sci. 38 (2), DOI 10.1109/TPS.2009.2037965 |
| [15] | I. H. Hutchinson, Phys. Fluids 30, 3777 (1987). |
| [16] | I. H. Hutchinson, Phys. Rev. A 37, 4358 (1988). |
| [17] | B. J. Peterson et al., Rev. Sci. Instrum. 65 (8), 1994, 2599 |
| [18] | P. C Stangeby, Phys. Fluids 27, 2699 (1984) |
| [19] | K. S. Chung et al., Phys. Rev. A 38, 4721 (1988) |
| [20] | K. S. Chung et al., Phys. Fluids B 1, 2229 (1989) |

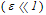 , low β
, low β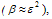 circular cross section, and Alfvenic poloidal flow with constant poloidal Alfvenic Mach number. For these assumptions, in addition to the usual assumption of axisymmetry we allow to write the Grad-Shafranov equation in the following generalized form[2]:
circular cross section, and Alfvenic poloidal flow with constant poloidal Alfvenic Mach number. For these assumptions, in addition to the usual assumption of axisymmetry we allow to write the Grad-Shafranov equation in the following generalized form[2]:
 is the poloidal Alfvenic Mach number which defined below. The set of reduced equations for ideal MHD equilibria in deriving Eq. (1), the plasma flow and
is the poloidal Alfvenic Mach number which defined below. The set of reduced equations for ideal MHD equilibria in deriving Eq. (1), the plasma flow and  defined by:
defined by:
 Where we used the cylindrical coordinates
Where we used the cylindrical coordinates  , and
, and  are two free functions of
are two free functions of  describing the parallel and toroidal components of the velocity respectively. For simplicity assume that the calculation has been carried out in the toroidal coordinates
describing the parallel and toroidal components of the velocity respectively. For simplicity assume that the calculation has been carried out in the toroidal coordinates  , and we have:
, and we have: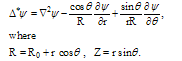
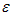 is given by:
is given by: 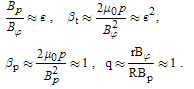
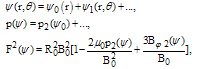
 ,
, 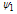 is the first order solution of the general GSE equation, R0 is the major radius of the plasma,
is the first order solution of the general GSE equation, R0 is the major radius of the plasma, 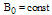 is the vacuum toroidal field atR=R0, and
is the vacuum toroidal field atR=R0, and 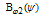 is a new free function replacing
is a new free function replacing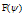 . As shown in Eq. (5), the expressions for
. As shown in Eq. (5), the expressions for  and
and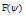 are in order S2 (accurate for low beta regime tokamaks), as:
are in order S2 (accurate for low beta regime tokamaks), as: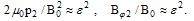
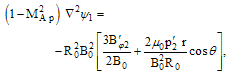
 Since Eq. (7) is a nonlinear two-dimensional partial differential equation, in approximation of radial pressure balance and toroidal force balance, for special choices of
Since Eq. (7) is a nonlinear two-dimensional partial differential equation, in approximation of radial pressure balance and toroidal force balance, for special choices of 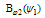 and
and , it can be solved analytically. A simple model is discussed below which first investigated in[3].Consider the case where
, it can be solved analytically. A simple model is discussed below which first investigated in[3].Consider the case where 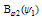 and
and  are linear in
are linear in  so that:
so that: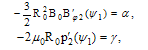
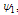 , which is convenient to set to zero (equal to zero pressure). The linear dependence of
, which is convenient to set to zero (equal to zero pressure). The linear dependence of 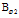 implies that the toroidal current density is nearly uniform. Therefore Eq. (7) reduces to:
implies that the toroidal current density is nearly uniform. Therefore Eq. (7) reduces to: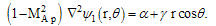
 are easily found:
are easily found: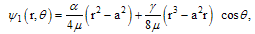
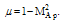 We express the constants
We express the constants 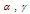 in terms of the physical parameters,
in terms of the physical parameters, 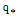 and
and , the results are:
, the results are: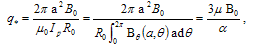
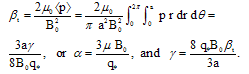
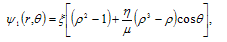
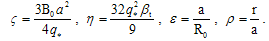
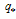 represents an integrated safety factor, η is basically measure the plasma Beta, µ is measure the flow, and ρ is implying a normalized minor radius.If there are external coils to produce vertical magnetic field, the boundary condition on the flux function is modified so that we have[1]:
represents an integrated safety factor, η is basically measure the plasma Beta, µ is measure the flow, and ρ is implying a normalized minor radius.If there are external coils to produce vertical magnetic field, the boundary condition on the flux function is modified so that we have[1]: 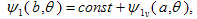
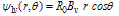 is the flux function due to external vertical field coils.Therefore the full correction to
is the flux function due to external vertical field coils.Therefore the full correction to 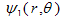 be:
be: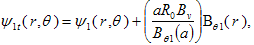
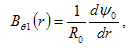 (16)and
(16)and 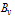 is the average vertical magnetic field over the vacuum chamber. It must be noted that the solution in equation (15) is valid for both
is the average vertical magnetic field over the vacuum chamber. It must be noted that the solution in equation (15) is valid for both 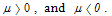 The condition
The condition 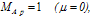 represents however a singular point of Eq. (9), where Eq. (12) do not hold. The solution in Eq. (15), contain all the informations required to describe the equilibrium, in particular the poloidal component of the magnetic field and the Shafranov shift.
represents however a singular point of Eq. (9), where Eq. (12) do not hold. The solution in Eq. (15), contain all the informations required to describe the equilibrium, in particular the poloidal component of the magnetic field and the Shafranov shift.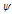 , or in other words zero value for poloidal field inside the plasma. This can be found by solving the equation
, or in other words zero value for poloidal field inside the plasma. This can be found by solving the equation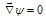 . The Ф derivative can only vanish on the midplane, and this leaves again a single equation for the radial component of the gradient, which is proportional to the poloidal component of the magnetic field. The Shafranov shift can therefore be determined by solving:
. The Ф derivative can only vanish on the midplane, and this leaves again a single equation for the radial component of the gradient, which is proportional to the poloidal component of the magnetic field. The Shafranov shift can therefore be determined by solving: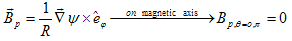
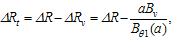
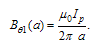
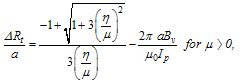
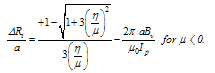
 , the plasma current
, the plasma current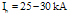 . Measurements of the plasma parameters were performed using single Langmuir probe, diamagnetic loop and a poloidally and toroidally oriented Mach probes. Theoretical models have been derived to describe the Mach probes data in un-magnetized and magnetized plasmas, using fluid, particle, and kinetic models (see the Figure (1)) [15-20]. Figure (2) shows the time dependence of the ion saturation currents collected by the poloidal Mach probes, the ratio of upstream to downstream current, and the resulting Mach number. The Mach number and thus the poloidal plasma velocity are obtained using the model of Hutchinson.
. Measurements of the plasma parameters were performed using single Langmuir probe, diamagnetic loop and a poloidally and toroidally oriented Mach probes. Theoretical models have been derived to describe the Mach probes data in un-magnetized and magnetized plasmas, using fluid, particle, and kinetic models (see the Figure (1)) [15-20]. Figure (2) shows the time dependence of the ion saturation currents collected by the poloidal Mach probes, the ratio of upstream to downstream current, and the resulting Mach number. The Mach number and thus the poloidal plasma velocity are obtained using the model of Hutchinson. 
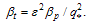
 produced by the circular plasma. Relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation [4]:
produced by the circular plasma. Relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation [4]: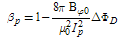
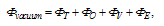

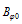 is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe,
is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe, 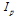 is the plasma current which can be obtained by the rogowski coil,
is the plasma current which can be obtained by the rogowski coil,  is the toroidal flux because of toroidal field coils,
is the toroidal flux because of toroidal field coils, 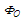 and
and 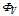 are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and
are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and 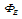 is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or fields discharge without plasma. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received (see Figure (3)). As shown in Eq. (23) the diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux
is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or fields discharge without plasma. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received (see Figure (3)). As shown in Eq. (23) the diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux 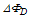 caused by plasma current can be measured from the diamagnetic and compensating coil using subtraction.
caused by plasma current can be measured from the diamagnetic and compensating coil using subtraction. 

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML


