Dengpan Zhang1, Jian Li1, Jiajia Yue1, Frank Härtig2, Hongliang Zhang1, Yibo Zheng1
1Institute of Precision Engineering, Henan Polytechnic University, Jiaozuo, China
2Physikalisch-Technischer Bundesanstalt (PTB), Braunschweig, Germany
Correspondence to: Dengpan Zhang, Institute of Precision Engineering, Henan Polytechnic University, Jiaozuo, China.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Gear is the key basic component of industrial equipment. Gear measurement has shown the characteristics of networking and cloud. In order to adapt to the rapid development of gear tooth surface measurement technology, this paper establishes a gear accuracy evaluation online service system based on cloud platform. The service provides different fitting algorithms for three-dimensional tooth surface deviation, realizes the three-dimensional visual expression of tooth surface deviation, and allows users to evaluate the whole tooth surface deviation of gear on line; In addition, the system realizes the standardization of gear measurement cloud data based on GXML data model, which is convenient for the storage and transmission of measurement results between different devices. Finally, the system saves the user's evaluation results in GXML data model and generates the corresponding detection report, which provides data support for the subsequent analysis of tooth surface deviation, improvement of gear manufacturing process and error traceability.
Keywords:
Three dimensional tooth surface deviation, GXML data model, Deviation evaluation algorithm, Test data set, Total tooth surface deviation
Cite this paper: Dengpan Zhang, Jian Li, Jiajia Yue, Frank Härtig, Hongliang Zhang, Yibo Zheng, Research on Construction Method of Gear 3D Surface Deviation Cloud Measurement System, Journal of Mechanical Engineering and Automation, Vol. 11 No. 1, 2022, pp. 1-8. doi: 10.5923/j.jmea.20221101.01.
1. Introduction
The three-dimensional deviation measurement of gear tooth surface is the latest development trend in the field of gear measurement, and has shown the characteristics of networking and cloud [1-2]. Developing a cloud measurement system for 3D tooth surface deviation measurement can not only realize the visual analysis of full tooth surface deviation and the cloud sharing of gear measurement data, but also provide data support for the traceability of gear manufacturing error.With regard to the research and application of cloud platform in the field of gear manufacturing and measurement, in order to standardize gear data, the German Institute of Engineers (VDE / VDI) has formulated the gear data exchange format GDE (gear data exchange format), which aims to realize the standardization of gear data format and solve the transmission problems caused by the heterogeneity of gear data [3-5]. On the basis of GDE, the German Federal Institute of Physics (PTB) proposed the gear digital calibration certificate (GDCC), which stores, authenticates and transmits the gear measurement and calibration results and signatures in the form of XML language. In 2015, PTB launched the international metrology software certification system (TraCIM) to implement metrology software traceability, aiming to realize the functions of requesting standard input data, submit ting results and obtaining certification reports in the certification process through a special network platform [6-7]. Based on the extensibility, structure and cross platform characteristics of XML language technology, Zhang dengpan et al. [8-9] proposed a standard language GXML for the field of gear measurement, and designed a cloud measurement system for gear measurement data exchange and three-dimensional tooth surface deviation evaluation. Tang Jie et al. [10] deployed a cloud processing system for processing gear double meshing measurement data on the cloud platform based on JavaWeb technology. The system transmits gear double-sided measurement related data in XML format, realizing the upload and download of measurement data on the cloud platform and the online evaluation of gear double meshing error. The above research contents study the measurement and expression of gear tooth surface deviation from the aspects of gear measurement data exchange format, tooth surface deviation evaluation system and gear measurement data cloud processing, but the contents of tooth surface deviation evaluation algorithm, three-dimensional visual expression of tooth surface deviation and application of GXML data model still need to be further studied.Aiming at the problem of mathematical modeling and visual expression of tooth surface deviation in three dimensional tooth surface deviation measurement, this paper develops a gear cloud measurement system based on Python web technology and GXML data model. The following sections introduce the system service process of the gear cloud measurement system in detail. Firstly, several fitting algorithms in the system are introduced from the mathematical background of the mathematical modeling algorithm of tooth surface deviation. Secondly, the system architecture and business logic of the gear cloud measurement system are introduced, and the functional modules in the system are described. Finally, the feasibility of the construction scheme of gear three-dimensional tooth surface deviation cloud measurement system is verified by using the actual tooth surface measurement data, which provides a new method and means for analyzing the whole tooth surface deviation, data sharing and error traceability. | Figure 1. System Service Framework |
2. Mathematical Background
The key requirement of three-dimensional tooth surface quality evaluation is to accurately fit and analyze the deviation of the gear tooth surface measurement point set. The point set data is generally the measurement point coordinate data and tooth surface point cloud data obtained from the gear surface through CMM or scanner. Its fundamental calculation goal is surface fitting. At present, the three-dimensional measurement technology of gear tooth surface is mainly three-dimensional surface reconstruction technology based on polynomial fitting method, B-spline surface method, NURBS surface fitting and Coons surface method, which correspond to different mathematical algorithms respectively. After completing the three-dimensional tooth surface deviation mathematical modeling, the deviation surface is analyzed to obtain the tooth pitch, tooth profile and other deviations of the tooth surface. This paper adopts the tooth surface deviation fitting algorithm based on 2D Chebyshev orthogonal polynomial, 2D Legendre orthogonal polynomial and bicubic B-spline [11]. Its mathematical background is described below.
2.1. Chebyshev Orthogonal Polynomial Fitting Algorithm
The concept of Chebyshev orthogonal polynomial fitting is used to obtain geometric features, which depends on its two advantages: one is that Chebyshev orthogonal polynomial can keep the maximum error to a minimum when used for fitting. The second is that the orthogonality of Chebyshev orthogonal polynomial can make it have no crosstalk during fitting, which is conducive to analyze the influence of different terms on the fitting results. The 2D Chebyshev orthogonal polynomial function image extended by 1D Chebyshev orthogonal polynomial has similar characteristics with common tooth surface deviation terms, so it is used for tooth surface deviation fitting.1D Chebyshev orthogonal polynomial 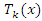 is shown in formula (1):
is shown in formula (1):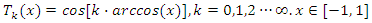 | (1) |
2D Chebyshev orthogonal polynomials can be generated by multiplying two 1D Chebyshev polynomials in the vertical direction, as shown in equation (2):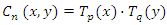 | (2) |
Where 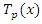 and
and 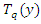 are 1D Chebyshev orthogonal polynomials along the x direction and y direction respectively. The definition domains are [-1,1], so the
are 1D Chebyshev orthogonal polynomials along the x direction and y direction respectively. The definition domains are [-1,1], so the 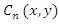 definition domain of is
definition domain of is 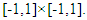 The tooth surface deviation function model constructed from the expression of the first n terms is shown in equation (3):
The tooth surface deviation function model constructed from the expression of the first n terms is shown in equation (3):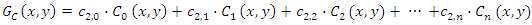 | (3) |
The full tooth surface deviation can be obtained from equation (3), and the deviation can be visually expressed by the system plug-in according to the function model. The three-dimensional tooth surface deviation fitting algorithm in the system is obtained from the programmed polynomial function model above. In addition, according to the corresponding characteristics of the first six polynomial function images with tooth pitch and tooth profile deviation, the corresponding term coefficients can be used to evaluate the common tooth surface deviation terms.
2.2. Legendre Orthogonal Polynomial Fitting Algorithm
Legendre orthogonal polynomials and Chebyshev orthogonal polynomials have similar characteristics. Because they can keep the maximum error to the minimum and the orthogonality between items, they can be applied to deviation surface fitting. 1D Legendre orthogonal polynomials are also a set of orthogonal function systems defined in the range of [-1,1], 1D Legendre equation is expressed as equation (4):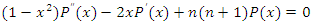 | (4) |
When n is an integer, 1D Legendre polynomial is a special solution of 1D Legendre equation, where m = n / 2 when n is an even number; When n is an odd number, m= (n-1) / 2; 1D Legendre polynomial is shown in equation (5):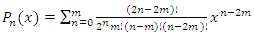 | (5) |
2D Legendre orthogonal polynomial can be extended from two 1D Legendre orthogonal polynomials, that is, it is obtained by multiplying two 1D Legendre polynomials 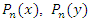 in the vertical direction. Its definition domain is on the [-1,1]×[-1,1] rectangular region. The expression of the first n terms of the 2D Legendre orthogonal polynomial is shown in equation (6):
in the vertical direction. Its definition domain is on the [-1,1]×[-1,1] rectangular region. The expression of the first n terms of the 2D Legendre orthogonal polynomial is shown in equation (6):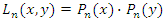 | (6) |
2D Legendre orthogonal polynomials are defined in the [-1,1]×[-1,1] domain. The tooth surface can be regarded as a rectangular surface in the tooth surface coordinate system. After normalizing the tooth surface to the [-1,1]×[-1,1] domain, 2D Legendre orthogonal polynomials are used for deviation function modeling. The tooth surface deviation function model constructed by the first n terms of the polynomial in equation (6) in the system is shown in equation (7):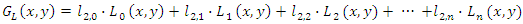 | (7) |
In the gear cloud measurement system, after the tooth surface deviation function model established based on equation (7) is programmed, it is the three-dimensional tooth surface deviation fitting algorithm based on Legendre orthogonal polynomial in the system. After the system drawing, the plug-in processing function model can directly display the whole tooth surface deviation, and the common tooth surface deviation items can also be evaluated according to the corresponding term coefficients of the first six items.
2.3. Bicubic B-spline Fitting Algorithm
Bicubic B-spline fitting algorithm can better deal with the surface fitting problem of scattered points in engineering application. It constructs bicubic B-spline surface equation according to control vertices and basis function. If N = (m+1) 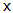 (n+1) control vertices
(n+1) control vertices 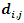 (i=0,1,2⋯m, j = 0,1,2⋯n ) are known, k and l are the times of parameters u and v, the two node vectors are:
(i=0,1,2⋯m, j = 0,1,2⋯n ) are known, k and l are the times of parameters u and v, the two node vectors are: 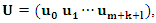
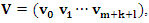 Then the B-spline surface equation is shown in equation (8):
Then the B-spline surface equation is shown in equation (8):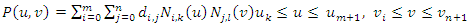 | (8) |
Where 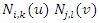 is a spline basis function, and the basis function is shown in equation (9):
is a spline basis function, and the basis function is shown in equation (9):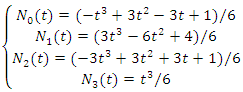 | (9) |
When k=l=3, equation (8) is the bicubic B-spline surface equation.Based on the three-dimensional tooth surface deviation fitting algorithm described in 2.1-2.3, the algorithm is realized through the cloud system, and the cloud 3D evaluation service is provided. The user completes the gear measurement through the measuring equipment, preprocesses according to the data format, submits the data through the user terminal, and the cloud system completes the three-dimensional reconstruction of the tooth surface deviation surface. The function model established by the algorithm can comprehensively analyze the whole tooth surface deviation. In addition, according to the three-dimensional tooth surface deviation function model, the order discussion of tooth surface deviation can analyze the error sources in manufacturing and be used to improve the subsequent manufacturing process.
3. Construction and Implementation of Gear Cloud Measurement System
3.1. Gear Cloud Measurement System Architecture
The gear cloud measurement system is built based on Python web framework and uses GXML data model to save, exchange and transmit gear measurement deviation data [12]. First, create an application under the Django project through the Django admin management tool for local development. The system front-end interface is developed based on HTML and CSS, and python provides computing support for the system background. The local development is completed in Pycharm, and the Django and Numpy third-party packages required for the project are downloaded and installed through the python package management tool pip. The system front-end interface framework is supported by Bootstrap framework, and the three-dimensional tooth surface deviation drawing is completed by Echarts and Matplotlib plug-ins. The deviation data generated by uploading and calculation in the system are saved in the database after being standardized by GXML data model. When generating the test report, you can call the corresponding GXML document in the database. Finally, upload the locally developed system to the cloud server to provide services for users. The system architecture and technical scheme of gear cloud measurement system are shown in Figure 2.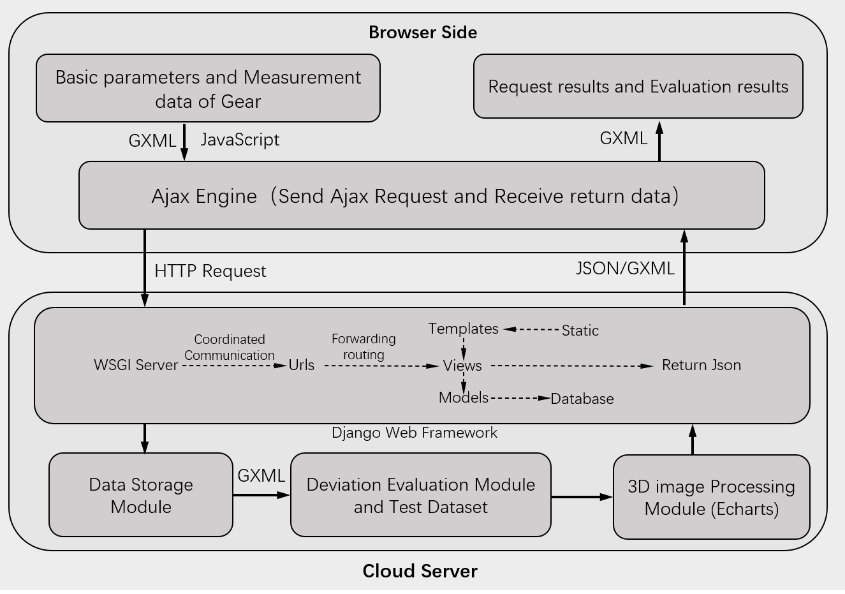 | Figure 2. System Architectures |
3.2. GXML Data Model
Gear extensible markup language (GXML) is a standardized data exchange format for expressing and storing gear measurement results in the cloud. It is an expansion of XML language in the field of gear measurement [13-14]. The gear cloud measurement system realizes the standardized processing of gear measurement deviation data through GXML. The system generates GXML documents through the data model based on GXML standardized data exchange format, which makes the gear measurement data in XML format more unified in format and content. GXML data model ensures that both sides of data exchange have the same data format, so that gear measurement deviation data can be exchanged directly. The structure of GXML data model [15-17] is shown in Figure 3. | Figure 3. GXML Data Model Structure |
3.3. 3D Tooth Surface Deviation Measurement Service Logic
The main user objects of the gear cloud measurement system are the gear measurement mechanism and the research institution of 3D gear tooth surface deviation evaluation algorithm. The 3D tooth surface deviation measurement service in the system can enable them to obtain the tooth surface deviation quickly and intuitively. The calculation of three-dimensional tooth surface deviation measurement service partially depends on Django's MTV framework as shown in Figure 2. After registering and logging in, you can first access the gear measurement module in the gear cloud measurement system through the front page of the system or URL address. After uploading the corresponding gear measurement point data and gear basic parameters in the gear measurement module, the gear basic parameters will be standardized and saved to the database in GXML format as shown in Figure 4. Click Submit to send the Ajax request from the front end, resolve the routing address by the Urls file, then forward to the corresponding Views, call the algorithm program in Views to complete the calculation of the three-dimensional tooth surface deviation. The calculated results need to be returned to the front-end interface, and the front-end Echarts executes the drawing program, and saves the calculated results into the database in the form of GXML document for subsequent download services. | Figure 4. Basic Parameters of Gear in GXML Format |
3.4. Test Data Set Download
For evaluation algorithm research institutions, the original data of tooth surface measurement points need to be used when testing and developing new evaluation algorithms. The test data set provided by the gear cloud measurement system contains the original data of tooth surface measurement points. The test data set is composed of many tooth surface measurement point data, including the XYZ coordinate value of each measurement point and the corresponding deviation of this point. Users can access the Url address to obtain the corresponding service of the test dataset. During execution, the request is forwarded to the corresponding test data set download interface from the Urls address file in Django, and the corresponding test data set file is retrieved from the system database. The test data set in the gear cloud measurement system is normalized by the GXML data model into a GXML document as shown in Figure 6, where x_ axis, y_ axis, z_ axis is the coordinate value of a single tooth surface measurement point. In addition, the corresponding reference results are included, and researchers can compare the calculated results with the reference results. The test data set currently provided is measured by CMM as shown in Figure 5. | Figure 5. Experimental CMM |
 | Figure 6. GXML Format Test Data set |
3.5. GXML Test Report Download
When the user uses the gear cloud measurement system to measure the 3D tooth surface deviation, after correctly uploading the data to the system, the system will give the corresponding deviation evaluation results [18] and create the test report according to the three-dimensional tooth surface deviation evaluation algorithm in the system. The detection results returned by the system from the database are included in a GXML data document as shown in Figure 7 [19-20], and then parsed into an easy to read PDF file. | Figure 7. GXML Document of Test Report |
4. Application Experiment of Gear Cloud Measurement System
4.1. 3D Tooth Surface Deviation Expression Modules
The 3D tooth surface deviation expression module of gear cloud measurement system aims to intuitively express the deviation of the whole tooth surface. After completing the system registration login, correctly entering the basic gear parameters and importing the tooth surface measurement point data in the lower input box, click "calculate", the system will complete the deviation modeling according to the currently selected 3D tooth surface deviation modeling algorithm, and the results will be visually displayed in the front end of the system. The deviation of 1R tooth surface is shown in Figure 8: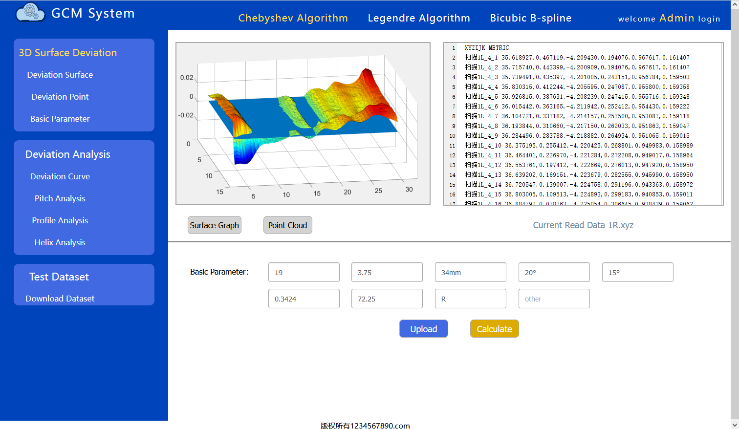 | Figure 8. 3D Surface Deviation Expression Module |
4.2. Full Tooth Surface Deviation Analysis Module
The whole tooth surface deviation analysis module in the system aims to comprehensively analyze the gear tooth surface according to the deviation function model established in 2, that is, analyze profile and helix at any place. As shown in Figure 9, the module of the system first carries out the solid modeling of the gear according to the basic parameters of the gear by the OpenjsCAD plug-in. Secondly, it realizes the visual expression of the pitch deviation of any tooth and the deviation of tooth profile and helix of any tooth surface.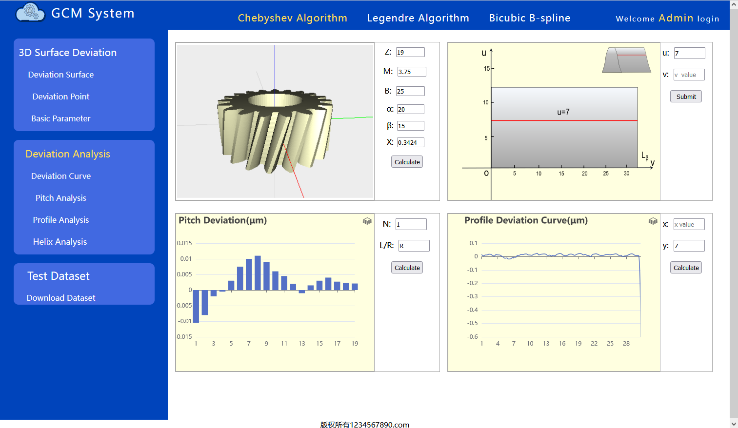 | Figure 9. Full Surface Deviation Analysis Module |
4.3. Test Report and Test Data Set Download Module
The test data set and test report download module in the gear cloud measurement system provides test data set and report document download services. As shown in Figure 10, for the researchers of three-dimensional tooth surface deviation algorithm, they can directly download the required data on this page to test the effect of the algorithm, so as to realize testing while developing and improve the development efficiency. For error traceability researchers, the historical report in the system can be downloaded for error traceability analysis.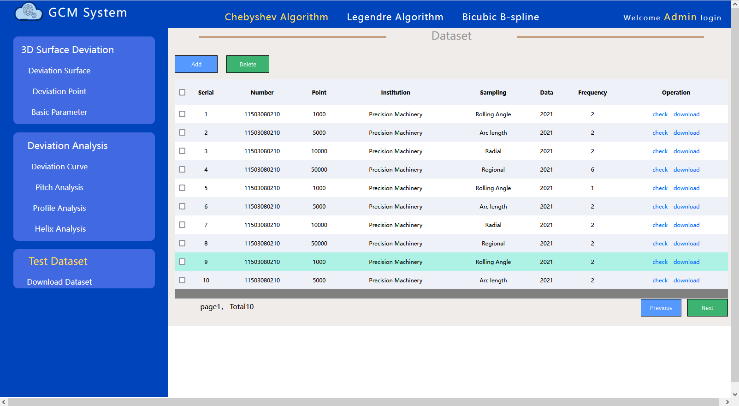 | Figure 10. Test Dataset Download Module |
5. Conclusions
The gear cloud measurement system is built based on Python Web framework and GXML data model, which aims to provide services for gear measurement mechanism and 3D tooth surface deviation evaluation algorithm research organization. The system contains built-in three-dimensional tooth surface deviation evaluation algorithms, which can mathematically model the tooth surface deviation, evaluate the whole tooth surface deviation of the gear, and visually express the evaluation results in three dimensions.The system provides a test data set based on GXML data model, which can be used for Algorithm Engineers to test their own three-dimensional tooth surface deviation evaluation algorithm, and the system provides the reference results of the test data set for comparison, which is convenient for engineers to test when developing.The gear cloud measurement system will save the user's test data and test results in the form of GXML document and provide the download of test report for analyzing the error of gear manufacturing process and subsequent improvement of gear manufacturing process.
ACKNOWLEDGEMENTS
This project is supported by National Natural Science Foundation of China (No. 51775174, No. 51635001).
References
| [1] | M.S. Al-Asaly, M.M. Hassan, and A. Alsanad, “A cognitive/intelligent resource provisioning for cloud computing services: opportunities and challenges,” Soft Computing, vol. 23, pp. 9069-9081, October 2019. |
| [2] | A.E. Eshratifar, M.S. Abrishami, and M. Pedram, “JointDNN: an efficient training andinference engine for intelligentmobile cloud computing services,” IEEE Transactions on Mobile Computing, vol. 20, pp. 565-576, February 2021. |
| [3] | VDI 2610:2014 Exchange format for gear data-gear data exchange format (GDE format)-definition -corrigendum concerning standard [S]. |
| [4] | G Gravel. A Günther. Gear data exchange format [J]. Gear technology. 2005. 22(2): 36-40. |
| [5] | A. Günther, K. Kniel, F. Härtig. Introduction of a new bevel gear measurement standard [J]. CIRP Annals-Manufacturing Technology, 2013. 62(1): 515-518. |
| [6] | F. Härtig, J. Tang, D. Hutzschenreuter, Online validation of comparison algorithms using the TraCIM-system [J]. Int J MechEngAutom Volume 2, Number 7, 2015: 312-327. |
| [7] | D. Hutzschenreuter, F Härtig, Klaus Wendt. Online Validation of Chebyshev Geometric Element Algorithms Using the TraCIM-System [J]. Journal of Mechanical Engineering and Automation 2015, 5(3): 94-111. |
| [8] | Y. Wang, X.J. Yao, H.L. Zhang, R.T Liu, L.Y. Wang, and D.P. Zhang, “Study on gear measuring data definition and it’s exchange method based on cloud platform,” Journal of Henan Polytechnic University (Natural Science), vol. 40, pp.105-110, January 2021. |
| [9] | D.P Zhang, J.J Yue, J.L, etl. Gear Cloud Measurement Digital Platform Based on XML [J]. International Journal of Trend in Research and Development, 2021; Vol. 8(4). |
| [10] | J. Tang, R.Z Zhang. Z.Y. Shi. Deployment and Implementation of data cloud processing system for double-flank gear rolling test based on Javaweb [J]. Optical Precision Engineering. 2021, 29(06): 1387-1396. |
| [11] | G. Goch, K. Ni, Y. Peng, A. Güenther. Future gear metrology based on areal measurements and improved holistic evaluations [J]. CIRP Annals –Manufacturing Technology 2017; 66, Vol. 1: 469-474. |
| [12] | Milanovic N, Malek M. Current solutions for Web service composition [J]. IEEE Internet Computing, 2004, 8(6): 51-59. |
| [13] | C. H. Huang, T. R. Chuang, D.P. Deng and H.M. Lee, ” Building GML-native web-based geographic information systems,” Computers & Geosciences, vol. 35, pp. 1802-1816, September 2009. |
| [14] | J. Downing, P. Murray-Rust, A.P. Tonge, P. Morgan, H.S. Rzepa, and F. Cotterill, et al, “SPECTRa: the deposition and validation of primary chemistry research data in digital repositories,” Journal of Chemical Information and Modeling, vol. 48, pp. 1571-1581, August 2008. |
| [15] | W. Phadungsukanan, M. Kraft, J.A Townsend, and P. Murray-Rust,” The semantics of Chemical Markup Language (CML) for computational chemistry: Comp Chem,” Journal of Cheminformatics, vol. 4, August 2012. |
| [16] | S. Kim, S. Yang and Y. Ko, “Classifying mathematical expressions written in MathML,” IEICE Trans. Inf. & Syst., vol. E95-D, pp.2560-2563, October 2012. |
| [17] | M.Q. Nghiem, G.Y. Kristianto, and A. Aizawa, “Using MathML parallel markup corpora for semantic enrichment of mathematical expressions,” IEICE Trans. Inf. & Syst., vol. E96-D, pp.1707-1715, August 2013. |
| [18] | T.C. Zhang. Gear inspection 500 questions [M]. China Standards Press. 2007. |
| [19] | Fong J, Pang F, Bloor C. Converting Relational Database into XML Document [M]. 12th International Workshop on Database and Expert Systems Applications. Munich. 2001: 61-65. |
| [20] | Chaudhria B, Rashid A, Zicari R. XML Data Management: Native XML and XML-enabled Database Systems [M]. Addison Wesley. 2003: 90-91. |




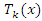 is shown in formula (1):
is shown in formula (1):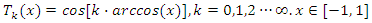
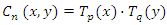
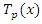 and
and 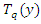 are 1D Chebyshev orthogonal polynomials along the x direction and y direction respectively. The definition domains are [-1,1], so the
are 1D Chebyshev orthogonal polynomials along the x direction and y direction respectively. The definition domains are [-1,1], so the 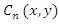 definition domain of is
definition domain of is 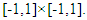 The tooth surface deviation function model constructed from the expression of the first n terms is shown in equation (3):
The tooth surface deviation function model constructed from the expression of the first n terms is shown in equation (3):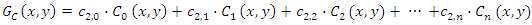
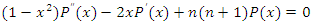
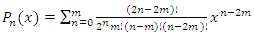
 in the vertical direction. Its definition domain is on the [-1,1]×[-1,1] rectangular region. The expression of the first n terms of the 2D Legendre orthogonal polynomial is shown in equation (6):
in the vertical direction. Its definition domain is on the [-1,1]×[-1,1] rectangular region. The expression of the first n terms of the 2D Legendre orthogonal polynomial is shown in equation (6):
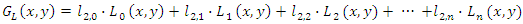
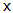 (n+1) control vertices
(n+1) control vertices 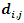 (i=0,1,2⋯m, j = 0,1,2⋯n ) are known, k and l are the times of parameters u and v, the two node vectors are:
(i=0,1,2⋯m, j = 0,1,2⋯n ) are known, k and l are the times of parameters u and v, the two node vectors are: 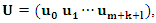
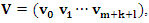 Then the B-spline surface equation is shown in equation (8):
Then the B-spline surface equation is shown in equation (8):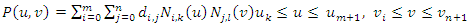
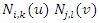 is a spline basis function, and the basis function is shown in equation (9):
is a spline basis function, and the basis function is shown in equation (9):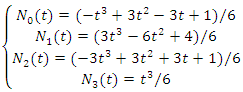









 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML