Sujan Rao Nakkanti1, Radhakrishna M.2, AMK Prasad3
1Department of Mechanical Engineering, Sai Spurthi Institute of Technology, Sathupally, Telangana, India
2Mechanical Design & Engineering Department, CSIR-Indian Institute of Chemical Technology, Hyderabad, India
3Department of Mechanical Engineering, University College of Engineering (A), OU, Hyderabad, India
Correspondence to: Radhakrishna M., Mechanical Design & Engineering Department, CSIR-Indian Institute of Chemical Technology, Hyderabad, India.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Bellows expansion joints are widely used in the piping system to take care of any expansion and contraction that the pipe undergoes due to variations in temperature and pressure. It is often observed that piping systems in industrial plants are often subjected to deformation caused by thermal expansion, vibrations from rotating machinery and improper location of pipe supports. It is a practice to install Polytetrafluoroethylene (PTFE) expansion bellows in all such applications, as they have the ability to absorb expansion and shocks. The influence of pressure and end conditions of metallic bellows has been dealt by researchers in the past. However, very scanty information is available and is propriety, on vibrations of PTFE bellows. The influence of pressure and temperature on vibrations of PTFE bellows expansion joint, forms the basis of the present study. A mathematical model is developed for PTFE bellows expansion joint installed in a pipeline carrying fluid by considering the end conditions as fixed. The bellows are treated both as a Timoshenko beam model. Analytical results are obtained for combined effect of pressure and temperature on the frequency and were found to be significant. The transcendental equation for estimation of transverse vibrations of bellows is derived using the Hamilton’s Variation Principle and energy expressions. It is observed that as the fluid pressure and temperature increases, the transverse vibrations of PTFE bellow decrease. The frequencies for four modes of vibration were validated by conducting experiments on a PTFE bellow installed in the pipeline and fluid conveying (water) at different pressures and temperatures. The results are found to be in good agreement.
Keywords:
Transverse vibrations, PTFE bellows, Timoshenko beam, Pressure and thermal loads
Cite this paper: Sujan Rao Nakkanti, Radhakrishna M., AMK Prasad, Influence of Pressure and Thermal Loadings on Transverse Vibrations of Polytetrafluoroethylene Bellows Expansion Joint, Journal of Mechanical Engineering and Automation, Vol. 8 No. 2, 2018, pp. 49-58. doi: 10.5923/j.jmea.20180802.02.
1. Introduction
In recent times, non-metallic bellows expansion joint has been found to be more compatible with many potential industrial applications, particularly in piping systems for fluid conveying. This is because of its good mechanical, chemical and thermal properties at par with any metallic expansion joint. Several types of continuum-based elasticity theories were modeled as an elastic corrugated cylindrical tube representing a bellows expansion joint, and the mechanics and dynamic response of bellows expansion joint were studied. The Euler-Bernoulli and the Timoshenko beam theory have been employed to investigate structural properties of bellows expansion joints for stress-strain relationship, buckling, and wave characteristics. Several researchers have employed the continuum-based theories to study the vibration behavior of metallic bellows expansion joins filled with fluid. Anderson [1, 2] used the asymptotic solution given by Clark [7], to develop solutions for deflection stresses in U-shaped bellows. He also introduced corrections to compensate for the approximations suggested by Clark [7]. Gerlach, C. R [9] studied the influence of internal moving fluid as flow induced vibrations of metal bellows based on a continuum elastic model. In 1972, Bass and Holster [6] extended the work of Gerlach to study the vortex excitation of metallic bellows with internal cryogenic flows. It was found that internal cavitation or boiling due to heat transfer in the formation of frost or condensation on outside of bellows convolutions had the effect of damping the vibrations. Azar.R.C, Chadrashekar.S, and Szaban.P [3] developed a computer program in determining the axial vibrations of metallic bellows to improve the performance of bellows by altering the spread of its natural frequencies thereby avoiding resonance. They argued that the earlier techniques for determining the bellows stiffness use either the beam theory or the theory of plates and shells. The first approach, according to them was over simplification while the second method derives equations that are difficult to use. Hence, they derived equations based on the Curved Beam Theory. The computer program developed by them uses the Holtzer method in determining the natural frequencies and mode shapes for the axial vibration. In 1986, The EJMA [4] also provided a simplified method for calculating the natural frequencies of bellows. The approach followed by EJMA is on the assumption that bellows can be considered as a continuous elastic rod. Becht [5] has brought out an excellent survey of the developments of numerical and theoretical methods for predicting the response of bellows. The state-of-the–art was assessed to cover the earlier work of 1940 and that the directions requiring further development were discussed. Rockwell and Naudascher [8] in their review work suggested that the actual excitation mechanism in the bellows is probably the free shear layer instability over the periodic cavities created by the bellows convolutions. Li et al. [10] developed equations that are used to calculate the axial and lateral natural frequencies of a single bellow with three types of end connections. Jakubauskas et al. [11-13] examined the axisymmetric axial vibrations and in-fluid, natural frequencies by considering the effect of added mass for Metallic bellows expansion joint (MBEJ) bellows mode. Added mass influence was studied at the transverse rigid body motion and distortion of the convolution bending, and developed an analytical expression in the form of Rayleigh quotient, suitable for determination of transverse natural frequencies. Broman et al. [14] examined and developed a procedure determining the dynamic characteristics of bellows by using certain parameters of the beam using I-DEAS. Radhakrishna M et al. [15, 16] studied the transverse vibrations of bellows with elastically restrained end conditions. The present paper applies the Timoshenko beam theory, to study the influence of pressure and temperature on the fundamental frequency of fluid conveying PTFE bellows expansion joint with fixed boundary conditions.
2. Mathematical Model and Analysis
A schematic diagram of a PTFE bellows expansion joint embedded in elastic medium with the two ends fixed for conveying fluid, is considered as a hollow corrugated tube as shown in Fig. 1. The transverse displacement ‘w’ of the PTFE bellows expansion joint is dependent on time- ‘t’ and the spatial coordinate-‘s’.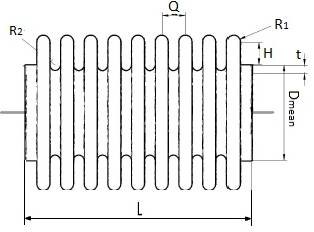 | Figure 1. Geometry of bellows expansion joint |
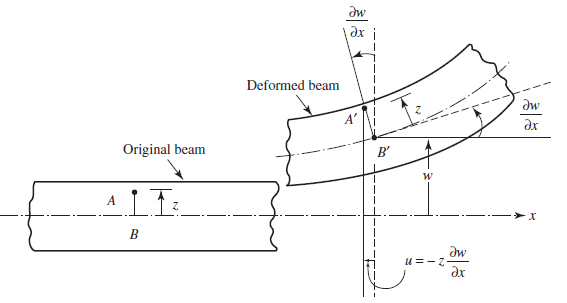 | Figure 2. Bending of the beam element |
Here 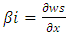 is shear deformation or shear angle in Fig. (3)(a). The fibers are located in an element at a distance as a ‘z from the centerline. The shear deformation has no effect to cause any axial displacement. Hence, the components of displacement can be expressed as
is shear deformation or shear angle in Fig. (3)(a). The fibers are located in an element at a distance as a ‘z from the centerline. The shear deformation has no effect to cause any axial displacement. Hence, the components of displacement can be expressed as 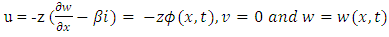 | (1) |
The PTFE bellows expansion joint has an equivalent bending rigidity EI and length L with the crown and root radii of R1 and R2 and a thickness, t [3-5]. The governing equation of motion for free vibration of the fluid-conveying pipe is derived by applying the Timoshenko elastic theory. 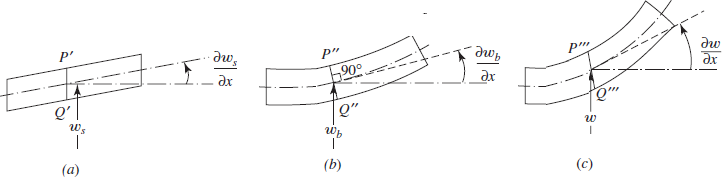 | Figure 3. Beam elements with (a) shear, (b) bending and (c) total deformation |
The components of stress and strain are represented using the displacements as given in equation (1).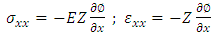 | (2) |
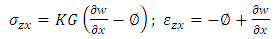 | (3) |
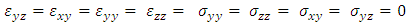 | (4) |
The strain energy of the system is expressed as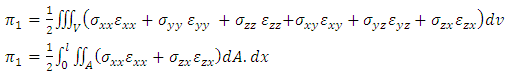 | (5) |
On the substitution of equations 2, 3 and 4 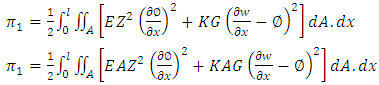 | (6) |
Equation (6) is written as 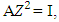 where I is the moment of inertia of the bellow
where I is the moment of inertia of the bellow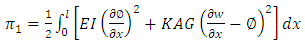 | (7) |
Strain energy due to Pressure,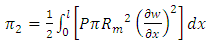 | (8) |
The Stain energy due to temperature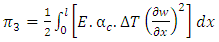 | (9) |
In adding of equations 6, 7, 8 and 9 the total strain energy equation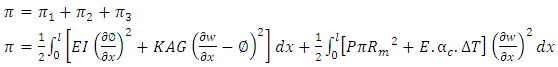 | (10) |
Kinetic energy is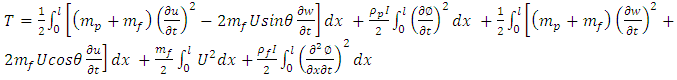 | (11) |
Now eliminating non-linear terms and 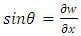
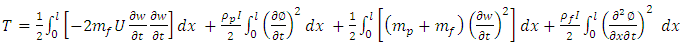 | (12) |
Applying the virtual work principle, we have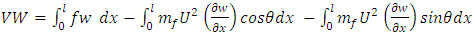 | (13) |
And elimination of non-linear terms and 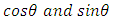
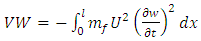 | (14) |
Substituting in Hamilton Principle gives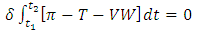 | (15) |
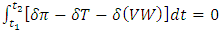 | (16) |
Consider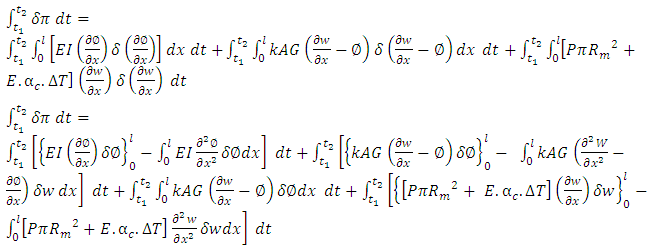 | (17) |
The Kinetic Energy term is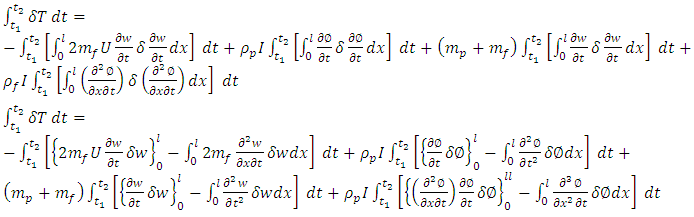 | (18) |
Consider the virtual work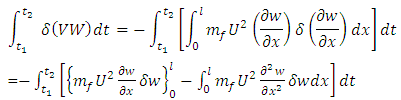 | (19) |
On substitution of 17, 18, and 19 in 16 gives 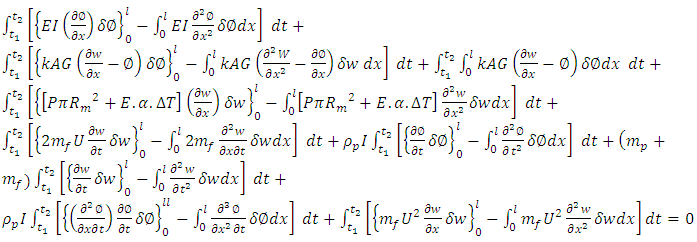 | (20) |
Now considering terms 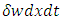
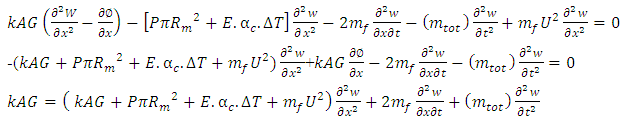 | (21) |
Divide with kAG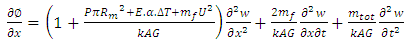 | (22) |
Now consider term 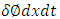
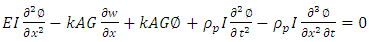 | (23) |
The equation (23), on differentiation with respect to dx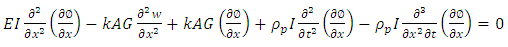 | (24) |
On substitution of 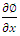 in equation (24), we get
in equation (24), we get 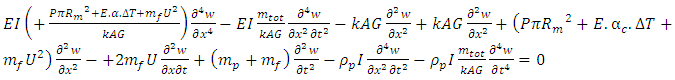 | (25) |
Eliminating non-linear terms 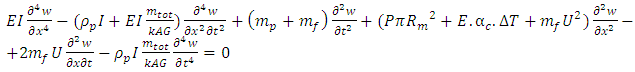 | (26) |
Now, boundary conditions with respect to 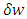
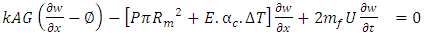 | (27) |
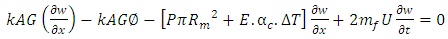 | (28) |
In equation (26) the rotary inertia and shear is calculated as 5.2508e-11 and 0.7615e-3 respectively. As the shear component is very negligible, it has been neglected. Similarly, the effect of fluid velocity up to 10 m/sec [3] for a short beam has also been neglected. The equation (26) can be rewritten as-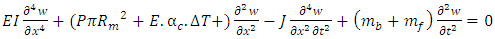 | (29) |
Where EI, P, T, E, J, w, x, mb, mf are bending stiffness, pressure, temperature, modulus of elasticity, total mass moment of inertia per unit length, deflection, axial coordinate, the mass of bellow and the mass of the fluid.According to Y. Yan et al. [17] the dimensionless parameters are defined as follows. The magnitude of the dimensionless numbers indicates the relative effect of pressure and temperature on the system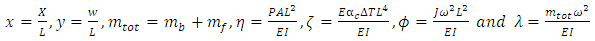 | (30) |
According to Jakubauskas et al. [12] divide the Equation. (29) with EI and substitute equation (30), the governing differential equation of motion can be reduced to the following the dimensionless form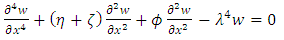 | (31) |
Using the technique of separation of variables, the lateral deflection of the bellows axis ‘w’ can be expressed as 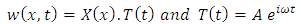 | (32) |
Differentiating the above equation (30) and substituting into the differential equation (31) we get,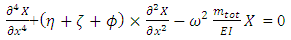 | (33) |
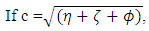 | (34) |
Then equation (33) can be written as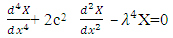 | (35) |
Assuming a general solution of the equation (35) is given by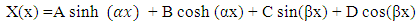 | (36) |
Where A, B, C, D are arbitrary constants respectively. The first two derivatives of the equation (36) are as follows 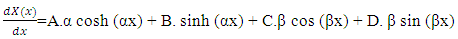 | (37) |
Let the roots of the equation (37) be α & β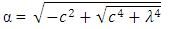 | (38) |
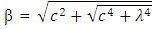 | (39) |
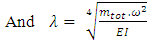 | (40) |
The fixed-fixed boundary conditions are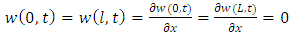 | (41) |
The boundary conditions given by the Equation. (41) corresponding to conditions of zero displacement and zero slope at x = 0 and x = L respectively.The solution of the differential equation (35) can be expressed as 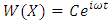 | (42) |
Where 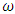 is circular frequency and C is arbitrary constant.On substitution of Equation. (41) in Equation. (37) the following equation is obtained
is circular frequency and C is arbitrary constant.On substitution of Equation. (41) in Equation. (37) the following equation is obtained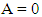 | (43) |
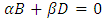 | (44) |
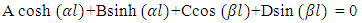 | (45) |
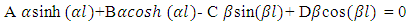 | (46) |
Determinate for the above four equations 43, 44, 45 and 46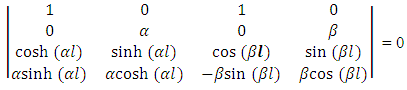 | (47) |
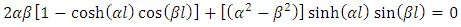 | (48) |
Equation (48) is closed form the transcendental equation for finding the natural frequencies of transverse vibration of single bellow expansion joint. Using the Muller’s bisection method the characteristic equation (48) is solved for four modes of vibration.
3. Results and Discussion
In this paper, the free vibration equation of the fluid conveying PTFE bellows expansion joint is derived by using Timoshenko elastic theory. The results are obtained by analyzing the effect of pressure and combined effect of pressure and temperature of the fluid (water) on the frequencies at different modes.
3.1. Frequency with Change of Inlet Pressure
Table 1 presents the influence of pressure variation on the four modes of vibration. The frequencies are obtained in non-dimensional form. Table 1 and Figure 4 represent the change of frequency with respect to inlet pressure. Bellows become unstable at critical pressure when the non-dimensional frequency becomes zero. It is found that the critical pressure of bellows approaches 13 for first mode, 26 for second mode, 49 for third mode and 73 for fourth respectively. It is found that the bellows are instable.Table 1. Fundamental natural frequencies for varying inlet pressure
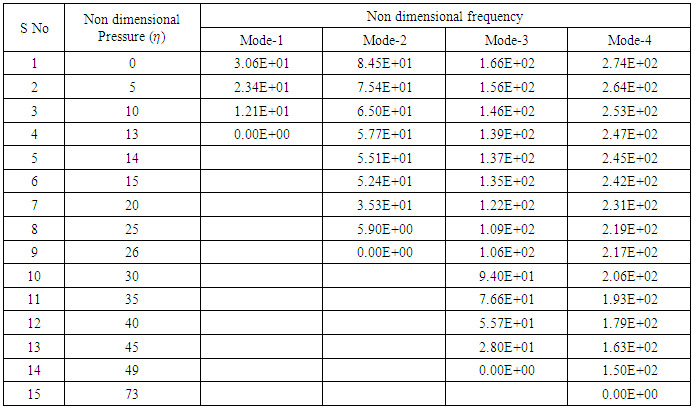 |
| |
|
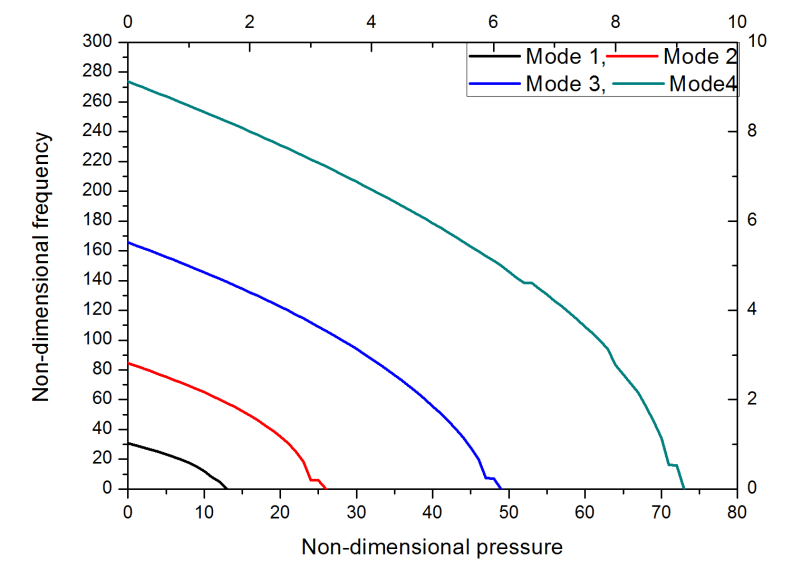 | Figure 4. Frequency for fur modes by varying of inlet pressure |
Table 2 and Figure 5 present the fundamental mode frequency of the PTFE bellow at different pressures. It is seen that as the temperature increases for a particular value of pressure, the frequency decreases. At a pressure of 1 unit and non-dimensional temperature term parameter 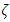 = 18, the fundamental mode frequency is 1.789; whereas, at a pressure of 10 units and
= 18, the fundamental mode frequency is 1.789; whereas, at a pressure of 10 units and 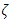 =2, the frequency is 7, which amounts to a decrease of around 74%. It can be inferred that with a change in temperature, there is every likelihood of occurrence of failure of the bellow, for a rise in pressure. This also concludes that the bellow can prematurely fail, even before attaining the required design temperature.
=2, the frequency is 7, which amounts to a decrease of around 74%. It can be inferred that with a change in temperature, there is every likelihood of occurrence of failure of the bellow, for a rise in pressure. This also concludes that the bellow can prematurely fail, even before attaining the required design temperature.Table 2. Fundamental Mode Frequency at different temperatures and pressures
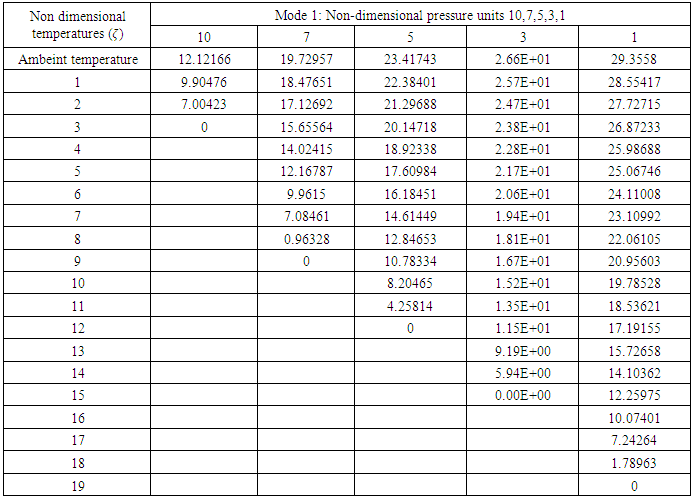 |
| |
|
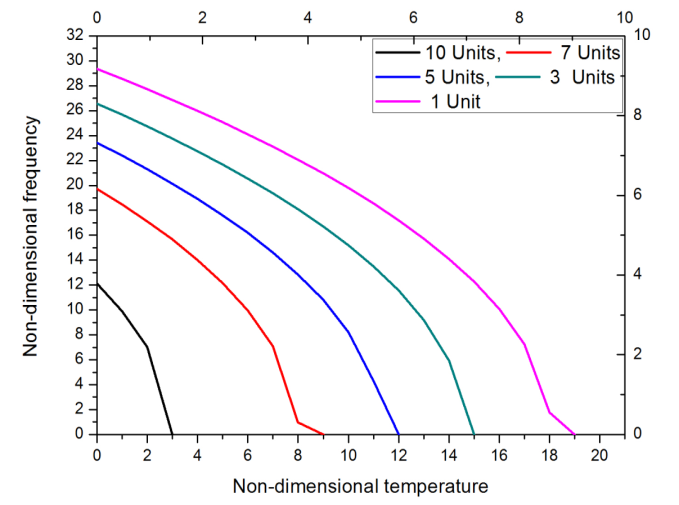 | Figure 5. Frequency of mode 1 for variation in temperature and different pressures |
3.2. Frequencies for Combined Effect of Pressure and Temperature for other Modes
Figure 6 presents the frequency for Mode 2 vibration of the PTFE bellow at different inlet pressures. It is observed that as the temperature increases for a particular value of pressure, the frequency decreases. At a pressure of 1 unit and non-dimensional temperature term parameter 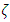 = 38, the frequency obtained is 11.33; at a pressure of 10 units and
= 38, the frequency obtained is 11.33; at a pressure of 10 units and 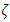 =23, the frequency is 10.768, which amounts to a decrease of around 4%. It is also found that with an increase of pressure term,
=23, the frequency is 10.768, which amounts to a decrease of around 4%. It is also found that with an increase of pressure term, 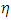 =1 to
=1 to 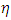 = 3 the temperature term decreases, from
= 3 the temperature term decreases, from 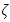 = 39 at
= 39 at 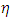 =1 and
=1 and 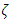 = 36 at
= 36 at 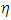 = 3, which is a reduction of 7% in change of frequency.
= 3, which is a reduction of 7% in change of frequency. 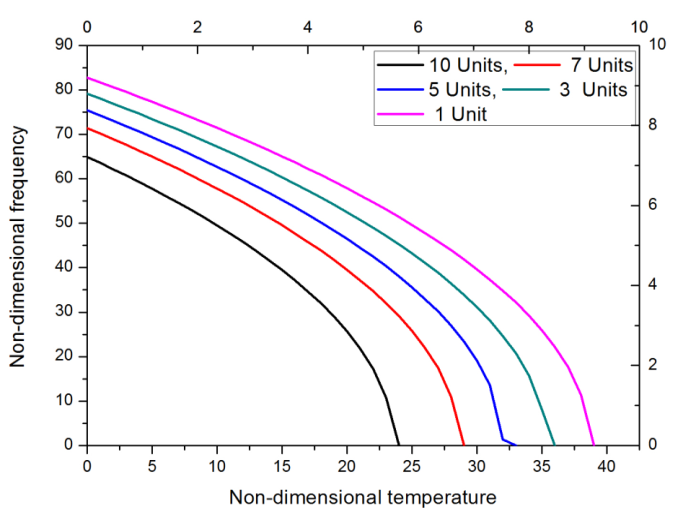 | Figure 6. Frequency for mode 2 of vibration variation in temperature and different pressures |
This implies that there is a possibility of failure of the bellow with respect to change in temperature. This is applicable to other modes of vibration 3 and 4, as shown in figures 7 & 8 respectively.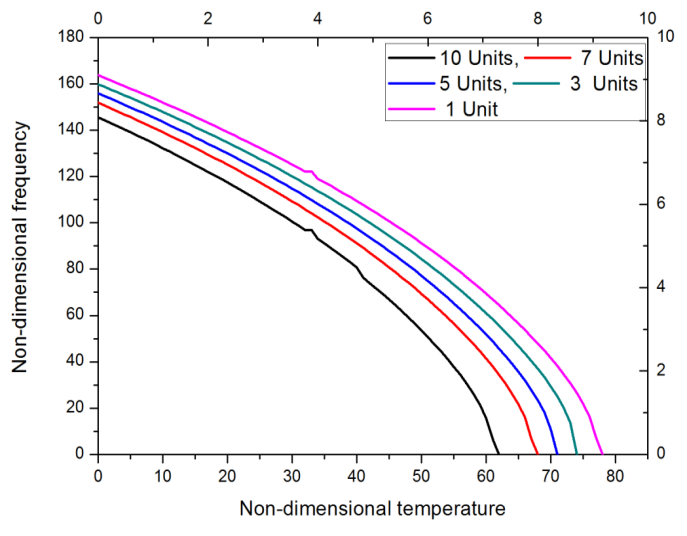 | Figure 7. Frequency for mode 3 of vibration variation in temperature and different pressures |
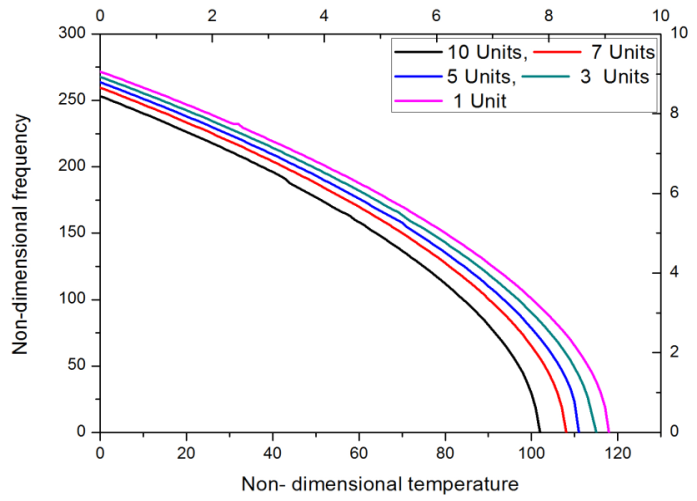 | Figure 8. Frequency for mode 4 of vibration variation in temperature and different pressures |
3.3. Comparison of Theoretical and Experimental Results
The experimental setup consists of 80mm outer diameter PTFE bellow which is fixed at both ends and connected with pipes for fluid flow. A globe valve is used to regulate inlet pressure and pressure gauges and thermocouples are mounted to measure the inlet and outlet pressures and temperatures. A Piezoelectric transducer (Accelerometer) is installed on the bellow at different positions to obtain frequencies in terms of velocity and displacement. The Vibration analyzer, signal records the waveform. Properties of PTFE bellow for comparing theoretical results are given below:Density of PTFE bellows expansion joint is 2300 kg/m3; bending rigidity 4.4692 NM; the mass of the fluid in the bellow per unit length is 2.859 kg and the mass per unit length is 3.7718 kg. Geometric and material parameters: diameter of bellow, Dm = 80.0mm; thickness of bellow, tp = 2mm; Pitch of bellow, q = 5mm; length of bellow, L = 32.1mm; convolution height of bellow, h = 5.71 mm; Young’s modulus of the bellows, 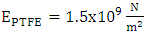 ; Root and crown radius R1 =
; Root and crown radius R1 = 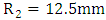 ; Coefficient of thermal expansion
; Coefficient of thermal expansion 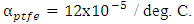 Table 3, figures 9 and 10 represent a comparison and validation of results found by theory and experiments. It is observed that at
Table 3, figures 9 and 10 represent a comparison and validation of results found by theory and experiments. It is observed that at 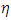 = 1.0 and
= 1.0 and 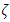 =0 (which is room temperature considered as 30 deg. C) the frequency at Mode 1 is obtained as 29.36 by exact solution and 31.23 from experiment, which is amounting to a percentage of error of 7%. At
=0 (which is room temperature considered as 30 deg. C) the frequency at Mode 1 is obtained as 29.36 by exact solution and 31.23 from experiment, which is amounting to a percentage of error of 7%. At 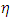 = 1.0 and
= 1.0 and 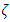 =10 (change in temperature of 30 deg. C), the frequencies obtained for Mode 1 is 19.79 and 21.62 respectively. The experiments were conducted for pressure of up to 3.0 only, due to the discharge pressure limitation of the pump.
=10 (change in temperature of 30 deg. C), the frequencies obtained for Mode 1 is 19.79 and 21.62 respectively. The experiments were conducted for pressure of up to 3.0 only, due to the discharge pressure limitation of the pump.Table 3. Comparison of theoretical and experimental results
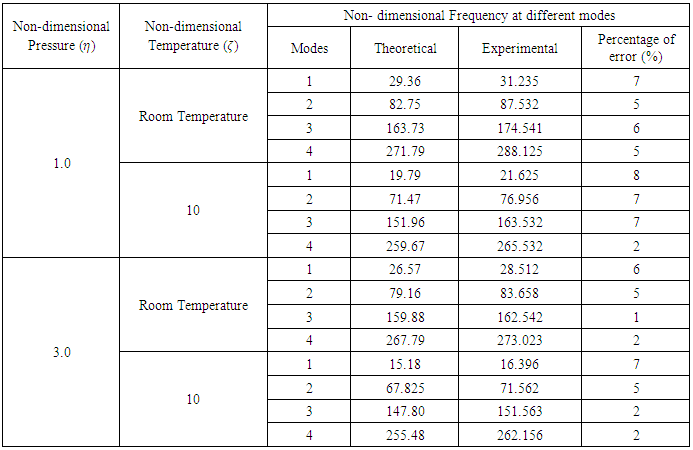 |
| |
|
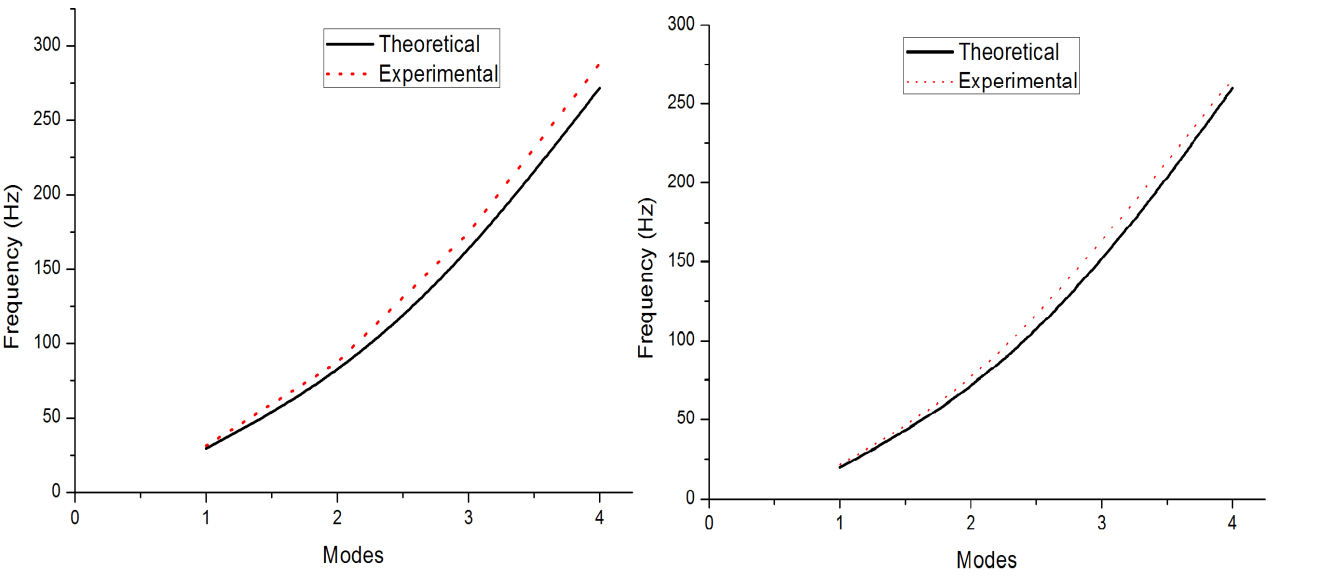 | Figure 9. Comparison of theoretical and experimental frequency at non-dimensional pressure 1.0 unit and room temperature and non-dimensional temperature 10 units |
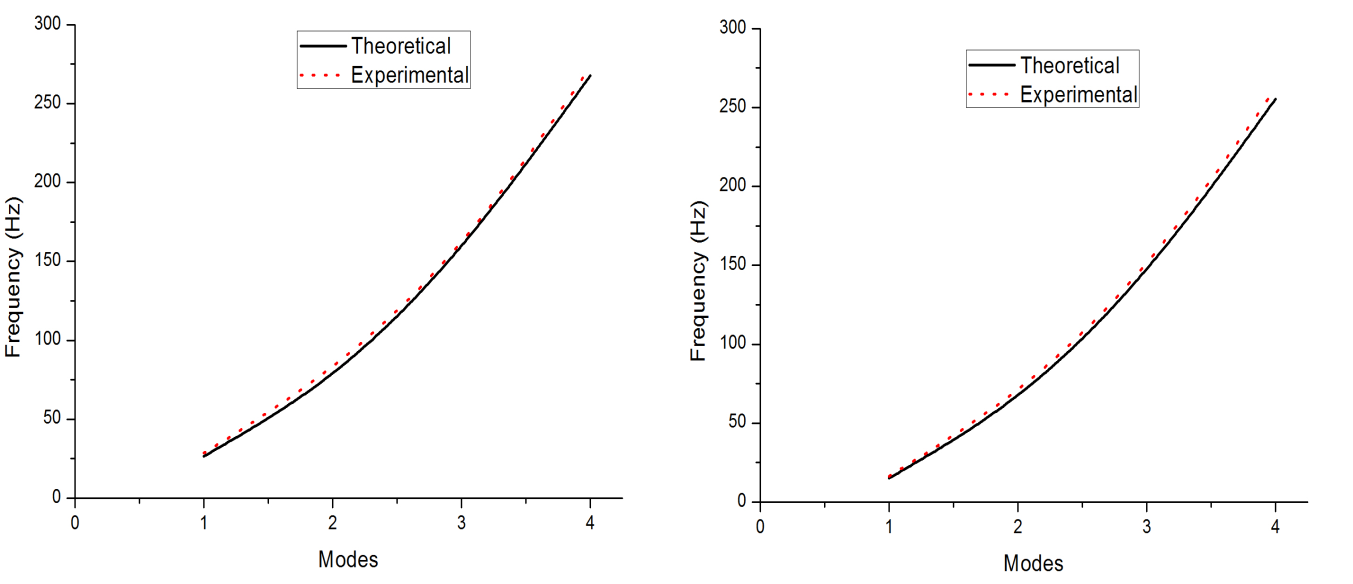 | Figure 10. Comparison of theoretical and experimental frequency of non-dimensional pressure 3.0 unit and room temperature and non-dimensional temperature 10 units |
4. Conclusions
Vibration analysis of a fluid conveying PTFE bellows expansion joint under combined effect of pressure and temperature with fixed ends was studied. Based on the analysis it was observed that the influence of combined effect of pressure and temperature on the fundamental frequency of the fixed PTFE bellows is significant. Results show that the pressure effect on the frequency becomes significant with increase in pressure parameter thereon leads to a decrease in the frequency. The experimental results have confirmed that the transcendental frequency equation derived is exact, within the engineering accuracy of less than 10%.It was studied that any change in temperature for a given pressure rise, will significantly affect the performance of the bellow, and might lead to a failure even before the design conditions are attained.
ACKNOWLEDGEMENTS
The authors wish to thank the Sai Spurthi Institute of Technology-Sathupally, Telangana, India and CSIR-Indian Institute of Chemical Technology-Hyderabad in India for providing the experimental and computational support for the study.
References
| [1] | Anderson. W.F., “Analysis of Stresses in Bellows, Part I Design Criteria and Test Results,” NAA-SR-4527, Atomics International Division of North American Aviation, May 27, 1965. |
| [2] | Anderson. W.F., “Analysis of Stresses in Bellows, Part II Mathematical,” NAA-SR-4527 II, Atomics International Division of North American Aviation, May 27, 1965. |
| [3] | R.C Azar, Chadrashekhar. S and Szaban. P, “On the Computer Aided Axial Vibration Analysis and Design of Metallic Bellows”, 12th Biennial Conference on Mechanical Vibration and Noise, Montreal 17-21 Sept 1989. |
| [4] | EJMA-2008 Standards of Expansion Joint Manufacturers Association, Inc, 9th Edition. |
| [5] | C. Becht IV, “Predicting Bellows Response by Numerical and Theoretical Methods,” Journal of Pressure Vessel Technology, Vol.108, Aug 1986, P334-341. |
| [6] | Bass, R.L., and Holster, J.L., “Bellows Vibration with Internal Cryogenic Flows,” ASME Journal of Engineering for Industry, Vol. 94, 1972, pp. 70-75. |
| [7] | Clark. R.A, “Asymptotic Solutions of Toroidal Shells,” Journal of Applied Mathematics, Vol.16, No.1, Apr 1958. |
| [8] | Rockwell, D., and Naudascher, E., “Review- self-sustaining Oscillations of Flow past Cavities,” ASME Journal of Fluids Engineering, Vol. 100, 1978, pp. 152-165. |
| [9] | Gerlach, C. R. Flow induced vibrations of metal bellows Trans ASME, j. Engg for Industry. 1969; 91: 1196-1202. |
| [10] | Li, Ting-Xin, Guo, B. L. and Li, Tian-Xiang. Natural frequency of U-shaped bellows. Int. J. Pressure Vessels and Piping, 1990; 42: 61-74. |
| [11] | Jakubauskas, V. F. and Weaver, D. S. Natural vibrations of fluid filled bellows, Trans. ASME J. Pressure Vessels Technol., 1996; 118: 484-490. |
| [12] | Jakubauskas, V. F. and Weaver, D. S. Transverse vibrations of bellows expansion joints, Part I: Fluid added mass J. Fluids Structures, 1998; 12: 445-456. |
| [13] | Jakubauskas, V. F. and Weaver, D. S. Transverse vibrations of bellows expansion joints, Part II: Beam Model development and experimental verification J. Fluids Structures, 1998; 12: 457-473. |
| [14] | Broman, G. I., Johnson, A. P. and Hermann, M. P. Determining dynamic characteristics of bellows by manipulated beam finite elements of commercial software. Int. J. Pressure Vessel and Piping, 2000; 77: 445-453. |
| [15] | M. Radhakrishna, C. Kameswara Rao. Axial Vibrations of U-Shaped bellows with elastically restrained end conditions. Int. J. Thin Walled Structures, 2004; 42: 415-426. |
| [16] | M. Radhakrishna, C. Kameswara Rao. Transverse Vibrations of Single Bellows Expansion Joint Restrained against Rotation. Tenth International Conference in Nuclear Engineering, USA, ASME Paper # 22090: 14-17 April, 2000, Arlington, Virginia, USA. |
| [17] | Y. Yan, X.Q. He, L.X. Zhang, C.M. Wang, Dynamic behavior of triple-walled carbon nanotubes conveying fluid. Journal of Sound and Vibration, Elsevier, 319 (2009) 1003-1018. |





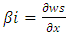 is shear deformation or shear angle in Fig. (3)(a). The fibers are located in an element at a distance as a ‘z from the centerline. The shear deformation has no effect to cause any axial displacement. Hence, the components of displacement can be expressed as
is shear deformation or shear angle in Fig. (3)(a). The fibers are located in an element at a distance as a ‘z from the centerline. The shear deformation has no effect to cause any axial displacement. Hence, the components of displacement can be expressed as 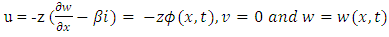

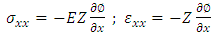
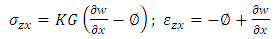
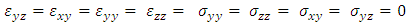
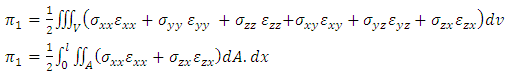
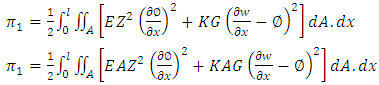
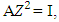 where I is the moment of inertia of the bellow
where I is the moment of inertia of the bellow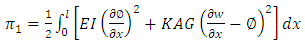
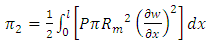
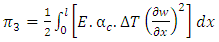
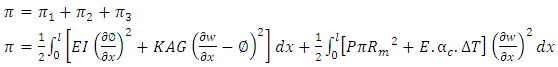
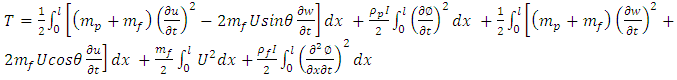
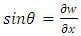
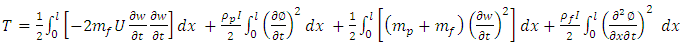
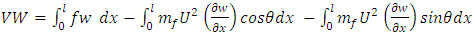
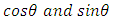
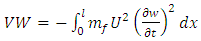
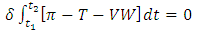
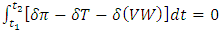
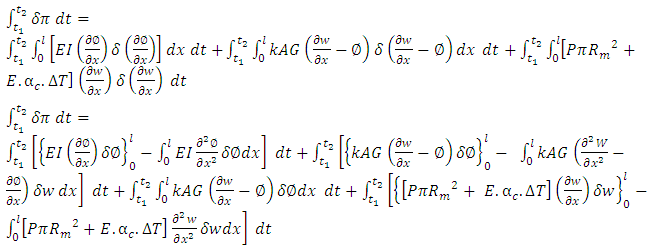
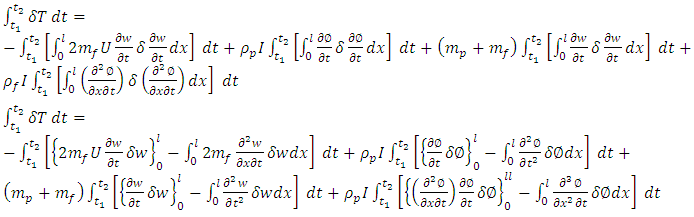
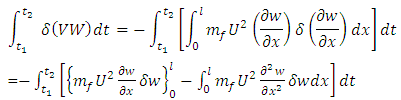
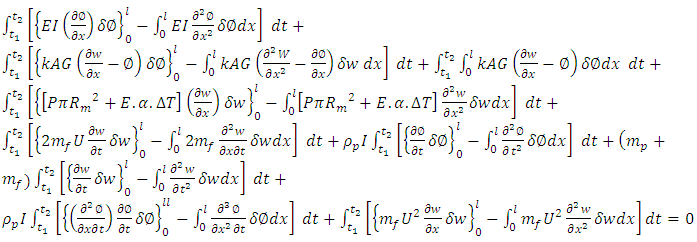
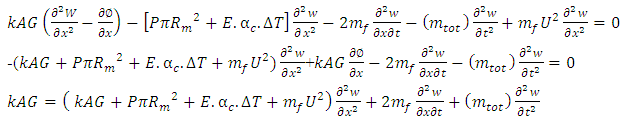
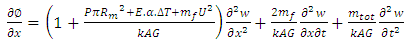
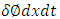
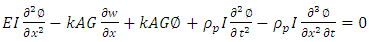
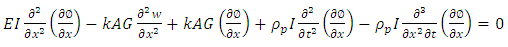
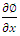 in equation (24), we get
in equation (24), we get 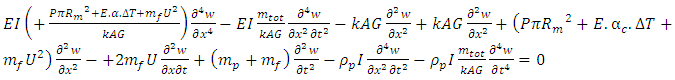
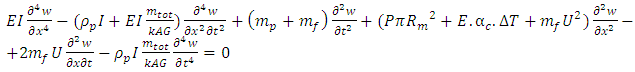
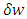
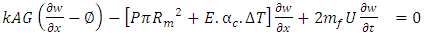
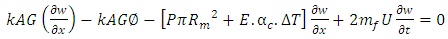
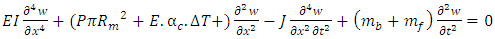
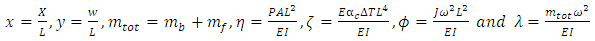
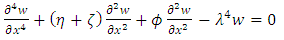
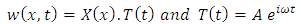
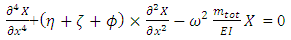
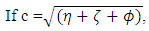
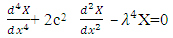
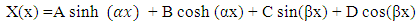
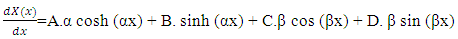
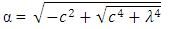
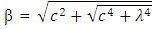
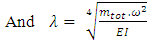
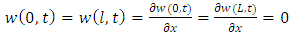
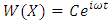
 is circular frequency and C is arbitrary constant.On substitution of Equation. (41) in Equation. (37) the following equation is obtained
is circular frequency and C is arbitrary constant.On substitution of Equation. (41) in Equation. (37) the following equation is obtained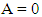
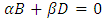
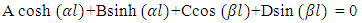
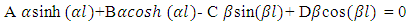
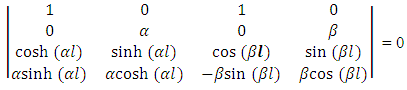
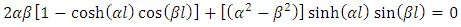

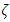 = 18, the fundamental mode frequency is 1.789; whereas, at a pressure of 10 units and
= 18, the fundamental mode frequency is 1.789; whereas, at a pressure of 10 units and 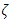 =2, the frequency is 7, which amounts to a decrease of around 74%. It can be inferred that with a change in temperature, there is every likelihood of occurrence of failure of the bellow, for a rise in pressure. This also concludes that the bellow can prematurely fail, even before attaining the required design temperature.
=2, the frequency is 7, which amounts to a decrease of around 74%. It can be inferred that with a change in temperature, there is every likelihood of occurrence of failure of the bellow, for a rise in pressure. This also concludes that the bellow can prematurely fail, even before attaining the required design temperature.
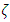 = 38, the frequency obtained is 11.33; at a pressure of 10 units and
= 38, the frequency obtained is 11.33; at a pressure of 10 units and 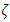 =23, the frequency is 10.768, which amounts to a decrease of around 4%. It is also found that with an increase of pressure term,
=23, the frequency is 10.768, which amounts to a decrease of around 4%. It is also found that with an increase of pressure term, 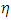 =1 to
=1 to 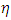 = 3 the temperature term decreases, from
= 3 the temperature term decreases, from 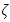 = 39 at
= 39 at 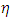 =1 and
=1 and 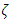 = 36 at
= 36 at 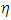 = 3, which is a reduction of 7% in change of frequency.
= 3, which is a reduction of 7% in change of frequency. 


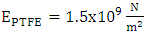 ; Root and crown radius R1 =
; Root and crown radius R1 = 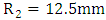 ; Coefficient of thermal expansion
; Coefficient of thermal expansion 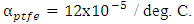 Table 3, figures 9 and 10 represent a comparison and validation of results found by theory and experiments. It is observed that at
Table 3, figures 9 and 10 represent a comparison and validation of results found by theory and experiments. It is observed that at 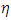 = 1.0 and
= 1.0 and 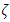 =0 (which is room temperature considered as 30 deg. C) the frequency at Mode 1 is obtained as 29.36 by exact solution and 31.23 from experiment, which is amounting to a percentage of error of 7%. At
=0 (which is room temperature considered as 30 deg. C) the frequency at Mode 1 is obtained as 29.36 by exact solution and 31.23 from experiment, which is amounting to a percentage of error of 7%. At 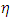 = 1.0 and
= 1.0 and 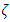 =10 (change in temperature of 30 deg. C), the frequencies obtained for Mode 1 is 19.79 and 21.62 respectively. The experiments were conducted for pressure of up to 3.0 only, due to the discharge pressure limitation of the pump.
=10 (change in temperature of 30 deg. C), the frequencies obtained for Mode 1 is 19.79 and 21.62 respectively. The experiments were conducted for pressure of up to 3.0 only, due to the discharge pressure limitation of the pump.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

