-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2018; 8(1): 7-31
doi:10.5923/j.jmea.20180801.02

Analysis, Correlation, and Estimation for Control of Material Properties
Timothy Sands, Clinton Armani
Defense Advanced Research Projects Agency (DARPA), Arlington, VA, USA
Correspondence to: Timothy Sands, Defense Advanced Research Projects Agency (DARPA), Arlington, VA, USA.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

System identification algorithms use data to obtain mathematical models of systems that fits the data, permitting the model to be used to predict and design controls for system behavior beyond the scope of the data. Thus, accurate modeling and characterization of the system equations are very important features of any mission. These system equations are principally populated with variables from physics (e.g. material properties). Simple control algorithms begin by using the governing physics expressed in mathematical models for control, but usually more advanced techniques are required to mitigate noise, mismodeled system parameters, of unknown/un-modeled effects, in addition to disturbances. Characterization of the physical system a priori is an important step, and this research article will describe research into identifying system equations for several complex structures. Under the auspices of the Digital Manufacturing Analysis, Correlation and Estimation (DMACE) (pronounced “DEE-MACE”) Challenge, the Defense Advanced Research Projects Agency (DARPA) digitally manufactured several complex structures and then conduct a series of structural load tests upon them to determine material properties. Data from the manufacture and load tests was then posted on the worldwide web. Participants were challenged to develop a correlation model that accurately correlates digital manufacturing (DM) machine inputs to output structural test data. Participant models were then evaluated by their ability to predict the test results of the final DM structures. The model that most accurately predicted the final test results won the Challenge. Many disparate technical approaches were investigated by researchers from all over the world, and this paper introduces readers to several of those interesting technical approaches. The authors have permission to publish these government owned submissions, but every efforts is made to credit the researchers themselves, and furthermore each submission is presented in its original form to the maximum extent permitted by the journal’s peer reviewers and editors.
Keywords: Additive digital manufacturing, DARPA, Defense Advanced Research Projects Agency, DMACE Challenge, Digital Manufacturing Analysis, Correlation, and Estimation Challenge, DARPA Challenge
Cite this paper: Timothy Sands, Clinton Armani, Analysis, Correlation, and Estimation for Control of Material Properties, Journal of Mechanical Engineering and Automation, Vol. 8 No. 1, 2018, pp. 7-31. doi: 10.5923/j.jmea.20180801.02.
Article Outline
1. Introduction
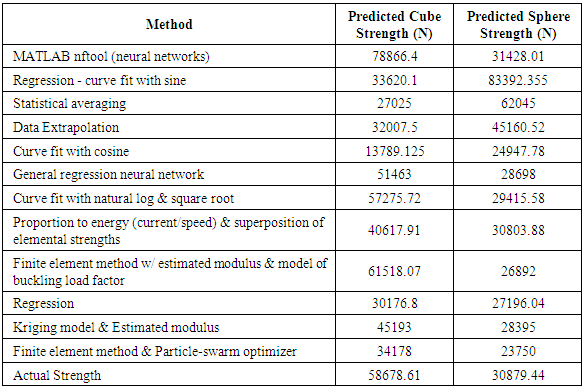
- Space system guidance and control algorithms need a source of systems states to function properly and the most common two sources (usually used in concert together) are state estimators and sensors. Which system model and sensor models should engineers choose? Astrom and Wittenmark described the techniques in their textbook on adaptive control [1]. Slotine [2, 3] reveals adaptive control techniques that utilize system and sensor math models in their adaptive strategies can often make acceptable system identifiers. Fossen [4] subsequently improved Slotine’s technique with mathematical simplifying problem formulation, and Sands [5, 7-11] and Kim [6] developed further improvements to the algorithm based on Fossen’s problem formulation followed by Nakatani [12, 13, 32] and Heidlauf-Cooper [14, 15], but alas these improvements were not revealed in time for publication in Slotine’s text. Troublingly, Wie [16] elaborated singularities that exists in the control actuation that can exacerbate or defeat the control design as articulated [17-21], 0 and solved by Agrawal [22]. Lastly, Sands [23], [24], 0 illustrated ground experimental procedures and on-orbit algorithms for system identification. This research article reveals initial system identification procedures using ground experiments and several data analysis techniques. The aforementioned technical developments individually address key facets that facilitate challenging defense department missions in space 0. Under the Digital Manufacturing Analysis, Correlation and Estimation (DMACE) (pronounced “DEE-MACE”) Challenge, DARPA digitally manufactured several complex structures [25, 26] and then conduct a series of structural load tests upon them. Data from the manufacture and load tests was then posted on the worldwide web. Participants were challenged to develop a correlation model that accurately correlates digital manufacturing (DM) machine inputs to output structural test data. Participant models were then evaluated by their ability to predict the test results of the final DM structures. The model that most accurately predicted the final test results won the Challenge. Many disparate technical approaches were investigated by researchers from all over the world, and this paper introduces readers to several of those interesting technical approaches.
 | Figure 1. Participants in the DARPA DMACE Challenge |
2. Materials and Methods
2.1. Titanium Digital Manufacturing
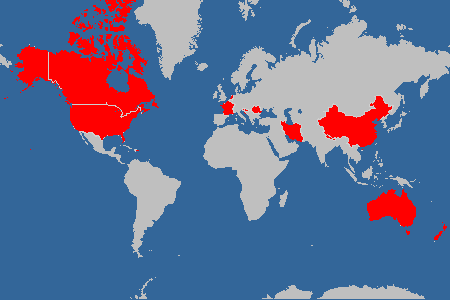
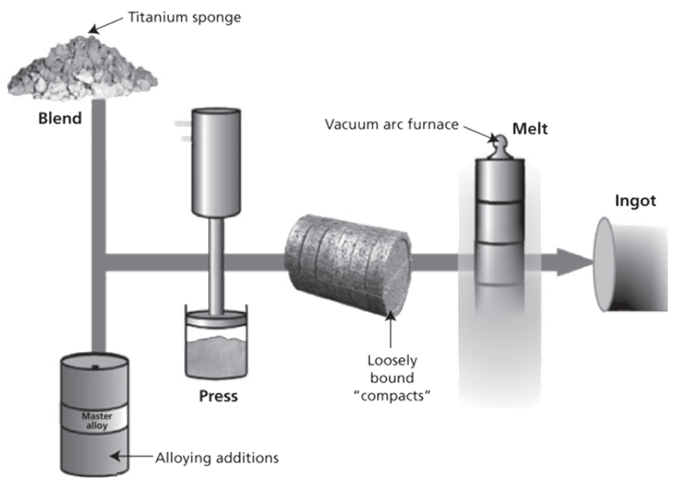
- Manufacturing parts in titanium often proves to be an expensive process displayed in Figure 2 and Figure 3. Notice how many extensive processes are required to modify titanium from an ore (precursor to sponge) to a final part. All of these processes drive the cost of parts made from titanium.
 | Figure 2. Vacuum arc process for converting titanium into ingot [Seong] |
 | Figure 3. Converting titanium ingot into a part [Seong] |
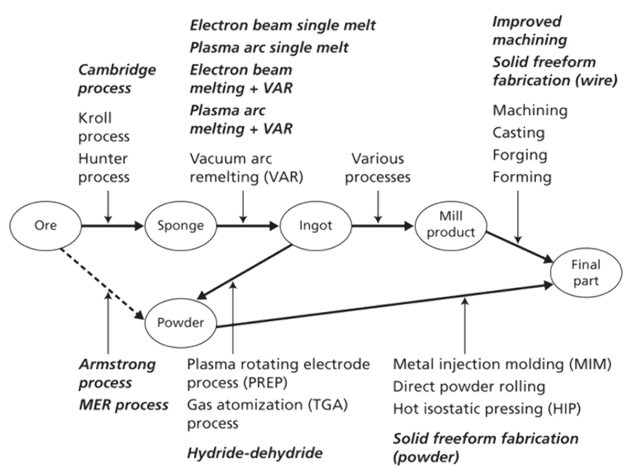 | Figure 4. Emerging technologies for titanium production [Seong] |
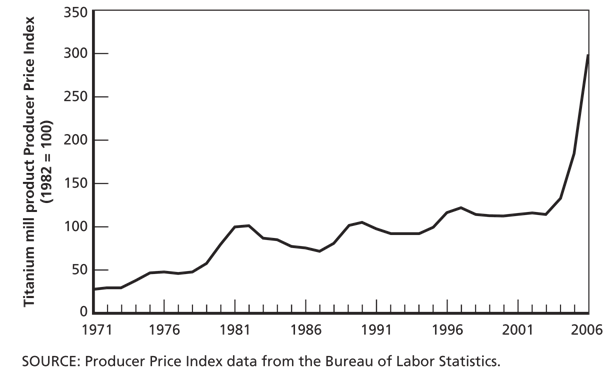 | Figure 5. Titanium mill products producer price index trend [Seong] |
2.2. Titanium Spheres
- Titanium Spheres were digitally manufactured using an Arcam A with an electron beam (e-beam) melting process and Ti6Al4V titanium alloy powder. During the build of the titanium spheres, two input parameters in the e-beam control were varied:1) e-beam velocity (100, 200, and 300 mm/sec),2) e-beam current (1.3, 1.7, and 2.1 mA).The build direction is defined as the vertical axis at which the e-beam machine built the spheres. Furthermore, each sphere had two distinct geometric axes of symmetry, which were structurally different. The two axes of symmetry were recognizable on the sphere surface by a square grid of titanium mesh or a hexagonal grid of titanium mesh along the diameter of the sphere.For the Challenge, the build direction was aligned through the sphere diameter along one set of the square grids. This particular set of square grids was referred to as 0° from build direction. Another set of square grids was located at 90° from the build direction. The hexagonal grids were located at 60° from the build direction. Each sphere was tested in compression to failure along one of these three axes (0°, 60°, 90°) to the build direction. During the compression tests, the maximum (or ultimate) compressive load was recorded. The average maximum load, standard deviation, and maximum load of repeated tests were summarized, along with individual and summary plots, in a single Excel data file. These files are available online at www.dmace.net for registered participants.81 spheres were tested at 0° from the build direction, 81 spheres were tested at 90° from the build direction, and 6 spheres were tested at 60° from the build direction. This equals a total of 168 total spheres as a minimum, for which the data is available to participants for model development.The first 9 Excel files of sphere data posted on the website were crushed at 0° from the build direction, consisting of a full factorial of the 3 beam velocities and 3 current settings with 9 repeats at each condition. This resulted in a total of 81 spheres. The second 9 Excel files of sphere data posted on the website consist of the same 9 combinations of e-beam velocities and current settings, however the spheres were tested at 90° from the build direction. Both the 0° and 90° scenarios are geometrically the same; however, the 90° scenario is perpendicular to the build direction. Additionally, a single set of 6 spheres at a single beam velocity and current were tested at 60° from the build direction.In summary: 81 spheres were tested at 0° from the build direction, 81 spheres were tested at 90° from the build direction, and 6 spheres were tested at 60° from the build direction. This equals a total of 168 total spheres as a minimum, for which the data is available to participants for model development.
 | Figure 6. One-piece titanium mesh spheres directly from powder |
 | Figure 7. Load-test of one-piece titanium mesh spheres |
2.3. Polymer Cubes
- The polymer cube problem is different from the titanium sphere problem in that initial tests were performed to establish basic material properties, and then subsequent tests evaluated structures made from the basic material.The polymer material properties were suspected to be anisotropic and bi‐modular, so the compression and tension tests were conducted in order to establish the basic material properties of the polymer (ABS‐M30 production‐grade thermoplastic) extruded by the 3‐D printer (FORTUS 400mc). During the build of the compression and tension specimens, four processing variables were varied:1) printer tip size (T12=0.178 mm and T16=0.254 mm),2) machine raster angle (0° and 90°),3) machine build angle (0° and 90°), and4) bake time after fabrication (0 and 12 hours), referring to how long the sample remained in the printer‐oven after fabrication.Figure 8 below provides a visual reference for the raster and build angles.
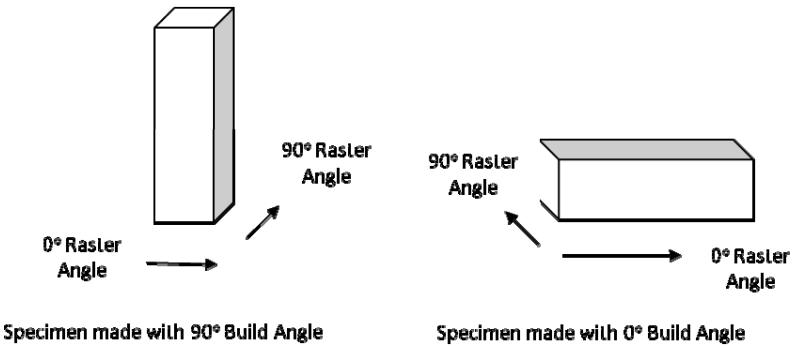 | Figure 8. Nomenclature for digital manufacture of polymer cubes |
 | Figure 9. “Dogbone” samples used to evaluate DM polymer properties |
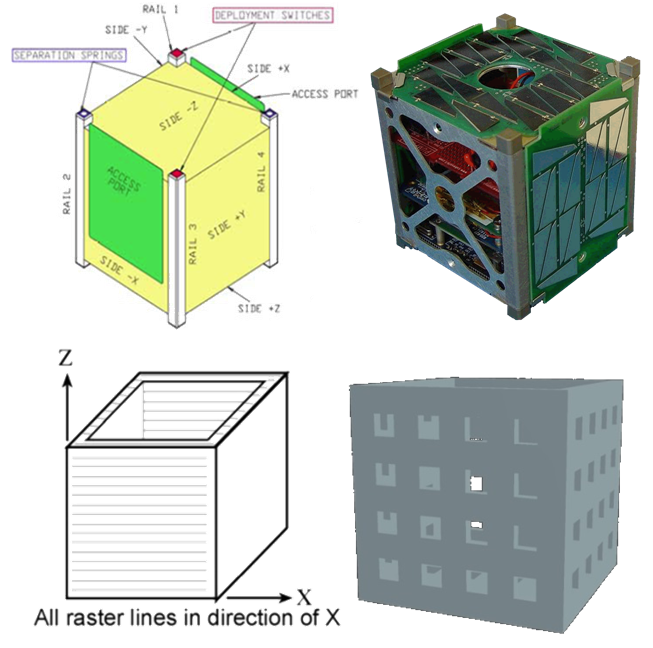 | Figure 10. Sample CubeSat structures |
 | Figure 11. Final contest CubeSat structure being crushed |
2.4. Putting It all Together
- For the DMACE Challenge, participants submitted predictions for the maximum compressive load in newtons for both the final titanium sphere configuration and the final cube configuration. Predictions and model descriptions were submitted by 1630 EST, December 6, 2010. A winner was be determined by DARPA using sample mahalanobis distance, and the winning team or individual received the $50,000 Challenge prize.
3. Results – Individual DARPA Challenge Submissions
- In the paragraphs that follow, individual submissions are inserted from the original source authors listed in the acknowledgements. Only minor edits for grammar and format into this paper were made on the original submissions of the authors. All submissions to DARPA are not included in this paper, rather a sampling of several different techniques and variations of the same technique are presented here. The submissions are listed by official affiliation, while authors and participants are listed in the acknowledgements.
3.1. Submission 1: University of Missouri-Columbia
- The models used for predicting maximum load for both the sphere and the cube were accomplished using neural networks. Utilizing the nftool command in Matlab, a network for each was trained using the test data to provide sample inputs and targets. Note that the inputs and targets were normalized about the maximum values for each parameter to improve network performance. The networks were then simulated under the test conditions to predict the maximum loads for both example cases. The inputs given to the sphere network included current, velocity, and crush angle. The inputs for the cube network were tip size, raster angle, build orientation, and hours “baked.” An additional term for the aspect ratio of the loaded surface was included to make the network adaptable to various geometries. The outputs from both networks then are values between 0 and 1, which are multiplied by the respective maximum loads from each dataset to determine the final maximum load for the given case. Predicted strength for the cube is
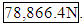 Predicted strength for the sphere is
Predicted strength for the sphere is 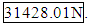
3.2. Submission 2: Greystones Group
- I went with a numerical analysis approach. After seeing the test data provided up to the 2nd practice question was approximately unimodal, I decided to try symbolic regression software. After seeing the data for the 3rd and final estimations it became clear that CAD or FEA software might provide better modeling for the cube. After looking at all the data and calculating the surface area of the spiral cube, I just guessed at a scaling value of the 2nd practice cube average max force. So I guess that however my brain signals were configured over the time I was looking at the data is the implicit math model for the final cube data estimate.Math model for spheres, where force p [Newtons] is a function of current c [mA], velocity v [mm/sec] and crush angle a [degrees] (this was used for the final question estimation):
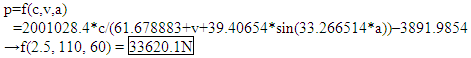 Math model for cubes, for the final question estimation:
Math model for cubes, for the final question estimation: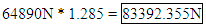 Math model for cubes, for the 2nd practice question estimation, a area, t tip size, r raster angle, b build angle:p = g(t,r,b,a) = a*(59.430218+38.952698*t + 7.5636129*cos(0.372657+b-0.052924275*r) / (41.201572*t*t - 0.60272503))
Math model for cubes, for the 2nd practice question estimation, a area, t tip size, r raster angle, b build angle:p = g(t,r,b,a) = a*(59.430218+38.952698*t + 7.5636129*cos(0.372657+b-0.052924275*r) / (41.201572*t*t - 0.60272503))3.3. Submission 3: Pennsylvania State University
3.3.1. Sphere Model
- The sphere model uses the average maximum load values for the calculation average maximum force of desired conditions. First step-The standard deviation of average maximum load for currents 1.3 mA, 1.7 mA and 2.1 mA for 0 degrees of crush angle have been calculated. This calculations covers all velocity ranges (100-300 mm/sec) for corresponding current value and crushing angle. This process has been repeated for 90 degrees of crush angle. See Figure 12. Second Step- Then these calculated standard deviation values are further divided by the square of the velocity displacement of the data they have been comprised from. This would be (300-100=200). The calculated values are represented in blue boxes in the figure. Third Step-Average of all these values obtained in second step (which is calculated as 0.15076) is used to determine the standard deviation of the average maximum load for the desired conditions. This is obtained by multiplication of the average obtained value by the square of the velocity displacement for the desired conditions (135-110=25). The multiplication is due to the pattern of increase in in maximum load whenever there is a decreased velocity condition. Last Step-Having the given data and calculating the standard deviation for the average maximum load enables us to use the solver application to reach to the desired result of average maximum load of
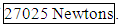
 | Figure 12. Calculations of Sphere Model |
3.3.2. Cube Model
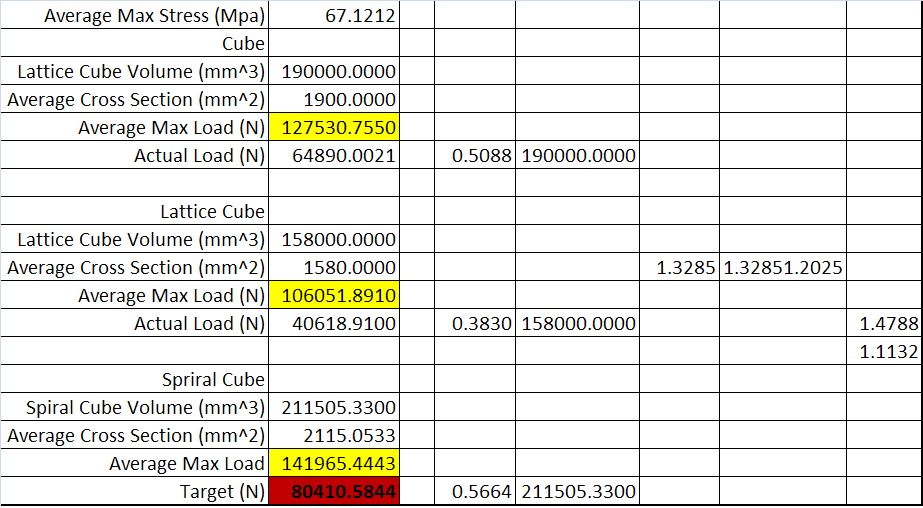
- The first step in cube model deals with calculating the area under compression first for a cube with no windows. Then estimated maximum stress is calculated by using the average maximum stress values. The ratio between actual load and average maximum load is calculated. (can be seen as fraction in the Figure 13) Same calculations are also carried out for the lattice cube (cube with windows) and the ratio between actual load and average maximum load is calculated. The average of these two ratios (fractions) has been calculated. After calculating spiral cube compression area and average maximum load respectively. The fraction value obtained from two previous cube calculations is used to determine the actual load for spiral cube. The final answer has been calculated as:
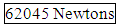
 | Figure 13. Calculations of Cube Model |
3.4. Submission 4: “Snowballs Chance”
3.4.1. Titanium Sphere Predictions
- The goal of the titanium sphere predictions was to estimate the maximum compressive load that a sphere made with a current of 2.5 mA, velocity of 110 mm/s, and a crushed at an angle of 60 degrees could sustain. There is no given data for a velocity of 110 mm/s, but there is data for velocities at 100, 200, and 300 at angles of 0 and 90 degrees with currents of 1.3, 1.7, and 2.1 mA. There is also data for current at 2.5 mA and 135 mm/s and an angle of 60 degrees. The first step taken in the modeling process was to predict what the curve for a variation with speed chart would look like. This was accomplished by using Figure 14 and extrapolating to determine how much the maximum load varies with current. The right set of data points in Figure 14 are the estimated data points.
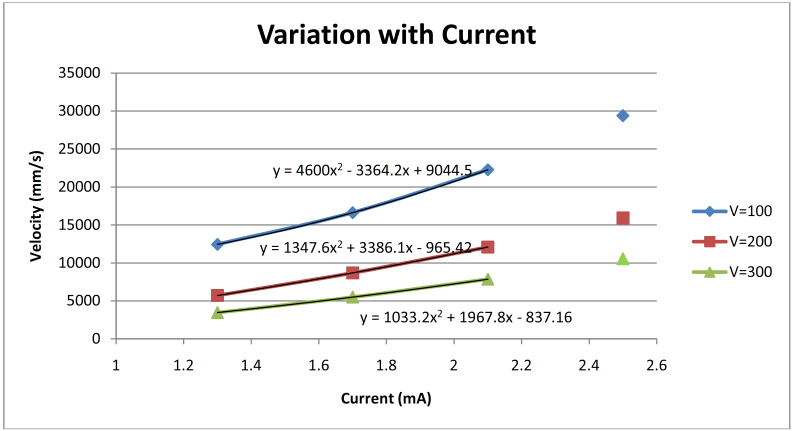 | Figure 14. Sphere data extrapolation |
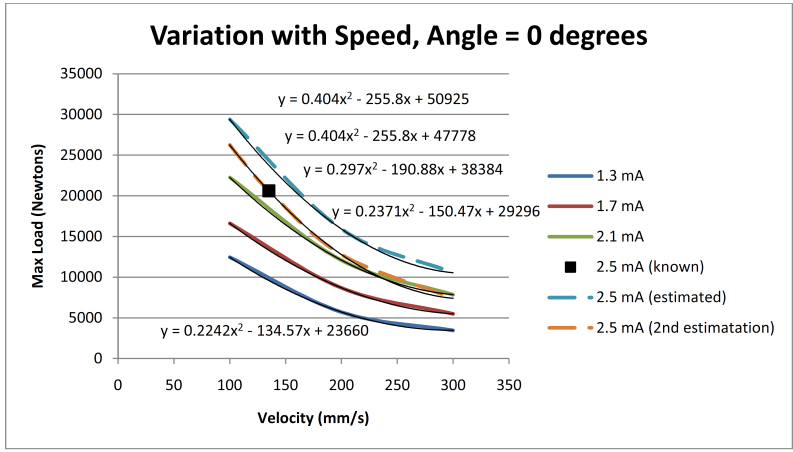 | Figure 15. Sphere data extrapolation |
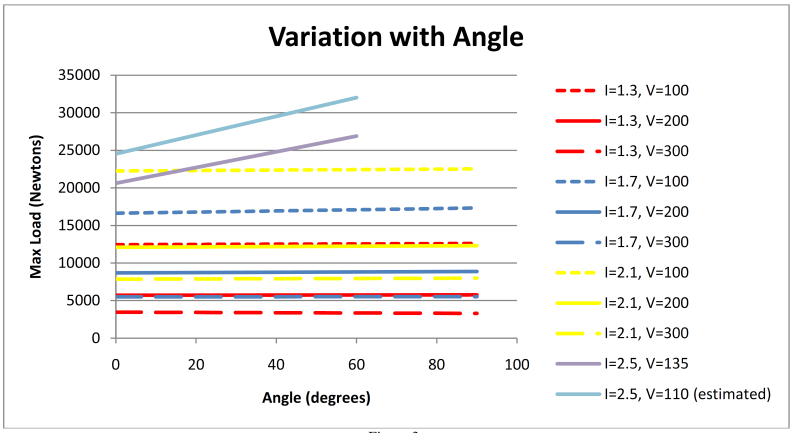 | Figure 16. Sphere data extrapolation |
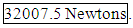
3.4.2. Cubic Predictions
- The goal for the cubic predictions was to model the maximum load that a digitally manufactured cube could withstand. In order to accomplish this, the maximum load on a cube with solid outer walls was known, as well as the maximum load for a cube with lattice outer walls. The unknown was a cube built as in Figure 17.
 | Figure 17. Unknown Cube configuration |
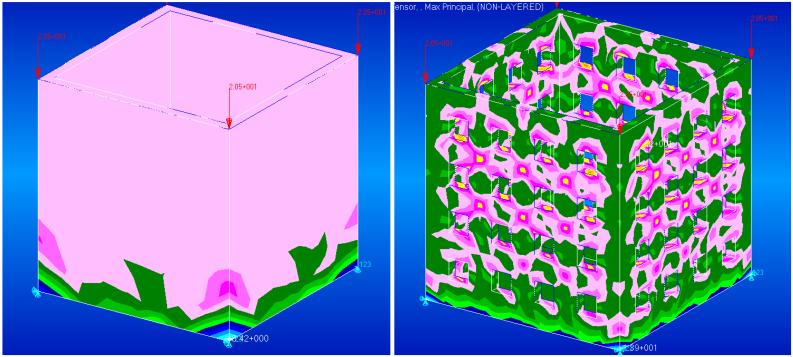 | Figure 18. Known cube configurations |
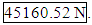
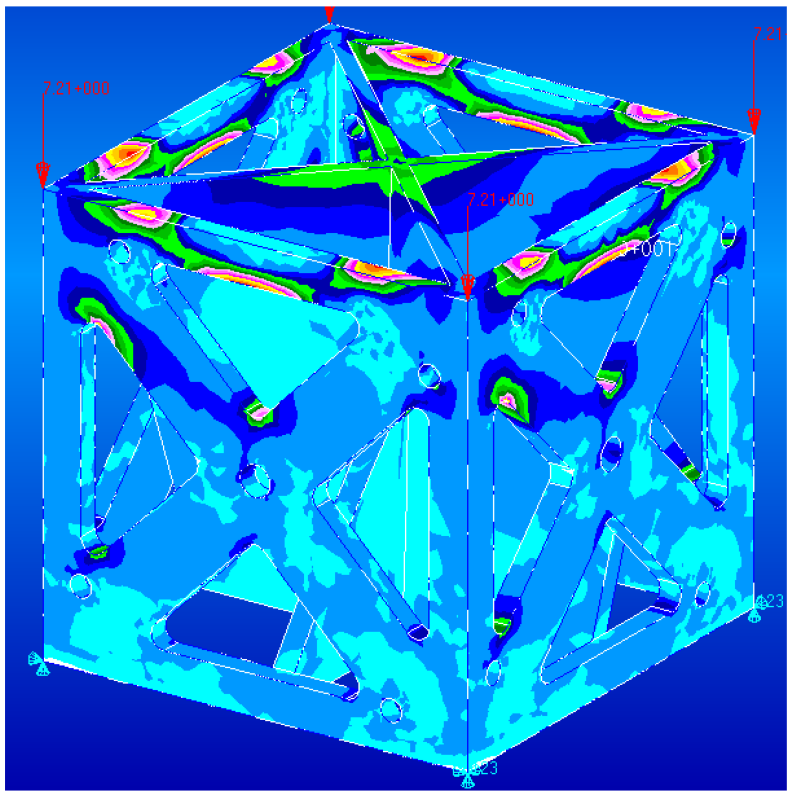 | Figure 19. Final test specimen |
3.5. Submission 5: Embry-Riddle & Harvard Cavanaughs
- The DARPA DMACE Challenge seeks to determine if it is possible to predict the strength of a structure constructed via rapid prototyping methods. This contest will select the participant group with the closest estimation to two test samples as a winner, provided that documentation of the method used in the estimation is provided. This document describes the method used by “Team Cavanaugh" in fulfillment of that requirement.
3.5.1. Sphere Challenge
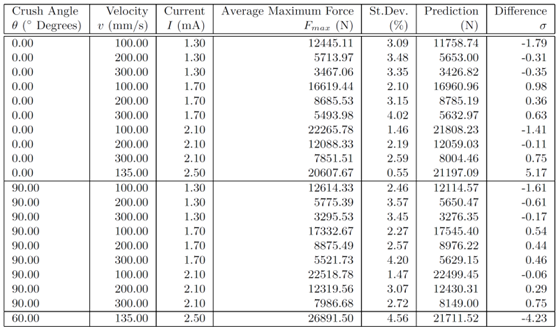
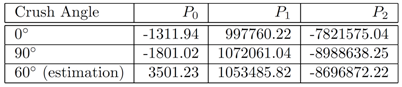
- The sphere challenge tested a complicated spherical shape with 6-fold symmetry made of a titanium alloy with the Arcam A2 additive manufacturing device. This device uses an electron beam to melt a titanium alloy powder, thus fusing together neighboring pieces of the powder into a solid structure. The input parameters to the machine included the speed at which the beam was moved across the material, v, and the current of the electron beam, I. Spheres created by this system were then tested for strength by crushing the sphere at in a direction relative to the build angle, (either 0° or 90°). For each combination of input parameters and crush angle, a sample of ten different spheres was generated and tested. The Model: The goal of this model is to be able to predict the strength of an sphere created with an arbitrary set of input parameters and crush angles. Here, the strength of a sphere is defined as the average maximum amount of force, Fmax, that a sphere can withstand before complete failure. A decision was made to separate the data based on crush angle in the event that there was some angular dependency. A prediction for an arbitrary angle and input parameters, P(v,I,θ) would then be calculated by combining the prediction for the tested angles according to the following way:
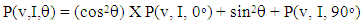 | (1) |
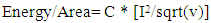 | (2) |
|
|
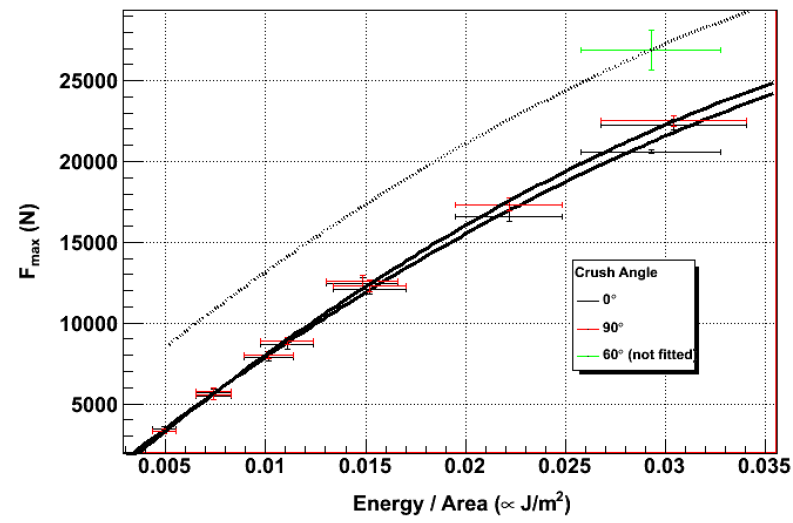 | Figure 20. Maximum force sustained versus energy/area |
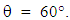 The prediction for this set of parameters is
The prediction for this set of parameters is 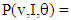
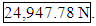 Sphere SummaryWhile this statistical method provides a means to predict the strength of this unique spherical structure, this exercise does not actually examine the resulting properties of the material formed. A more thorough test would have generated bar samples for material strength tests, as done in the other part of the challenge. Very little is known about the underlying structure of the material. It would have been instructive to have samples crusted at 45°.[1] 3.5.2 Prototype Method 2 - ThermoplasticThe second challenge tested a different manufacturing technique which involved creating various sample geometries, and cube-structures in a FORTUS 400mc thermoplastic 3-d printer with ABS-M30 thermoplastic. The manufacturing process involves a variable width nozzle that extrudes the thermoplastic material in layers. The final geometry to be tested was one roughly the size of a cube- satellite. Cube satellites are purpose built for a multitude of missions but they share the same external dimensions. Having an ability to build and predict performance of various structural designs would be highly desirable. Compression and tensile tests were performed on the thermoplastic samples to demonstrate the material properties of the various manufacturing orientations. Each set of samples differed by extrusion diameter, raster angle (the direction at which the nozzle moved while extruding the thermoplastic in the oven), and by build angle (the direction between the longitudinal axis of the part and the oven floor). Half of the samples were heat cured for 12 hours prior to test. Three cube structures were then produced with various open and closed wall designs, similar to many weight saving techniques used in aerospace structures. The first two were sample designs and the third was the challenge test subject. 2.1 The Model This method of manufacturing seems to have much higher repeatability as compared to the Arcam A2 machine. The test structure is a five sided box with solid sides. This structure can withstand 64890 ± 779.8867 N before failure. The contest asks us to predict a structure that has cutouts. The solid wall box can be estimated as being comprised of many adjacent columns. When the cutouts are made, the number of effective columns is reduced.In the test cutout box, the effective column count is reduced by 40% when four columns of 10 mm cutouts are made per side in the 100 mm per side box, the resulting strength should be reduced by 40%. This thinking leads to a prediction for this test structure of a maximum force of 38934 ± 467.93 N which is well within the agreement of the actual value which is 40616.91 ± 885.19 N. Note that the estimation is off by only -1.9.The Challenge ProblemThe challenge problem provides for a more complicated problem that the simple cutout challenge problem. The structure now has no bottom, has substantial cutouts of the four sides (with cross members) and has an inner spiral which serves to give a non uniform support to the walls. This structure is substantially different from the other two structures because it does not have any bottom. As such, it can be roughly modeled as four corner columns held in a configuration by the cross members. The box is loosely prevented from caving in by the spiral structure, although it is not simple to perform this calculation without advanced simulation software. The estimation therefore will seek to pull the entire strength of the structure from the four corner beams. Each corner beam is approximately 10mm on each side and 5mm thick. This Following the adjacent column model described previously, this would result in a total of 80mm of 5mm thick columns for the wall of the structure. The center of the spiral provides an additional 5mm by 5mm column, for a total of 85mm of effective 5mm column. The test box had effectively 400mm of 5mm column. Therefore, neglecting the absence of a bottom, this final challenge box should capable of support a force of 85mm/400mm X 64890.00N =
Sphere SummaryWhile this statistical method provides a means to predict the strength of this unique spherical structure, this exercise does not actually examine the resulting properties of the material formed. A more thorough test would have generated bar samples for material strength tests, as done in the other part of the challenge. Very little is known about the underlying structure of the material. It would have been instructive to have samples crusted at 45°.[1] 3.5.2 Prototype Method 2 - ThermoplasticThe second challenge tested a different manufacturing technique which involved creating various sample geometries, and cube-structures in a FORTUS 400mc thermoplastic 3-d printer with ABS-M30 thermoplastic. The manufacturing process involves a variable width nozzle that extrudes the thermoplastic material in layers. The final geometry to be tested was one roughly the size of a cube- satellite. Cube satellites are purpose built for a multitude of missions but they share the same external dimensions. Having an ability to build and predict performance of various structural designs would be highly desirable. Compression and tensile tests were performed on the thermoplastic samples to demonstrate the material properties of the various manufacturing orientations. Each set of samples differed by extrusion diameter, raster angle (the direction at which the nozzle moved while extruding the thermoplastic in the oven), and by build angle (the direction between the longitudinal axis of the part and the oven floor). Half of the samples were heat cured for 12 hours prior to test. Three cube structures were then produced with various open and closed wall designs, similar to many weight saving techniques used in aerospace structures. The first two were sample designs and the third was the challenge test subject. 2.1 The Model This method of manufacturing seems to have much higher repeatability as compared to the Arcam A2 machine. The test structure is a five sided box with solid sides. This structure can withstand 64890 ± 779.8867 N before failure. The contest asks us to predict a structure that has cutouts. The solid wall box can be estimated as being comprised of many adjacent columns. When the cutouts are made, the number of effective columns is reduced.In the test cutout box, the effective column count is reduced by 40% when four columns of 10 mm cutouts are made per side in the 100 mm per side box, the resulting strength should be reduced by 40%. This thinking leads to a prediction for this test structure of a maximum force of 38934 ± 467.93 N which is well within the agreement of the actual value which is 40616.91 ± 885.19 N. Note that the estimation is off by only -1.9.The Challenge ProblemThe challenge problem provides for a more complicated problem that the simple cutout challenge problem. The structure now has no bottom, has substantial cutouts of the four sides (with cross members) and has an inner spiral which serves to give a non uniform support to the walls. This structure is substantially different from the other two structures because it does not have any bottom. As such, it can be roughly modeled as four corner columns held in a configuration by the cross members. The box is loosely prevented from caving in by the spiral structure, although it is not simple to perform this calculation without advanced simulation software. The estimation therefore will seek to pull the entire strength of the structure from the four corner beams. Each corner beam is approximately 10mm on each side and 5mm thick. This Following the adjacent column model described previously, this would result in a total of 80mm of 5mm thick columns for the wall of the structure. The center of the spiral provides an additional 5mm by 5mm column, for a total of 85mm of effective 5mm column. The test box had effectively 400mm of 5mm column. Therefore, neglecting the absence of a bottom, this final challenge box should capable of support a force of 85mm/400mm X 64890.00N = 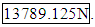 This estimation does not account for the fact that the structure is more likely to fail after rotating about Z, whereas the original test box did not express a rotational preference as a failure mode.Thermoplastic SummaryThis statistical method relied on more consistent sample sets; however each sample set only contained only two data points. Additional repetitions of each sample set would have improved the robustness of the model. More complex cube-sat geometries would require different lab tests to be conducted to test the shear-interface between multiple layers of thermoplastic.
This estimation does not account for the fact that the structure is more likely to fail after rotating about Z, whereas the original test box did not express a rotational preference as a failure mode.Thermoplastic SummaryThis statistical method relied on more consistent sample sets; however each sample set only contained only two data points. Additional repetitions of each sample set would have improved the robustness of the model. More complex cube-sat geometries would require different lab tests to be conducted to test the shear-interface between multiple layers of thermoplastic.3.6. Submission 6: North Carolina State A&T University
- A general regression neural network (GRNN) was used to model both the sphere and the cube problems. Data from the previous practice problem was utilized as past history to develop the models. The GRNN is a statistical technique that estimates the most probable curve to fit a collection of points by optimizing the choice of a set of model parameters. It consists of four layers: 1. Input Buffer 2. Gaussian Displacement Layer 3. Summation/Divison Layer 4. Output Layer The input buffer distributes the activity patterns of the input to the neurons in the Gaussian displacement layer. The computation of the Gaussian displacement layer is governed by the following equations.
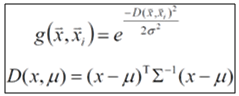 | (3) |
 | (4) |
|
3.6.1. Cube Problem Data Set
- The cube problem data set was formed only from the data given for the compressive load of the previous cubes and only cubes with a 0 degree raster angle. The features in the data set consisted of the type of tip size used, volume of material that made up the cube, and the estimated percentage of material missing from the with respect to its overall volume. To get the fill percentage we estimated the volumes of the cutouts within the box such as the inner triangles in the final block. Max Stress served as the output for the model. (Example below)Final Cube Parameters Used Tip Size: 1 Volume: 205250 mm Fill Pct: 0.20520 Predicted strength is
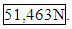
3.6.2. Sphere Problem Data Set
- The sphere problem data set was formed from all of the past data given in the practice problems. The features in the data set consisted of the velocity, current, and crush angle. (Example below)
|
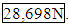
3.7. Submission 7: Auburn University
3.7.1. Modeling of Maximum Compressive Loads for Titanium Spheres
- Machine: Arcam A2 (electron beam melting process) Parameters v = e-beam velocity (100, 200, and 300 mm/sec), I = e-beam current (1.3, 1.7, and 2.1 mA). E = e-beam energy Material: Ti6Al4V titanium alloy powder, Tensile Strength [Titanium Information Group]: min 897 MPa, typical 1000 MPa Tensile Strength [Arcam data sheet]: req, 860 Mpa, 930 Mpa, typical 1020 Mpa. Elastic Modulus [Titanium Information Group]: 114 GPa, Modulus of Elasticity [Arcam data sheet]: 120 Gpa.Angle between build direction and compression testing direction: a (0, 60, and 90 degrees). Sphere Dimensions: The outer diameter is approximately 40mm and inner diameter is approximately 30mm. ModelWe denote by F the maximum compressive load. After analyzing the data, we have the following relations between the involved parameters. Provided that the angle between build direction and compression testing direction is fixed, E-beam velocity (v) is proportional to ln F and also e-beam current (I) is proportional to ln F. So, we have a plane as the surface of the function which gives ln F in function of v and I:
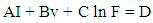 | (5) |
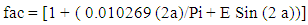 | (6) |
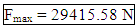
3.7.2. Modeling of Maximum Compressive Loads for Polymer Cubes
- Machine: FORTUS 400mc (3D printer) Parameters • Printer tip size (T12=0.178 mm and T16=0.254 mm) • Machine raster angle: R (0° and 90°) • Machine build angle: B (0° and 90°) • Bake time after fabrication: tc (0 and 12 hours) Material: ABS-M30 production-grade thermoplastic [ABS-M30] Tensile Strength: 36 MPa Tensile Modulus: 2413 MPa Flexural Strength: 61 MPa Flexural Modulus: 2317 Mpa. Compression test specimen geometry: square prism of nominal dimension of 12.7 mm x 12.7 mm x 50.8 mm. MODEL We denote by F the maximum compressive load. According to the experimental data for maximum stress, the build angle and raster angle affect it as follows: It is ordered from higher to lower R0B0, R90B0, R0B90, and R90B90. Smaller print tip size gives higher maximum stress only for the case R0B0. For testing failure we have two options: 1) Compression failure (depends only on critical cross-section area) and 2) Buckling failure (depends directly on the Inertia of the critical cross-section area) by Euler buckling equation. Since the manufacturing process is process is by printing (depositing material), the arrangement of material is layer by layer of a given thickness and the adhesion of one layer against the neighbor layers is the most relevant. So, we will correlate the maximum compressive load with both the smallest critical cross section area (A1) and the lowest Inertia (Ix and Iy) of a critical cross-section area A2.
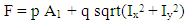 | (7) |
3.8. Submission 8: Isakson Engineering
3.8.1. The Sphere
- The first realization that occurred to me was that the strength of the material is likely a function of the energy put into a given point of the sphere. The rational for this is that the material with more energy put into it will melt together better. So the higher the beam current and the slower the scan, the more energy added and the stronger the material. So I reorganized the data to show the yield strength verses the quantity current/speed. Additionally, however, I expected some leveling off of the strength at higher energy levels as the material will at some point reach the ultimate strength of the raw material completely melted together. I therefore tried to match the data to a sigmoid curve. However, no set of parameters for this seemed to be a good fit. My conclusion is that we are still some distance from the ultimate yield strength (and possibly a sharper inflection then a sigmoid is needed). More tests would have to be performed to determine what the ultimate strength while maintaining good manufacturing tolerances. I therefore fitted the data to a straight line and found a reasonable fit. In Figure 21, you can see the results of this plot. As part of this plot you can see separate trend lines for both the 0 degree crush angle and the 90 degree crush angle. It can be seen that the results indicate slightly higher crush strength at 90 degrees, particularly at higher input energy levels. As will be seen later, this difference is small compared to another problem with the data. This plot also suggests a small change at higher current levels as well. The plot suggests that the higher currents cause a higher strength in the mid energy levels which might decline again at higher levels. This would require the fitting of a curve to fit this, but I do not believe there is sufficient statistics to justify this. Also, a straight line could be fit to just the 2.1 ma (or 2.1 ma and 2.5 ma), 0 degree data (it would change little if the 90 degree data was included as well). However, such fitting would only change the final result a little bit.
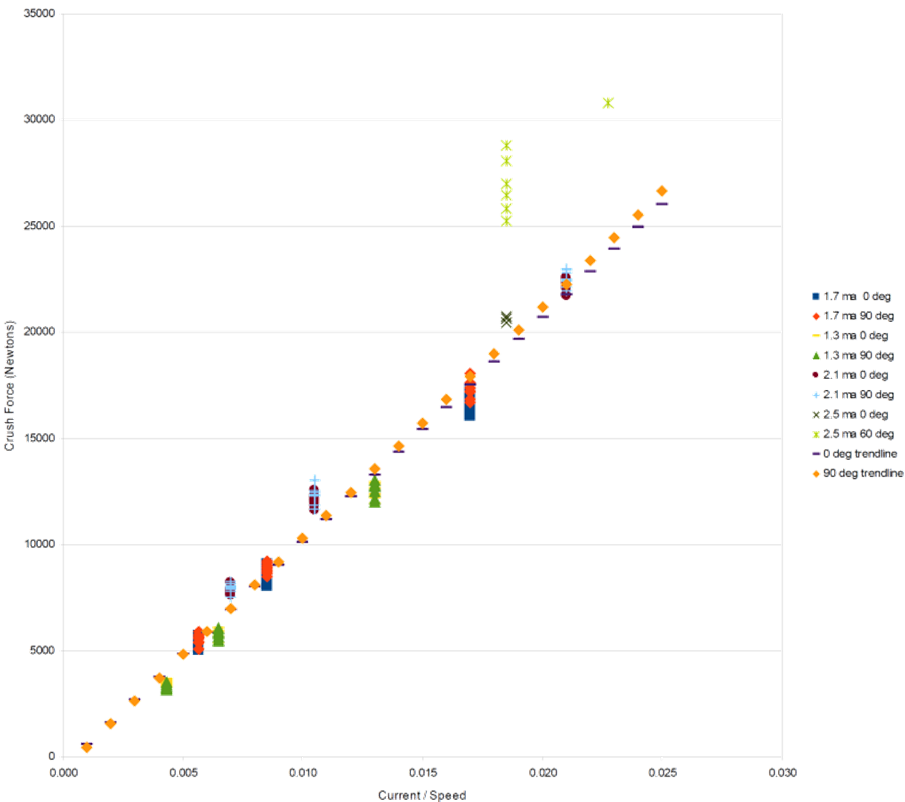 | Figure 21. Data fit to straight line |
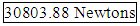 (which I consider the best estimate with the available data). The previous explanations could certainly justify increasing or decreasing the result a little bit, but these errors are minor compared to the last step of the procedure outlined.While the standard deviation (SD) at low energy levels tended to be in the 4% range, as the data moved to higher energy levels the SD fell to around 1.5%. The regression line would have been even better. The limited 2.5 ma 0 degree data was less than 0.4%. However, when the 60 degree data was presented, the SD rose to 5%. I would have thought this was manufacturing out of control, except the 0 degree data came from the same batch and it was highly controlled. As a consequence, this large standard deviation is the largest source of error (by far) in the final result. I would look for a different method of generating this final step, but the data at 60 degrees is very limited and this appears to be the best procedure available.While I do not know what is causing this large SD in the 60 degree crushing tests, I would expect this same problem to exist in the final spheres as well which will give a lower sample Mahalanobis distance.
(which I consider the best estimate with the available data). The previous explanations could certainly justify increasing or decreasing the result a little bit, but these errors are minor compared to the last step of the procedure outlined.While the standard deviation (SD) at low energy levels tended to be in the 4% range, as the data moved to higher energy levels the SD fell to around 1.5%. The regression line would have been even better. The limited 2.5 ma 0 degree data was less than 0.4%. However, when the 60 degree data was presented, the SD rose to 5%. I would have thought this was manufacturing out of control, except the 0 degree data came from the same batch and it was highly controlled. As a consequence, this large standard deviation is the largest source of error (by far) in the final result. I would look for a different method of generating this final step, but the data at 60 degrees is very limited and this appears to be the best procedure available.While I do not know what is causing this large SD in the 60 degree crushing tests, I would expect this same problem to exist in the final spheres as well which will give a lower sample Mahalanobis distance.3.8.2. The Cube
- To determine the crushing force for the cubes, I split the cube into three parts and two types of faces (a total of 6 areas to determine). The three parts are the corners, the X portion on the face, and the spiral. The two faces are the face parallel to the raster scan and the face perpendicular to the raster scan (it is a little more complicated for the spiral, but the idea is the same). For each case, there is two of each part, so the force is multiplied by two. To start with, I should say that while I have some models of how the failures should be occurring, I have found that much of the data does not agree with my (mental) models. As I consequence, I must yield to the data and much of my conclusions as to the final force is based on the data tests result more than what I think should have (but obviously did not) happened. So if my explanations seem to leave a little to be desired, my apologies. I will tell you how I calculated the results I provide. One of the first assumptions that I am making is about the (mounting) holes in the sides of the cubes. They are all located in areas that have a significant polymer around them. As a consequence, I do not believe they will lead to a failure and therefore I am ignoring them. However, confirmation of this would be one advantage to finite element analysis, which I did not do.The Corners
 | Figure 22. The corners |
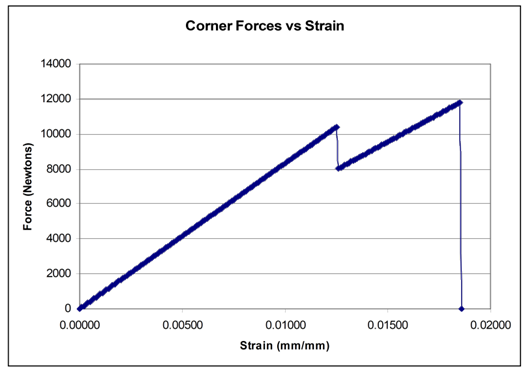 | Figure 23. The corners |
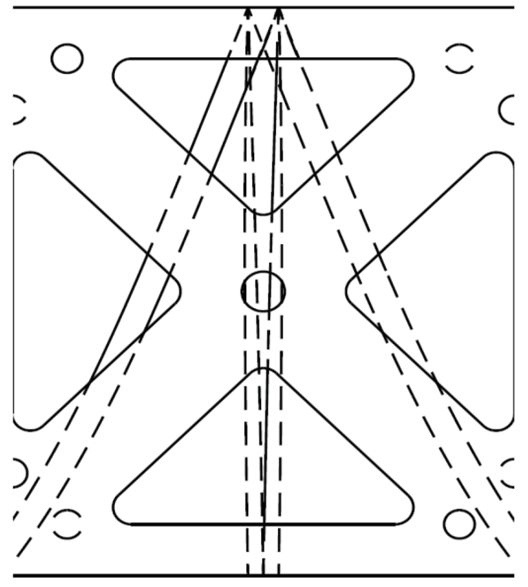 | Figure 24. The X-portion |
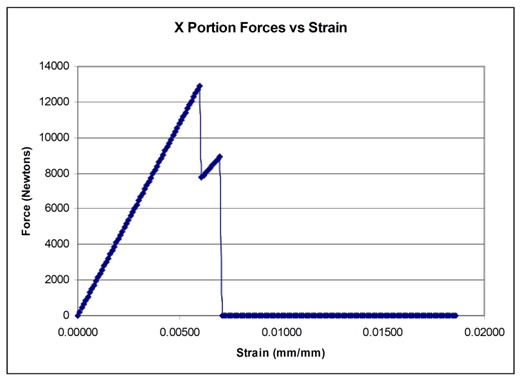 | Figure 25. The X-portion |
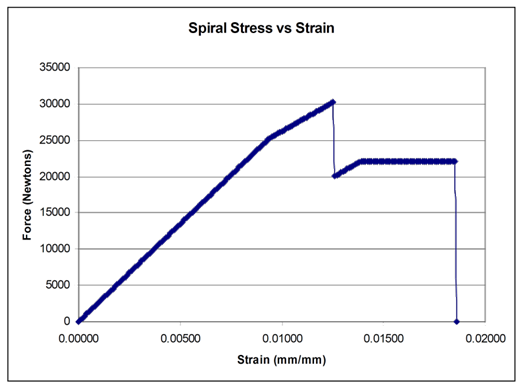 | Figure 26. The spiral |
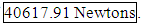
 | Figure 27. The final result |
3.9. Submission 9: University of California, Santa Barbara
3.9.1. Sphere Crushing Model
- The prediction of the sphere crushing load was obtained principally from finite element calculations. To this end, a script was used to generate a model of 1/8th of the sphere, starting from a single unit cell of the lattice structure. The strut length was taken to be 1.08 mm and the inner and outer sphere radii were 30 and 40 mm, respectively. Several different values of strut diameter were used. The mechanical response of the Ti6Al4V alloy was represented by a bilinear material model (Young’s modulus E=120GPa, yield strength σy=950MPa, tangent modulus in the plastic domain Et=0.012E, and Poisson’s ratio ν=0.3). The cut faces of the sphere section were constrained to in‐plane motion as the sphere was crushed by an analytically rigid surface.The key unknown in the challenge is the strut diameter and its variation with deposition conditions. This was inferred from comparisons of the finite element results with the experimental measurements for crushing parallel to the build direction. The results suggest that the key parameter controlling the strut diameter and the sphere crushing load is Ω = I1.31/V where I is the current and V the velocity of the electron beam. Finite element calculations were then performed for sphere loading at 60° to the build direction using the pertinent values of strut diameters in order to infer the sphere failure load.
3.9.2. Cube Crushing Model
- 1. Stress strain data for compressive samples were converted to true stress vs. plastic strain. 2. The ratio of flow stress in the R-B90 and R90B0 to the R0B0 direction was calculated from representative curves and used to define a Hill criterion yield surface with the plastic strain hardening data from the R0B0 direction. 3. The elastic modulus for each orientation was measured at stresses from 10-25 MPa and used to define orthotropic elasticity. 4. The solid walled cube was simulated using these parameters. It was assumed that the wall thickness was slightly different from the specification due to the printing process. The wall thickness in the model was adjusted to match the initial measured stiffness of the structure (adjusted wall thickness = 4.68 mm). 5. The spiral web cube was simulated (in Abaqus/EXPLICIT) assuming a 4.68 mm wall and web thickness. 6. Structural collapse was assumed to occur when the tensile failure strength in a given composite direction (20.7 MPa between build planes, 50.1 MPa between raster lines in the build plane, 62.5 MPa along the raster lines) was exceeded. The load at this point was reported as the peak load of the structure.
3.10. Submission 10: North Carolina State University
3.10.1. Cube Challenge (See Figure 28)
- Model of Buckling Load Factor (BLF) and Applied Load: Calculate BLFs using computation methods (x), employ applied load (y), compute FS bias (z), then F(x,y,z)=x*y*z. Vary material properties to fit data. Resulting
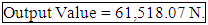
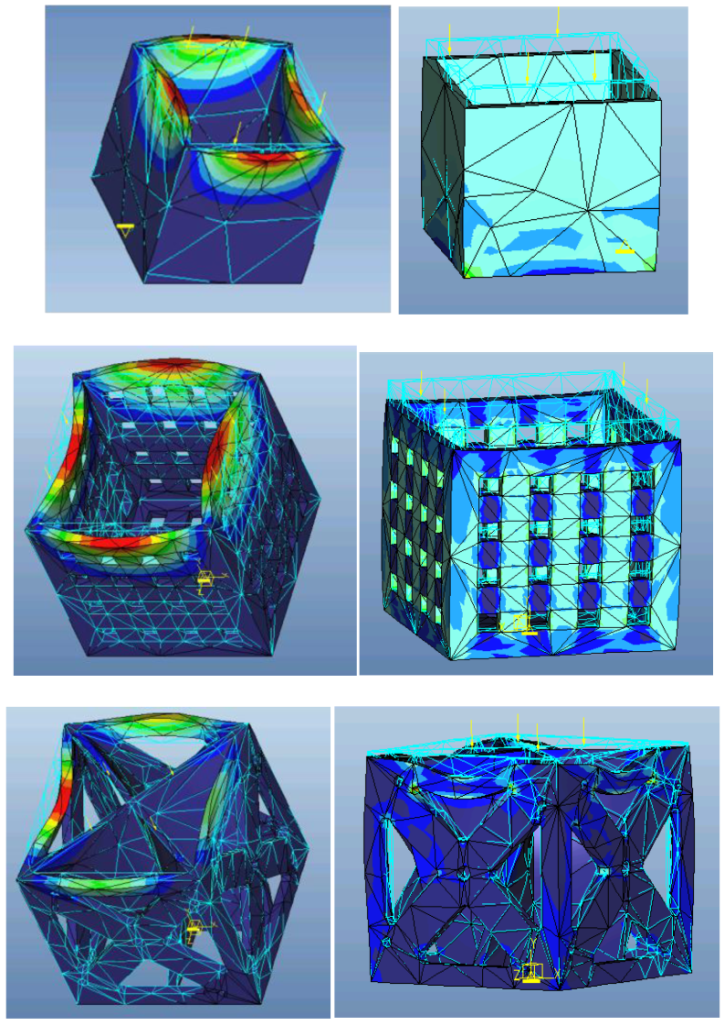 | Figure 28. Cube geometries |
3.10.2. Sphere Challenge
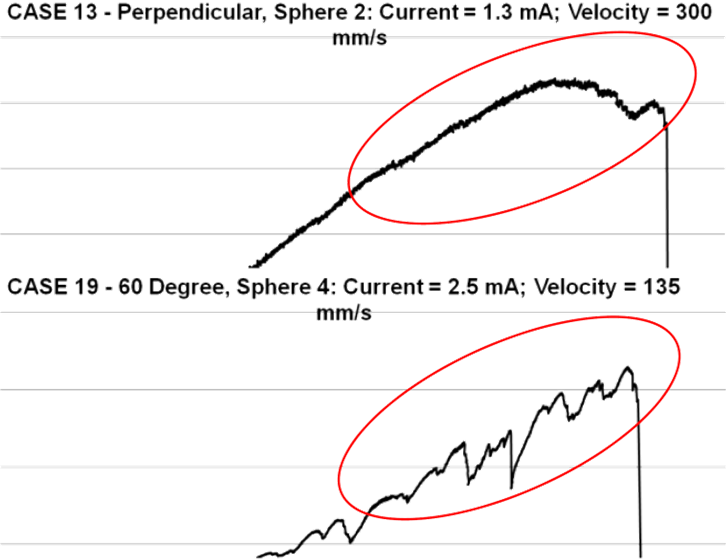 | Figure 29. Sphere crushing behavior |
3.11. Submission 11: Washington University in St. Louis
3.11.1. Titanium Sphere
- With the amount of data presented for the Titanium Sphere we were confident an accurate mathematical model could be found based solely on statistical analysis. Our program of choice to perform this analysis was the free software ‘R’. We began by importing all 9 runs for the first 17 sets of data provided on the sphere. Variables were designated as Current, Velocity, and Angle. We then used R to perform a linear regression on the data including all the cross terms of the variables. An analysis of variance showed that the only significant variables were Current, Velocity and Current*Velocity. However, the coefficients generated for these variables did not provide an accurate model. Looking at residual plots of the variables, it appeared a nonlinearity was not being accounted for in Velocity and possibly Current. We performed the analysis again this time including Velocity^2 and Current^2 terms and their crosses. Velocity^2 was divided by 1000 to make its magnitude more comparable to the other terms. An analysis of variance showed the significant terms to be Current, Velocity, Current*Velocity, Velocity^2/1000 and to a less extent Current^2. We dropped Current^2 and were left with four terms. To reduce the range of the Ultimate Stress to a smaller range we changed our model to solve for the square root of the ultimate strength. When data set 18 became available we checked our model against the given value and were satisfied with the results. We then included all 18 sets of data and solved for the coefficients again. This left us with the following equation:
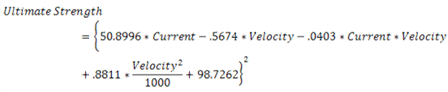 After data on the spheres crushed at 60˚ became available, we again tested our model. It gave an error of about 12% so we decided to go back and try to find a dependence on angle. Repeating the analysis, however, did not return any new significant variables. The dependence on Current^2 increased slightly so we included it in our final model:
After data on the spheres crushed at 60˚ became available, we again tested our model. It gave an error of about 12% so we decided to go back and try to find a dependence on angle. Repeating the analysis, however, did not return any new significant variables. The dependence on Current^2 increased slightly so we included it in our final model: Using this approximation the predicted value for a Sphere constructed at 2.5mA, 110mm/sec and crushed at an angle of 60° is
Using this approximation the predicted value for a Sphere constructed at 2.5mA, 110mm/sec and crushed at an angle of 60° is 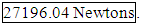
3.11.2. Polymer Cube
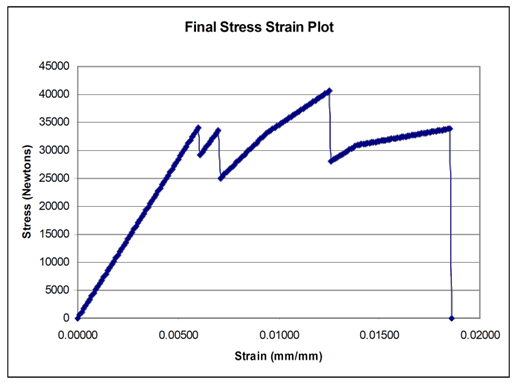
- The shape of the stress-strain curve exhibits an unusual behavior. It increases fairly linearly until it reaches its ultimate strength, common for brittle materials. Thereafter, the stress decreased with increasing strain until it could no longer support any loading. This behavior can either be attributed to strain-weakening in the material or is an artifact of the compression test method used (the material failed at the peak and the crumbled structure continued to offer some support). We concluded that the material is primarily brittle and failure coincides with the ultimate strength.
 | Figure 30. Cube stress-strain |
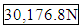

3.12. Submission 12: Lamar University
3.12.1. Sphere Model
- A kriging model based on the 20 experiment points (Average Max Load) was constructed. Pattern search was used to find a suitable set of parameters. The generated kriging model was evaluated in a MATLAB .m file containing Matlab script. The predicted strength for 60 degree, .5mA and 110 speed is
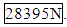
3.12.2. Cube Model
- Material Model: Linear elastic orthotropic structural material. The young’s modulus was estimated based on the cube compression test results. The strength along the raster direction is the highest (75~77 MPa), while the strength representing the bonding strength between layers are the weakest (57~59 MP), the bonding strength between raster is slightly better (61~63 MP). Since the loading is along the weakest direction, it is expected that the failure most likely to be caused by the stress along the loading direction exceed the ultimate strength of the material. A FE simulation model was built in Ansys with the following material properties: EX = 2.34 E9; EY = 1.86E9; EZ =1.97E9; Rho_xy = Rho_yz = Rho_xz = 0.48. GXY = 6.65E8; GYZ = 7.85E8; GXZ = 6.28E8. The estimated maximum load is
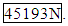
3.13. Submission 13: Team PAM (UC Irvine, Rapidtech, CalRAM)
- ASIDE: This is a note from the authors. Submission 13 has been substantially modified in form-only, but unaltered in content. The form was modified to accommodate comments by peer reviewers regarding the unwieldy presentation of regression formulas and results. These items have been reformatted by the authors merely for athletics.
3.13.1. Synopsis and Problem Statement
- The DMACE Challenge has been to determine the maximum compressive loads that can be supported by two structures manufactured by direct digital manufacturing methods. The structures were a mesh sphere manufactured by the Arcam electron beam melting process using Ti 6Al 4V and a cube with an internal structure manufactured by the Fortus 400mc 3D Printer extruded polymer process using ABS-M30. To address this challenge, a team was assembled comprising Professor Lorenzo Valdevit’s research group and others from the University of California, Irvine, Rapidtech – the leading educational organizational group for freeform fabrication, and CalRAM – the leading vendor for titanium parts built by the Arcam process in the US.
3.13.2. Overview of Modeling Approach
- The two structures were addressed using different approaches. In the case of the sphere, the team felt that the dimensions of the sphere’s detailed structure were too close to the resolution of the build technique to enable the spheres to be reliably modeled with a lattice model using known Ti 6Al 4V handbook properties; additionally, the posted data showed relatively minor anisotropy. Therefore a numerical approach based solely on provided measurements was adopted. In the case of the cube, a finite element model of the final challenge structure was built and necessary choices were made about material response in order to have a model that would run within the available time for the challenge.These approaches are described below.
3.13.3. ABS Cube
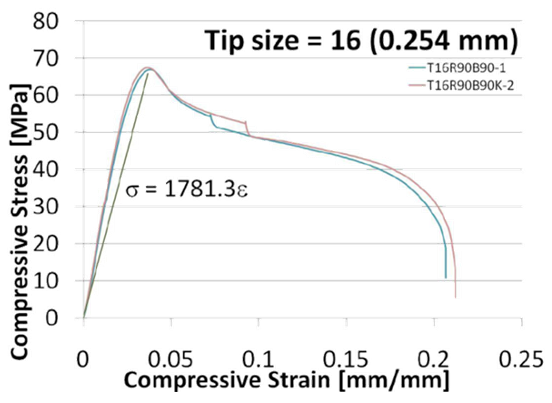
- Cube prediction methodology [Lorenzo Valdevit, valdevit@uci.edu] Tensile and compressive test data were provided for a number of samples, along three different orientations: raster direction (1), build direction (3) and the direction normal to 1 and 3 (2). The results were very reproducible, with minimal scatter. Representative stress-strain curves for a tip diameter of 0.254 mm are presented in Figure 31.
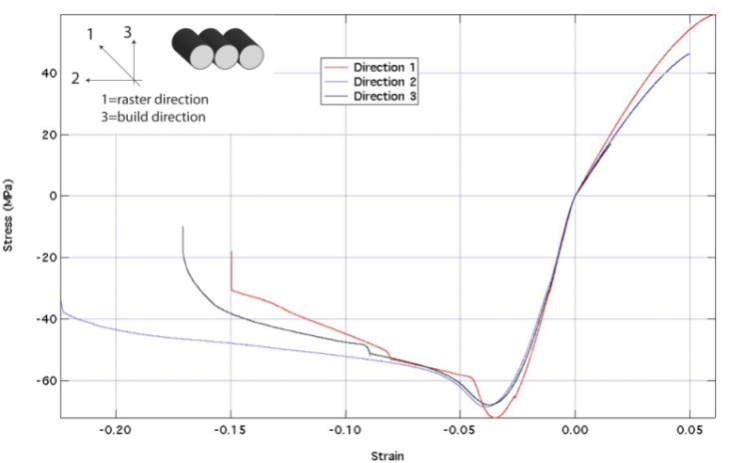 | Figure 31. Materials properties for ABS Tip 16 in tension and compression |
 | Figure 32. Geometry for the CUBE Challenge |
 | Figure 33. Mesh used for the ABAQUS simulation with shell-elements |
 | Figure 34. Load-deflection curve for the cube challenge problem. The inset shows contours of the plastic strain at the maximum load |
3.13.4. Titanium Sphere
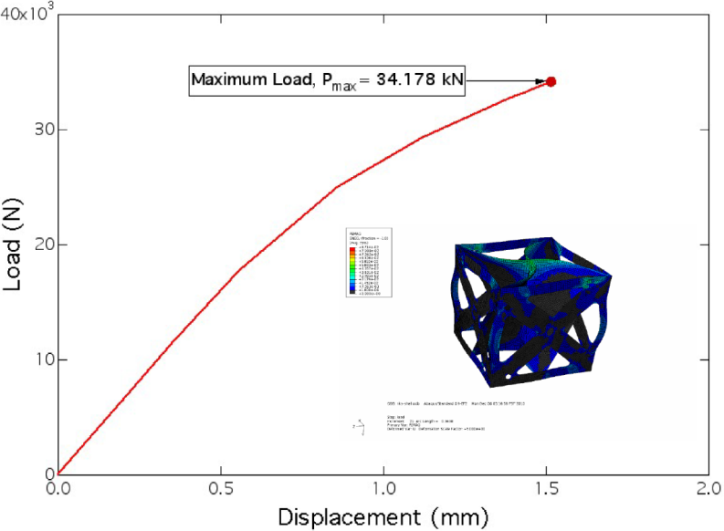
- Sphere prediction methodology [Scott Godfrey, sgodfrey@uci.edu].For prediction of failure loads for the sphere models, we implemented an interactive and resume-able multi-threaded object-oriented particle swarm optimizer written in C++ with a custom swarm particle object. The goal was identifying the best polynomial fit to the posted data as a function of three variables:
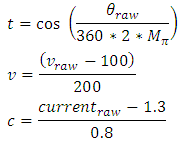 with
with 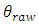 the test angle in radians,
the test angle in radians, 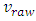 the beam velocity in mm/s, and
the beam velocity in mm/s, and 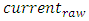 the beam current, in mA. Four different polynomials were explored (of degrees 1 to 4), resulting in 50 fitting parameters.
the beam current, in mA. Four different polynomials were explored (of degrees 1 to 4), resulting in 50 fitting parameters.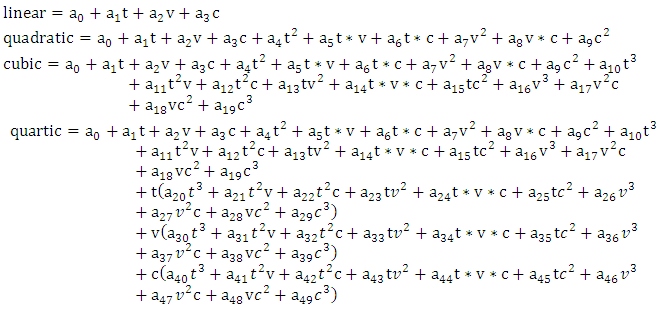 On inception, the swarm objects considered every data point supplied (160+), but an identical result was obtained using just the batch-average values for each dataset (20) on the early 'practice' problems. This close correlation in predictive results indicated that the optimizer was indeed converging on useful coefficients and the extra compute-overhead of factoring all points in the clouds was unnecessary particularly in that we were predicting batch-average values. The average error was minimized over all batch data points. The average error taken as the Euclidean length of an n-dimensional vector composed of all the individual errors. Individual errors were determined as the difference in measured load relative to the corresponding predicted load. Optimizations were considered thorough and exhausted when populations in excess of 100,000 particles operating with generational life spans of 10,000 calculation cycles failed to find any predictive 'improvements' within a complete generation. Particle integration time step (value governing particle motion in normalized parameter space) was interacted with over the course of optimizations, being varied from 1.0 down to ~0.00001 as progress stagnated. Three different sets of calculations were executed, as described below. Set1: All 20 datasets were considered with the constraint that all coefficients must be positive. Although the error was generally higher than for the other simulations, higher order polynomials (quadratic and cubic) performed best, resulting in more realistic shapes in the variables space. Additionally, all predicted loads were positive. The prediction was viable when considered relative to the nearby values. SET1:Coefficients were permitted to take on values in the range [0,+10e6]LINEAR:Average error: 5.07175e3 Predicted load: 2.0266e4 (low)Coefficients:
On inception, the swarm objects considered every data point supplied (160+), but an identical result was obtained using just the batch-average values for each dataset (20) on the early 'practice' problems. This close correlation in predictive results indicated that the optimizer was indeed converging on useful coefficients and the extra compute-overhead of factoring all points in the clouds was unnecessary particularly in that we were predicting batch-average values. The average error was minimized over all batch data points. The average error taken as the Euclidean length of an n-dimensional vector composed of all the individual errors. Individual errors were determined as the difference in measured load relative to the corresponding predicted load. Optimizations were considered thorough and exhausted when populations in excess of 100,000 particles operating with generational life spans of 10,000 calculation cycles failed to find any predictive 'improvements' within a complete generation. Particle integration time step (value governing particle motion in normalized parameter space) was interacted with over the course of optimizations, being varied from 1.0 down to ~0.00001 as progress stagnated. Three different sets of calculations were executed, as described below. Set1: All 20 datasets were considered with the constraint that all coefficients must be positive. Although the error was generally higher than for the other simulations, higher order polynomials (quadratic and cubic) performed best, resulting in more realistic shapes in the variables space. Additionally, all predicted loads were positive. The prediction was viable when considered relative to the nearby values. SET1:Coefficients were permitted to take on values in the range [0,+10e6]LINEAR:Average error: 5.07175e3 Predicted load: 2.0266e4 (low)Coefficients: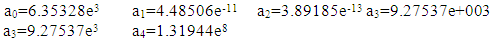 QUADRATIC:Average error: 4.89191e+003Predicted load: 2.3030e+004 (reasonable)Coefficients:
QUADRATIC:Average error: 4.89191e+003Predicted load: 2.3030e+004 (reasonable)Coefficients: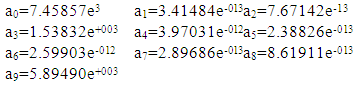 CUBIC:Average error: 4.86730e+003Predicted load: 2.3454e+004 (reasonable)Coefficients:
CUBIC:Average error: 4.86730e+003Predicted load: 2.3454e+004 (reasonable)Coefficients: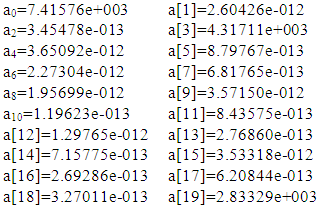 QUARTIC:Average error: 4.57712e+008Predicted load: 1.4619e+007 (NOT REASONABLE!)Coefficients:
QUARTIC:Average error: 4.57712e+008Predicted load: 1.4619e+007 (NOT REASONABLE!)Coefficients: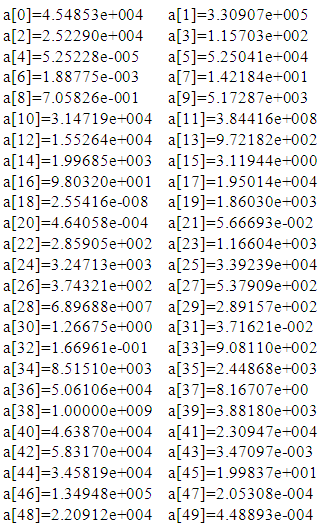 Set2: Only 6 datasets were considered with the constraint that all coefficients must be positive. The solution is similar to that of set 1, but with linear and quadratic polynomials emerging.Nearest Neighbors used (6 points):
Set2: Only 6 datasets were considered with the constraint that all coefficients must be positive. The solution is similar to that of set 1, but with linear and quadratic polynomials emerging.Nearest Neighbors used (6 points): LINEAR:Average error: 4.53880e+003Predicted load: 2.3750e+004 (reasonable)Coefficients:
LINEAR:Average error: 4.53880e+003Predicted load: 2.3750e+004 (reasonable)Coefficients: QUADRATIC:Average error: 4.53880e+003Predicted load: 2.3750e+004 (reasonable)Coefficients:
QUADRATIC:Average error: 4.53880e+003Predicted load: 2.3750e+004 (reasonable)Coefficients: CUBIC:Average error: 1.63838e+008Predicted load: 1.1703e+007 (NOT REASONABLE!)Coefficients:
CUBIC:Average error: 1.63838e+008Predicted load: 1.1703e+007 (NOT REASONABLE!)Coefficients: QUARTIC:Average error: 8.45203e+008Predicted load: 1.7148e+008 (NOT REASONABLE!)Coefficients:
QUARTIC:Average error: 8.45203e+008Predicted load: 1.7148e+008 (NOT REASONABLE!)Coefficients: Set3: All 20 datasets were considered with no constraint on the sign of the coefficients. This resulted in the smallest average error of all sets (with cubic and quartic polynomials), but also allowed for predictions of negative load values; prediction through fitting was not viable. Average errors, predicted loads, and equation coefficients for each equation are reported below:Coefficients were permitted to take on values in the range [-10E6,+10E6]LINEAR:Average error: 1.82252e+003Predicted load: 2.3997e+004 (reasonable)Coefficients:
Set3: All 20 datasets were considered with no constraint on the sign of the coefficients. This resulted in the smallest average error of all sets (with cubic and quartic polynomials), but also allowed for predictions of negative load values; prediction through fitting was not viable. Average errors, predicted loads, and equation coefficients for each equation are reported below:Coefficients were permitted to take on values in the range [-10E6,+10E6]LINEAR:Average error: 1.82252e+003Predicted load: 2.3997e+004 (reasonable)Coefficients: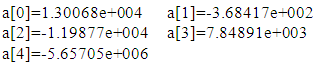 QUADRATIC:Average error: 3.05536e+002Predicted load: 2.9967e+004 (high)Coefficients:
QUADRATIC:Average error: 3.05536e+002Predicted load: 2.9967e+004 (high)Coefficients: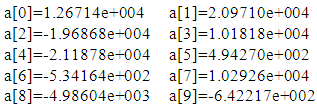 CUBIC:Average error: 5.44815e+001Predicted load: -3.1866e+005 (BAD!)Coefficients:
CUBIC:Average error: 5.44815e+001Predicted load: -3.1866e+005 (BAD!)Coefficients: QUARTIC:Average error: 2.42912e+001Predicted load: 5.8078e+004 (high)Coefficients:
QUARTIC:Average error: 2.42912e+001Predicted load: 5.8078e+004 (high)Coefficients: Based on the above, our answer for the SPHERE CHALLENGE is
Based on the above, our answer for the SPHERE CHALLENGE is 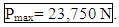
4. Summary
- Seeking to analyze output properties of digitally manufactured components DARPA executed a Challenge on the worldwide web to any and all willing participants. Participants were challenged to develop a correlation model that accurately correlates digital manufacturing (DM) machine inputs to output structural test data. Participant models were then evaluated by their ability to predict the test results of the final DM structures. Several of the participants’ predictions are listed in Table 5 and plotted in Figure 35. The model that most accurately predicted the final test results won the Challenge. Many disparate technical approaches were investigated by researchers from all over the world, and this paper introduced readers to several of those interesting technical approaches.Of deeper significance is the residual database of hundreds of material property tests performed on articles made with various input settings on typical DM hardware. This database remains freely available to worldwide researchers 0. Thus, the Challenge proves to merely be the simplest beginning.
|
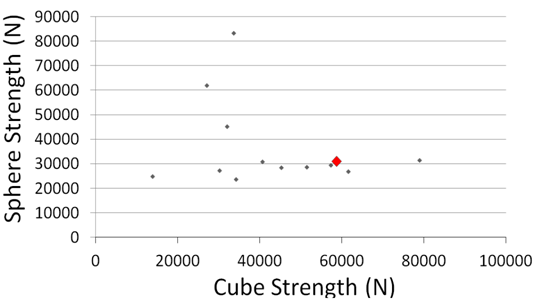 | Figure 35. Challenge participants’ predictions (true value in red) |
ACKNOWLEDGEMENTS
- The team of DARPA Fellows who conceived and executed this investigation included the author in addition to Lt Col Clinton Armani PhD, clinton.armani@us.af.mil; CDR Bill Lawerence, lefty.f14@gmail.com, Lt Col Paul Filcek, paul.filcek@us.af.mil, LTC David Rhoads, david.rhoads@us.army.mil, Joan Straub, joan.a.straub@nga.ic.gov, MAJ David Weinstein, david.weinstein@usmc.mil, and LTC Thomas Westen, twesten@cox.net. Auburn University participants include Dr. Luis Cueva-Parra, cuevadeu@yahoo.de. Data Extrapolation submission 4 participants include Robet Lenzen, e.lenzen@yahoo.com. Greystones Group participants include Jay Park Graven, jaygraven@gmail.com. Isakson Engineering participants include Dr. Steve Isakson, swi@IsaksonEngineering.com. Lamar University participants include Assistant Professor Xinyu Liu, xinyu.liu@lamar.edu. North Carolina State participants include Martin Samayoa, PhD Student, mjsamayoa@ncsu.edu. North Carolina State A&T University participants include BIEES, kj989018@ncat.edu. Pennsylvania State participants include Oyku Asikoglu,PhD Student, oxa115@psu.edu. “Snowballs Chance” submission participants include Robert Lenzen. Team Cavanaugh members include Mark Cavanaugh, mark.j.cavanaugh@gmail.com, and Dr. Steven Cavanaugh, info@iis-corp.com. Team PAM consists of the following members: John Porter (team leader) – jrporter@uci.edu; Lorenzo Valdevit (cube lead) – Valdevit@uci.edu; Scott Godfrey (sphere lead) - sgodfrey@uci.edu; Randall Schubert - randallcs@gmail.com; Eric Clough - eclough@uci.edu; Ed Tackett - etackett@rapidtech.org; Ken Patton - kpatton@rapidtech.org John Wooten - john.wooten@calraminc.com. University of California, Santa Barbara participants include Frank Zok, zok@engineering.ucsb.edu, PhD students Nell Gamble and Chris Hammetter, as well as Professor Matt Begley. University of Missouri-Columbia participants include Brian Graybill, PhD Student, bsgmr2@mail.missouri.edu. Washington University in St. Louis participants included Marcus Richards and the “Eccentric Crushers” from the Student Section of the American Society of Mechanical Engineers, marcus.richard.l@gmail.com.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML