1. Introduction

Gas-liquid annular two-phase flow is the flow which is composed of annular liquid film on the tube wall and a continuous gas core with or without liquid entrainments. Such annular flow is frequently appeared in many types of equipment, e.g., steam generators in power plants, various boilers and air conditioners. The high temperature water and refrigerant used in these equipments have lower surface tension than normal temperature water. However, the effects of surface tension on the liquid film flow behavior have never been reported besides Sadatomi et al. [1]. On the liquid film in general, there are various waves, different in behavior, such as velocity and height, and the spatial distribution of individual wave changes with time as reported by, e.g., Fukano et al. [2], Furukawa et al. [3], Al-Sarkhi et al. [4] and Sato et al. [5]. The liquid film in annular flow, therefore, shows a very complicated behavior. The structure of liquid film consisting of such complicated waves must affect not only on the gas-liquid interfacial shear stress and the flow mechanism inside the liquid film but also on the heat transfer characteristics of the liquid film flow.

Following to the above studies, the purpose of the present study is to clarify experimentally the effects of surface tension on the liquid film behavior, such as the time-spatial distribution of the liquid film thickness, the wave height, and the mean velocity and the passing frequency of the waves.

In the experiments, water and a dilute water solution of Polyoxyethylene-Laury-Ether (PLE for short), having a surface tension of 45 dyne/cm, were used as the test liquids, while air as the test gas. Why the dilute water solution of PLE was used is that it reduces the surface tension but does not induce the drag reduction as reported by Fang et al. [6]. One of the test liquid and air at room temperature and atmospheric pressure flowed co-currently vertical up in a 19.2 mm i.d. circular tube. Experimental data were obtained for the liquid film thickness, the height, the velocity and the passing frequency of the waves, the interfacial shear stress and the interfacial friction factor, in order to determine the effects of surface tension. The results of such experiments and the analyses of the respective data are presented in this paper.

2. Experimental Methods

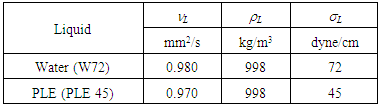
The properties of the test liquids are shown in Table 1. The kinematic viscosity (_L) and the density (_L) are nearly equal between water and the dilute water solution of PLE. The surface tension (_L) of the dilute water solution of PLE is 45 dyne/cm, about 60 % of 72 dyne/cm for the test water. These test liquids hereafter are abbreviated as PLE45 and W72 by accounting for the surface tension.

Table 1. Physical properties of test liquids at 21°C

Figure 1 shows the schematic view of the present test rig. The vertical test tube of D = 19.2 mm i.d. and about 5.4 m long, 6, was made of transparent acrylic resin. One of the two test liquids was mixed with air in an air-liquid mixer.

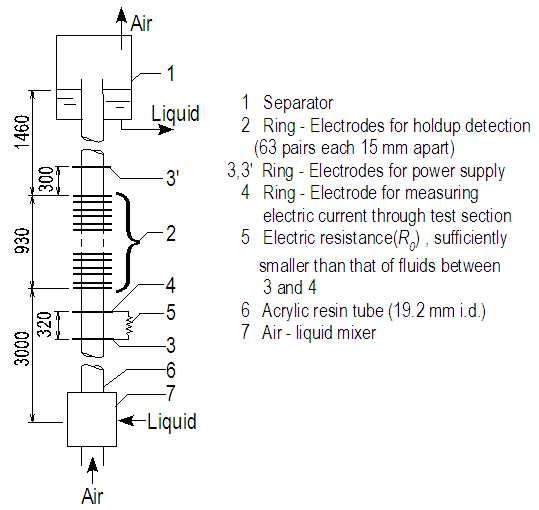Figure 1. Test rig

An air-liquid mixer, 7, consisted of 60 mm long concentric annuli, and the inner diameter of the tube was the same as that of the test tube. The liquid was injected radially into the air flow through 60 holes of 2 mm i.d. drilled on the inner tube of the annuli. The air-liquid mixture so made flowed upwards through a 3000 mm entrance section, a 930 mm measuring section and a 1460 mm discharge section, and finally flowed out to an air-liquid separator, 1. The air separated was released to atmosphere, while the liquid was returned back to a liquid storage tank upstream of a liquid circulation pump. In the measuring section, the liquid holdup was measured with the constant current method developed by Fukano [7]. Calibrations of the constant current method were conducted before and after the measurement in each run by detecting the voltage drop when the test liquid alone flows through the same test channel. The uncertainty in the liquid film measurement is estimated to be within 1%.

The detail of the liquid film measurement method was described in Furukawa’s previous paper [8]. In the present apparatus, a series of 63 pairs of holdup sensor, each 15 mm apart in axial direction, were arranged over 930 mm. A pair of the holdup sensor was composed of two 0.5 mm thick brass rings, 4.5 mm apart, embedded flush with the inner wall surface of the test tube, made from nonconductive acrylic resin of 4.5 mm thick. The output signals from the respective paired holdup sensors were converted to time-varying liquid film thickness signals (designated as t_f signals). Thus, the measured value of the respective film thickness was a circumferentially averaged value over 4.5 mm in axial length. The time-spatial distribution map, which was required to discuss the liquid film behavior in detail, was drawn up using these 63 t_f signals. Using one t_f signal or two adjacent t_f signals among 63 t_f signals, the experimental data of the wave heights, the mean value and the standard deviation of the respective wave velocities, and the passing frequency of the waves were obtained.

The flow condition in the experiment is as follows: The superficial gas velocity, j_G, ranged from 15 to 50 m/s; The superficial liquid velocity, j_L, ranged from 0.04 to 0.2 m/s; The system pressure at a middle point of the measuring section was 0.110 to 0.128 MPa; Test liquids temperatures were controlled at 21±1°C. The surface tension of the test liquid was measured before and after the experiments and the difference between them was within 3%.

3. Experimental Result and Discussions

3.1. Liquid Film Behaviour

Figure 2 show the time-spatial characteristics map (referred to as TS map in this paper) of the liquid film thickness, t_f, respectively for (a) air-W72 and (b) air-PLE45. In the TS map, t_f signals from 63 pair holdup sensor are simultaneously shown on the respective axial distances with the same ordinate scale. The liquid film thickness, t_f, is calculated by substituting the liquid holdup, 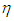, data into the following equation:

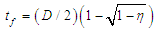(1)

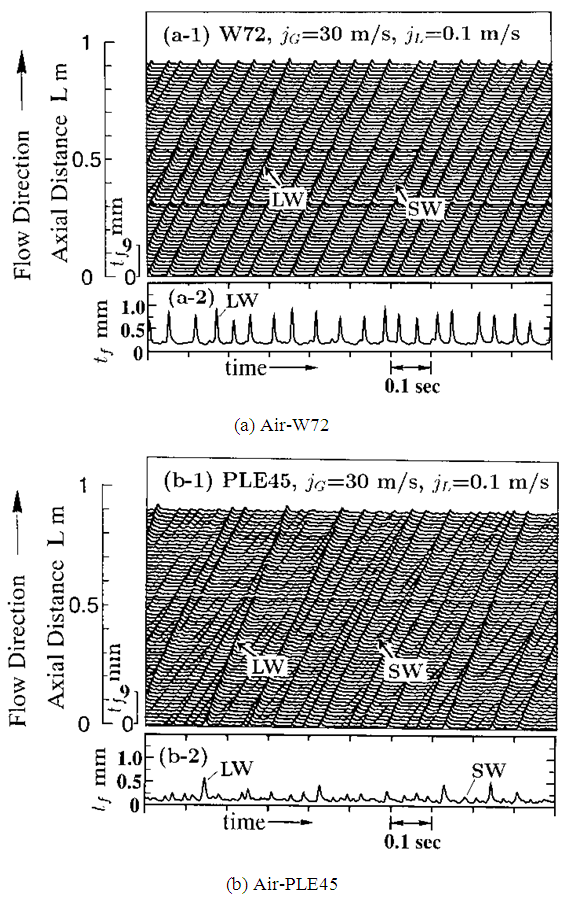Figure 2. Time-spatial characteristics map of liquid film thickness for air-W72 and air-PLE45

In Figure 2 wave veins, which is the traces formed by individual wave flowing upwards, are observed. The gradient of each wave vein means the velocity of the wave, and steeper the gradient higher the wave velocity.

The signs “SW” and “LW” in each figure represent the small wave and the large wave. Fukano et al. [9] proposed a model for a liquid film flow in a horizontal air-water annular flow. According to their model, the liquid film flow consists of disturbance wave and a continuous liquid film. The liquid film besides waves is named as a base film, and the ripples formed on the base film are named as a base wave. LW called in the present paper corresponds to the disturbance wave, often appeared in air-water flows. The reason why the “LW” is used in the present paper is that the LW in air-PLE45 system as well as in air-liquid with higher viscosity system as reported by Furukawa [8] shows different velocity characteristics from the disturbance wave seen in air-water system. In addition, SW is used as synonymous with the base wave. The discrimination between LW and SW was based upon their behavior in the TS map in Figure 2; LW is a clearly discernible large wave which exists more than 0.93 m, being the wave detection zone, while SW is a small wave frequently generated from the rear side of LW and captured and absorbed by the subsequent LW, thus relatively short in existing time or distance. Thus, LW is defined as the large wave whose wave vein was kept over the measuring section of 0.93 m in TS map, while SW is the wave whose wave vain was not kept.

The LWs for W72 have uniformities in velocity, height and axial spacing between them. While, for PLE45, such uniformities disappear and the wave height became low.

The number of SWs increased for PLE45, and the surface of the base film became rougher and denser like sharkskin and the film thickness became thinner than W72. In addition, as can be seen from the gradient of wave veins of SWs, the wave velocities of SWs for PLE45 became faster than those for W72, meaning that the mean velocity of the base film increased with decreasing of surface tension. This is mainly caused by the increase in the interfacial friction force due to the sharkskin-like interface by a huge number of SW. As written in “Handbook of Gas-Liquid Two-Phase Flow Technology [10]”, the liquid entrainment to the gas core increases with decreasing of surface tension, thus the film thickness may become somewhat thinner by the entrainment. However, the entrainment rate in PLE45 is considered to be a few since the SW in PLE45 is similar to a ripple wave, being different from a disturbance wave generating the entrainment. Thus, the interfacial shear stress for PLE45 becomes higher than W72, and the resistance of flow was dominated by the denser SWs on the base film. In order to confirm the above consideration, we are planning to measure the entrainment rate in our future study.

As can be seen in the TS map for W72, the wave heights of LW and SW are extremely different. Therefore, it is easy to judge which wave is LW or SW from the t_f signal alone. However, t_f signal for PLE45 differs remarkably from that for W72 in a time-varying aspect, and a few SW with a similar height to LW sometimes exists. Thus, in order to surely discriminate LWs from SWs, it is quite important to observe a lot of t_f signals at different locations in the TS map.

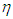Figure 3 and 4 show an example of the time variation data of liquid holdup, , for PLE45 at j_G = 20 m/s and j_L = 0.1 m/s, and the corresponding passing frequency of each wave with different height. The frequency for W72 is also shown in Figure 4. The passing frequency, 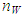, was determined by the number of waves intersecting the line of arbitrary holdup value, 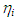, in Figure 3 per unit sampling time. The abscissa of Figure 4, t_f, is determined from 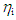value by substituting into Eq. (1).

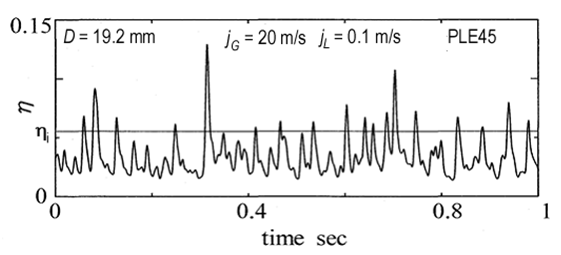Figure 3. Example of time variation data of liquid holdup signal,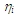

Figure 4. Effects of surface tension on passing frequency of each wave with different height

The shape of the passing frequency for W72 in Figure 4 takes distorted trapezoidal form, while that for PLE45 takes a single-peaked form. In addition, the base film thickness, t_fB, is defined as the thickness when the passing frequency takes the maximum value.

Figure 5 shows the change in the base film thickness, t_fB, against j_G at a fixed condition of j_L = 0.1 m/s. Solid curve and broken curve are calculations for W72 and PLE45 by Sekoguchi et al.’s correlation [11] based on air-water upward flow data in 8 and 12, 18 and 26 mm i.d. vertical pipes. t_fB for PLE45 is thinner than that of W72, and the difference of t_fB between PLE45 and W72 increases with decreasing of j_G. A comparison of t_fB between the present data and the calculations shows that there is qualitative agreement but not quantitative, and the disagreement between them increases with decreasing of j_G. Similar disagreement is also seen at other j_L conditions. Thus, Sekoguchi et al.’s correlation has a room of improvement, especially for the effects of surface tension at low j_G region of j_G < 40 m/s.

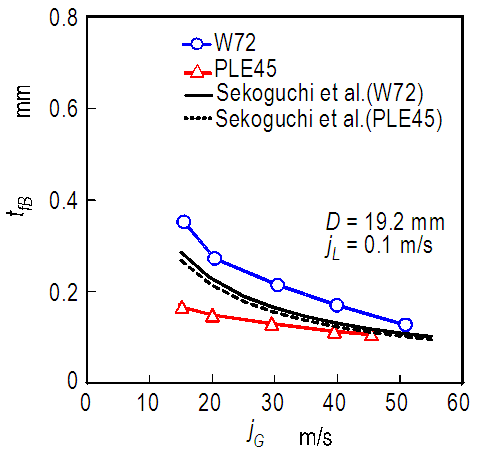Figure 5. Effects of surface tension on base film thickness, tfB

3.2. Mean Values of Wave Velocities and Passing Frequencies for LW and SW

Figure 6 shows the calculation method of the velocity and the passing frequency of individual wave in LWs and SWs in the TS map. Firstly, we picked up two t_f signals from arbitrary two adjacent holdup sensors, each L_P = 15 mm apart in axial direction. After studying the existing time or distance of individual wave, we discriminated LW from SW. Secondly, we calculate the transit time, t_P, for example, A to A’, by a cross-correlation of the two waves. Finally, we determine the velocity of wave A, u_W, as follows.

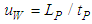(2)

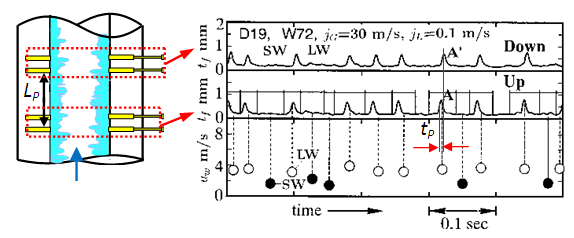Figure 6. Example of tf signals at two adjacent axial positions for determination of each wave velocity

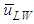Similarly, the arithmetic mean velocities of the respective LWs and SWs which appear in the sampling time were determined. The mean velocities for LWs and SWs, and 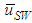, and the passing frequencies, N_LW and N_SW, were obtained as follows.

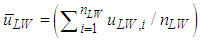(3)

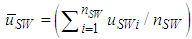(4)

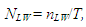(5)

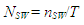(6)

Here, u_LWi and u_SWi are the velocities of individual LW and SW, T the sampling time, and n_LW and n_SW the total numbers of LWs and SWs appeared within the sampling time.

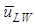Figure 7 shows the present data on the respective mean wave velocities for LWs and SWs, and 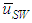at a fixed j_L = 0.1 m/s. Also plotted as asterisk symbols are Nakasatomi’s data for air-water upward flows in a 25 mm i.d. vertical pipe [12]. Solid curve and broken curve are calculations by Sekoguchi et al.’s correlation [11]. Both 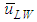and 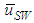increased with j_G, and 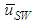for PLE45 became much faster than that for W72 at the same j_G. 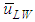for PLE45, however, became a little faster than that for W72. In addition, the present 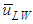data agree well with the Nakasatomi’s data irrespective of the difference in pipe diameter. 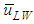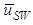From a comparison of and for PLE45 and W72, the difference in the mean velocity between LWs and SWs for W72 is larger than that for PLE45. Similar tendency was also seen at other j_L conditions. The cause of these is probably that the drag force on SW by air flow in the gas core is stronger for PLE45 depending on the denser SWs on the base film as mentioned before.

Figure 7. Effects of surface tension on mean wave velocities, respectively for LWs and SWs

Figure 8 shows the passing frequency data for LW and SW, N_LW and N_SW against j_G at a fixed j_L = 0.1 m/s. Solid curve and broken curve are calculations by Sekoguchi et al.’s correlation [11]. For W72 N_LW is higher than N_SW, while for PLE45 N_LW is lower than N_SW. N_LW for PLE45 became lower than that for W72, the difference of N_LW between W72 and PLE45 increases with j_G. 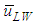A comparison between the present data of and N_LW and the calculations shows qualitative agreement between them for W72. For PLE45, on the other side, the agreement of 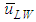between them is not quantitative, and the agreement of N_LW is bad. The cause of these is probably that Sekoguchi et al.’s correlation was based only on air-water data despite the correlation contains a surface tension term. Thus, Sekoguchi et al.’s correlation has a room of improvement.

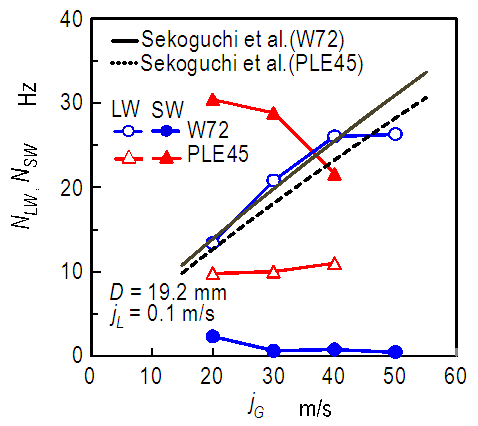Figure 8. Effects of surface tension on passing frequencies, respectively for LWs and SWs

The changes in the liquid film behavior, the wave velocity and the passing frequency caused by the reduction of surface tension described above seem to affect the gas-liquid interfacial shear stress.

3.3. Gas-liquid Interfacial Shear Stress

Figure 9 shows the gas-liquid interfacial shear stress data, 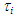, and the mean liquid velocity data, 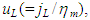against j_G at a fixed j_L = 0.1 m/s. Here, 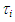data were determined from force balance equation in the gas core by neglecting hydrostatic head loss, i.e., determined by substituting pressure drop data, - dp/dz, into:

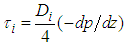(7)

Figure 9. Effects of surface tension on interfacial shear stress,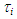

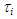Here, D_i is the diameter of gas-liquid interface and calculated by subtracting twice of the mean liquid film thickness t_fm from the pipe diameter, D_i = D - 2 t_fm. increased with j_G irrespective of difference in test liquid because the drag force on gas-liquid interface increase with j_G. In addition, 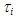for PLE45 is larger than that of W72, because the liquid film surface for PLE45 became rougher with denser SWs like sharkskin than that for W72 as described in section 3.1. From the liquid film behavior in Figure 2, we believe that the effects of the denser SWs for PLE45 are larger than those of the sparser LWs for W72 on the interfacial shear stress. Furthermore, the mean liquid velocity, u_L, for PLE45 is faster than that for W72 at all j_G in Figure 9. Similar trend was also seen at other j_L conditions.

3.4. Gas-Liquid Interfacial Friction Factor

If we assume no liquid entrainment in the gas-core, we can determine the gas-liquid interfacial friction factor, 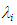, by substituting experimental data on the gas density, 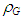, the mean gas velocity, u_G, and the gas-liquid interfacial velocity, u_i, into the following equation:

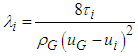(8)

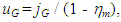Here, u_G can be determined from where the mean liquid hold up can be determined as 1 - (1 - 2t_fm / D)². Since the mean value of the measured wave velocity was much slower than u_G, the interfacial velocity, u_i, is negligible in comparison to u_G. In addition, 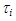was determined from Eq. (7). Thus, in the present study, Eq. (8) is reduced to:

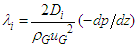(9)

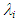Figure 10(a) shows the gas-liquid interfacial friction factor data, , against the superficial gas Reynolds number, 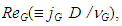at a fixed j_L of 0.1 m/s. Besides the present data for W72 and PLE45, Nakasatomi’s data for air-water upward flows in a 25 mm i.d. vertical pipe [12] are simultaneously plotted as square symbols. The trend of his data is similar to that of the present data, but his data is about 40% higher than the present data for W72, probably due to the difference in pipe diameter.

Also shown on Figure 10(a) is the curve calculated by Blasius’ equation for single-phase turbulent flow in a pipe with hydraulically smooth wall:

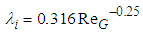(10)

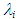The respective data mentioned above show similar trends to the calculated curve by Blasius’ equation, but they show much higher value because of interfacial waves. In addition, the present data for PLE45 show higher value than that for W72, because the liquid film surface for PLE45 became rougher and denser like sharkskin than that for W72, as described in relation to Figure 2.

Regarding the interfacial friction factor, 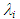, various correlations have been proposed so far. So, in the present study the correlations by Wallis [13], Moeck [14], Akagawa [15], Hori et al. [16], Fukano et al. [2] and Fore et al. [17] were tested against the present data.

In Figure 10(a), calculated results by Akagawa’s correlation [15], Eq. (11), and Hori et al.’s correlation [16], Eq. (12), are drawn respectively as heavy solid and broken curves.

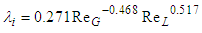(11)

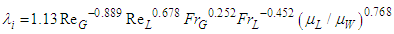(12)

Here,

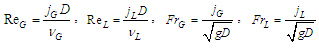(13)

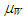In Eq. (12), is the viscosity of water at 20°C. Eq. (11) was based on air-water upward annular-mist flow data in 50.8 mm i.d. vertical pipe by Chien et al. [18]. The gas and the liquid Reynolds numbers covered were 70000 < Re_G < 350000 and 1250 < Re_L < 22100. On the other side, Eq. (12) was based on air-aqueous solution of glycerin upward annular ripple flow data in 19.8 mm i.d. vertical pipe. The kinematic viscosity of the aqueous solution was 10^-5 m²/s, and the gas and the liquid Reynolds numbers covered were 15000 < Re_G < 85000 and 5 < Re_L < 55.

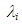data for W72 are higher than those determined by Eq. (11) and (12), but approach Eq. (11) as Re_G increases. The cause of the difference in 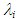between W72 data and Eq. (12) is probably due to the difference in wave structure, i.e., disturbance wave for W72 data and ripple for Eq. (12). On the other side, 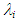data for PLE45 are two-times (or four-times) or more higher than those determined by Eq. (11) (or (12)) though the wave structure for PLE45 is similar to ripple since the waves for PLE45 mainly consist of SWs.

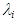correlations as a function of the mean liquid film thickness, t_fm, have been proposed by Wallis [13], Eq. (14), Moeck [14], Eq. (15), Fore et al. [17], Eq. (16), and Fukano et al. [2], Eq. (17):

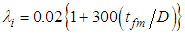(14)

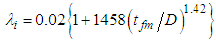(15)

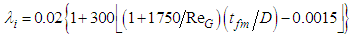(16)

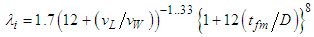(17)

Eq. (14) and (15) are mainly based on air-water upward annular disturbance wave flow data. Eq. (16) is based on nitrogen-water upward annular flow data in a 5.08×101.6 mm rectangular duct.

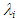In Fig. 10(b), calculated results of , by these correlations are drawn as six kinds of different curves against t_fm/D. Eqs. (14) – (16) cannot fit the PLE45 data but can fit reasonably well the W72 data. Eq. (17) was based on systematic experiments using high viscosity liquids as the test liquid and includes liquid viscosity ratio to water at 20°C, . Eq. (17), however, over-predicts a little the W72 data, and under-predicts the PLE data. Thus, all these four equations cannot fit PLE45 data. Since the difference between the calculations and the PLE data increase with (t_fm/D), Fore et al.’s correlation [17], Eq. (16), is tentatively modified by including 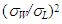ratio in the present study as follows:

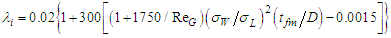(18)

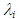Eq. (18) for the PLE45, drawn as heavy solid curve, can fits reasonably well with the PLE45 data though it is tentative. In order to further improve correlation, we must collect 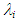and t_fm data using a variety of liquids with different properties and different diameter test pipes in our future studies.

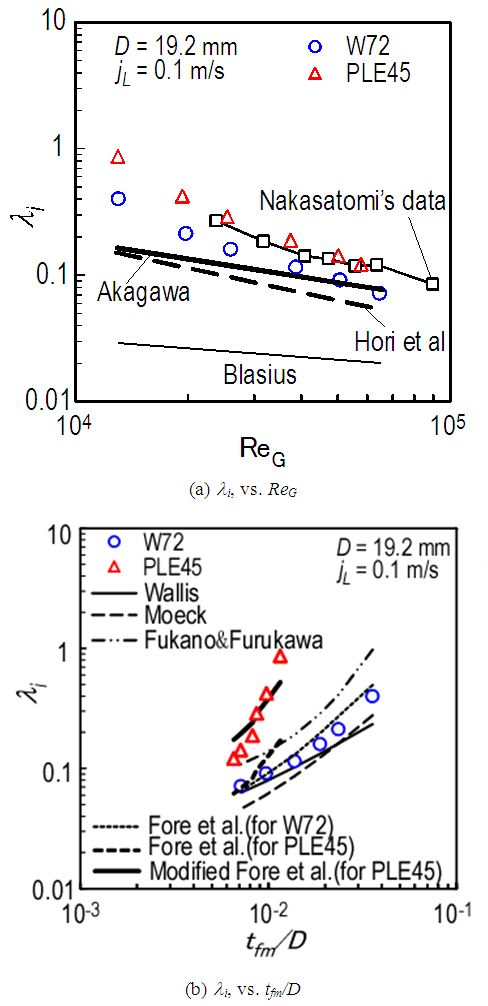Figure 10. Comparison of interfacial friction factor between experimental data and calculations by several correlations

4. Conclusions

In order to clarify the effects of surface tension on liquid film behaviour, experiments were conducted for upward annular flow in a 19.2 mm i.d. vertical pipe. As the test liquids, water and a dilute water solution of PLE were used. Main findings are as follow:

1. By the reduction of surface tension, the passing frequency of LWs decreased, while that of SWs extremely increased. The surface of the base film for PLE45 became rougher and denser like sharkskin, and the film thickness became thinner than W72.

2. Mean wave velocity of SWs, 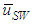, for PLE45 became much faster than that for W72. That of LWs, 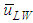, for PLE45, however, became a little faster than that for W72. Thus, the difference in velocity between LWs and SWs for W72 was higher than that for PLE45.

3. The interfacial shear stress,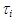 , for PLE45 was larger than that of W72, because the liquid film surface for PLE45 became rougher and denser like sharkskin. The effects of denser SWs for PLE45 must be larger than those of sparser LWs for W72 on the interfacial shear stress.

4. For interfacial friction factor,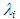 , Akagawa’s and Hori et al.’s correlations under-predict the present data for W72, but that by Akagawa approaches as Re_G increases. Wallis’s, Moeck’s and Fore et al.’s correlations could not fit the PLE45 data but could fit reasonably well the W72 data. Fukano et al.’s correlation over-predicts a little the W72 data, and under-predicts the PLE data.

5. Modified Fore et al.’s correlation proposed in the present study, which include surface tension effect, could fit reasonably well with the PLE45 data though it is tentative. In order to further improve 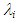correlation, we must collect 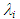and t_fm data using a variety of liquids with different properties and different diameter test pipes in our future studies.