| [1] | S. Halelfadl, T. Maré and P. Estellé, “Efficiency of carbon nanotubes water based nanofluids as coolants,” Experimental Thermal and Fluid Science, vol. 53, pp. 104-110, 2014. |
| [2] | M. Kole and T. Dey, “Viscosity of alumina nanoparticles dispersed in car engine coolant,” Experimental Thermal and Fluid Science, vol. 34, no. 6, p. 677–683, 2010. |
| [3] | N. A. C. Sidik, M. N. A. W. M. Yazid and R. Mamat, “A review on the application of nanofluids in vehicle engine cooling system,” International Communications in Heat and Mass Transfer, vol. 68, p. 85–90, 2015. |
| [4] | F. T. Ndoye, P. Schalbart, D. Leducq and G. Alvarez, “Numerical study of energy performance of nanofluids used in secondary loops of refrigeration systems,” International Journal of Refrigeration, vol. 52, pp. 122-132, 2015. |
| [5] | S.-s. Bi, S. Lin and L.-l. Zhang, “Application of nanoparticles in domestic refrigerators,” Applied Thermal Engineering, vol. 28, no. 14-15, p. 1834–1843, 2008. |
| [6] | S. Bi, K. Guo, Z. Liu and J. Wu, “Performance of a domestic refrigerator using TiO2-R600a nano-refrigerant as working fluid,” Energy Conversion and Management, vol. 52, no. 1, p. 733–737, 2011. |
| [7] | R. Padmini, P. V. Krishna and G. K. M. Rao, “Effectiveness of vegetable oil based nanofluids as potential cutting fluids in turning AISI 1040 steel,” Tribology International, vol. 94, pp. 490-501, 2016. |
| [8] | C. Chan, W. Lee and H. Wang, “Enhancement of surface finish using water-miscible nano-cutting fluid in ultra-precision turning,” International Journal of Machine Tools and Manufacture, vol. 73, p. 62–70, 2013. |
| [9] | A. K. Sharma, A. K. Tiwari and A. R. Dixit, “Improved Machining Performance with Nanoparticle Enriched Cutting Fluids under Minimum Quantity Lubrication (MQL) Technique: A Review,” Materials Today: Proceedings, vol. 2, no. 4-5, p. 3545–3551, 2015. |
| [10] | O. A. Alawi, N. A. C. Sidik and M. Beriache, “Applications of nanorefrigerant and nanolubricants in refrigeration, air-conditioning and heat pump systems: A review,” International Communications in Heat and Mass Transfer, vol. 68, pp. 91-97, 2015. |
| [11] | P. Kalita, A. P. Malshe, A. S. Kumar, V. Yoganath and . T. Gurumurthy, “Study of specific energy and friction coefficient in minimum quantity lubrication grinding using oil-based nanolubricants,” Journal of Manufacturing Processes, Sp.Ed. Micro and Nano Manufacturing, vol. 14, no. 2, pp. 160-166, 2012. |
| [12] | H. Chang, Z. Li, M. Kao, K. Huang and H. Wu, “Tribological property of TiO2 nanolubricant on piston and cylinder surfaces,” Journal of Alloys and Compounds, vol. 495, no. 2, pp. 481-484, 2010. |
| [13] | C. S. Marcano, S. Bensaid, F. Deorsola, N. Russo and D. Fino, “Nanolubricants for diesel engines: Related emissions and compatibility with the after-treatment catalysts,” Tribology International, vol. 72, p. 198–207, 2014. |
| [14] | H. Chen, Y. Ding and C. Tan, “Rheological behaviour of nanofluids,” New Journal of Physics, vol. 367, no. 9, 2007. |
| [15] | M. Akbulut, “Nanoparticle-Based Lubrication Systems,” Journal of Powder Metallurgy & Mining, vol. 1, no. 1, 2012. |
| [16] | Y. Wu, W. Tsui and T. Liu, “Experimental analysis of tribological properties of lubricating oils with nanoparticle additives,” Wear, vol. 262, pp. 819-825, 2007. |
| [17] | K. P. Nair, S. M. Ahmed and S. T. Al-qahtani, “Static and dynamic analysis of hydrodynamic journal bearing operating under nano lubricants,” International Journal of Nanoparticles, vol. 2, no. No.1/2/3/4/5/6, pp. 251-262, 2009. |
| [18] | B. Shenoy, K. G. Binu, R. Pai, D. S. Rao and R. S. Pai, “Effect of nanoparticles additives on the performance of an externally adjustable fluid film bearing,” Tribology International, Vols. 38-42, p. 45, 2012. |
| [19] | K. G. Binu, B. S. Shenoy, D. S. Rao and R. Pai, “Stability characteristics of journal bearing systems lubricated with couple stress fluids using the nonlinear transient approach,” Journal of Tribology and Surface Engineering, vol. 3, no. 1/2, pp. 51-66, 2013. |
| [20] | K. Yathish, K. G. Binu, R. S. D’Silva, B. S. Shenoy, and R. Pai, “Static Characteristics of Two-Axial Groove Journal Bearing Operating on TiO2 Nanolubricant”, Journal of Mechanical Engineering and Automation, pp. 94-99, 2015. |
| [21] | K. Kadam, S.S. Banwait, and S.C. Laroiya, “Thermo hydrodynamic analysis of plain journal bearing with modified viscosity temperature equation”, International Journal of Mechanical Engineering and Technology (IJMET), Vol. 5, pp. 31, 2014. |
| [22] | S. Torgal and R. Saini, “Thermo-Hydrodynamic Analysis of Journal Bearing To Find Out Equivalent Temperature”, International Journal of Science Technology & Engineering, Vol. 1, 2015. |
| [23] | K. H. Bagul, P. N. Patil and R. Y. Patil, “Thermal Analysis of Journal Bearing Using CFD Software for Performance Enhancement”, International Journal of Science Technology & Engineering, Vol. 3, 2017. |
| [24] | M. Spoorthi, K. Prajwal, K. G. Binu, Neil Vaz, Rolvin D’Silva1, and R. Pai, “Formulation and Viscosity Analysis of TiO2 Nanoparticle”, American Journal of Materials Science, pp. 198-202, 2015. |
| [25] | K.G. Binu, B.S. Shenoy, D.S. Rao, and R. Pai, “Static charac-teristics of a fluid film bearing with TiO2 based nanolubricant using the modified Krieger–Dougherty viscosity model and couple stress model”, Tribology International, Vol.75, pp.69-79, 2014. |
| [26] | H. Chen, Y. Ding and C. Tan, “Rheological behaviour of nanofluids,” New Journal of Physics, vol. 367, no. 9, 2007. |


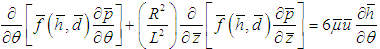
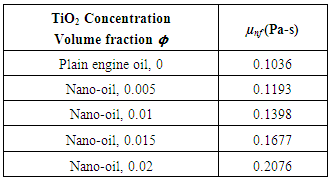
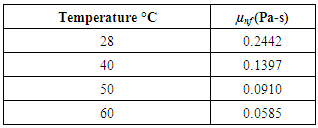
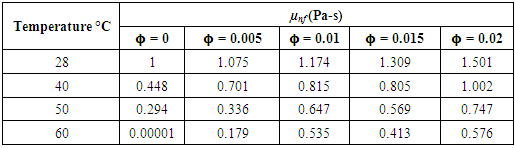
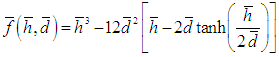 In solving the above Reynolds equation to obtain the static bearing performance characteristics, the temperature adjusted nanolubricant viscosities at different concentrations are utilized. The final viscosities considered for analysis will the difference of viscosities simulated using modified Krieger-Dougherty Model and viscosities simulated using a temperature dependent empirical model published by Spoorthi et al. [24] for TiO2 dispersions in Engine oil. The viscosity models utilized in the study are described in detail below.
In solving the above Reynolds equation to obtain the static bearing performance characteristics, the temperature adjusted nanolubricant viscosities at different concentrations are utilized. The final viscosities considered for analysis will the difference of viscosities simulated using modified Krieger-Dougherty Model and viscosities simulated using a temperature dependent empirical model published by Spoorthi et al. [24] for TiO2 dispersions in Engine oil. The viscosity models utilized in the study are described in detail below.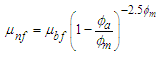
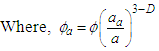
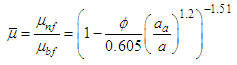
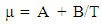
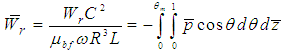
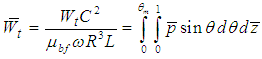
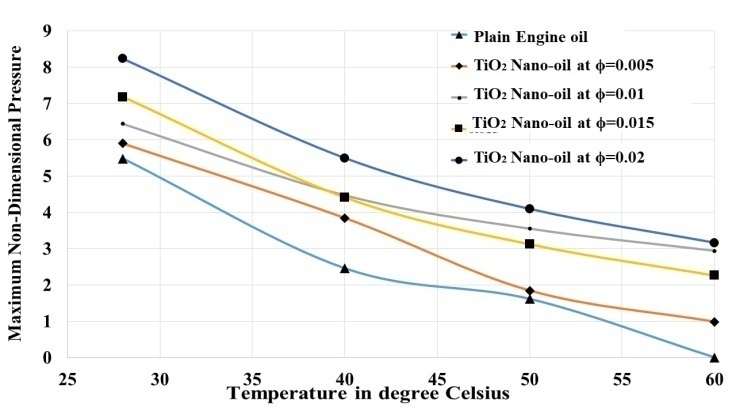
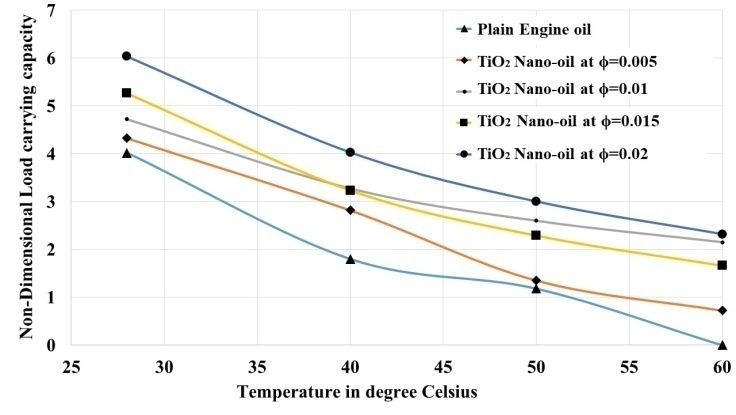
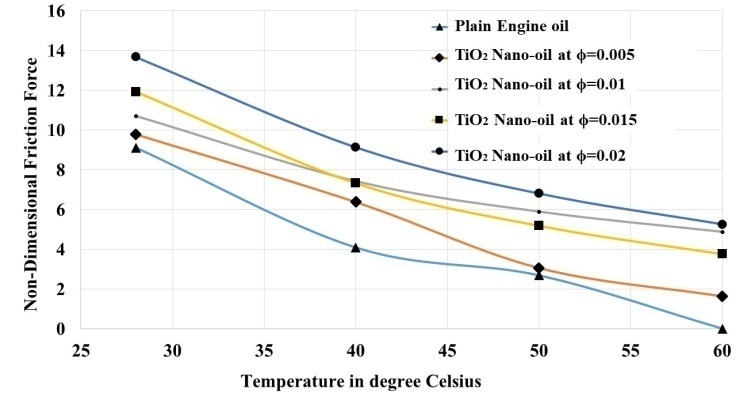
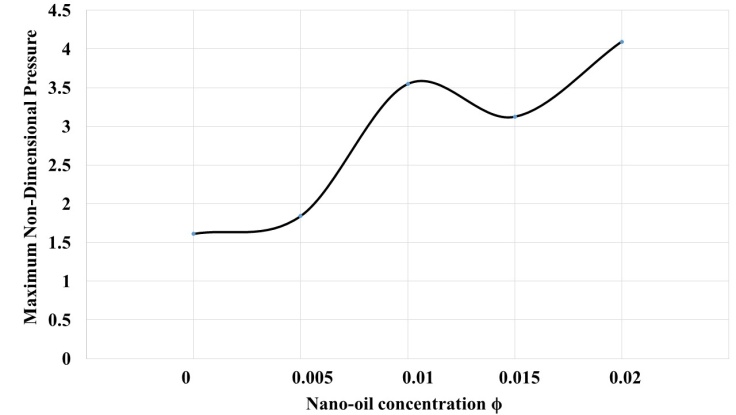
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML