| [1] | Zhaosheng Feng, Goong Chen, Sze-Bi Hsu, “A Qualitative Study of the Damped Duffing Equation and Applications”, University of Texas-Pan American, Edinburg, TX, 2005. |
| [2] | Tamas Kalmar, Balakumar Balachandran, “Forced Harmonic Vibration of a Duffing Oscillator with Linear Viscous Damping-Nonlinear Oscillators and their Behavior”, First Edition, Published John Wiley & Sons, Ltd. ISBN: 978-0-470-71549-9, 2011. |
| [3] | Liao, S.J. and Cheung, A.T. ‘‘Application of homotopy analysis method in nonlinear oscillations’’, ASME Journal of Applied Mechanics, 65, pp. 914–922 (1998). |
| [4] | Mickens, R.E. ‘‘Mathematical and numerical study of the Duffing-harmonic oscillator’’, Journal of Sound and Vibration, 244, pp. 563–567 (2001). |
| [5] | He, J.H. ‘‘Homotopy perturbation technique’’, Computer Methods in Applied Mechanics and Engineering, 178, pp. 257–262 (1999). |
| [6] | Younesian, D., Askari, H., Saadatnia, Z. and Yazdi, M.K. ‘‘Free vibration analysis of strongly nonlinear generalized Duffing oscillators using He’s variational approach & homotopy perturbation method’’, Nonlinear Science Letters A, 2, pp. 11–16 (2011). |
| [7] | Ganji, D.D., Alipour, M.M., Fereidoon, A.H. and Rostamiyan, Y. ‘‘Analytic approach to investigation of fluctuation and frequency of the oscillators with odd and even nonlinearities’’, IJE Transactions A, 23, pp. 41–56 (2010). |
| [8] | He, J.H. ‘‘Comment on He’s frequency formulation for nonlinear oscillators’’, European Journal of Physics, 29, pp. 19–22 (2008). |
| [9] | He, J.H. ‘‘Preliminary report on the energy balance for nonlinear oscillations’’, Mechanics Research Communications, 29, pp. 107–111 (2002). |
| [10] | Ganji, D.D., Gorji, M., Soleimani, S. and Esmaeil pour, M. ‘‘Solution of nonlinear cubic-quintic Duffing oscillators using He’s energy balance method’’, Journal of Zhejiang University: Science A, 10, pp. 1263–1268 (2009). |
| [11] | Durmaz, S., Demirbag, S.A. and Kaya, M.O. ‘‘High order He’s energy balance method based on collocation method’’, International Journal of Nonlinear Sciences and Numerical Simulation, 11, pp. 1–5 (2010). |
| [12] | He, J.H. ‘‘Max-min approach to nonlinear oscillators’’, International Journal of Nonlinear Sciences and Numerical Simulation, 9, pp. 207–210 (2008). |
| [13] | Yazdi, M.K., Ahmadian, H., Mirzabeigy, A. and Yildirim, A. ‘‘Dynamic analysis of vibrating systems with nonlinearities’’, Communications in Theoretical Physics, 57, pp. 183–187 (2012). |
| [14] | Khan, Y., Akbarzade, M. and Kargar, A. ‘‘Coupling of homotopy and the variational approach for a conservative oscillator with strong odd nonlinearity’’, Scientia Iranica, 19, pp. 417–422 (2012). |
| [15] | Yazdi, M.K., Mirzabeigy, A. and Abdollahi, H. ‘‘Nonlinear oscillators with non-polynomial and discontinuous elastic restoring forces’’, Nonlinear Science Letters A, 3, pp. 48–53 (2012). |
| [16] | Wu, B.S. and Sun, W.P. ‘‘Construction of approximate analytical solutions to strongly nonlinear damped oscillators’’, Archive of Applied Mechanics, 81, pp. 1017–1030 (2011). |
| [17] | Cveticanin, L. ‘‘Oscillators with nonlinear elastic and damping forces’’, Computers & Mathematics with Applications, 62, pp. 1745–1757 (2011). |
| [18] | Leung, A.Y.T., Guo, Z. and Yang, H.X. ‘‘Residue harmonic balance analysis for the damped Duffing resonator driven by a van der Pol oscillator’’, International Journal of Mechanical Sciences, 63, pp. 59–65 (2012). |
| [19] | Turkyilmazoglu, M. ‘‘An effective approach for approximate analytical solutions of the damped Duffing equation’’, PhysicaScripta, (2012), http://dx.doi.org/10.1088/0031-8949/86/01/015301. |
| [20] | Elias-Zungia, A. ‘‘Analytical solution of the damped Helmholtz–Duffing equation’’, Applied Mathematics Letters, 25, pp. 2349–2353 (2012). |
| [21] | Khan, Y. and Austin, F. ‘‘Application of the Laplace decomposition method to nonlinear homogeneous and non-homogenous advection equations’’, Zeitschriftfür Naturforschung A, 65a, pp. 849–853 (2010). |
| [22] | Khan, Y. and Wu, Q. ‘‘Homotopy perturbation transform method for nonlinear equations using He’s polynomials’’, Computers & Mathematics with Applications, 61, pp. 1963–1967 (2011). |
| [23] | Zhou, J.K., Differential Transformation and its Application for Electrical Circuits, Huazhong University Press, Wuhan, China (in Chinese) (1986). |
| [24] | El-Shahed, M. ‘‘Application of differential transform method to non-linear oscillatory systems’’, Communications in Nonlinear Science and Numerical Simulation, 13, pp. 1714–1720 (2008). |
| [25] | Momani, S. and Ertürk, V.S. ‘‘Solutions of non-linear oscillators by the modified differential transform method’’, Computers & Mathematics with Applications, 55, pp. 833–842 (2008). |
| [26] | Yildirim, A., Gokdogan, A. and Merdan, M. ‘‘Chaotic systems via multistep differential transformation method’’, Canadian Journal of Physics, 90, pp. 391–406 (2012). |
| [27] | Mirzabeigy, A. and Yildirim, A. ‘‘Approximate periodic solution for nonlinear jerk equation as a third-order nonlinear equation via modified differential transform method’’, Engineering Computations, (2013). |
| [28] | Ertürk, V.S., Yildirim, A., Momani, S. and Khan, Y. ‘‘The differential transform method and Padé approximants for a fractional population growth model’’, International Journal of Numerical Methods for Heat & Fluid Flow, 22, pp. 791–802 (2012). |
| [29] | Nourazar, S., and A. Mirzabeigy. "Approximate solution for nonlinear Duffing oscillator with damping effect using the modified differential transform method." Scientia Iranica 20.2 (2013): 364-368. |



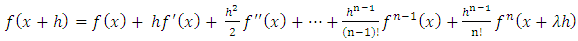
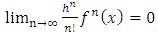
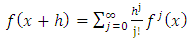
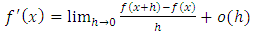
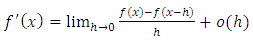
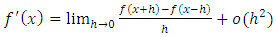
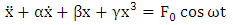
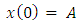
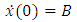
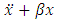 Simple harmonic oscillator with angular frequency
Simple harmonic oscillator with angular frequency 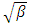 Small damping
Small damping 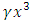 Small nonlinearity
Small nonlinearity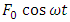 Small periodic forcing term with angular frequency
Small periodic forcing term with angular frequency 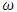 This is a forced oscillator with a nonlinear spring with a restoring force of
This is a forced oscillator with a nonlinear spring with a restoring force of 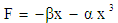 . Different values of α can create either a hardening spring (where α > 0) or a softening spring (where α < 0). Different values of β can also change the dynamics of the system. For values of β less than zero, the Duffing oscillator displays chaotic motion.
. Different values of α can create either a hardening spring (where α > 0) or a softening spring (where α < 0). Different values of β can also change the dynamics of the system. For values of β less than zero, the Duffing oscillator displays chaotic motion. 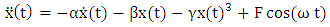
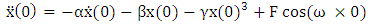
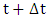 is obtained using Taylor expansion (1) up to the third term:
is obtained using Taylor expansion (1) up to the third term: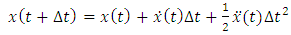
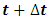 is obtained using the backward difference approximation of the first derivative (5):
is obtained using the backward difference approximation of the first derivative (5):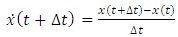
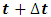 is obtained using equation (10) as:
is obtained using equation (10) as: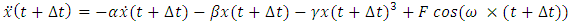
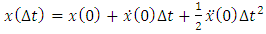
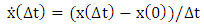
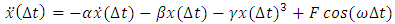
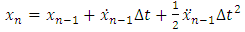
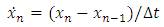
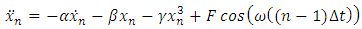
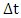 . The approximate velocity formula is modified to be obtained using the central difference approximation of the first derivative (6) as:
. The approximate velocity formula is modified to be obtained using the central difference approximation of the first derivative (6) as: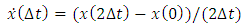
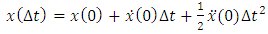
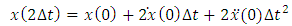
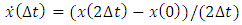
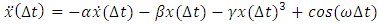
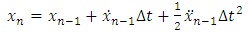
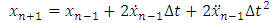
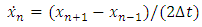
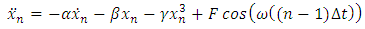
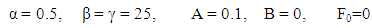
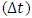 while in version 2 is of order
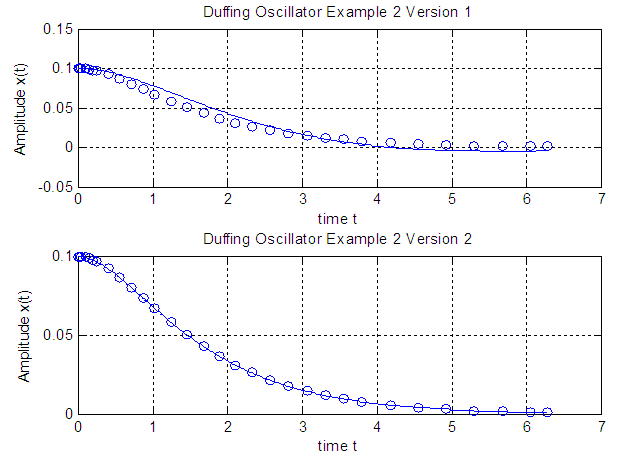
while in version 2 is of order 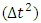 .Example 2
.Example 2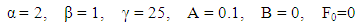
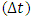 while in version 2 is of order
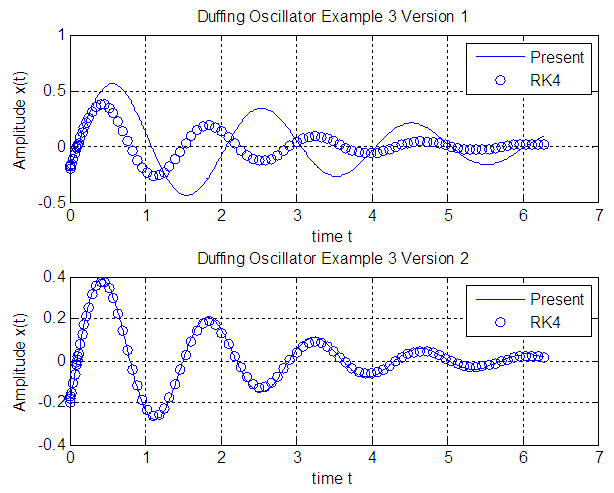
while in version 2 is of order 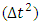 .Example 3
.Example 3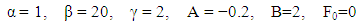
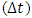 while in version 2 is of order
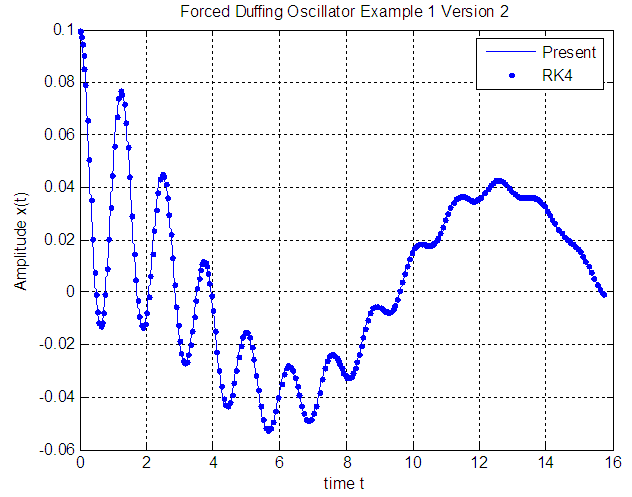
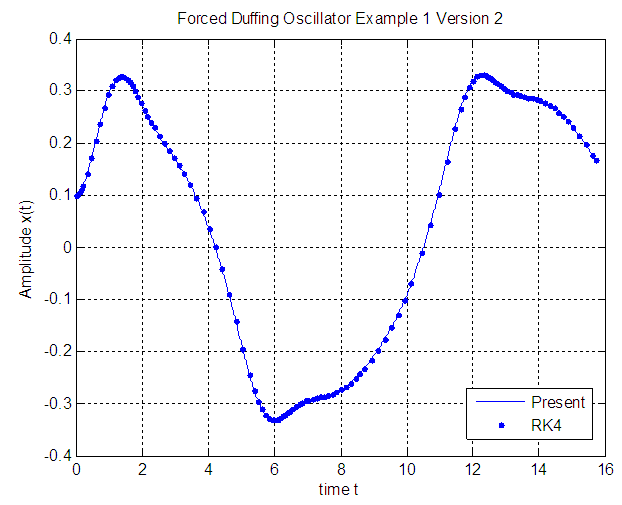
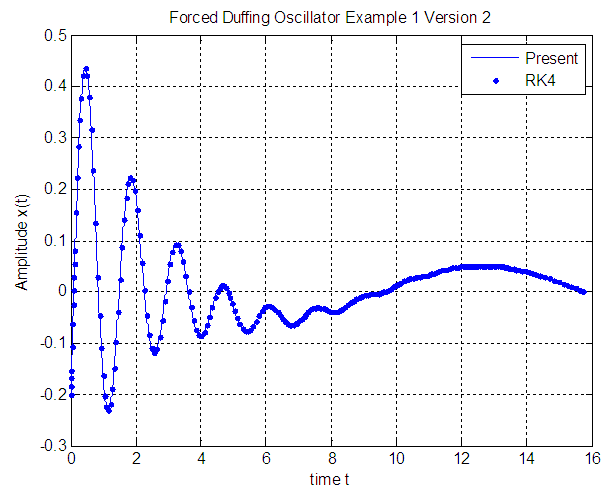
while in version 2 is of order 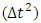 .As shown in Figures 1, 2, and 3 the results of the solution of the Duffing equation by the proposed technique has excellent agreement with that obtained by the Runge-Kutta 4thorder (RK4) method.
.As shown in Figures 1, 2, and 3 the results of the solution of the Duffing equation by the proposed technique has excellent agreement with that obtained by the Runge-Kutta 4thorder (RK4) method.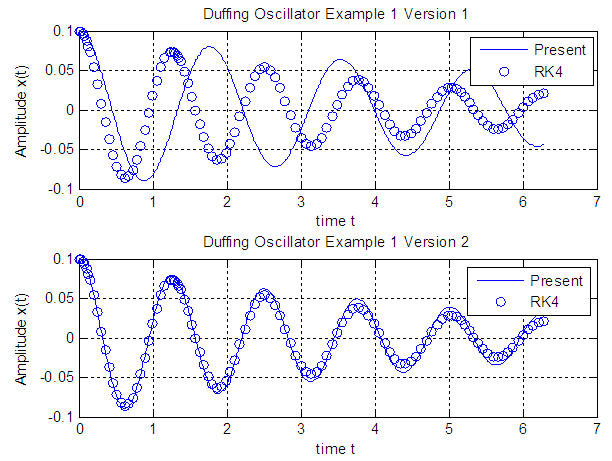
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML