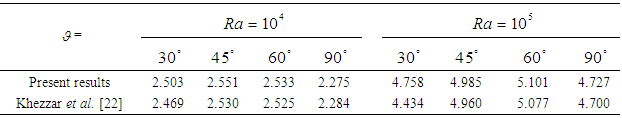-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2016; 6(3): 65-70
doi:10.5923/j.jmea.20160603.04

Natural Convection in Inclined Wavy-Wall Cavity Filled with Al2O3-water Nanofluid using Heatline Technique
Ching-Chang Cho, Ching-Huang Chiu, Kuo-Ching Chiu, Chong-You Lai
Department of Vehicle Engineering, National Formosa University, Taiwan
Correspondence to: Ching-Chang Cho, Department of Vehicle Engineering, National Formosa University, Taiwan.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This study uses the heatline technique to estimate the natural convection heat transfer characteristics in an inclined wavy-wall cavity filled with Al2O3-water nanofluid. In this study cavity, it is assumed that the left and right walls have a wavy surface and are maintained at a high and low temperature, respectively. In addition, the upper and lower walls are both flat and insulated. The flow and temperature fields within the cavity are governed by the continuity equation, momentum equations, energy equation and Boussinesq approximation, and are solved numerically using the finite-volume method and SIMPLE algorithm. The results show that the inclination angle of the cavity has no significant effect on the heat function contours and Nusselt number for low Rayleigh numbers. However, given high Rayleigh numbers, the effect of inclination angle on heat function contours and Nusselt number is significant. In addition, the results also show that the Nusselt number increases as the Al2O3 nanoparticles is added to the working fluid.
Keywords: Heatline, Nanofluid, Cavity, Wavy-wall, Natural convection
Cite this paper: Ching-Chang Cho, Ching-Huang Chiu, Kuo-Ching Chiu, Chong-You Lai, Natural Convection in Inclined Wavy-Wall Cavity Filled with Al2O3-water Nanofluid using Heatline Technique, Journal of Mechanical Engineering and Automation, Vol. 6 No. 3, 2016, pp. 65-70. doi: 10.5923/j.jmea.20160603.04.
Article Outline
1. Introduction
- Natural convection heat transfer in inclined cavities has many important applications in engineering systems, including solar energy collectors, double-glazed windows, car batteries, electronic cooling systems, crystal growth, and so on [1]. Thus, many researchers have investigated the flow field characteristics and heat transfer performance of natural convection in inclined cavities [2-4]. Overall, the results have shown that the flow conditions (e.g., Rayleigh number and Prandtl number) and geometry parameters (e.g., inclination angle and aspect ratio of cavity) have a significant effect on the flow characteristics and heat transfer behavior in the cavity. An optimal heat transfer performance occurs at a specific inclination angle of the cavity. In many engineering applications, wavy geometry structures are often used to enhance the heat transfer performance within cavities, such as heat exchangers, solar collectors, cooling systems for microelectronic devices, underground cable systems, and so forth. Many studies have shown that the use of the wavy geometry structures can improve the heat transfer performance when wavy geometry parameters have appropriate values [5-7].The heat transfer performance can also be improved by changing the thermophysical properties of the working fluid. Nanofluids, consisting of nanoparticles with high thermal conductivity (e.g., Al2O3 or Cu) suspended in a base fluid with low thermal conductivity (e.g., water or oil), provide an effective means of improving the thermophysical properties of the working fluid [8]. In recent years, many researchers have studied the problem of natural convection heat transfer in cavities filled with nanofluids [9-11]. Overall, the results have shown that the heat transfer performance increases with an increasing nanoparticle volume fraction. In addition, the type of nanoparticle added to the working fluid affects the heat transfer effect.To show the path of heat transfer, a useful tool is the heatline visualization technique [12, 13]. Many researchers have used the technique to study the natural convection heat transfer characteristics in cavities [14-16]. These results have shown that the use of the heatline visualization technique can show and explain the heat transfer process in detail.The present study investigates the natural convection heat transfer performance in an inclined wavy-wall cavity filled with Al2O3-water nanofluid using the heatline visualization technique. In modeling the cavity, the left and right walls are assumed to have a wavy surface and a high and low temperature, respectively, while the upper and lower walls are assumed to be flat and insulated. The flow behavior and heat transfer characteristics in the cavity are assumed to be governed by the continuity equation, momentum equations, energy equation and Boussinesq approximation. In performing the simulations, the governing equations are solved using the finite-volume method and the SIMPLE (semi-implicit method for pressure-linked equations) algorithm. The effects of the Rayleigh number, nanoparticle volume fraction and cavity inclination angle on the heat function distribution and Nusselt number in the inclined wavy-wall cavity filled with Al2O3-water are examined.
2. Mathematical Formulation
2.1. Governing Equations
- Figure 1 illustrates the studied cavity. As shown, the left and right walls have a wavy surface, while the top and bottom walls are flat. In addition, the width and height of this cavity are
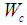 and
and  , respectively. Furthermore, the cavity is inclined at an angle
, respectively. Furthermore, the cavity is inclined at an angle 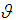 to the horizontal. The gravitational force
to the horizontal. The gravitational force  is assumed to act in the negative y-direction. It is assumed that the used nanofluid is Newtonian and incompressible. The fluid flow in the cavity is assumed to be two-dimensional, laminar and steady state. In addition, the base fluid and nanoparticles are in thermal equilibrium and no relative motion occurs between them. Furthermore, the thermophysical properties of the nanofluid are all constant other than the density which varies in accordance with the Boussinesq approximation. Let the following non-dimensional quantities be introduced:
is assumed to act in the negative y-direction. It is assumed that the used nanofluid is Newtonian and incompressible. The fluid flow in the cavity is assumed to be two-dimensional, laminar and steady state. In addition, the base fluid and nanoparticles are in thermal equilibrium and no relative motion occurs between them. Furthermore, the thermophysical properties of the nanofluid are all constant other than the density which varies in accordance with the Boussinesq approximation. Let the following non-dimensional quantities be introduced: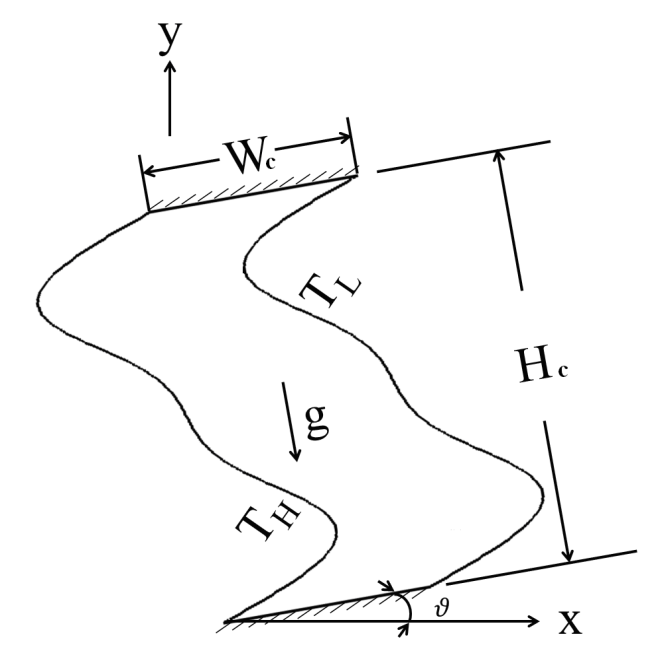 | Figure 1. Schematic illustration of wavy wall cavity |
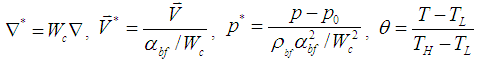 | (1) |
 is the velocity vector with components
is the velocity vector with components 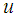 and
and 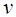 in the x- and y-directions, respectively;
in the x- and y-directions, respectively; 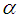 is the thermal diffusivity;
is the thermal diffusivity; 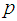 is the pressure;
is the pressure; 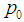 is the reference pressure;
is the reference pressure; 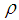 is the density;
is the density; 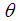 is the dimensionless temperature;
is the dimensionless temperature; 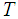 is the temperature;
is the temperature; 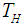 and
and 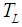 are the high temperature and low temperature, respectively; and the subscript
are the high temperature and low temperature, respectively; and the subscript 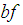 indicates the base fluid (i.e., water). Under the conditions of ignoring thermal radiation and viscous dissipation effects, the governing equations described the flow and temperature fields have the following non-dimensionalized forms:
indicates the base fluid (i.e., water). Under the conditions of ignoring thermal radiation and viscous dissipation effects, the governing equations described the flow and temperature fields have the following non-dimensionalized forms: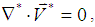 | (2) |
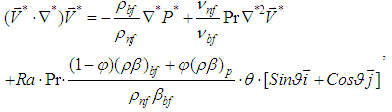 | (3) |
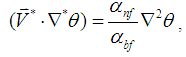 | (4) |
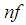 and
and 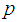 denote the nanofluid and nanoparticles, respectively;
denote the nanofluid and nanoparticles, respectively; 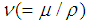 is the kinematic viscosity;
is the kinematic viscosity; 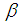 is the thermal expansion coefficient;
is the thermal expansion coefficient; 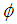 is the volume fraction of Al2O3 nanoparticles;
is the volume fraction of Al2O3 nanoparticles; 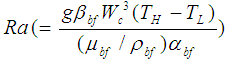 is the Rayleigh number; and
is the Rayleigh number; and 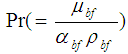 is the Prandtl number. In addition, the effective thermophysical properties of nanofluid presented in Eqs. (2)-(4) can be estimated as follows [17, 18]: density,
is the Prandtl number. In addition, the effective thermophysical properties of nanofluid presented in Eqs. (2)-(4) can be estimated as follows [17, 18]: density, 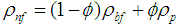 ; viscosity,
; viscosity, 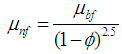 ; thermal diffusivity,
; thermal diffusivity, 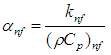 ; thermal conductivity,
; thermal conductivity, 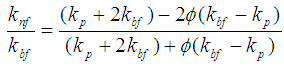 ; and specific heat,
; and specific heat, 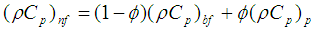 . Furthermore, the Nusselt number (Nu) estimated the heat transfer performance can be defined in the non-dimensionalized form:
. Furthermore, the Nusselt number (Nu) estimated the heat transfer performance can be defined in the non-dimensionalized form: 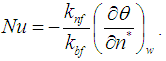 | (5) |
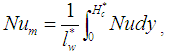 | (6) |
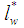 is the non-dimensional length of the wavy-wall.
is the non-dimensional length of the wavy-wall.2.2. Boundary Conditions
- As shown in Fig. 1, the left wall of the cavity is maintained at a constant high temperature, the right wall has a constant low temperature, and the top and bottom walls are both insulated. A no-slip impermeable velocity boundary condition is assumed to apply at all of the wall surfaces. The dimensionless boundary conditions can be summarized as follows:
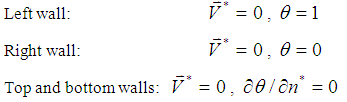
2.3. Heat Function
- The energy equation in a two-dimensional, incompressible, and steady-state for nanofluid-filled cavity without heat generation can be written in the following non-dimensionalized form [12, 13]:
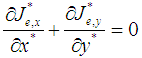 | (7) |
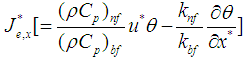 and
and 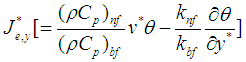 are the heat flux vector in x- and y- directions, respectively. Let the dimensionless heat function
are the heat flux vector in x- and y- directions, respectively. Let the dimensionless heat function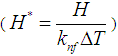 be defined as follows:
be defined as follows: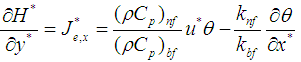 | (8a) |
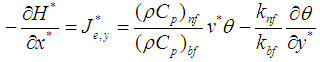 | (8b) |
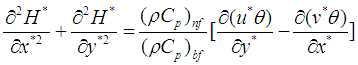 | (9) |
2.4. Wavy-Wall Geometry and Numerical Solution Procedure
- The non-dimensional profile of the wavy-wall was modeled as follows:
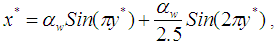 | (10) |
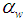 is the wave amplitude. The grid system of the wavy-wall cavity was generated by solving a set of Poisson equations [20]. A generalized coordinate transform technique was used to transform the governing equations from a Cartesian coordinate system to a generalized curvilinear coordinate system. The transformed governing equations have following generalized form [17-19]:
is the wave amplitude. The grid system of the wavy-wall cavity was generated by solving a set of Poisson equations [20]. A generalized coordinate transform technique was used to transform the governing equations from a Cartesian coordinate system to a generalized curvilinear coordinate system. The transformed governing equations have following generalized form [17-19]: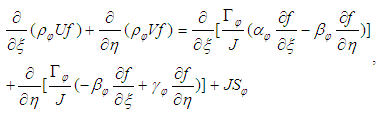 | (11) |
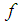 is a generalized variable. The finite-volume method [21] is used to discretize the governing equations and corresponding boundary conditions. The second-order upwind scheme is utilized to discretize the convection terms in the Eqs. (3) and (4). The SIMPLE algorithm [21] is used to couple the velocity-pressure fields. Finally, line-by-line TDMA (tri-diagonal matrix algorithm) iterative scheme is imposed to solve the discretized algebraic equations.
is a generalized variable. The finite-volume method [21] is used to discretize the governing equations and corresponding boundary conditions. The second-order upwind scheme is utilized to discretize the convection terms in the Eqs. (3) and (4). The SIMPLE algorithm [21] is used to couple the velocity-pressure fields. Finally, line-by-line TDMA (tri-diagonal matrix algorithm) iterative scheme is imposed to solve the discretized algebraic equations.2.5. Grid-Independence Evaluation and Numerical Validation
- The variations of the mean Nusselt number along the hot wavy-wall surface with the grid sizes of
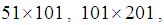
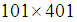 and
and 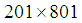 are performed in the cavity with
are performed in the cavity with 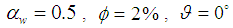 and
and 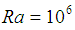 . The obtained results have shown that a grid size of
. The obtained results have shown that a grid size of 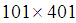 has a grid-independent solution. The computational domain was thus meshed accordingly.The present numerical results for the variation of the mean Nusselt number in an inclined square cavity with Pr = 100 have compared with those presented in [22]. Note that in the compared cavity, the top and bottom walls were maintained at low and high temperatures, respectively, while the left and right walls were assumed to be insulated. Table 1 presents the results. As shown, it is seen that the present results are consistent with those presented in [22].
has a grid-independent solution. The computational domain was thus meshed accordingly.The present numerical results for the variation of the mean Nusselt number in an inclined square cavity with Pr = 100 have compared with those presented in [22]. Note that in the compared cavity, the top and bottom walls were maintained at low and high temperatures, respectively, while the left and right walls were assumed to be insulated. Table 1 presents the results. As shown, it is seen that the present results are consistent with those presented in [22].
|
3. Results and Discussion
- In the current study, the Al2O3-water nanofluid is used. The thermophysical properties of the Al2O3 nanoparticles are as follows [17-19]:
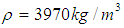 ,
, 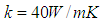 ,
, 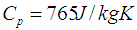 , and
, and 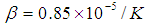 . The thermophysical properties of the water are as follows:
. The thermophysical properties of the water are as follows: 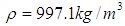 ,
, 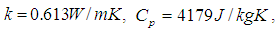 and
and 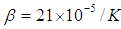 . In addition, the Prandtl number was set as
. In addition, the Prandtl number was set as 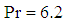 . The amplitude of the wavy surface is given
. The amplitude of the wavy surface is given 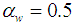 . Figures 2 and 3 plot the heat function contours in the cavity given Rayleigh numbers of
. Figures 2 and 3 plot the heat function contours in the cavity given Rayleigh numbers of 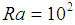 and
and 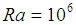 , respectively. Given a low Rayleigh number, since the flow velocity due to buoyancy force in the cavity is lower, the heat energy is transported slowly and more uniformly form the high temperature wall to low temperature wall for all considered nanoparticle volume fractions and inclination angles. As a result, a more uniform heat function contours without enclosed cell are presented in the cavity (see Fig. 2). Given a high Rayleigh number, since the flow velocity is high, the heat energy can be transported fast via the fluid flow for all considered nanoparticle volume fractions and inclination angles. Consequently, the heat function contours are more complex. It also shows that enclosed cells are presented in the cavity. This result indicates that the heat energy is rotated in the enclosed cells. Comparing the heat function contours between the two Rayleigh numbers, it is shown that higher values of heat function are presented in the case of the higher Rayleigh number. This result implies that the heat transfer is better in the case of the higher Rayleigh number. When the cavity is inclined, the direction of the gravitational force acting on the nanofluid changes, and prompts a corresponding change in the buoyancy effect. At low Rayleigh numbers, since the buoyancy effect is weak and the fluid flow is slow, there is no significant change in the heat function patterns. However, at high Rayleigh numbers, the buoyancy effect is strong and is thus susceptible to changes in the orientation of the cavity. Therefore, significant changes in the distribution of heat function contours occur as the inclination angle is varied.
, respectively. Given a low Rayleigh number, since the flow velocity due to buoyancy force in the cavity is lower, the heat energy is transported slowly and more uniformly form the high temperature wall to low temperature wall for all considered nanoparticle volume fractions and inclination angles. As a result, a more uniform heat function contours without enclosed cell are presented in the cavity (see Fig. 2). Given a high Rayleigh number, since the flow velocity is high, the heat energy can be transported fast via the fluid flow for all considered nanoparticle volume fractions and inclination angles. Consequently, the heat function contours are more complex. It also shows that enclosed cells are presented in the cavity. This result indicates that the heat energy is rotated in the enclosed cells. Comparing the heat function contours between the two Rayleigh numbers, it is shown that higher values of heat function are presented in the case of the higher Rayleigh number. This result implies that the heat transfer is better in the case of the higher Rayleigh number. When the cavity is inclined, the direction of the gravitational force acting on the nanofluid changes, and prompts a corresponding change in the buoyancy effect. At low Rayleigh numbers, since the buoyancy effect is weak and the fluid flow is slow, there is no significant change in the heat function patterns. However, at high Rayleigh numbers, the buoyancy effect is strong and is thus susceptible to changes in the orientation of the cavity. Therefore, significant changes in the distribution of heat function contours occur as the inclination angle is varied.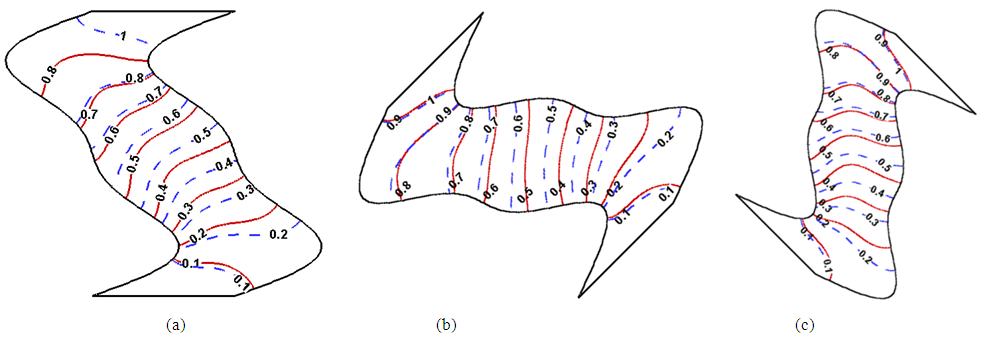 | Figure 2. Distribution of heatlines in cavity given Rayleigh numbers of 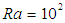 and inclination angles of: (a) and inclination angles of: (a) 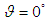 , (b) , (b) 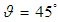 , and (c) , and (c) 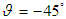 . Note that solid line indicates . Note that solid line indicates 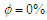 , and dashed line indicates , and dashed line indicates  |
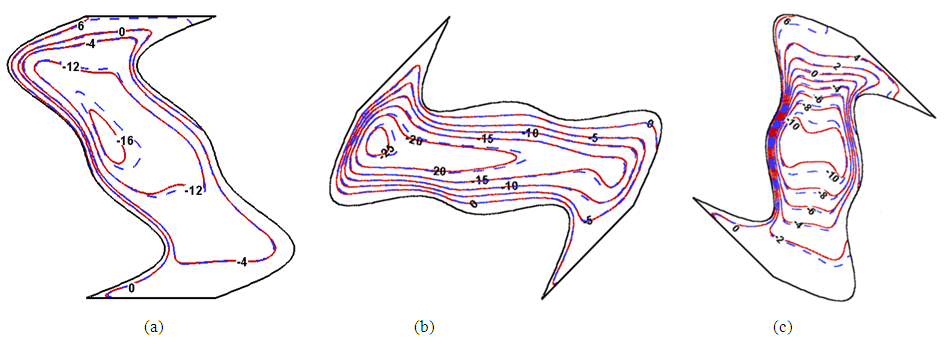 | Figure 3. Distribution of heatlines in cavity given Rayleigh numbers of 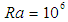 and inclination angles of: (a) and inclination angles of: (a) 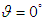 , (b) , (b) 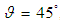 , and (c) , and (c) 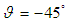 . Note that solid line indicates . Note that solid line indicates 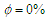 , and dashed line indicates , and dashed line indicates 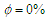 |
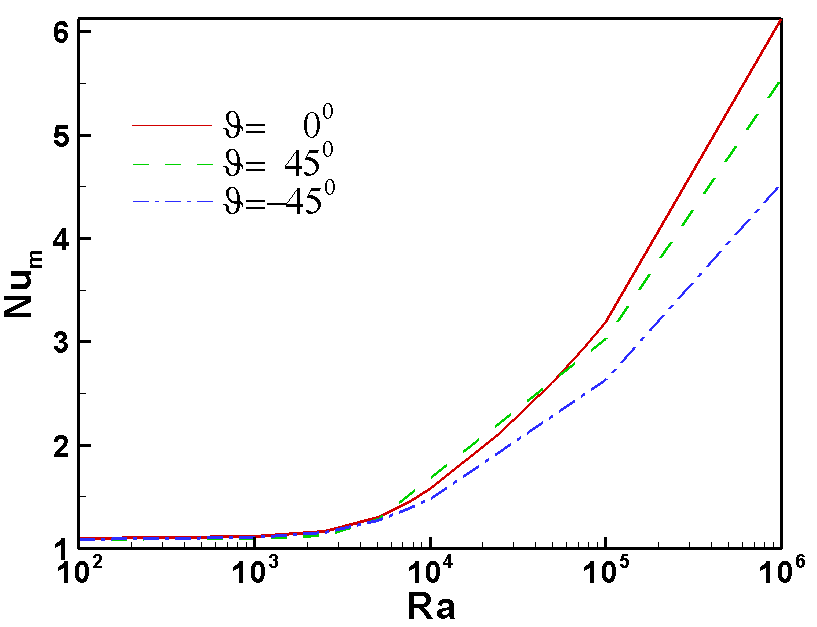 | Figure 4. Variation of mean Nusselt number with Rayleigh number as function of inclination angle. Note that 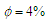 |
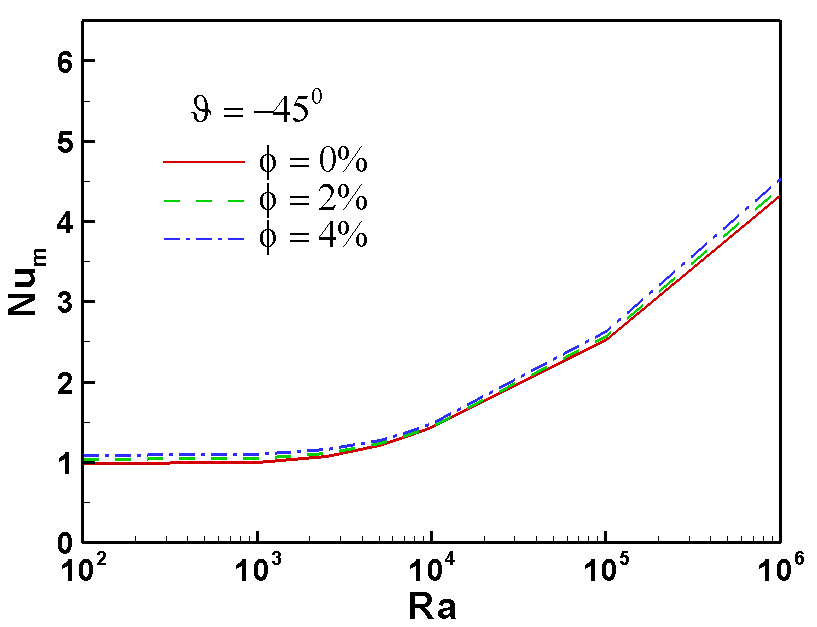 | Figure 5. Variation of mean Nusselt number with Rayleigh number as function of nanoparticle volume fraction. Note that 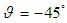 |
4. Conclusions
- This study has used the heatline technique to estimate the natural convection heat transfer performance of Al2O3-water nanofluid in a cavity bounded by vertical isothermal walls with a wavy surface and straight upper and lower walls with adiabatic conditions. In performing the simulations, the governing equations have been modeled using the continuity equation, momentum equations, energy equation and Boussinesq approximation, and then solved numerically using the finite volume method and SIMPLE algorithm. The results have shown that the distribution of heat function in the cavity is strongly dependent on the inclination angle of the cavity for higher Rayleigh numbers. However, given low Rayleigh numbers, the inclination angle has no significant effect on heat function contours and Nusselt number. In addition, the results have also shown that the use of nanofluid can increase the Nusselt number.
ACKNOWLEDGEMENTS
- The authors would like to thank the Ministry of Science and Technology, Taiwan, R.O.C. for the financial support of this study under Contract No. MOST 104-2221-E-150-045.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML