Daiki Goto, Agus Santoso, Tomoaki Takehira, Ahmad Aslam, Akimaro Kawahara, Michio Sadatomi
Graduate School of Science and Technology, Kumamoto University, Japan
Correspondence to: Daiki Goto, Graduate School of Science and Technology, Kumamoto University, Japan.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Experimental investigations were conducted for gas–liquid two-phase flow through sudden expansion in horizontal rectangular mini-channel. The cross-sectional dimensions of the channel with the height (H), the width (W) and the hydraulic diameter (DH) for the narrow channel are 2.79 mm, 3.09 mm and 2.94 mm, while those for the wide channel are 2.95 mm, 5.98 mm and 3.95 mm. In order to know the effects of liquid properties, water and viscoelastic liquid, namely 0.4 wt % polyacrylamide (PAM) aqueous solution are selected as the working liquids, while air as the working gas. The local pressures upstream and downstream from the expansion were measured with calibrated pressure sensors, and the pressure distribution map was drawn to determine the frictional pressure drop in the test channel and the pressure change at the expansion for single-phase and two phase flows. The pressure change data at the expansion for two-phase flows were compared with the calculations by several correlations in some literatures. These are reported in the present paper.
Keywords:
Rectangular mini-channel, Two-phase flow, Sudden expansion, Non-Newtonian fluid
Cite this paper: Daiki Goto, Agus Santoso, Tomoaki Takehira, Ahmad Aslam, Akimaro Kawahara, Michio Sadatomi, Pressure Drop for Gas and Non-Newtonian Liquid Two-Phase Flows across Sudden Expansion in Horizontal Rectangular Mini-Channel, Journal of Mechanical Engineering and Automation, Vol. 6 No. 3, 2016, pp. 51-57. doi: 10.5923/j.jmea.20160603.02.
1. Background
The flow channel normally involves several geometrical singularities such as abrupt area changes (sudden expansion, sudden contraction, valve or orifice). The flow of two-phase mixtures across sudden expansions and contractions is commonly seen among piping connections as well as relevant to many applications such as chemical reactors, power generation units, oil wells and petrochemical plants (Wang et al., 2010). In particular, the small and narrow channels are widely adopted in compact heat exchangers (Chen et al., 2009). One of the simplest arrangements for the heat removal is using the liquid flow and convective heat transfer with or without phase change in small rectangular channels (Chen et al., 2007). Recently, such a flow through singularity in micro and mini-channels of 100 μm to 10 mm becomes popular because compact heat exchangers with phase change, such as cooling devices of electronic equipment and refrigerators, are miniaturized (Sadatomi et al, 2013). Therefore, the understanding of the characteristics on two phase flow through the singularities in mini-channel is essential for designing and developing such small scale devices. Regarding gas-liquid two-phase flows through a sudden expansion in mini-channels, several studies have been reported. Abdelall et al. (2005) performed an experimental study of pressure drop caused by abrupt flow area changes in small circular channels. The larger and smaller tube diameters were 1.6 and 0.84 mm, respectively. Deionized water and air were used as two-phase working fluids. Chen et al. (2008) conducted experimental investigation of the two-phase flow characteristics across sudden expansion using air and water. The expansion test section was from small rectangular channels (3 by 6 mm and 3 by 9 mm in short and long sides) into a small circular tube (3 mm in diameter). Sadatomi et al. (2013) investigated air-water two-phase flow through a sudden expansion in a horizontal rectangular mini-channel with 3.03 mm by 3.02 mm and 5.97 mm by 3.09 mm in the width and the height. The two-phase pressure drop at the expansion was the best predicted by Wadle’s correlation (1989).From the above discussion, it is cleared that most studies have been conducted based on the Newtonian fluid data as the test liquid, and there are a few data using non-Newtonian liquids, seen in chemical reactor and bio reactor etc. (Böhm et al., 2014). In this connection, the aim of this study is to investigate experimentally the effects of non-Newtonian liquid on the pressure change at a sudden expansion. Adiabatic experiments were conducted to obtain such data for gas-liquid two phase flows through a sudden expansion in a horizontal rectangular mini-channel. The cross-sectional sizes of the channel were 3.09mm by 2.79 mm and 5.98 mm by 2.95 mm. The corresponding area ratio was σA = 0.49. In order to study the effects of non-Newtonian properties, water and aqueous solution of polyacrylamide (PAM), which exhibits pseudo plastic with viscoelasticity, were used as the test liquid, while air as the test gas. The present pressure change data obtained from air-water and air-PAM system are compared with calculation by correlations in literatures. Results of the experiments and the comparison are described in this paper.
2. Experimental Methods
2.1. Test Apparatus
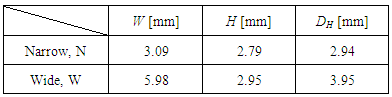
Figure 1 shows a schematic diagram of the test channel with a sudden expansion placed on a horizontal plane. The test channel is rectangular in cross-section and is made of transparent acrylic resin for visual observation. Table 1 shows the cross-sectional dimensions of test channel with the width (W), the height (H) and the hydraulic diameter (DH): They are 3.09 mm, 2.79 mm and 2.94 mm for the narrow channel, while 5.98 mm, 2.95 mm and 3.95 mm for the wide channel, thus the area ratio σA is about 0.49.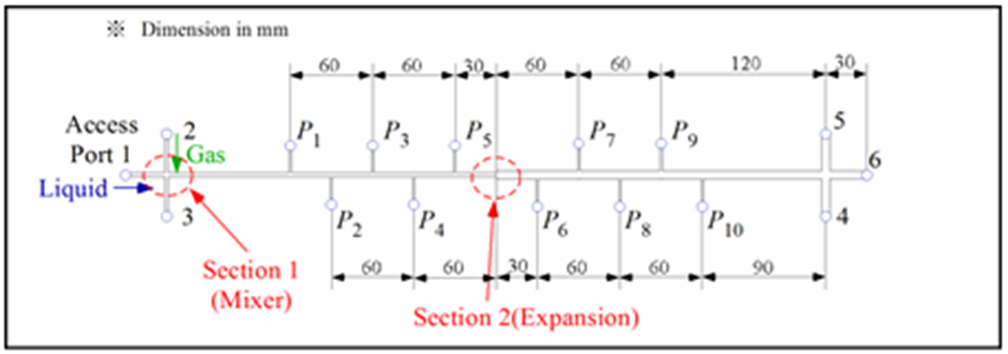 | Figure 1. Test channel with sudden expansion |
Table 1. Dimensions of test channel cross section
 |
| |
|
The ports #1 and #2 in Fig. 1 were the liquid and the gas inlet ports. Therefore, two phases were supplied through a T-junction type gas-liquid mixer. The port #6 was the outlet of the gas-liquid mixture to atmosphere. The ports #3, #4 and #5 were closed in the present experiment. It is noted that if ports #5 and #6 were used as the inlet ports of gas and liquid, and ports #4, #2 and#3 were closed, the sudden contraction test can be conducted with the same test channel. P1 to P12 are the pressure taps, and the pressure at P4 was measured with a gauge type pressure transducer (Yokogawa, FP101-L31-L20). The pressures at other pressure taps were determined from the difference in pressure between the respective taps and P4 tap measured with a differential pressure transducer (Validyne, DP15-32 and DP15-26 depending on the pressure range). The accuracy of the pressure measurement was confirmed within 3.5 Pa from a calibration test. Volume flow rate of air was measured with a flow meter (KEYENCE, FD-A10 and FD-A1 depending on the flow rate range) with accuracy of 3%, while that of liquids with a flow meter (KEYENCE, FD-S) with accuracy of 2%. In order to obtain accurate time averaged values of air and water flow rates and pressures, the output signals from the respective sensors were fed to a personal computer via A/D converter at nominally 2 kHz over 20 sec.In this study, tap water and aqueous solution of 0.4 wt % polyacrylamide (PAM) are selected as the test liquid, while air at room temperature as the test gas. PAM aqueous solution is known as a kind of non-Newtonian fluid having viscoelasticity (Chhabra et al., 1984). Also, PAM aqueous solution has shear thinning effect where the fluid’s viscosity decreases with increasing of shear rate and is often expressed by the Ostwald-de Waele power law model as follows: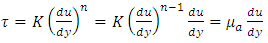 | (1) |
where 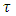 is the shear stress,
is the shear stress, 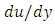 the shear rate, K the consistency coefficient, n the flow index and
the shear rate, K the consistency coefficient, n the flow index and 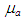
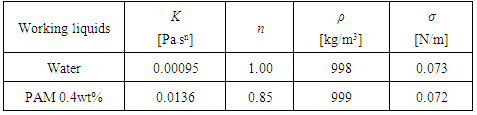
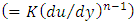 the apparent viscosity. In this study, the values of K and n for each test liquids were determined with a capillary method (Farooqi et al., 1980), and are listed in Table 2 together with the density and the surface tension. n for both water and PAM aqueous solution are investigated within the share rate range of 80 to 12000 1/s. In addition, the density and the surface tension are nearly the same between water and PAM aqueous solution. So, any changes in the test results are due mainly to the change in the viscosity of the test liquid.
the apparent viscosity. In this study, the values of K and n for each test liquids were determined with a capillary method (Farooqi et al., 1980), and are listed in Table 2 together with the density and the surface tension. n for both water and PAM aqueous solution are investigated within the share rate range of 80 to 12000 1/s. In addition, the density and the surface tension are nearly the same between water and PAM aqueous solution. So, any changes in the test results are due mainly to the change in the viscosity of the test liquid. Table 2. Physical properties of test liquids
 |
| |
|
For single-phase flow experiments, the ranges of the mean velocity u were changed from 0.1 to 2 m/s in the narrow channel for both test liquids. For two-phase flow experiments, the volumetric fluxes of liquid and gas were changed as jL = 0.5, 1 m/s and jG = 0.1, 0.5, 1, 5, 10 m/s for both test liquids. The fluid temperature was 20 to 25ºC.
2.2. Data Reduction for Pressure Change at Expansion
Figures 4 (a) and (b) show examples of the pressure distribution data obtained for air-water and air-PAM aqueous solution two-phase flows at jG = 0.1 m/s and jL = 0.5 m/s. The ordinate is the gauge pressure, while the abscissa is the distance from the expansion. The total pressure change across sudden expansion, ∆Pe, was determined by the extrapolations of the axial pressure profiles upstream and downstream from the expansion. ∆Pe consists of the reversible pressure rise, ∆Pe,R, and irreversible pressure drop, ∆Pe,I as shown by pattern diagram in Fig. 2 (a). | Figure 2. Pressure distribution along upstream and downstream from expansion |
3. Results and Discussions
3.1. Single-phase Friction Factor
In order to check the accuracy of the pressure measurement, the single-phase friction factors were determined from the fully developed upstream and the downstream pressure gradients. Figs. 3 (a) and (b) show the Darcy friction factor data respectively for the channels upstream and downstream of the expansion. The data of water are plotted against the Reynolds number (=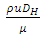 , where µ is the viscosity, u is the mean velocity). On the other hand, in the case of PAM aqueous solution, the generalized Reynolds number (Kozicki et al., 1966) was used to consider non-Newtonian properties, and this is given by:
, where µ is the viscosity, u is the mean velocity). On the other hand, in the case of PAM aqueous solution, the generalized Reynolds number (Kozicki et al., 1966) was used to consider non-Newtonian properties, and this is given by: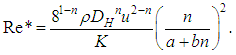 | (2) |
Here, a and b are constants depending on the cross-sectional shape of the channel. In the present case, a = 0.213 and b = 0.677 for the narrow channel, while a = 0.242 and b = 0.725 for the wide channel. The present data in laminar flow region are compared with calculated curve by Shah and London (1978) which is a function of aspect ratio, 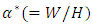 , for a rectangular channel:
, for a rectangular channel: 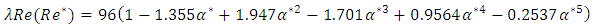 | (3) |
In addition, the data in turbulent flow are compared with calculated line by Sadatomi et al. (1982). As seen in Fig. 3, most data for water approached to such calculated lines. In the case of PAM, the data in laminar flow also approached to the lines by use of the generalized Reynolds number, however, in present experimental condition, the data in turbulent flow were not observed because of high viscosity of PAM.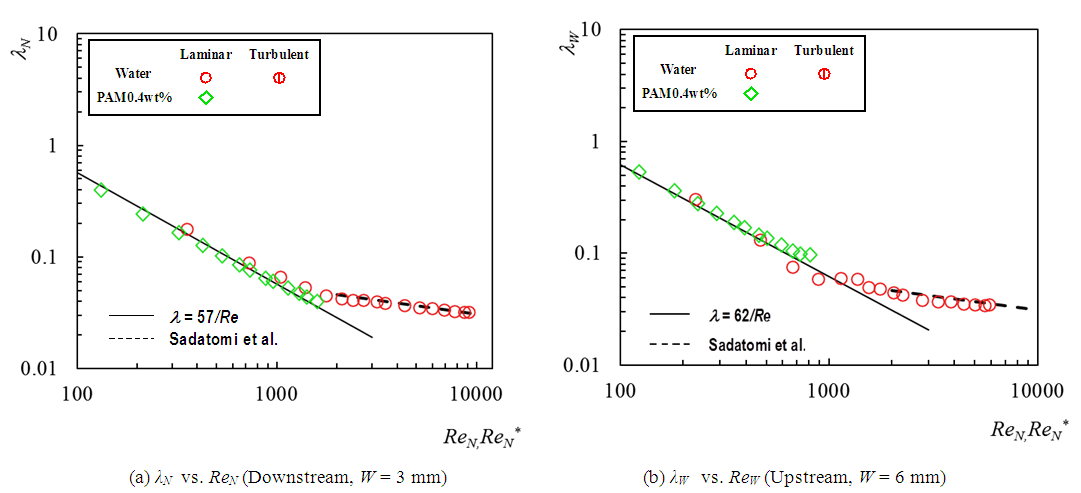 | Figure 3. Single-phase friction factors in channels upstream and downstream from the expansion |
3.2. Single-phase Pressure Change at Expansion
The data of single-phase pressure change at expansion, ∆Pe, are plotted in Fig. 4. ∆Pe for both the water flow and the PAM flow increase with the mean velocity of liquid in narrow channel, uN. This is caused by the increase in the ratio of reversible pressure rise, ∆Pe,R, against irreversible pressure drop, ∆Pe,I. In the case of PAM, for PAM ∆Pe were higher than that of water. From this results, it is found that ∆Pe,I for PAM is smaller than water.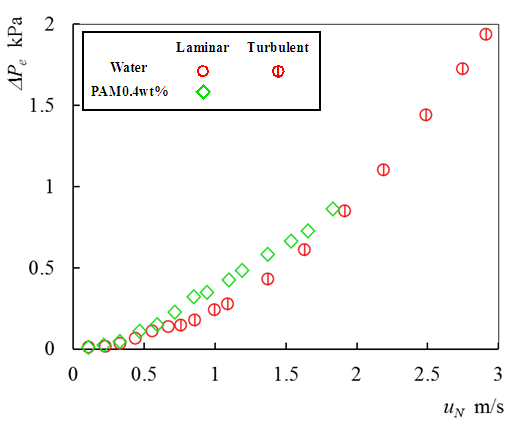 | Figure 4. Single-phase pressure change at expansion |
3.3. Expansion Pressure Loss for Single-phase Flow
By substituting ∆Pe data into the following equations, we determined the experimental value of an expansion pressure loss coefficient for single-phase liquid flow, ke: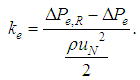 | (4) |
Here,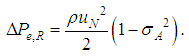 | (5) |
The resulting ke values are plotted in Fig. 5. In addition, broken line shows the calculation by Borda-Carnot’s fomula 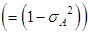 . As seen in this figure, the ke data gradually approach the calculation line with the increase in ReN or ReN*, and the water data in turbulent flow become almost constant and nearby the calculation line. The PAM data also approach the calculation line though no data was obtained in turbulent flow region.
. As seen in this figure, the ke data gradually approach the calculation line with the increase in ReN or ReN*, and the water data in turbulent flow become almost constant and nearby the calculation line. The PAM data also approach the calculation line though no data was obtained in turbulent flow region.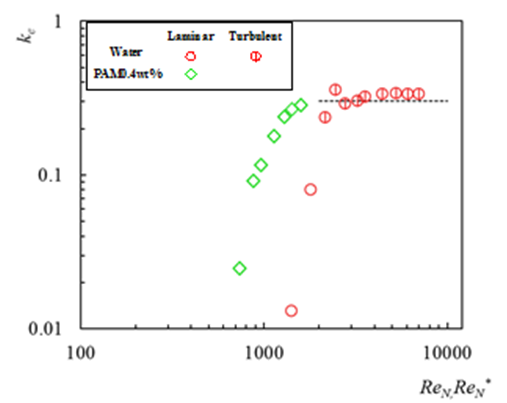 | Figure 5. Expansion loss for single phase flow |
3.4. Flow Pattern
Figure 6 shows typical upside view of flows downstream of the expansion for air-water and air-PAM flow in the wide channel. Three types of flow pattern, (a) a bubbly flow, (b) a slug flow and (c) an annular flow, were observed for both air-water and air-PAM flows under the present flow conditions. In the bubbly flow, bubble size is smaller for air-PAM flow than air-water flow. In addition, the bubbles tend to drift to right or left side wall of the wide channel. This drift is not due to the gravity effect because the gravity direction is perpendicular to the paper. For the slug flows of both air-water and air-PAM flows, the bubble length becomes longer than that for the bubbly flow. The bubble length is longer for air-PAM flow than air-water one, and the bubble nose become sharper for air-PAM flow. Furthermore, liquid film thickness around the gas bubble is thicker for air-PAM flow than air-water flow. For the annular flow, the liquid flow as liquid film on the channel wall, and gas flow in core of the channel. The liquid film thickness is thicker for air-PAM flow than air-water flow. The thicker liquid film for the slug and annular flows might be caused by higher viscosity of PAM solution.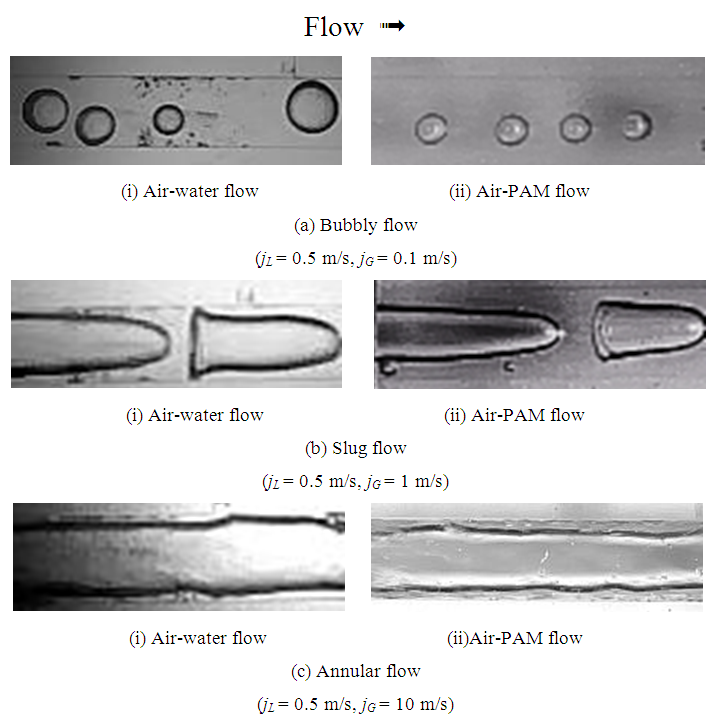 | Figure 6. Typical flow in the test channel |
3.5. Two-phase Pressure Change at Expansion
The data on the two-phase pressure change at expansion, ∆Pe, are plotted against the gas volumetric flux, jG in Fig. 7. The data points are marked with different symbols depending on the test liquid and the liquid volumetric flux, jL. In the case of water, at both jL = 0.5 and 1 m/s, ∆Pe increased with increasing of jG. This indicates that the effect of the expansion on reversible pressure rise becomes profound due to the increase in mean liquid velocity caused by the increase in void fraction. ∆Pe were higher for PAM than water when jG is low. This result means that the ratio of irreversible pressure drop to reversible pressure rise for PAM become smaller than that for water, that is, the effect of the expansion on flow disturbance is significant at low jG.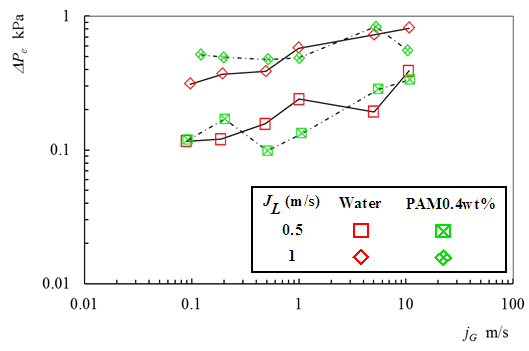 | Figure 7. Two-phase flow pressure change at expansion |
3.6. Validation Test of Correlation for Two-phase ∆Pe
In order to find better correlation for predicting two-phase pressure change at expansion, the present ∆Pe data was compared with five prediction model/correlations proposed for gas and Newtonian liquid two-phase flow. Table 3 lists the root mean square values of absolute error, ∆Pe,cal -∆Pe,exp, respectively for the air-water flows, the air-PAM flows and all the flows. Table 3. RMS errors in ∆Pe prediction
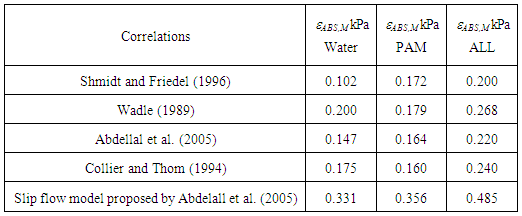 |
| |
|
Figures 8 (a) - (e) compare the two-phase pressure change between experiment and calculations. Four correlations except for a slip flow model proposed by Abdelall et al. (2005) predict well the present data, although the correlations by Wadle (1989), Abdelall et al. (2005) and Collier and Thom (1994) tend to under-predict the data. Among these correlations, the following Shmidt and Friedel’s correlation gave the best prediction. 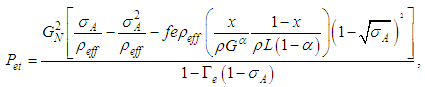 | (6) |
where,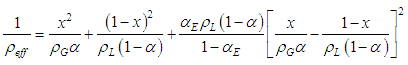 | (7) |
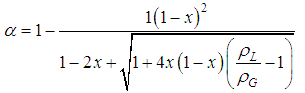 | (8) |
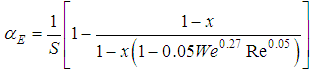 | (9) |
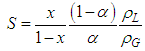 | (10) |
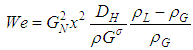 | (11) |
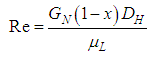 | (12) |
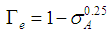 | (13) |
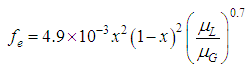 | (14) |
In these equations, the subscripts L, G means liquid and gas, respectively. x is the quality, GN the total mass flux in narrow channel, 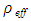 the effictive dencity in two-phase mixture,
the effictive dencity in two-phase mixture, 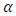 the void fraction. In addition,
the void fraction. In addition, 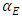 the mean volumetric entrainment, S are the slip ratio, We the Weber number, and
the mean volumetric entrainment, S are the slip ratio, We the Weber number, and 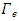 the base pressure coefficient, fe the friction factor in expansion.In the present calculation, non-Newtonian properties are taken into account by replacing
the base pressure coefficient, fe the friction factor in expansion.In the present calculation, non-Newtonian properties are taken into account by replacing 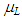 by apparent viscosity
by apparent viscosity 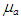 :
: 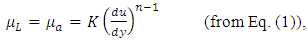 | (15) |
In addition, the share rate was approximated to the next value (Farooqi et al., 1980):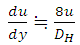 | (20) |
The reason of the best prediction by Schidt and Friedel’s correlation might be that the correlation can account for the liquid properties by Eqs. (12) and (14), while other four correlations do not consider the viscosity effects.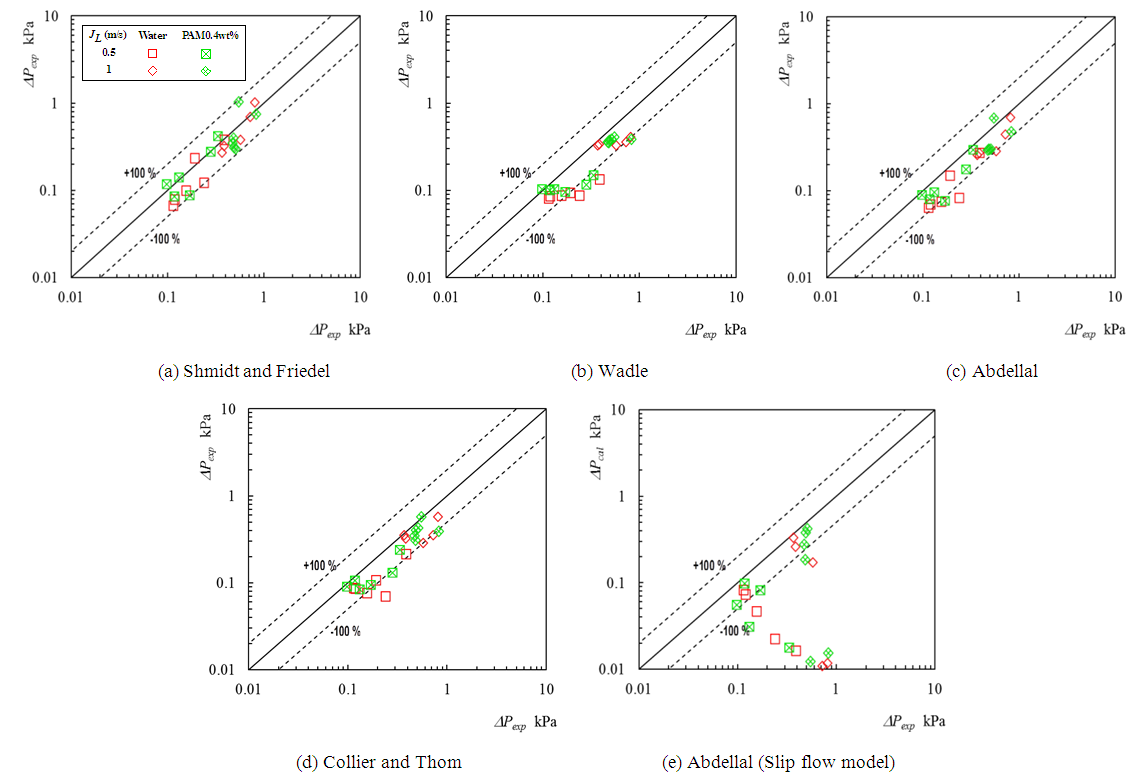 | Figure 8. Comparison of present data by correlations |
4. Conclusions
Liquid single-phase flow and air non-Newtonian liquid two-phase flow experiments were conducted at room temperature and at near atmospheric pressure using a horizontal rectangular mini-channel with a sudden expansion. The width and the height of the channel were from 3 mm by 3 mm to 6 mm by 3 mm. In order to study the effects of liquid viscosity, water and polyacrylamide (PAM) aqueous solution with mass concentration of 0.4wt% were used as the test liquid. From the present investigation, the conclusions can be summarized as follows:1. Single-phase friction factor data for water agreed with theoretical values in both laminar and turbulent flow, while the data for the PAM in laminar flow also agreed with the values by using the generalized Reynolds number.2. Pressure change across the sudden expansion in single- phase flow for both the water flow and the PAM flow increased with the mean velocity in narrow channel. The pressure change for the PAM was larger than water. This results indicated that irreversible pressure drop by the expansion is smaller for the PAM than water.3. As for two-phase flow pattern, bubble flow, slug flow and annular flow were observed in the wide channel. Bubble size for the bubble flow was smaller for the air-PAM flow than the air-water flow. The liquid film thickness between the gas phase and the channel walls for slug and annular flows was thicker for the air-PAM flow than the air-water flow, due to higher viscosity of the PAM.4. Pressure change across the sudden expansion in two-phase flow increased with increase in jG due to the significant effect of the expansion on the reversible pressure rise. The pressure change was larger for the PAM than water when jG is low. This indicated that the effect of the expansion on the flow disturbance is smaller at low jG for the PAM flows.5. Correlation by Shmidt and Friedel, which can account for liquid viscocity, gave the best predicton against the present data on the two-phase pressure change.
References
| [1] | Abdelall, F. F. et al. (2005). Pressure drop caused by abrupt flow area changes in small channels. Experimental Thermal and Fluid Science, 29, 425-434. |
| [2] | Böhm, L. et al. (2014). Rising behaviour of single bubbles in narrow rectangular channels in Newtonian and non-Newtonian liquids. International Journal of Multiphase Flow, 65,11–23. |
| [3] | Chen, I. Y. et al. (2007). Two-phase flow characteristics across sudden expansion in small rectangular channels. Experimental Thermal and Fluid Science, 32(8), 696-706. |
| [4] | Chen I. Y., et al. (2008). Two-phase flow characteristics across sudden expansion in small rectangular channels. Experimental Thermal and Fluid Science, 32(8), 1609-1619. |
| [5] | Chen, I. Y. et al. (2009). Two-phase flow pressure change subject to sudden expansion in small rectangular channels. International Journal of Multiphase Flow, 35(3), 297-306. |
| [6] | Collier, J.J. and Thome, J.R. (1994). Convective Boiling and Condensation, 3rd ed., Oxford, New York, 109-111. |
| [7] | Farooqi, S.I., et al. (1980). Rheological behavior of kaolin suspensions in water and water glycerol mixtures. Transactions of the Institution of Chemical Engineering, 58, 116-124. |
| [8] | Kozicki, W., Chou C.H., Tiu, C. (1996). Non-Newtonian flow in ducts of arbitrary cross-sectional shape. Chemical Engineering Science, 21, 665-679. |
| [9] | Sadatomi, M., Sato, Y. and Saruwatari, S. (1982). Two-phase flow in vertical noncircular channels. International Journal of Multiphase flow, 8(6), 641-655. |
| [10] | Sadatomi, M. et al. (2013). Air-water two-phase flow through U-bend, sudden expansion and sudden expansion in rectangular mini-channels. WIT Transactions on Engineering Sciences, 78, 63-75. |
| [11] | Shah, R.K., London, A.L. (1978). Laminar Flow Forced Convection in Ducts. Academic Press, New York. |
| [12] | Wadle, M., A. (1989). New formula for the pressure recovery in an abrupt diffuser, International Journal of Multiphase Flow, 15, 241-256. |
| [13] | Wang, C.C. et al. (2010). A new correlation and the review of two-phase flow pressure change across sudden expansion in small channels. International Journal of Heat and Mass Transfer, 53(19-20), 4287-4295. |




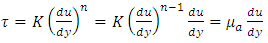
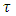 is the shear stress,
is the shear stress, 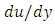 the shear rate, K the consistency coefficient, n the flow index and
the shear rate, K the consistency coefficient, n the flow index and 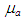
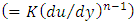 the apparent viscosity. In this study, the values of K and n for each test liquids were determined with a capillary method (Farooqi et al., 1980), and are listed in Table 2 together with the density and the surface tension. n for both water and PAM aqueous solution are investigated within the share rate range of 80 to 12000 1/s. In addition, the density and the surface tension are nearly the same between water and PAM aqueous solution. So, any changes in the test results are due mainly to the change in the viscosity of the test liquid.
the apparent viscosity. In this study, the values of K and n for each test liquids were determined with a capillary method (Farooqi et al., 1980), and are listed in Table 2 together with the density and the surface tension. n for both water and PAM aqueous solution are investigated within the share rate range of 80 to 12000 1/s. In addition, the density and the surface tension are nearly the same between water and PAM aqueous solution. So, any changes in the test results are due mainly to the change in the viscosity of the test liquid. 
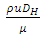 , where µ is the viscosity, u is the mean velocity). On the other hand, in the case of PAM aqueous solution, the generalized Reynolds number (Kozicki et al., 1966) was used to consider non-Newtonian properties, and this is given by:
, where µ is the viscosity, u is the mean velocity). On the other hand, in the case of PAM aqueous solution, the generalized Reynolds number (Kozicki et al., 1966) was used to consider non-Newtonian properties, and this is given by: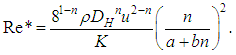
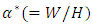 , for a rectangular channel:
, for a rectangular channel: 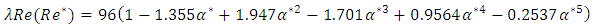


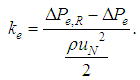
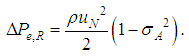
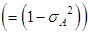 . As seen in this figure, the ke data gradually approach the calculation line with the increase in ReN or ReN*, and the water data in turbulent flow become almost constant and nearby the calculation line. The PAM data also approach the calculation line though no data was obtained in turbulent flow region.
. As seen in this figure, the ke data gradually approach the calculation line with the increase in ReN or ReN*, and the water data in turbulent flow become almost constant and nearby the calculation line. The PAM data also approach the calculation line though no data was obtained in turbulent flow region.


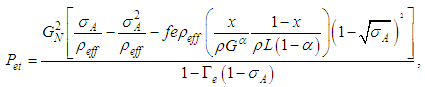
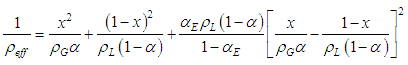
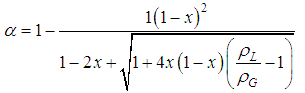
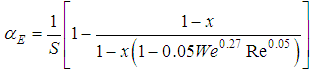
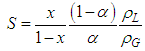
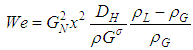
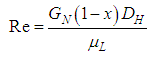
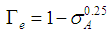
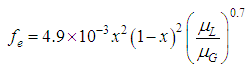
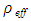 the effictive dencity in two-phase mixture,
the effictive dencity in two-phase mixture, 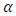 the void fraction. In addition,
the void fraction. In addition, 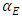 the mean volumetric entrainment, S are the slip ratio, We the Weber number, and
the mean volumetric entrainment, S are the slip ratio, We the Weber number, and 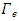 the base pressure coefficient, fe the friction factor in expansion.In the present calculation, non-Newtonian properties are taken into account by replacing
the base pressure coefficient, fe the friction factor in expansion.In the present calculation, non-Newtonian properties are taken into account by replacing 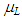 by apparent viscosity
by apparent viscosity 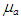 :
: 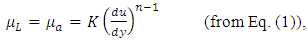
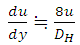

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

