1. Introduction

To optimize the shape of the insertion instruments used in laparoscopic surgery[1]-[3], the mechanical behavior of the insertion instruments and human body simulated material were examined during insertion. Body insertion instruments, attached with laparoscope and treatment tools, are tools which used to fix the abdominal wall, installation of required internal devices, etc. Moderate stiffness and good insertion into the body are therefore required. Furthermore, to optimize the shapes of the tip of the instruments being inserted into the human body, evaluation technology is required. The materials, structure and form have been reviewed in details[4], and also the method to reprocess has been studied[5]. In terms of surgical instrument required dynamic motion like a surgical clip, computational modeling and analysis for evaluating newly developed equipment has been recently reported[6].

However, regarding the human body materials, it has been obstacle in the development of virtual reality based surgical simulators that the data in current literature on material properties of soft tissues are not many enough[7][8]. Therefore, the efforts to obtain the properties of living human organs have being conducted by the measurement and simulation[9]. As the equipment for insertion, the other hand, there are many types of injection needle developed for reducing pain or for preventing the needle tip broken, however, the lack of design guideline and evaluating method for newly required insertion equipment through skin and muscle has become one of the issues.

In this study, insertion instruments having various tip shapes were inserted into the human body simulated materials, and the relationship between the load and displacement was determined to gain a quantitative understanding of the phenomenon.

2. Experimental

For the insertion instrument, a round bar having a diameter of 2.0 mm made of SUS303H was primarily used, and its tip shapes were roughly classified into two types: a cone type and a sharpened bamboo type. For comparison, a round bar with a diameter of 1.5 mm was also utilized. A sheet of silicon rubber of 10 mm-thickness, which is used in the field of medicine, was used as the material to simulate the human body[10][11]. This material was placed on top of a block made of Styrofoam with an opening having a diameter of 14 mm, as shown in Fig. 1. To measure the load and displacement of the human body insertion instrument, the Styrofoam blocks and the material representing the human body were placed on an electric balance, and the human body insertion instrument was then pushed into the material with a penetration rate of 1 mm per second.

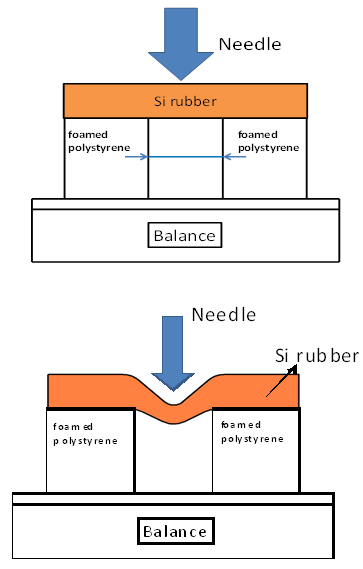Figure 1. Cross section of the experimental equipment

3. Result

3.1. Effect of Diameter and Tip Shape

Figure 2 shows an example of the relationship between the load and the displacement of the insertion instrument with a diameter of 2 mm. In this case, the tip of the instrument was processed in the shape of a sharpened bamboo tip for a tip length of up to 6 mm. As the displacement increased, the load gradually increased to a peak value just before penetration, after which it decreased to a constant value. The tip of the insertion instrument was pushed into the material, which was a soft silicone rubber. The material was then deflected like a circular plate which is subjected to a load concentrated at its center. When the applied stress exceeded the fracture stress of the material, the insertion instrument began to penetrate, and eventually, the motion nearly converges to a steady state when the instrument is tightened with an elastic force from the material.

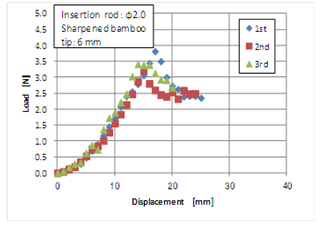Figure 2. Relationship between load and displacement of the insertion instrument with a diameter of 2mm in the shape of a sharpened bamboo tip for a tip length of up to 6 mm

Next, Fig. 3 shows the result when the insertion instrument used had the shape of a sharpened bamboo tip for a tip length of up to 18 mm. The load-displacement curves up to the peak exhibit similar behaviours to that of Fig. 2, but a steep reduction in the load is observed after the penetration. The suggested reason is that the cross-sectional area of the insertion instrument is smaller at a distance of more than 10 mm from the tip. When the elastic energy stored in the peak value is released with a small external force, the intrusion and penetration of the instrument progressed easily. In addition, the blades placed at the edges of the sides may also have contributed to the effect of shear stress caused by the friction force at the time of insertion[12].

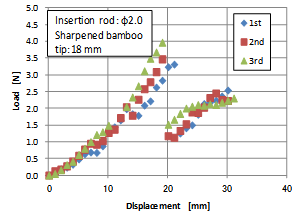Figure 3. Relationship between load and displacement of the insertion instrument with a diameter of 2mm in the shape of a sharpened bamboo tip for a tip length of up to 18 mm

Figure 4 shows the result when the tip was processed into a conical shape. Because the tip was not as sharp as that in Fig. 5, the peak of the load showed a high value of 4.5 N. The steady-state value after penetration was approximately 2.0 N, which is slightly lower than that in Figs. 2 and 3. This may be attributed to the larger size of the penetration hole, which may itself be affected by the shape of the tip.

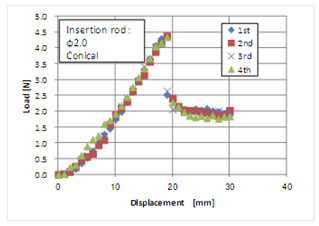Figure 4. Relationship between load and displacement of the insertion instrument with a diameter of 2mm in the shape of a conical

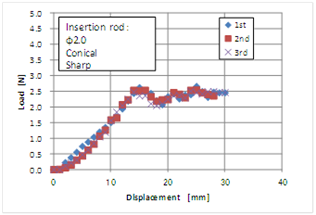Figure 5. Relationship between load and displacement of the insertion instrument with a diameter of 2mm in the shape of a sharp conical

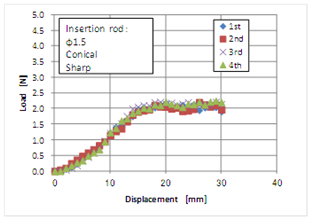Figure 6. Relationship between load and displacement of the insertion instrument with a diameter of 1.5 mm in the shape of a sharp conical

Figure 5 shows the empirical result of the load-displacement measurement for the insertion instrument whose tip has a conical shape similar to the original shape, but which is sharper than what was used in Fig. 4. The peak value of the load decreased to approximately 2.7 N, and therefore, it was confirmed that the shape of the tip significantly influenced the reduction of peak value.

Figure 6 shows the empirical result of the load-displacement measurement for the insertion instrument whose tip has a conical shape similar to the shape used in Fig. 5, and which has a diameter of 1.5 mm. Since the load at steady state decreased to approximately 2.0 N, it was also confirmed that reducing the diameter is effective for decreasing the load applied to the insertion instrument.

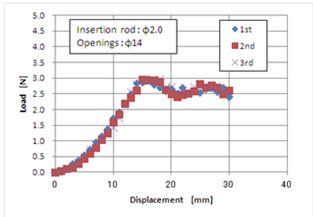
3.2. Influence of Opening Size and Addition of Liquid

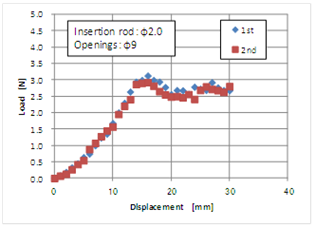
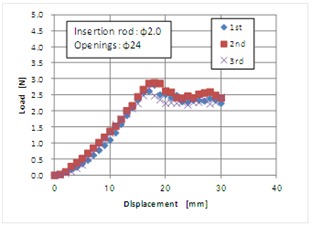
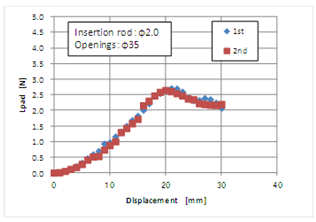
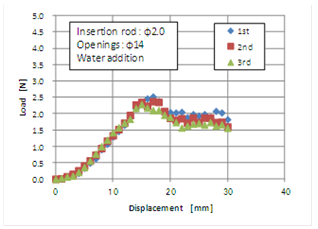
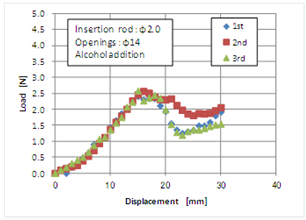
The insertion instrument used to obtain the experimental result is shown in Fig. 5, and it was used for another evaluation test, and subsequently reexamined. The result is shown in Fig. 7. The peak load increased slightly to approximately 0.3 N as a result of blunting of the tip because of frequent use. Using the insertion instrument as the reference for the following test, the influence of the opening size and the addition of liquid on the load-displacement curve were investigated. First, Figs. 8–10 show the results where the diameters of the openings were 9, 24, and 35 mm, respectively. In the case of an opening with diameter 9 mm, the load-displacement curve was not significantly different from that of the reference having an opening with a diameter of 14 mm, as shown in Fig. 5. When the opening diameter was increased to 24 and 35 mm, the gradient of the load-displacement curve for a small range of loads was reduced, and the displacement corresponding to the peak load was enhanced. This suggests that the deflection due to the material simulating the human body increased as the diameter of the openings increased. Furthermore, the peak load tends to decrease slightly with an increase in the diameter of the openings. This may be because the fracture of the material having a greater diameter begins under a load condition that is lower than that with smaller openings, thus a larger opening diameter results in a greater radial tensile force. Secondly, the influence of de-ionized water and isopropyl alcohol on the insertion behaviour was examined to consider practical conditions such as the presence of chemicals or body fluids. Figs. 11 and 12 show the effects of adding water and alcohol, respectively. When compared to the standard condition of Fig. 5, the addition of water causes a reduction in the peak load, and the steady-state load after penetration decreased, as shown in Fig. 11. The decrease in the latter may be because of the reduction of friction, and the reason for the gradual decrease in the load from the first to the second case may be because the wettability of the surface of the insertion instrument was gradually enhanced. In addition, the decrease in the peak load may have resulted in an increase in the spot stress around the tip owing to the reduction of the friction at the top of the insertion instrument. In Fig. 12, the result after adding alcohol is shown. The reduction of the peak load was also observed, as that with the addition of water. However, the load in the steady-state range decreased significantly the second and third time. It is believed that alcohol has a lower surface energy than water, i.e., the surface of the insertion instrument can easily show higher wettability, and furthermore, alcohol can penetrate the interface between the insertion instrument and the material that simulated the human body.

Figure 7. Relationship between load and displacement of the insertion instrument with a diameter of 2.0 mm in the shape of a sharp conical. The opening below the human body simulated material has a diameter of 14 mm

Figure 8. Relationship between load and displacement of the insertion instrument with a diameter of 2.0 mm in the shape of a sharp conical. The opening below the human body simulated material has a diameter of 9 mm

Figure 9. Relationship between load and displacement of the insertion instrument with a diameter of 2.0 mm in the shape of a sharp conical. The opening below the human body simulated material has a diameter of 24 mm

Figure 10. Relationship between load and displacement of the insertion instrument with a diameter of 2.0 mm in the shape of a sharp conical. The opening below the human body simulated material has a diameter of 35mm

Figure 11. Relationship between load and displacement of the insertion instrument with a diameter of 2.0 mm in the shape of a sharp conical, with the addition of isopropyl alcohol. The opening below the human body simulated material has a diameter of 14 mm

Figure 12. Relationship between load and displacement of the insertion instrument with a diameter of 2.0 mm in the shape of a sharp conical, with the addition of de-ionized water. The opening below the human body simulated material has a diameter of 14 mm

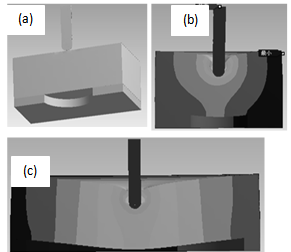Figure 13. Examples of three dimensional FEM analysis, (a) 3D-CAD model, (b) Opening: φ9mm, Load: 0.98N, (c) Opening: φ35mm, Load: 0.98N

4. Discussion

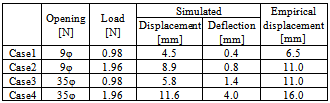
The material exhibited deformation behavior which was a combination of the insertion of the instrument and deflection of the material itself. To understand the whole deformation behaviour, a 3-dimensional elastic analysis was conducted since only the displacement of the insertion instrument and load were measured. ANSYS code was selected as a model that can handle elasticity and geometric nonlinearity. A hexagonal-dominant element was applied and the analytical scale had approximately 8000 elements and 18000 nodal points. The Young’s modulus of the human body simulated material was 0.102 MPa, and was obtained empirically by performing a tensile test. Calculated results are shown in Figs. 7–10, and a comparison between the empirical and the numerical simulation data was shown in Table 1. It was found that under the range of present conditions, the displacement of the insertion instrument is mainly because of the body of the insertion instrument in the material. The deflection of the material is not significant. Furthermore, because the simulation result is roughly consistent with the empirical data, we can understand

Table 1. A comparison between the empirical and the numerical simulation data of displacement of the insertion instrument and the deflection of the human body simulated material

5. Conclusions

Investigations of the relation between load and displacement were conducted when the instruments used in laparoscopic surgery were inserted into a human body simulated material. This was done by changing the diameter, tip shape of the instrument, and experimental conditions, and the phenomena was quantitatively discussed. Consequently, the basic guidelines for designing the shape of the insertion instrument were obtained as follows:

(1) First, the diameter of the instrument is determined by the required rigidity.

(2) To prevent the tip from being fractured or lost, it is required that the tip should be processed such that it has a minimum sharpness allowing it to penetrate into the material at an applied force, which is the steady-state load determined by the diameter of the insertion instrument.

(3) The addition of chemicals or body fluids significantly affected the above second condition.

Further study is required to quantify the sharpness of the tip and factors that affect the deformation model, because this study focused mainly on understanding the phenomena.

ACKNOWLEDGEMENTS

The authors thank Hariki Seiko Co., Ltd. in Okayama, Japan, for providing equipment and materials for testing.