-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2012; 2(6): 184-193
doi: 10.5923/j.jmea.20120206.09
Dynamic Effect of the Intermediate Block in a Hydraulic Control System
Yaozhong XU , Eric Bideaux , Sylvie Sesmat , Jean-Pierre Simon
Laboratoire Ampère, Institut National des Sciences Appliquées de LYON, Université de Lyon, Villeurbanne, 69621, France
Correspondence to: Yaozhong XU , Laboratoire Ampère, Institut National des Sciences Appliquées de LYON, Université de Lyon, Villeurbanne, 69621, France.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The intermediate block is a basic element in an hydraulic control system, and is usually used to install all hydraulic components and guides the fluid flows. However, the effect of this block is usually neglected, but it has to be taken into consideration when high performance applications, especially at high frequencies, have to be achieved. This paper focuses on this component and shows how it can influence the hydraulic system dynamics. The main contributions of this work are the implementation of a Bond Graph model of this component, which can easily be integrated in the whole system model, and a complete analysis of the effects (pressure drop, compressibility, inertia) induced by the intermediate block on the whole system performances. The relationship between flow rates and pressure drops along with the energy losses in the block are obtained according to a method based on the decomposition of the circuit in parts for which the local losses can be obtained from abacuses. The Computational Fluid Dynamics (CFD) is used for the validation of the results. Besides, the compressibility and inertial effects are carefully studied since they have a great influence on the hydraulic frequency. Finally, simulations and experiments are implemented for demonstrating the importance of the effect of the intermediate block in the hydraulic system modeling. By introducing compressibility and inertial effects of the intermediate block, the simulation result shows better agreement with experimental results at high frequencies. This comparison demonstrates that the control design can reach better performance when considering the dynamic model of the intermediate block.
Keywords: Intermediate Hydraulic Block, CFD, Bond Graph, Energy Dissipation, Compressibility Effect, Inertia Effect
Cite this paper: Yaozhong XU , Eric Bideaux , Sylvie Sesmat , Jean-Pierre Simon , "Dynamic Effect of the Intermediate Block in a Hydraulic Control System", Journal of Mechanical Engineering and Automation, Vol. 2 No. 6, 2012, pp. 184-193. doi: 10.5923/j.jmea.20120206.09.
Article Outline
1. Introduction
- In a typical hydraulic control system, the displacement of the actuator is piloted via a control element, such as a servovalve, which is connected to the actuator by an intermediate block. Moreover, most of the other hydraulic components required by the application are also installed on this block, for example accumulators, pressure sensors, electrovalves, flow reducers, etc.. This can lead to complex intermediate blocks, which may influence the whole system dynamics. Figure 1 shows the configuration of the inner circuit of the intermediate block in our test rig. The oil from the hydraulic pump is guided into the block after a filter, and then redirected towards the servovalve. Controlled by the servovalve, the flow is supplied to the actuator through the block. Besides, the block enables the system to alternate between three different working modes via the commutation of two electrovalves (V20 and V21):• Mode 1: a single 4-way servovalve to control the actuator; • Mode 2: two 4-way servovalves in parallel to control the actuator; • Mode 3: two 4-way servovalves with each servovalve used as a 3-way component to control the flow in one actuator chamber each. According to the working mode, the oil flows in different passages and crosses several inner tubes.
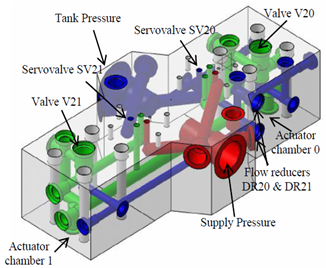 | Figure 1. Configuration of the inner tubes |
2. Modeling of the Intermediate Block
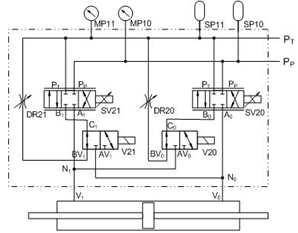 | Figure 2. Scheme of the hydraulic control system setup |
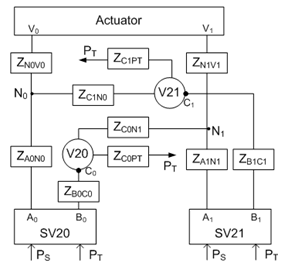 | Figure 3. Diagram of the different passages of the intermediate block |
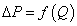 | (1) |
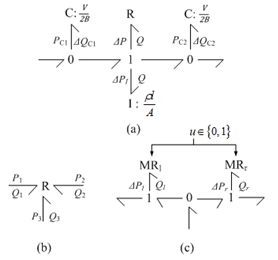 | Figure 4. Bond Graph model of (a) a passage, (b) a bifurcation and (c) a valve |
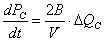 | (2) |
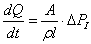 | (3) |
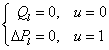 | (4) |
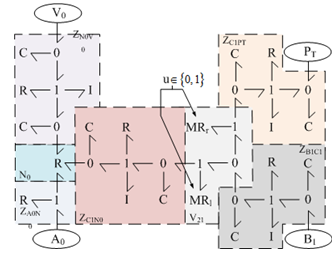 | Figure 5. Bond Graph model of the intermediate block for controlling a side of the actuator volume |
3. Energy Dissipation Calculation by Abacus-Based and CFD Methods
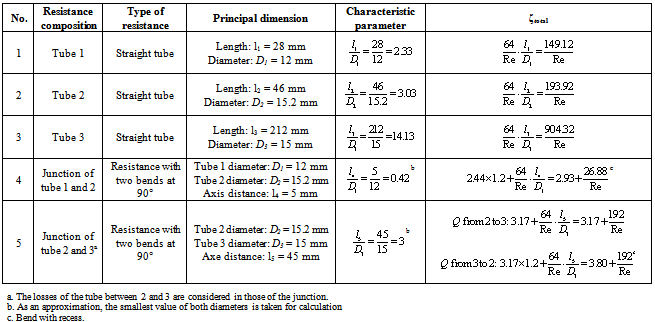
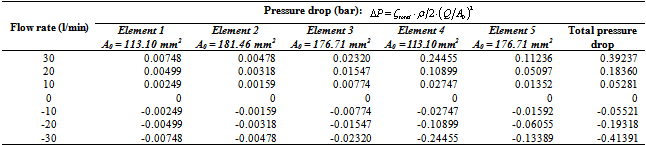
- The relationship between the flow rate and the pressure drop is complex in hydraulic systems. The energy dissipation depends not only on the local geometry and the fluid properties, but also on the Reynolds number which is a function of the flow velocity. It does not exist a unified formula valid for all cases. The CFD analysis enables to obtain the energy dissipation in the intermediate block but this method is difficult to apply for a lumped parameter approach. Indeed, boundary conditions to be set in the numerical model are not straightforward for the inner passages as these conditions change according to what happens in all the other passages. CFD is used here only to validate the results of the abacus-based method. This is done by comparing flow rates and pressure drops characteristics for each passage and their combinations. The CFD approach is used to determine the relationship of the flow rates and pressure drops with 3D geometric models. All passages mentioned in the previous section are exactly modeled and meshed. The boundary conditions are inlet and outlet pressure type for the single-input and single-output passages. Inlet velocity and outlet pressure boundary conditions are imposed to the bifurcations or to the passages containing a bifurcation so that the flow rate is determined at each port. Since the Reynolds number in the block is lower than 5000, laminar conditions are considered for the calculation.
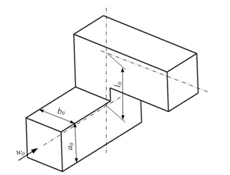 | Figure 6. Element formed by two bends assembled at an angle of 90° |
|
|
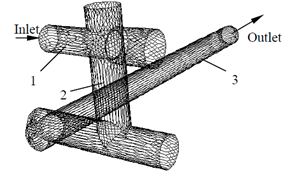 | Figure 7. Geometric model of the passage ZC0N1 |
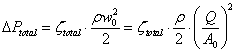 | (5) |
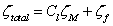 | (6) |
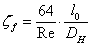 | (7) |
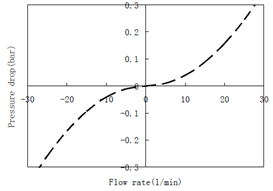 | Figure 8. ABM results of pressure drops versus flow rates in the passage ZC0N1 |
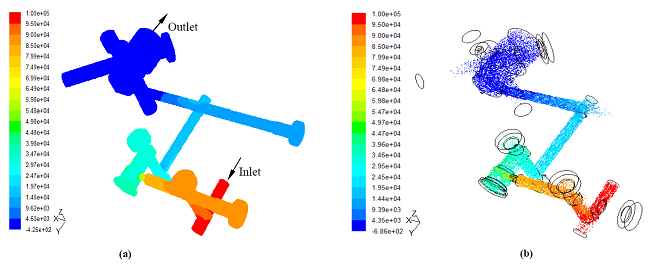 | Figure 9. Total pressures profile (a) and velocity evolution (b) of the passage ZC0PT in CFD analysis |
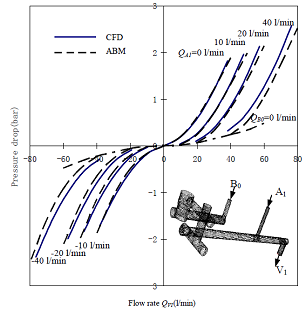
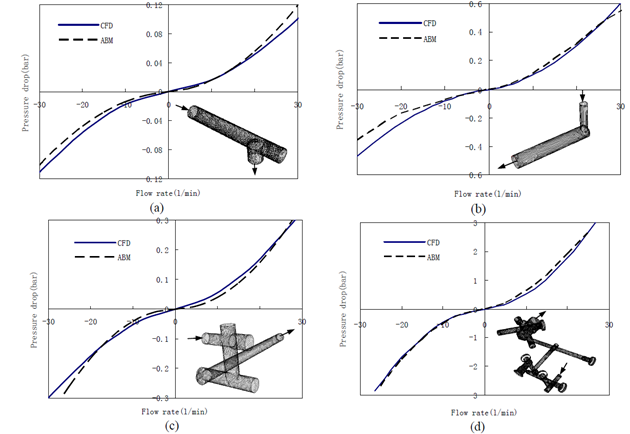 | Figure 10. CFD and ABM results of pressure drops with respect to flow rates: (a) ZN0V0; (b) ZB0C0; (c) ZC0N1; (d) ZC0PT |
4. Compressibility Effect of the Intermediate Block
- The volume of fluid in the intermediate block between the servovalve and the actuator induces a compressibility effect. This effect will influence the dynamics of the whole system and decrease the hydraulic pulsation. If the pressures in each passage are assumed to be identical, the volume effect of the intermediate block can be considered as an additional equivalent volume to each actuator chamber. The additional volume is the sum of the intermediate block volumes joint together. Therefore, although there is no flow in certain passages (ZC1N0 and ZB1C1) in mode 1, the additional volumes in modes 1 and 2 are the same as they have the same condition of the passage connection, i.e. the valves V20 and V21 in ON-position. Table 3 gives the calculated values of the additional volumes for each of the three working modes.
|
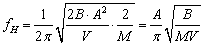 | (8) |
 | (9) |
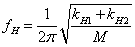 | (10) |
 | (11) |
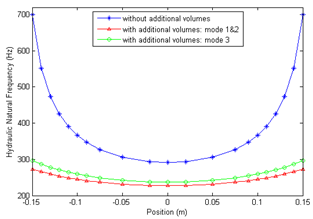 | Figure 12. Evolution of the hydraulic natural frequency of the actuator according to piston position with the effect of the intermediate block volumes |
5. Inertia Effect Study of the Intermediate Block
- Although the mass of fluid in the intermediate block is not important, the inertia effect can not be ignored, especially for a high performance system with a large bandwidth. This is mainly due to the small tube section in the intermediate block. The smaller the section is, the larger the velocity of the flow is, and then kinetic energy has to be taken into account. For ease of implementation of the block inertia effect into the dynamic model and to demonstrate its importance, an equivalent mass of fluid in the block is added to the mass of the moving part of the actuator. The kinematic energy of the hydraulic system is given by:
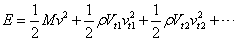 | (12) |
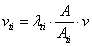 | (13) |
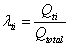 | (14) |
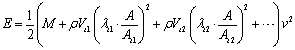 | (15) |
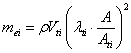 | (16) |
|
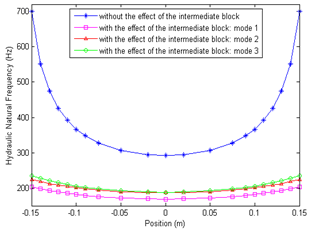 | Figure 13. Evolution of the hydraulic natural frequency of the actuator with the effect of the intermediate block |
6. Simulation and Experimental Results
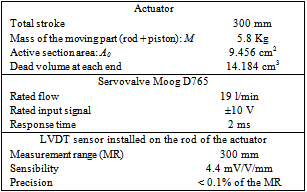
- Experiments have been conducted on a test bench equipped with a high performance actuator and two large bandwidth servovalves. These hydraulic components are implanted on the intermediate block. The test rig characteristics are presented in Table 6.
|
|
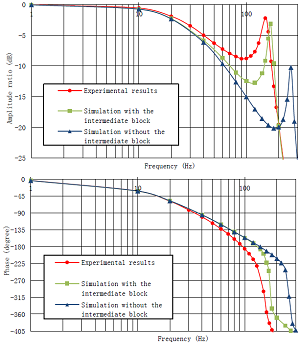 | Figure 14. Frequency responses of the system from simulations and experiments in mode 2 |
7. Conclusions
- This paper investigates the modeling of an intermediate block which would probably influence the performance of the hydraulic control system at high frequencies. The model including the compressibility effects, the fluid inertia, and the energy dissipation is developed using Bond Graph approach. Besides, an approach based on abacuses to determine the energy dissipation in each passage has been used and the results have been validated by comparison with CFD analysis. The characteristics of pressure drop versus flow rate were built, and gave the necessary parameters for the lumped parameter model of the intermediate block. Moreover, the compressibility and inertia effects of the intermediate block are studied and the calculated results illustrate that they can cause an obvious decrease in the hydraulic natural frequency. According to the simulation and experiment, we demonstrate that it makes sense to consider the effect of the intermediate block while modeling a hydraulic system with high performance and large bandwidth.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML