Hojat Khozeymehnezhad , Seyed Ali Mirbozorgi
University of Birjand, Department of Mechanical Engineering, Birjand, Iran
Correspondence to: Hojat Khozeymehnezhad , University of Birjand, Department of Mechanical Engineering, Birjand, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Numerical calculations are carried out for natural convection induced by a temperature difference between a cold outer square enclosure and a hot inner cylinder with two different geometries (i.e. circular and square). A two-dimensional solution for natural convection is obtained, using the finite volume method for different Rayleigh numbers varying over the range of (103–105). The study goes further to investigate the effect of vertical position of the inner cylinder on the heat transfer and flow field. The location of the inner cylinder is vertically changed along the center-line of the square enclosure. The number, size and form of the vortices strongly depend on the Rayleigh number and the position of the inner cylinder. The results show that for both cylinders, at low Rayleigh numbers of 103 and104, the bifurcation from the bicellular vortices to an uni-cellular vortex occurs when an inner cylinder is placed at a certain distance from the center of the enclosure. When Ra =105, only a uni-cellular vortex is formed in the enclosure irrespective of the position of the inner cylinder. Also as the obtained total surfaces-averaged Nusselt numbers of the enclosure show, in all cases, at the same Rayleigh number, the rate of heat transfer from the enclosure which the circular cylinder is located inside is better.
Keywords:
Natural Convection, Square Enclosure, Circular Cylinder, Square Cylinder, Different Vertical Locations, Finite Volume Method
Cite this paper: Hojat Khozeymehnezhad , Seyed Ali Mirbozorgi , Comparison of Natural Convection around a Circular Cylinder with a Square Cylinder Inside a Square Enclosure, Journal of Mechanical Engineering and Automation, Vol. 2 No. 6, 2012, pp. 176-183. doi: 10.5923/j.jmea.20120206.08.
1. Introduction
Natural convection in enclosures is encountered in many engineering systems such as convection in buildings, fluid movement in solar energy collectors, cooling of electronic circuits, and cooling of nuclear reactors, etc. Because of this wide range of applications, so far many studies have been performed in this field. For example: De and Dalal[1], studied numerically natural convection around a tilted heated square cylinder kept in an enclosure. Stream function– vorticity formulation of the Navier-Stokes equations was solved numerically using finite-difference method. Kim et al.[2], performed numerical simulation of natural convection induced by a temperature difference between a cold outer square enclosure and a hot inner circular cylinder. The immersed boundary method (IBM) was used to model an inner circular cylinder only at AR=0.2 in this paper. Lee et al.[3], carried out for natural convection induced by a temperature difference between a cold outer square cylinder and a hot inner circular cylinder numerically Rayleigh solution with immersed boundary method(IBM) for different numbers at different horizontal and diagonal locations for only one aspect ratio. The both effects of the inner cylinder location in an enclosure and the buoyancy-induced convection on heat transfer and fluid flow were investigated. Hussain and Hussein[4], investigated numerically the laminar steady natural convection where a uniform heat source applied on the inner circular cylinder enclosed in a square enclosure in which all boundaries are assumed to be isothermal. Hussain and Hussein[5], carried out a numerical simulation using a finite volume scheme for a laminar steady mixed convection problem in a two-dimensional square enclosure with a rotating circular cylinder enclosed inside it. The effects of various locations and solid-fluid thermal conductivity ratios on the heat transport process were studied in this work. Bararnia et al.[6], performed a numerical study of natural convection between a square outer cylinder and a heated elliptic inner cylinder. Lattice Boltzmann method (LBM) had been used to investigate the hydrodynamic and thermal behaviors of the fluid at various vertical positions of the inner cylinder for different Rayleigh numbers. Xu et al.[7], studied transient natural convective heat transfer of liquid gallium from a heated horizontal circular cylinder to its coaxial triangular enclosure numerically by employing the control volume method. Two orientations of the triangular cylinder were investigated in this paper.The above relevant literature survey shows that even though the fundamental features of natural convection inside enclosures have been identified and analyzed, in most cases, the effects of natural convection around inner cylinders of different geometries have not examined in detail. For example, there is no a comprehensive study that compre the natural convection around the circular cylinder with the square cylinder inside a square enclosure. Because of this, in the present study, different features of the natural convection around the two different geometries of cylinders inside an enclosure is numerically investigated for different Rayleigh numbers and different vertical locations of inner cylinders.
2. Physical Model and Assumptions
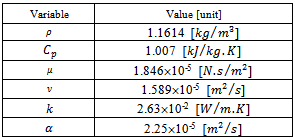
A schematic of the system considered in the present studyis shown in Fig. 1. The system consists of a square enclosure with sides of length H, where exists a circular cylinder with a radius R(=0.2H) or a square cylinder with diameter 2R. These inner cylinders can move along the vertical centerline of enclosure in the range of -0.2H to 0.2H. The walls of the square enclosure were kept at a constant low temperature of Tc, where as the cylinder was kept at a constant high temperature of Th. The fluid properties are also assumed to be constant, except for the density in the buoyancy term, which follows the Boussinesq approximation. In this paper, two different geometries of inner cylinders (i.e. circular and square) at three values of Rayleigh number (Ra =103,104 ,105) are considered. In the simulations to be reported here the Prandtl number, Pr, has been taken to be 0.7 corresponding to that of air. Since the present study would be a parametric study, the input data are adjusted so that the dimensionless parameters can take our desired values. Accordingly the cold temperature (Tc) was considered 300 K. All properties of the working fluid, namely air, which here is assumed to be an ideal gas, were chosen at temperature of 300 K and presented in Table 1.The enclosure length (H) was also considered as an input parameter and in this study, its value was determined 4 cm. It should be noted that the parameter Th is not given as an input parameter and it must be obtained from the following equation :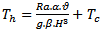 | (1) |
Table 1. Constants and thermo-physical properties
 |
| |
|
The dimensionless vertical distance δ, which represents the distance from center of the enclosure to the inner cylinder center along the vertical centerline,varies in the range of -0.2 –0.2.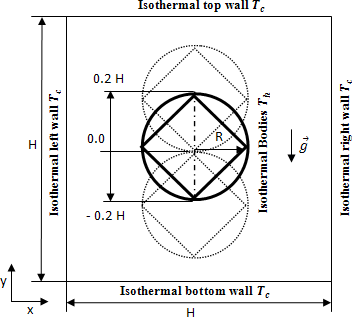 | Figure 1. Computational domain and coordinate system along with boundary conditions for both geometries |
3. Governing Equations
In order to state the governing equations in a dimensionless form, the following dimensionless variables are defined: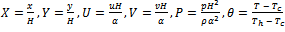 | (2) |
Based on the above dimensionless variables, the non-dimensional form of the equations for the conservation of mass, momentum and energy are :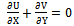 | (3) |
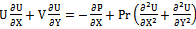 | (4) |
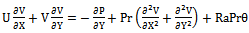 | (5) |
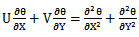 | (6) |
Where the Rayleigh, Ra and Prandtl, Pr numbers are defined as: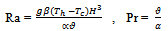 | (7) |
The dimensionless boundary conditions are :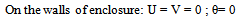 | (8) |
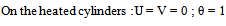 | (9) |
In the analysis, the average Nusselt number is defined as: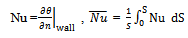 | (10) |
Where n is the normal direction with respect to the walls and S is distance along the square enclosure.
4. Numerical Method
The Figures 2 and 3 show algebraic generated grids around a circular cylinder and a square clinder inside a square enclosure respectively. These collocated, non-orthogonal grids based on finite volume technique have been applied for solution of the non-dimensional equations subjected to the boundary conditions. As it is observed in the Figures 2 and 3, the coarser grids are displayed for clarity. Near the walls of square enclosure and around the inner cylinder where a thin thermal boundary layer forms, a high grid concentration is required to resolve the temprature distribution accurately.  | Figure 2. A typical grid point distribution around a circular cylinder at δ=0. For clarity, a coarse grid is shown |
 | Figure 3. A typical grid distribution around a square cylinder at δ=0. For clarity, a coarse grid is shown |
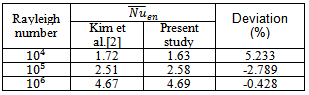
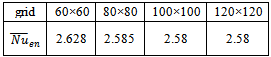
The diffusion terms in the equations are discretized by a second order central difference scheme, while a hybrid scheme is employed to approximate the advection terms. In order to link the velocity field and pressure in the momentum equations, the well known SIMPLEC-algorithm is adopted. The set of discretized equations are solved by TDMA line by line method[8].In order to valid the results of the developed numerical code, an atural convection problem with low temperature for enclosure and high temperature for inner circular cylinder was examined.The wall surface-averaged Nusselt number of enclosure for this test case were compared with the benchmark values by Kim et al.[2] as shown in Table 2. The comparison is carried out using the following dimensionless parameters: Pr=0.7, Ra =104–106 and δ=0. A good agreement is observed between the results.To perform the grid independence study, a case with circular cylinder at δ = 0 and Ra=105 is considered. Four different grids, namely, 60×60, 80×80, 100×100 and 120×120 are employed for the numerical calculations. The surface-averaged Nusselt number of square enclosure obtained by each kind of grids is shown in Table 3. As it can be seen, the 100×100 grid is sufficiently fine for the numerical calculation. The convergence criterion of solutions is satisfied when the normalized residual of all variables (u, v, p and T) goes to10-8.Table 2. Comparison between the surface-averaged Nusselt numbers of square enclosure obtained by the presente work with the results of Kim et al.[2]
 |
| |
|
Table 3. The surface-averaged Nusselt numbers of square enclosure for different grids
 |
| |
|
5. Results and Discussion
Figs. 4 and 5 show the streamlines and isotherms at Ra=104-105 and different vertical locations for circular and square cylinders respectively. Since the patterns of streamlines and isothrem lines at Ra=103 are almost similar to those at Ra=104, the resulted patterns at Ra=103 are not presented here for the sake of brevity. But if there is any difference between those, it will be mentioned.As shown in the figs. 4 and 5, in general, the heated lighter fluid goes upward between the hot surface of the inner cylinders and the vertical symmetry line until it encounters the cold top wall. Then the fluid becomes gradually colder and denser while it moves horizontally outward in contact with the cold top wall. Consequently, the cooled denser fluid descends along the cold side walls.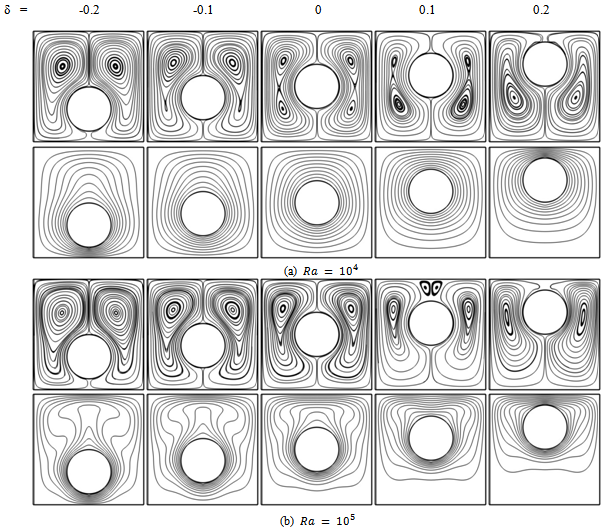 | Figure 4. Variations of isotherm lines and streamlines for circular cylinder at different δs and (a , (b) , (b) 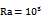 |
As shown in figs. 4(a) and 5(a) at δ=0 for Ra =104, the heat transfer in the enclosure is almost dominated by the conduction mode. The circulation of the flow shows two overall rotating symmetric eddies with two inner vortices inside each one of the left and right eddies. A careful observation in the figures shows that there is a small difference between inner vortices around the circular cylinder with those around the square cylinder. This difference is related to the size of these vortices, so that those around the square cylinder are larger than those around the circular cylinder. Because of more space in the enclosure around the square cylinder than the circular cylinder. As the Rayleigh number becomes 105 corresponding to figs. 4(b) and 5(b) for case of δ=0, the convection effect in heat transfer becomes more significant and the thermal boundary layer on the surface of the inner cylinder becomes thinner. Also, a plume starts to appear on the top of the inner cylinder. At this Rayleigh number, the flow filed undergoes a bifurcation where two inner vortices merge. The flow at the bottom of the enclosure is very weak compared with that at the middle and top regions which suggests stratification effects in the lower regions of the enclosure. At this Rayleigh number (i.e. Ra=105), similar to pervious cases, two vortices inside the enclosure around the square cylinder are larger than those the around the circular cylinder.As shown in figs. 4 and 5, When the cylinder moves downward, the size of the lower inner vortex is reduced gradually and the two inner vortices merge into a single vortex at δ = -0.1for circular cylinder and at δ = -0.2 for square cylinder at Ra=104. Because the space between the inner cylinders and the bottom wall of the enclosure diminishes in size. The reason of this difference in δs at Ra=104 is that the lower zone of enclosure around the square cylinder has more space thanit around the circular cylinder therefor the vortices have more space for circulation thus those disappear later. For Ra=103, two inner vortices merge into a single vortex at δ = - 0.2 for both cylinders.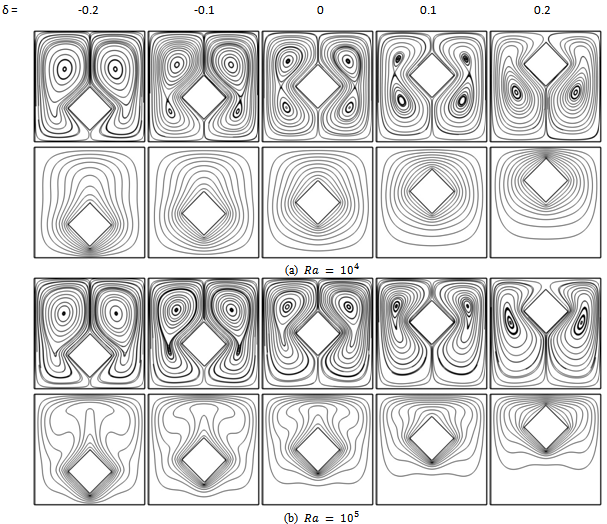 | Figure 5. Variations of isotherms lines and streamlines for square cylinder at different δs and (a) 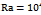 , (b) , (b) 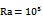 |
At Ra=105, when the cylinder moves downward more spaces between the hot inner cylinder and the top cold wall of the enclosure are secured, enhancing the buoyancy induced convection. Thus isotherms move upward and larger plumes exist on the top of the inner cylinder, which increase the thermal gradient on the top of the enclosure. The dominant flow is formed at the upper half of the enclosure, locating the core of the recirculating eddies in the upper half. The stagnant region under the inner cylinder decreases as δ becomes more negative, except for the two bottom corners of the enclosure. As shown in the figs. 4(a) and 5(a), When the cylinder moves upward, the bifurcation from the inner bi-cellular vortices to the uni-cellular vortex occurs at δ= 0.2 for both geometries but for the circular cylinder it is later than that for the case when the circular cylinder moves downward. This is because a stronger convective flow exists in the region between the hot inner cylinder and top wall of the enclosure. At Ra=105 corresponding to the fig. 4(b) and 5(b), When the inner cylinder moves upward, the pattern of isotherms and streamlines is much different from that when the innercylinder moves downward especially for circular cylinder. After the circular cylinder moves upward corresponding to fig. 4(b), isotherms at the upper half of the enclosure are slightly squeezed.When δ= 0.1, the plume at δ = 0 is divide into three plumes. Two upwelling plumes appear on the top of inner circular cylinder. A third plume appears above the top of the inner circular cylinder with reverse direction owing to the two secondary vortices newly generated over the upper part of the inner circular cylinder. As δ increases further, the reduced space above the top of the inner cylinder confines the vertical motion of flow and consequently the heat conduction is predominant over the convective heat transfer locally in this space. Thus, the secondary two vortices over the top of the inner cylinder decreases in size and finally disappears at δ = 0.2, and accordingly no third plume is found at this δ. For the square cylinder at Ra =105, when it moves upward, corresponding to fig. 5(b) at δ = 0.1, the plume at δ = 0 is divided into two upwelling plumes which appear on the top of square cylinder and no third plume appear in here.Figs. 6(a) and 6(b) show the distribution of local Nusselt numbers along the cold surfaces of the enclosure for both different geometries of cylinder and different δs at Ra=104 and Ra=105 respectively. Because the qualitative trend of diagrams for square cylinder is similar to circular cylinder and only the values of Nus for circular cylinder is larger than Those for square cylinder at the same δ. Thus in this figures, only the diagrams which is related to circular cylinder is explained. But there is any difference between them, it will be presented.In the fig. 6(a), when δ=0, the Nu has a maximum value at point A which is the stagnation point on the top wall of the enclosure. When we move from point A to B the Nu decreases and reaches a local minimum value close to zero at point B. When we move from point B to C the Nu increases, reaches a local maximum value at s=1where s is the distance from point A along the surfaces of the enclosure, and decreases again until it has a local minimum value at point C. When we move further from point C to D, the Nu increases slightly again. When the inner cylinder moves upward, the Nu at the upper half of the enclosure of 0 ≤ s ≤ 1 increases whereas that at the lower half of the enclosure of 1 ≤ s ≤ 2 decrease, compared to those when δ = 0. The variation of the Nu values in the region A-B according to the variation of δ is very large whereas that in the region B-C and region C-D is relatively small, due to the distribution of isotherms shown in Figs. 4(a) and 5(a).When the inner cylinder moves downward the distribution of the Nu shows almost symmetric shapes with respect to s=1 compared to when the inner cylinder moves upward. But in the region A-B, the location of the local Nusselt number maxima increases to the bottom wall direction.In the fig. 6(b), as it can be seen, the values of the Nus at Ra=105 is larger than those at Ra=103 and104, due to the increasing effect of convection. Correspondig to the fig. 6(b), when δ=0.1, there is a difference between two cylinders. For square cylinder, the trend of the distribution of the Nu is from a maximum to a minimum value because no secondary vortices appear on inner cylinder. But for circular cylinder, this trend is different due to secondary vortices appeared on the inner cylinder that it is explained in the following. For circular cylinder, the secondary eddies are formed on the upper surface of the inner cylinder. Thus the Nu at s = 0 (point A) when δ=0.1 is not the maximum in the presence of downwelling plume unlike to the cases of Ra = 103 and104. When we move from the point A to point B at δ=0.1, the Nu increases until it has a maximum value at the location with the upwelling plume and then decreases until it has a minimum value at s = 0.5 (point B). In the region A-B, the value of the Nu when δ=0.1 is smaller than that when δ=0. When δ increases to 0.2, the secondary eddies disappear. As are sult, when δ = 0.2, the Nu at s = 0 has a maximum value and decreases as we move from the point A to B until it has a minimum value at s = 0.5. In the region A–B, the value of the Nu when δ=0.2 is larger than that when δ=0 and increases with increasing δ. When we move from point B (s = 0.5) to point C (s = 1.5) at δ > 0, the Nu on the surface of the enclosure increases until it has the maximum and then keeps decreasing until it has a minimum value at s = 1.5. The Nu at δ > 0 does not change much and has an almost constant value close to zero, because the region C-D becomes stagnant when the inner cylinder moves upward. When the inner cylinder moves downward at Ra=105, the Nu is different from that when the inner cylinder moves upward. Because the secondary vortices do not exist on the upper surface of the inner cylinder, the Nu at δ < 0 has a maximum value at s = 0 (point A) and decreases as we move from point A to point B until it has a minimum value at s = 0.5 (point B). The Nu in the region of 0.5 ≤ s ≤ 1.5 at δ < 0 has a similar distribution to that at δ > 0. The difference in the value of the Nu in the region of 0.5 ≤ s ≤ 1.5 is not large for all the different values of δ. When we move from point C to point D, the Nu at δ < 0 increases with increasing s. The Nu on the bottom wall also increases very rapidly with increasing absolute value of δ at δ < 0 because the gap between the inner cylinder and the bottom wall keeps decreasing and the gradient of isotherms on the bottom wall increases very rapidly when the inner cylinder keeps moving downward.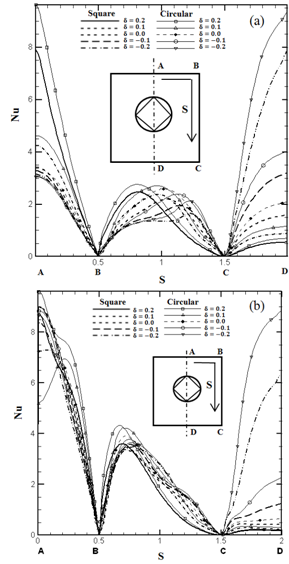 | Figure 6. Local Nusselt number distribution along (a) the surfaces of the enclosure for Ra = 104 and (b) the surfaces of the enclosure for Ra =105 at different positions of the inner cylinder for both cylinders (i.e. circular and square) |
Fig. 7 shows the total surfaces-averaged Nusselt number of the enclosure, 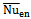 , as a function of δ at different Rayleigh numbers for both geometries of cylinder. When Ra = 103and104,
, as a function of δ at different Rayleigh numbers for both geometries of cylinder. When Ra = 103and104, 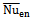 has a parabolic profile with a minimum value at δ = 0. The value of
has a parabolic profile with a minimum value at δ = 0. The value of 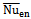 at Ra = 104 is almost the same as that at Ra =103. When the Rayleigh number increases to105, the symmetry of
at Ra = 104 is almost the same as that at Ra =103. When the Rayleigh number increases to105, the symmetry of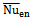 is broken and
is broken and 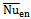 has a minimum value at δ = 0.1, because of the presence of the secondary vortices formed on the upper surface of the inner cylinder owing to the rising thermal plumes. In all cases studied, the value of
has a minimum value at δ = 0.1, because of the presence of the secondary vortices formed on the upper surface of the inner cylinder owing to the rising thermal plumes. In all cases studied, the value of 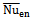 at δ= 0.2 is smaller than that at δ = -0.2, because the stagnant region at δ= 0.2 becomes larger than that δ = -0.2. As shown in the fig. 7, in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which the circular cylinder is located inside is better. The value of the Nu at Ra = 105 and δ= 0 is almost same for both cylinders. Because the patterns of streamline and isotherm are almost similar but when the cylinders move upward or downward, this similarity becomes less due to difference in patterns of streamline and isotherm especially streamline and also due to difference in space around the cylinders inside enclosure so that more space around the square cylinder cause the themal boundary layer thickness increases and then
at δ= 0.2 is smaller than that at δ = -0.2, because the stagnant region at δ= 0.2 becomes larger than that δ = -0.2. As shown in the fig. 7, in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which the circular cylinder is located inside is better. The value of the Nu at Ra = 105 and δ= 0 is almost same for both cylinders. Because the patterns of streamline and isotherm are almost similar but when the cylinders move upward or downward, this similarity becomes less due to difference in patterns of streamline and isotherm especially streamline and also due to difference in space around the cylinders inside enclosure so that more space around the square cylinder cause the themal boundary layer thickness increases and then 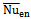 reduces. The optimal rate of heat transfer from the enclosure (i.e. maximum
reduces. The optimal rate of heat transfer from the enclosure (i.e. maximum 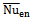 ) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0.
) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0.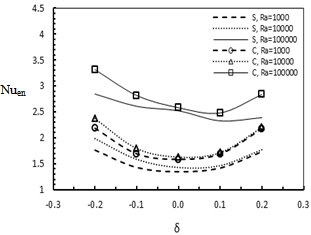 | Figure 7. Total surfaces-averaged Nusselt number of the enclosure, 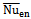 , along the δ for different Rayleigh numbers. (In the above figure, S namely square and C namely circular) , along the δ for different Rayleigh numbers. (In the above figure, S namely square and C namely circular) |
6. Conclusions
Free convection heat transfer around a heated cylinder with two different geometry in an air filled square enclosure investigated numerically. A parametric study was performed and the effects of the Rayleigh number and the position of the heated cylinder on the fluid flow and heat transfer were investigated. The results show that for both cylinders, at low Rayleigh numbers of 103 and 104, the bifurcation from the bicellular vortices to an uni-cellular vortex occurs when an inner cylinder is placed at a certain distance from the center of the enclosure. When Ra =105, only a uni-cellular vortex is formed in the enclosure irrespective of the position of the inner cylinder. At these high Rayleigh numbers, the effect of the inner cylinder position on fluid flow and heat transfer is significant, especially in the upper half region. For circular cylinder, when Ra=105, the secondary vortices due to the rising thermal plume from the inner cylinder are present on the upper surface of the inner cylinder.As the obtained  s show, The optimal rate of heat transfer from the enclosure (i.e. maximum
s show, The optimal rate of heat transfer from the enclosure (i.e. maximum 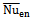 ) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0 and also in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which is located inside the circular cylinder is better.
) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0 and also in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which is located inside the circular cylinder is better.
Nomenclature
g = Gravitational acceleration, (m/s2)H = Length or width of the square enclosure, (m)n = Normal direction to the wall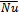 = Average Nusselt numberP = Dimensionless pressurePr = Prandtl numberR = Radius of circular cylinder, (m)Ra = Rayleigh numbers = Distance along the square enclosure, (m)T = Temperature, (°C)Tc = Temperature of the cold surface, (°C)Th = Temperature of the hot surface, (°C)k = Thermal conductivity (w/m.k)U = Dimensionless velocity component in x-directionu = Velocity component in x-direction, (m/s)V = Dimensionless velocity component in y-directionv = Velocity component in y-direction, (m/s)X = Dimensionless coordinate in horizontal directionx = Cartesian coordinate in horizontal direction, (m)Y = Dimensionless coordinate in vertical directiony = Cartesian coordinate in vertical direction, (m)
= Average Nusselt numberP = Dimensionless pressurePr = Prandtl numberR = Radius of circular cylinder, (m)Ra = Rayleigh numbers = Distance along the square enclosure, (m)T = Temperature, (°C)Tc = Temperature of the cold surface, (°C)Th = Temperature of the hot surface, (°C)k = Thermal conductivity (w/m.k)U = Dimensionless velocity component in x-directionu = Velocity component in x-direction, (m/s)V = Dimensionless velocity component in y-directionv = Velocity component in y-direction, (m/s)X = Dimensionless coordinate in horizontal directionx = Cartesian coordinate in horizontal direction, (m)Y = Dimensionless coordinate in vertical directiony = Cartesian coordinate in vertical direction, (m)
Greek Symbols
α = Thermal diffusivity, (m2/s)β = Volumetric coefficient of thermal expansion, (K-1)θ = Dimensionless temperatureν = Kinematic viscosity of the fluid, (m2/s)µ = dynamic viscosity of the fluid, (kg/m.s)ρ = Density of the fluid, (kg/m3)δ= distance from center of square cylinder to circular cylinder center, (m)
Subscripts
c = coldh = hoten = enclosure
References
| [1] | A.De, A.Dalal, "A numerical study of natural convection around a square, horizontal, heated cylinder placed in an enclosure." International Journal of Heat and Mass Transfer, vol.49, pp. 4608-4623, 2006. |
| [2] | B. Kim, D. Lee, M. Ha, H. Yoon,"A numerical study of natural convection in a square enclosure with a circular cylinder at different vertical locations." International Journal of Heat and Mass Transfer, vol.51, pp. 1888-1906, 2008. |
| [3] | J.M. Lee, M.Y. Ha, H.S. Yoon, "Natural convection in a square enclosure with a circular cylinder at different horizontal and diagonal locations." International Journal of Heat and Mass Transfer, vol.53, pp. 5905–5919, 2010. |
| [4] | S.Hussain, A.Hussein, " Numerical investigation of natural convection phenomena in a uniformly heated circular cylinder immersed in square enclosure filled with air at different vertical locations." International Communications in Heat and Mass Transfer, vol.37, pp. 1115–1126, 2010. |
| [5] | S. Hussain, A. Hussein,"Mixed convection heat transfer in a differentially heated square enclosure with a conductive rotating circular cylinder at different vertical locations. "International Communications in Heat and Mass Transfer, vol.38, pp. 263–274, 2011. |
| [6] | H.Bararnia, S.Soleimani, D.D.Ganji, "Lattice Boltzmann simulation of natural convection around a horizontal elliptic cylinder inside a square enclosure." International Communications in Heat and Mass Transfer, vol.38, pp. 1436–1442, 2011. |
| [7] | X.Xu, Z.Yu, Y.Hub, L.Fan, K. Cen, "Transient natural convective heat transfer of a low-Prandtl-number fluid from a heated horizontal circular cylinder to its coaxial triangular enclosure." International Journal of Heat and Mass Transfer, vol.55, pp. 995–1003, 2012. |
| [8] | S.V.Patankar, "Numerical heat transfer and fluid flow." Hemisphere Pub. Co. Washington. DC, 1980. |

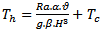

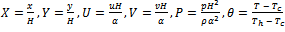
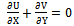
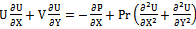
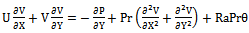
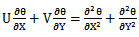
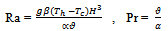
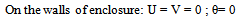
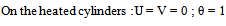
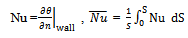



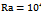 , (b)
, (b) 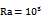

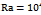 , (b)
, (b) 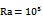
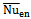 , as a function of δ at different Rayleigh numbers for both geometries of cylinder. When Ra = 103and104,
, as a function of δ at different Rayleigh numbers for both geometries of cylinder. When Ra = 103and104, 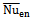 has a parabolic profile with a minimum value at δ = 0. The value of
has a parabolic profile with a minimum value at δ = 0. The value of 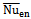 at Ra = 104 is almost the same as that at Ra =103. When the Rayleigh number increases to105, the symmetry of
at Ra = 104 is almost the same as that at Ra =103. When the Rayleigh number increases to105, the symmetry of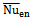 is broken and
is broken and 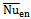 has a minimum value at δ = 0.1, because of the presence of the secondary vortices formed on the upper surface of the inner cylinder owing to the rising thermal plumes. In all cases studied, the value of
has a minimum value at δ = 0.1, because of the presence of the secondary vortices formed on the upper surface of the inner cylinder owing to the rising thermal plumes. In all cases studied, the value of 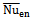 at δ= 0.2 is smaller than that at δ = -0.2, because the stagnant region at δ= 0.2 becomes larger than that δ = -0.2. As shown in the fig. 7, in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which the circular cylinder is located inside is better. The value of the Nu at Ra = 105 and δ= 0 is almost same for both cylinders. Because the patterns of streamline and isotherm are almost similar but when the cylinders move upward or downward, this similarity becomes less due to difference in patterns of streamline and isotherm especially streamline and also due to difference in space around the cylinders inside enclosure so that more space around the square cylinder cause the themal boundary layer thickness increases and then
at δ= 0.2 is smaller than that at δ = -0.2, because the stagnant region at δ= 0.2 becomes larger than that δ = -0.2. As shown in the fig. 7, in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which the circular cylinder is located inside is better. The value of the Nu at Ra = 105 and δ= 0 is almost same for both cylinders. Because the patterns of streamline and isotherm are almost similar but when the cylinders move upward or downward, this similarity becomes less due to difference in patterns of streamline and isotherm especially streamline and also due to difference in space around the cylinders inside enclosure so that more space around the square cylinder cause the themal boundary layer thickness increases and then 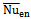 reduces. The optimal rate of heat transfer from the enclosure (i.e. maximum
reduces. The optimal rate of heat transfer from the enclosure (i.e. maximum 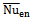 ) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0.
) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0.
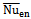 , along the δ for different Rayleigh numbers. (In the above figure, S namely square and C namely circular)
, along the δ for different Rayleigh numbers. (In the above figure, S namely square and C namely circular)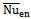 s show, The optimal rate of heat transfer from the enclosure (i.e. maximum
s show, The optimal rate of heat transfer from the enclosure (i.e. maximum 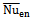 ) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0 and also in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which is located inside the circular cylinder is better.
) is at Ra=105 for circular cylinder at δ= -0.2. The worst case for rate of heat transfer is at Ra=103 for square cylinder at δ= 0 and also in all cases, at the same Rayleigh number, the rate of heat transfer from enclosure which is located inside the circular cylinder is better.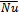 = Average Nusselt numberP = Dimensionless pressurePr = Prandtl numberR = Radius of circular cylinder, (m)Ra = Rayleigh numbers = Distance along the square enclosure, (m)T = Temperature, (°C)Tc = Temperature of the cold surface, (°C)Th = Temperature of the hot surface, (°C)k = Thermal conductivity (w/m.k)U = Dimensionless velocity component in x-directionu = Velocity component in x-direction, (m/s)V = Dimensionless velocity component in y-directionv = Velocity component in y-direction, (m/s)X = Dimensionless coordinate in horizontal directionx = Cartesian coordinate in horizontal direction, (m)Y = Dimensionless coordinate in vertical directiony = Cartesian coordinate in vertical direction, (m)
= Average Nusselt numberP = Dimensionless pressurePr = Prandtl numberR = Radius of circular cylinder, (m)Ra = Rayleigh numbers = Distance along the square enclosure, (m)T = Temperature, (°C)Tc = Temperature of the cold surface, (°C)Th = Temperature of the hot surface, (°C)k = Thermal conductivity (w/m.k)U = Dimensionless velocity component in x-directionu = Velocity component in x-direction, (m/s)V = Dimensionless velocity component in y-directionv = Velocity component in y-direction, (m/s)X = Dimensionless coordinate in horizontal directionx = Cartesian coordinate in horizontal direction, (m)Y = Dimensionless coordinate in vertical directiony = Cartesian coordinate in vertical direction, (m) Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


