Zohra Zidane 1, Mustapha Ait Lafkih 2, Mohamed Ramzi 2
1Laboratory of Automatic and Energy Conversion (LAEC) Electrical Engineering Department, Faculty of Sciences and Technology University of Sultan Moulay Slimane, B.P: 523 23000, Beni-Mellal, Morocco
2Electrical Engineering Department, Faculty of Sciences and Technology University of Sultan Moulay Slimane, B.P: 523 23000, Beni-Mellal, Morocco
Correspondence to: Zohra Zidane , Laboratory of Automatic and Energy Conversion (LAEC) Electrical Engineering Department, Faculty of Sciences and Technology University of Sultan Moulay Slimane, B.P: 523 23000, Beni-Mellal, Morocco.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Small hydro power is one of the most important renewable energy in the world. It does not encounter the problem of population displacement and is not as expensive as solar or wind energy. However, small hydro electrical generating units are usually isolated from the grid network; thus, they require control to maintain of constant the power for any working conditions. This paper presents a flow control approach for the speed control of hydro turbines. Power can be controlled by controlling the amount volume of water running into turbine. In this study, the adaptive predictive control is designed to control a flow for the automatic control of small hydro power plants. The standard Generalized Predictive Control (GPC) algorithm is presented. The Adaptive Generalized Predictive Control is then applied to achieve set point tracking of the output of the plant. A Single Input Single Output (SISO) model is used for control purposes. The model parameters are estimated on-line using an identification algorithm based on Recursive Least Squares (RLS) method. The performance of the proposed controller is illustrated by a simulation example of Small hydro power plant. Obtained results have shown better characteristics concerning both set point tracking and disturbance robustness for adaptive predictive control.
Keywords:
Adaptive Control, Generalized Predictive Control, Small Hydro Power Plant, Parameter Estimator
Cite this paper:
Zohra Zidane , Mustapha Ait Lafkih , Mohamed Ramzi , "Simulation Studies of Adaptive Predictive Control for Small Hydro Power Plant", Journal of Mechanical Engineering and Automation, Vol. 2 No. 6, 2012, pp. 169-175. doi: 10.5923/j.jmea.20120206.07.
1. Introduction
Small hydro power was one of the earliest small scale renewable energy technologies to be developed, and is still an important source of energy today. It has the potential to produce an important share of power, with a low price, more than solar or wind power. Small hydro electrical power plants are usually built in remote communities, as they use the river’s flow in the mountains. User loads require a uniform and an uninterrupted supply of input energy. In addition, small hydro powers are often isolated from grid networks. Thus, they require control to maintain of constant the power for any working conditions. Power can be controlled by controlling the amount volume of water running into turbine to produce just the necessary power [1-8]. It is well known that the mathematical model is very crucial for a control system design. For a small hydro power, there are many models to represent the machine behavior with a good accuracy. However, the parameters of the model are also important because the mathematical model cannot provide a correct behavior without correct parameters in the model. Therefore, the parameters can be determined by identification technique.This paper presents the application of Adaptive Generalized Predictive Control (GPC) to achieve set point tracking of the output of the plant. The Generalized Predictive Control (GPC) is one of the most favorite predictive control methods, popular in industry and also at universities. It was first published in 1987[9],[10]. The authors wanted to find one universal method to control different systems. GPC has been successfully implemented in many industrial applications, showing good performance and a certain degree of robustness. It is applicable[3] to the systems with non-minimal phase, unstable systems in open loop, systems with unknown or varying dead time, systems with unknown order and nonlinear systems approximated by linear models. The basic idea of GPC[12],[13] is to calculate a sequence of future control signals in such a way that it minimizes a multistage cost function defined over a prediction horizon. The index to be optimized is the expectation of a quadratic function measuring the distance between the predicted system output and some reference sequence over the horizon plus a quadratic function measuring the control effort. The predictive model is carried out based on the solving Diophantine equations.In the present paper the Adaptive Generalized Predictive Control method is designed to control a small hydro power plant and a Single Input Single Output (SISO) model is used for control purposes. The model parameters are estimatedOn-line using an identification algorithm based on Recursive Least Squares method. It is proved in the paper that in spite of important variations of the plant output; the developed adaptive structure maintains high level of performances (tracking, disturbance robustness and overshoot, cancellation of oscillation). The paper is organized as follows. Section II presents the Generalized Predictive Control algorithm. Section III is devoted the description of the adaptive control algorithm. In section IV, the effectiveness and superiority of the adaptive system, is demonstrated by simulation example. Some concluding remarks end the paper
2. Generalized Predictive Control Algorithm
The GPC scheme[14] can be seen in Figure 1. It consists of the plant to be controlled, a reference model that specifies the desired performance of the plant, a linear model of the plant, and the Cost Function Minimization (CFM) algorithm that determines the input needed to produce the plant’s desired performance. The GPC algorithm consists of the CFM block.The GPC system starts with the input signal, r(t), which is presented to the reference model. This model produces a tracking reference signal, w(t) that is used as an input to the CFM block. The CFM algorithm produces an output, which is used as an input to the plant. Between samples, the CFM algorithm uses this model to calculate the next control input, u(t+1), from predictions of the response from the plant’s model. Once the cost function is minimized, this input is passed to the plant. This algorithm is outlined below.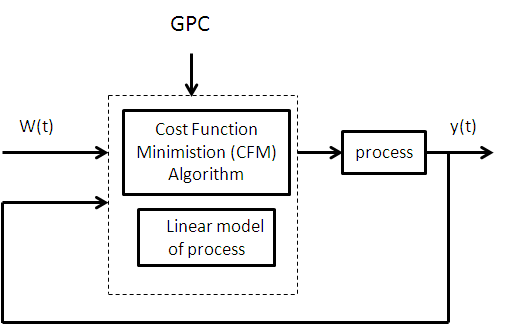 | Figure 1. Basic structure of GPC |
When considering regulation about a particular operating point, even a non-linear plant generally admits a locally-linearized model[9] and[10]: 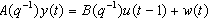 | (1) |
Where, A and B are polynomials in the backward shift operator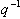 :
: 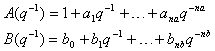 If the plant has a non-zeros dead-time the leading elements of the polynomial
If the plant has a non-zeros dead-time the leading elements of the polynomial 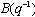 are zero. Where:u(t) is the control input.y(t) is the measured variable or output.w(t) is a disturbance term.In literature w(t) has been considered to be a moving average form:
are zero. Where:u(t) is the control input.y(t) is the measured variable or output.w(t) is a disturbance term.In literature w(t) has been considered to be a moving average form: 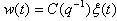 | (2) |
Where: 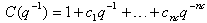 In this equation
In this equation 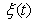 is uncorrelated random sequence, and combining with (1) we obtain the CARMA (Controlled Autoregressive Moving Average):
is uncorrelated random sequence, and combining with (1) we obtain the CARMA (Controlled Autoregressive Moving Average):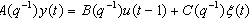 | (3) |
Where, is the differencing operator 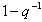 is the back shift operator such that
is the back shift operator such that 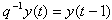 . For simplicity in the here
. For simplicity in the here 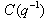 is chosen to be 1.The objective of the GPC control is the output y(t) to follow some reference signal y*(t) taking into account the control effort. This can be expressed in the following cost function: locally-linearized model[9] and[10]:
is chosen to be 1.The objective of the GPC control is the output y(t) to follow some reference signal y*(t) taking into account the control effort. This can be expressed in the following cost function: locally-linearized model[9] and[10]: 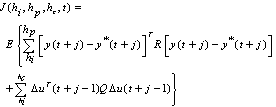 | (4) |
Where:hp is the prediction horizon.hi is the initial horizon.hc is the control horizon.y*(t) is the output reference. R is the output weighting factor.Q is the control weighting factor.The control objective is to compute at each time t, control inputs that minimize the quadratic criterion 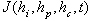 for this there are two cases:Let us first build j-step ahead predictors with following Diophantine equation:
for this there are two cases:Let us first build j-step ahead predictors with following Diophantine equation: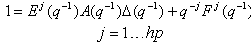 | (5) |
Where: 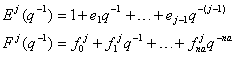 The polynomials
The polynomials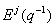 and
and 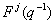 are uniquely defined by:
are uniquely defined by: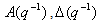 and j.Using equation (1) and (5) we obtain:
and j.Using equation (1) and (5) we obtain: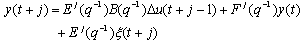 | (6) |
The optimal predictor, given measured output data up to time t and given u(t+i) for i>1, is clearly: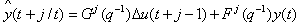 | (7) |
Where, 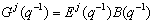 Defining
Defining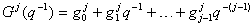 then the equation above can be written in the key vector form:
then the equation above can be written in the key vector form: 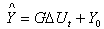 | (8) |
Where the vectors are all 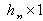 :
: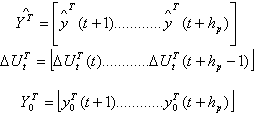 Note that
Note that 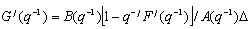 so that one way to computing
so that one way to computing 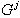 is simply to consider the Z-transform plant’s step-response and to take the first j terms and therefore
is simply to consider the Z-transform plant’s step-response and to take the first j terms and therefore 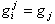 for j=0, 1, 2 …< i independent of the particular G polynomial[9].The matrix G is then lower-triangular of dimension
for j=0, 1, 2 …< i independent of the particular G polynomial[9].The matrix G is then lower-triangular of dimension 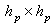 :
: Note that if the plant dead time d > 1 the first d-1 rows of the G will be null, but if instead hi is assumed to be equal to d the leading element is non-zero[1].From the definitions above of the vectors and with:
Note that if the plant dead time d > 1 the first d-1 rows of the G will be null, but if instead hi is assumed to be equal to d the leading element is non-zero[1].From the definitions above of the vectors and with: 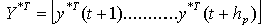 The expectation of the cost-function of (4) can be written as follow:
The expectation of the cost-function of (4) can be written as follow: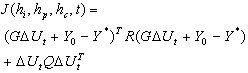 | (9) |
The solution, 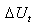 minimizing the criterion can be explicitly found, using:
minimizing the criterion can be explicitly found, using: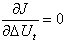 | (10) |
it follows that: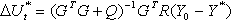 | (11) |
Note that the first element of 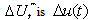 so that the current control u(t) is given by:
so that the current control u(t) is given by: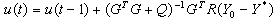 | (12) |
It is possible to reduce computational burden by imposing a constant control input vector after a fixed horizon hc 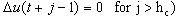 In this case the vector
In this case the vector 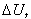 and the matrix G become:
and the matrix G become:
3. Adaptive Control Algorithm
The adaptive controller which is proposed here is indirect controller. To estimate the unknown system parameters  the Recursive Least Squares (RLS) algorithm parameter estimates
the Recursive Least Squares (RLS) algorithm parameter estimates  are using for tuning of the Generalized Predictive Controller. Thus, the obtained Adaptive Generalized Predictive Controller generates the current control signal.The following (RLS) algorithm has been using:
are using for tuning of the Generalized Predictive Controller. Thus, the obtained Adaptive Generalized Predictive Controller generates the current control signal.The following (RLS) algorithm has been using: | (13) |
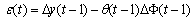 | (14) |
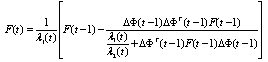 | (15) |
Where,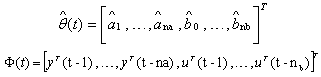 Where:
Where: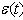 is the estimation error
is the estimation error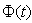 is the vector of data input-output F(t) is the adaptation gain
is the vector of data input-output F(t) is the adaptation gain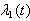 and
and 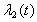 represents forgotten factors.
represents forgotten factors.
4. Simulation and Discussion
In order to illustrate the behavior of the above presented Adaptive Generalized Predictive Control, the simulation results of the small hydro power plant model obtained by using on-line identification technique, are given. The model is chosen as follows[15-17]: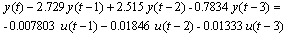 | (16) |
Several experiments have been carried out to determine a suitable control model order an appropriate sample time for control. A tried order model (na=3, nb=2, delay=0) sampled at 1 second gave a reasonable description of a small hydro power using on-line pilot plant dynamics.The simulation has been done with respect to the following considerations:• The sampling time T=1• The plant model structure na=3, nb=2 and delay=0• The reference is chosen as a square wave • The polynomial 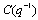 chosen as
chosen as 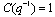 • The initial covariance matrix
• The initial covariance matrix 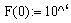 • The objective of the small hydro power control is to track a reference. The prediction controller parameters (hp, hc, hi, Q and R) are chosen in order to get an acceptable tracking.
• The objective of the small hydro power control is to track a reference. The prediction controller parameters (hp, hc, hi, Q and R) are chosen in order to get an acceptable tracking.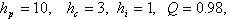 and R=1.First the non-disturbed small hydro power system is controlled by Adaptive Generalized Predictive Controller to track the set point. The tracking response is shown in figure 2 where we seen that the tracking performance is successfully achieved.Then, a step disturbance of 4 percent is injected in the small hydro power output. This quantity has been included in the output response as a forcing term to represent unmeasured disturbances. The system response is given in figure 4, where the tracking performance is achieved successfully and the effect of disturbance is well rejected.Then, the small hydro power output is affected by a random disturbance as shown in figure 6. It can be seen that the system response follows the reference with less oscillation.Finally, the plant was subjected to a step disturbance coupled with a Gaussian stochastic disturbance, as shown in figure 8, where the tracking performance is achieved successfully. It can be observed that the Adaptive Generalized Predictive Control shows better characteristics concerning the variances of the plant output and the control input. The behavior of the model’s parameters is shown in figures 3, 5, 7 and 9.
and R=1.First the non-disturbed small hydro power system is controlled by Adaptive Generalized Predictive Controller to track the set point. The tracking response is shown in figure 2 where we seen that the tracking performance is successfully achieved.Then, a step disturbance of 4 percent is injected in the small hydro power output. This quantity has been included in the output response as a forcing term to represent unmeasured disturbances. The system response is given in figure 4, where the tracking performance is achieved successfully and the effect of disturbance is well rejected.Then, the small hydro power output is affected by a random disturbance as shown in figure 6. It can be seen that the system response follows the reference with less oscillation.Finally, the plant was subjected to a step disturbance coupled with a Gaussian stochastic disturbance, as shown in figure 8, where the tracking performance is achieved successfully. It can be observed that the Adaptive Generalized Predictive Control shows better characteristics concerning the variances of the plant output and the control input. The behavior of the model’s parameters is shown in figures 3, 5, 7 and 9.
4.1. Case 1: Simulation in Noise Absence Conditions
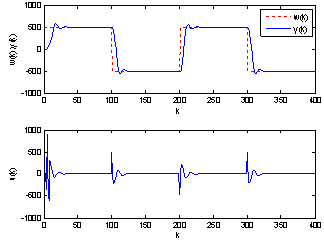 | Figure 2. Plant output and control input in noise absence conditions |
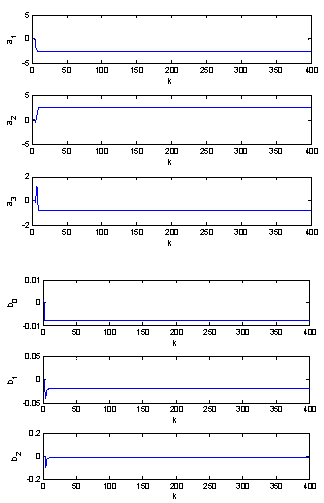 | Figure 3. Tuned parameters in noise absence conditions |
4.2. Case 2: Simulation in Noise Presence Conditions
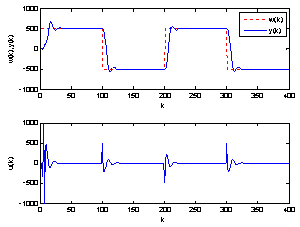 | Figure 4. Response of system affected by a step disturbance |
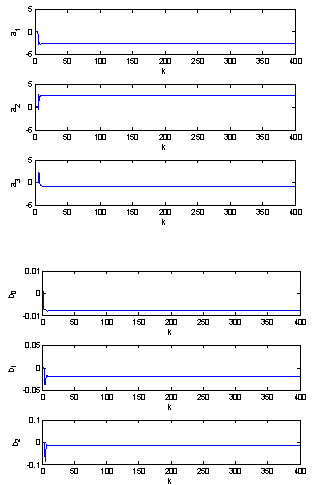 | Figure 5. Tuned parameters of the system affected by a step disturbance |
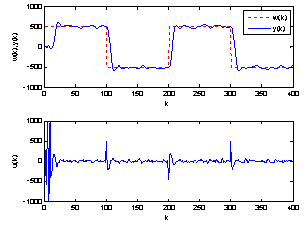 | Figure 6. Response of system affected by a random disturbance |
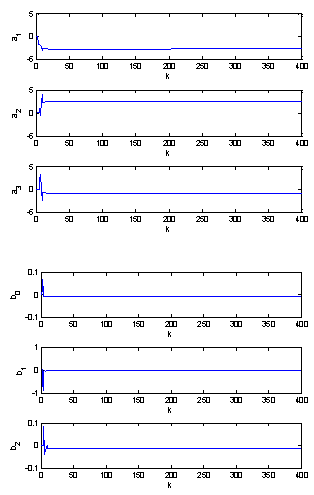 | Figure 7. Tuned parameters of the system affected by a random disturbance |
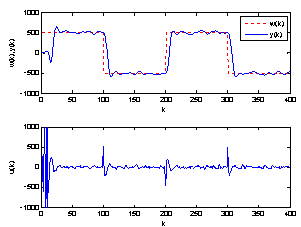 | Figure 8. Response of system affected by a step disturbance and a random disturbance |
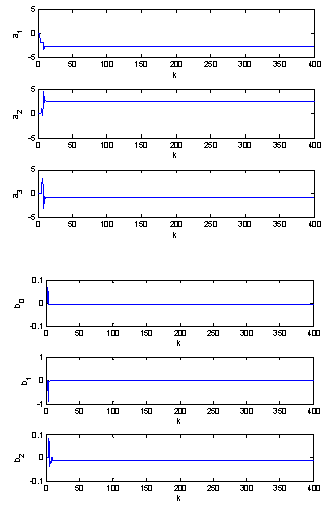 | Figure 9. Tuned parameters of the system affected by a step disturbance and a random disturbance |
5. Conclusions
Since Morocco has plenty of hydrological resources, it was aimed to contribute to the economical way to use water energy via improving Small Hydro Power pilot Plant. This paper, include better solution in term of efficiency and modern approach. The Adaptive Generalized Predictive Control strategy was proposed to maintain the power constant for any working conditions. The prediction model is designed using the Diophantine equations solution. It has proved that, even with important variations of the plant output, the developed adaptive structure maintains a high level of performances, in terms of tracking, disturbance robustness and overshoot, cancellation of oscillation. Thanks to using modern control, the productivity of the power system can be augmented; the machine and power plants are to be longer lived. Also, the pollution and CO2 emissions can be reduced. Finally, the efficiency of the proposed controller will be checked on an experimental test bench as soon as possible.
References
| [1] | Proceedings of the 6th Wseas Int. Conf. on Neural Networks, Lisbon, Portugal, pp. 1-4, June 16-18, 2005. |
| [2] | M. Hanmandlu, H. Goyal, “Proposing a new advanced control technique for micro hydro power plants”, Electrical power and Energy Systems. pp. 272-282, 30 2008 |
| [3] | M. Hanmandlu, H. Goyal, D.P. Kothari, “An Advanced Control Scheme for Micro Hydro Power Plants”, International Conference on Power Eletronis, Drives and Energy Systems, 2006. PEDES 06. pp.1-7, 12-15 Dec2006. |
| [4] | M. Chennani, S. Doubabi, “Study in simulation of the regulation and the improvement of the output of a micro hydroelectric power station”, ICM 05: Marrakesh, November 2005. |
| [5] | O. Daniel Quiroga, “Modelling and nonlinear control of voltage frequency of hydroelectric power plants”, doctoral thesis, Universidad Politécnica de Cataluna, Instituto de Organizacion y Control de Sistemas Industriales, July 2000. |
| [6] | DS. Henderson, “An advanced electronic load governor for control of Micro hydroelectric power generation”, IEEE Transactions Energy Conversion, Vol. 13, No. 3, September 1998. |
| [7] | C.D. Vournas, G. Papaionnou, “Modeling and stability of a hydro plant with two surge tanks,” IEEE Trans. Energy Conversion, vol. 10, no. 2, pp. 368-375, June 1995. |
| [8] | F. Hong-qing, S. Zu-yi, “Modeling and Simulation of Hydraulic Transients for Hydropower Plants,” 2005 IEEE/PES Transmission and Distribution Conference & Exhibition: Asia and Pacific Dalian, China |
| [9] | D. W. Clarke, C. Mohtadi, and P. S. Tuffs, "Generalized Predictive Control-part I. The Basic Algorithm", Automatica. Vol. 23, No. 2, pp. 137-148, 1987. |
| [10] | D. W. Clarke, C. Mohtadi, and P. S. Tuffs, "Generalized Predictive Control-part II. Extentions and Interpretations", Automatica. Vol. 23, No. 2, pp. 149-160, 1987. |
| [11] | P. Pivonka and P. Nepevny, "Generalized Predictive Control with Adaptive Model Based on Neural Networks", in Proceedings of the 6th Wseas Int. Conf. on Neural Networks, Lisbon, Portugal, pp. 1-4, June 16-18, 2005. |
| [12] | C. Bordons and E.F. Camacho, "A Generalized Predictive Controller for a wide class of industrial Processes", Vol 6, No. 2, pp 372-387, 1998. |
| [13] | N. Sepehri and G. Wu, "Experimental evaluation of Generalized Predictive Control Applied to a Hydraulic Actuator ", Robotica, Vol. 16, pp. 463-474, 1998. |
| [14] | S. Chidrawar and B. Patre, "Generalized Predictive Control and Neural Generalized Predictive Control", Leonardo Journal of Sciences, Issue 13, PP. 133-152, July-December, 2008. |
| [15] | H. Gao, C. Wang, “Effect of Detailed Hydro Turbine Models on Power System Analysis,” power systems conference and exposition, 2006. PCSE apos; 06. 2006 PES. pp: 1577-1581. |
| [16] | H. Goyal, T. S. Bhatti, and D. P. Kothari, A novel technique proposed for automatic control of small hydro power plants, International Journal of Global Energy Issues, 24 (1/2 ) , 2005 ,pp 29-46. |
| [17] | H. Goyal, T. S. Bhatti, and D. P. Kothari, An Artificial Intelligence based Approach for Control of Small Hydro power plants, Centre for Energy Studies, Indian Institute of Technology, Hauz Khas, New Delhi-110016 (India) |

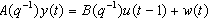
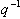 :
: 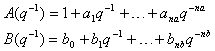 If the plant has a non-zeros dead-time the leading elements of the polynomial
If the plant has a non-zeros dead-time the leading elements of the polynomial 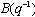 are zero. Where:u(t) is the control input.y(t) is the measured variable or output.w(t) is a disturbance term.In literature w(t) has been considered to be a moving average form:
are zero. Where:u(t) is the control input.y(t) is the measured variable or output.w(t) is a disturbance term.In literature w(t) has been considered to be a moving average form: 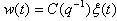
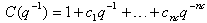 In this equation
In this equation 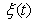 is uncorrelated random sequence, and combining with (1) we obtain the CARMA (Controlled Autoregressive Moving Average):
is uncorrelated random sequence, and combining with (1) we obtain the CARMA (Controlled Autoregressive Moving Average):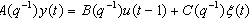
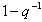 is the back shift operator such that
is the back shift operator such that 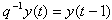 . For simplicity in the here
. For simplicity in the here 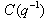 is chosen to be 1.The objective of the GPC control is the output y(t) to follow some reference signal y*(t) taking into account the control effort. This can be expressed in the following cost function: locally-linearized model[9] and[10]:
is chosen to be 1.The objective of the GPC control is the output y(t) to follow some reference signal y*(t) taking into account the control effort. This can be expressed in the following cost function: locally-linearized model[9] and[10]: 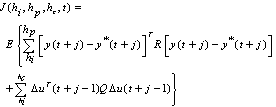
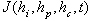 for this there are two cases:Let us first build j-step ahead predictors with following Diophantine equation:
for this there are two cases:Let us first build j-step ahead predictors with following Diophantine equation: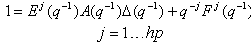
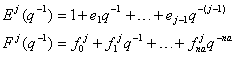 The polynomials
The polynomials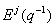 and
and 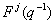 are uniquely defined by:
are uniquely defined by: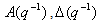 and j.Using equation (1) and (5) we obtain:
and j.Using equation (1) and (5) we obtain: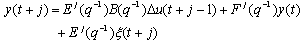
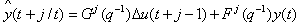
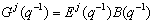 Defining
Defining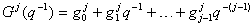 then the equation above can be written in the key vector form:
then the equation above can be written in the key vector form: 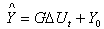
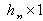 :
: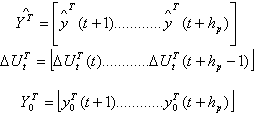 Note that
Note that 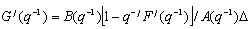 so that one way to computing
so that one way to computing 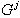 is simply to consider the Z-transform plant’s step-response and to take the first j terms and therefore
is simply to consider the Z-transform plant’s step-response and to take the first j terms and therefore 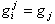 for j=0, 1, 2 …< i independent of the particular G polynomial[9].The matrix G is then lower-triangular of dimension
for j=0, 1, 2 …< i independent of the particular G polynomial[9].The matrix G is then lower-triangular of dimension 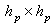 :
: Note that if the plant dead time d > 1 the first d-1 rows of the G will be null, but if instead hi is assumed to be equal to d the leading element is non-zero[1].From the definitions above of the vectors and with:
Note that if the plant dead time d > 1 the first d-1 rows of the G will be null, but if instead hi is assumed to be equal to d the leading element is non-zero[1].From the definitions above of the vectors and with: 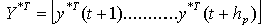 The expectation of the cost-function of (4) can be written as follow:
The expectation of the cost-function of (4) can be written as follow: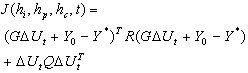
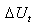 minimizing the criterion can be explicitly found, using:
minimizing the criterion can be explicitly found, using: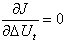
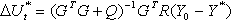
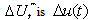 so that the current control u(t) is given by:
so that the current control u(t) is given by: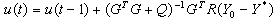
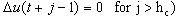 In this case the vector
In this case the vector 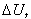 and the matrix G become:
and the matrix G become: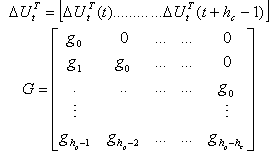
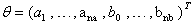 the Recursive Least Squares (RLS) algorithm parameter estimates
the Recursive Least Squares (RLS) algorithm parameter estimates 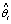 are using for tuning of the Generalized Predictive Controller. Thus, the obtained Adaptive Generalized Predictive Controller generates the current control signal.The following (RLS) algorithm has been using:
are using for tuning of the Generalized Predictive Controller. Thus, the obtained Adaptive Generalized Predictive Controller generates the current control signal.The following (RLS) algorithm has been using: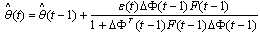
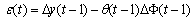
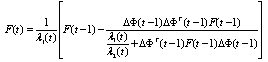
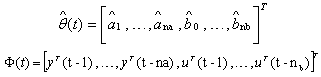 Where:
Where: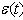 is the estimation error
is the estimation error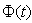 is the vector of data input-output F(t) is the adaptation gain
is the vector of data input-output F(t) is the adaptation gain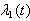 and
and 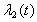 represents forgotten factors.
represents forgotten factors. 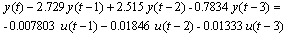
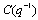 chosen as
chosen as 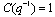 • The initial covariance matrix
• The initial covariance matrix 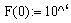 • The objective of the small hydro power control is to track a reference. The prediction controller parameters (hp, hc, hi, Q and R) are chosen in order to get an acceptable tracking.
• The objective of the small hydro power control is to track a reference. The prediction controller parameters (hp, hc, hi, Q and R) are chosen in order to get an acceptable tracking.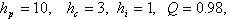 and R=1.First the non-disturbed small hydro power system is controlled by Adaptive Generalized Predictive Controller to track the set point. The tracking response is shown in figure 2 where we seen that the tracking performance is successfully achieved.Then, a step disturbance of 4 percent is injected in the small hydro power output. This quantity has been included in the output response as a forcing term to represent unmeasured disturbances. The system response is given in figure 4, where the tracking performance is achieved successfully and the effect of disturbance is well rejected.Then, the small hydro power output is affected by a random disturbance as shown in figure 6. It can be seen that the system response follows the reference with less oscillation.Finally, the plant was subjected to a step disturbance coupled with a Gaussian stochastic disturbance, as shown in figure 8, where the tracking performance is achieved successfully. It can be observed that the Adaptive Generalized Predictive Control shows better characteristics concerning the variances of the plant output and the control input. The behavior of the model’s parameters is shown in figures 3, 5, 7 and 9.
and R=1.First the non-disturbed small hydro power system is controlled by Adaptive Generalized Predictive Controller to track the set point. The tracking response is shown in figure 2 where we seen that the tracking performance is successfully achieved.Then, a step disturbance of 4 percent is injected in the small hydro power output. This quantity has been included in the output response as a forcing term to represent unmeasured disturbances. The system response is given in figure 4, where the tracking performance is achieved successfully and the effect of disturbance is well rejected.Then, the small hydro power output is affected by a random disturbance as shown in figure 6. It can be seen that the system response follows the reference with less oscillation.Finally, the plant was subjected to a step disturbance coupled with a Gaussian stochastic disturbance, as shown in figure 8, where the tracking performance is achieved successfully. It can be observed that the Adaptive Generalized Predictive Control shows better characteristics concerning the variances of the plant output and the control input. The behavior of the model’s parameters is shown in figures 3, 5, 7 and 9.







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML