Hani Aziz Ameen 1, Khairia Salman Hassan 2, Muwafaq Mahdi Salah 2
1Dies and Tools Eng. Dept. Technical College Baghdad , Iraq
2Mechanical Dept. Institute of Technology Baghdad , Iraq
Correspondence to: Hani Aziz Ameen , Dies and Tools Eng. Dept. Technical College Baghdad , Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This investigation explain the effects of annealing on the torsion aspects of carbon steel St.35. ANSYS12 software was used in investigation. Test specimens were prepared according to ASTM and heated with different temperature namely 850, 650, 450 and 150 °C for one hour and followed by cooling process via furnace. Microstructure and torsion test after heating were examined. It was found that increasing annealing temperature, the hardness decreased and torsion properties and consequently increasing the plastic depth and the optimum heat treatment conditions is annealing at 450°C which produce angle twist 680 deg compared with metal as received.
Keywords:
Torsion, Finite Element Analysis, ANSYS, Carbon Steel, Annealing
Cite this paper:
Hani Aziz Ameen , Khairia Salman Hassan , Muwafaq Mahdi Salah , "Experimental and Finite Element Investigation of Annealing on the Torsional Aspects of Carbon Steel St35", Journal of Mechanical Engineering and Automation, Vol. 2 No. 6, 2012, pp. 135-139. doi: 10.5923/j.jmea.20120206.03.
1. Introduction
Torsion tests are made on materials to determine such properties as the modulus of elasticity in shear and torsional yield strength, and may be carried out on full sized parts such as shafts, axles and twist drills. Little work on torsional data can be found. Heat treatment is the process of heating and cooling a metal in its solid state in order to obtain the desired properties.Hyoung, 2001,[1] performed a finite element analysis using a generalized axisymmetric element for the plastic deformation behaviour of cylindrical copper samples during torsion, the calculated hardness with the distance from the torsional axis is computed.Hafner et al, 2009[2] presented the article proposed an alternative way to compute the torsional stiffness based on three-dimensional continuum mechanics instead of applying a specific theory of torsion.Mahasneh et al, 2010[3] studied the effect of heat treatment on the torsion aspects of D2 alloy steel, in addition further analysis using finite element method was used in investigation. Sapountzakis and Tsipiras[4], developed a boundary element method for the nonuniform torsional vibration problem of bars of arbitrary doubly symmetric constant cross-section taking into account the effect of geometrical nonlinearity. The bar is subjected to arbitrarily distributed or concentrated conservative dynamic twisting and warping moments along its length. Beom-Seon Jang and Ming Ma[5], this study employs the Rayleigh–Ritz method to treat the elastic lateral-torsional buckling of the PMAstructure. Jang et al.[6], proposed a strength assessment procedure for PMA structure using a nonlinear finite element (FE) analysis and evaluated its structural adequacy by comparing the ultimate capacity with a set of actual stresses calculated by cargo hold analysis. This study proposes a formulation for elastic lateral- torsional buckling of PMA structure subjected to axial compression. Sapountzakis and V.J. Tsipiras[7] , the effect of axial restraint in the elastic_plastic uniform torsion analysis of cylindrical bars taking into account the effect of geometric nonlinearity is presented employing the boundary element method. Moreover, to the authors' knowledge the effect of axial restraint on the nonlinear elastic_plastic uniform torsion analysis has been examined only by Pi and Trahair[8] for the special case of homogeneous I-section thin walled beams employing the mitre model, while the boundary element method has only been employed by the authors of this paper[9], for the nonlinear elastic_plastic uniform torsion problem of homogeneous beams only for free axial boundary conditions. Sapountzakis and Tsipiras[10], developed a boundary element method for the evaluation of warping shear stresses of bars of an arbitrary doubly symmetric constant cross section undergoing nonuniform torsional vibrations taking into account the effect of geometrical nonlinearity. Sapountzakis et al.,[11- 14], in these works a boundary element method is developed for the nonuniform torsional vibration problem of bars of arbitrary doubly symmetric constant cross section, taking into account the effects of geometrical nonlinearity (finite displacement -small strain theory) and secondary twisting moment deformation.The overall objective in this study is to investigate the effect of different heat treatment on the torsional aspects of carbon steel St35.
2. Experimental Part
The experimental part is summarized as follows: A. Metal Selection A low carbon steel (St35) was chosen. By knowledge of the chemical composition of the metal, the metal is analyzed by an optical spectrograph. The chemical composition of the metal is shown in Table1. | Table 1. Chemical Composition of Carbon Steel (St35) |
| | Elem% , wt % | C | Mn | Si | Ni | Cr | Mo | S | P | | Actual value | 0.39 | 0.57 | 0.18 | - | 0.07 | - | - | - | | Stand. value | 0.32-0.39 | 0.5-0.6 | 0.4 | - | - | - | 0.045 | 0.095 |
|
|
B. Preparation of Test Specimen Many test specimen of steel used according to the standard specification for testing (ASTM standard D790-02) were prepared. The test specimen dimension is shown in Figure 1.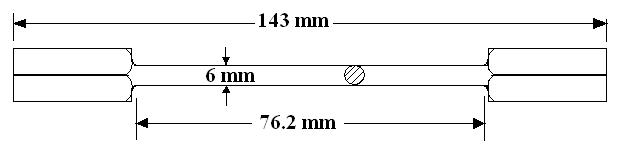 | Figure 1. Torsional Specimen |
C. Categorization of Specimen After complete preparation of the specimen (cutting the bar , manufacturing process), they are categorized into five groups as shown in table 2 .| Table 2. Categorization Of Specimen According To Groups |
| | State of Specimen | Specimen's symbol | | Specimen without heat treatment | A | | Specimen with heated 850 °C for one hour (full annealing ) | B | | Specimen heated 650 °C with one hour (spherical annealing ) | C | | Specimen heated 450 °C with one hour (recrystilization ) | D | | Specimen heated 150 °C with one hour (stress relief) | E |
|
|
D. Heat Treatment Annealing heat treatment was implemented on specimen groups (B,C,D,E) in Table2, which included heating the specimens to the specify temperature (850, 650, 450 and 150 ) ℃ for one hour and cooled slowly in the furnace. E. Microscopic Test Preparations of specimens for microscopic test inclusive: 1- Grinding the specimen by sand paper 180-240-400-800-1000 with use of water.2- Polishing operation by use a special polishing cloth with use of alumina solution (aluminum oxide Al2O3. The granules size is 0.3 µ). 3- Developing solutionfor the structure by use of Nital solution (2% nitric acid HNO3 with 98% methyl alcohol)4- Photographing the microstructure by a programmed microscope type (Metallurgical microscope MTj corporation) The photographs of microstructure of specimens A, B, C, D, and E are shown in Figure 2.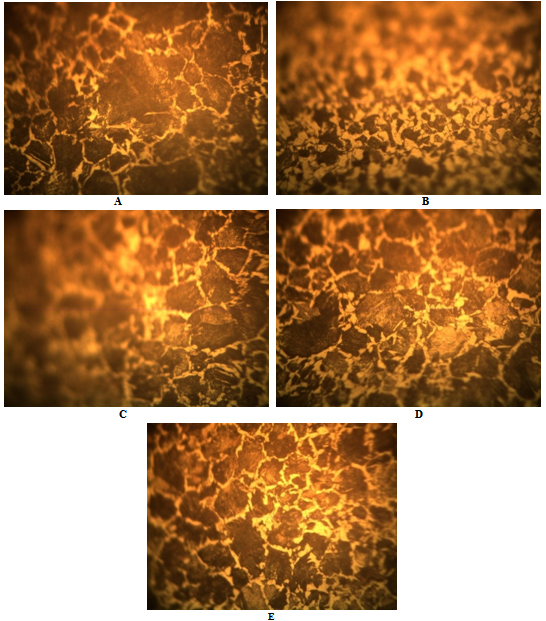 | Figure 2. The Photographs of Microstructure of Specimens A, B, C, D, And E |
3. Torsion Test
Torsion test is used to test the torsion of various types of materials. The specimens in Table2,fixed in the apparatus shown in Figure 3were subjected to torsion test.  | Figure 3. Torsion Device |
Firstly fixed the specimen in the device without any loading with balancing the water scale by putting the bubble air in the middle, at this time the disc and counter are nulls. Then the disc is turned and the angle is read with the corresponding force. Repeat this step with other angle and record the force. Figure 4 shown the experimental results for specimen’s group A, B, C, D, and E respectively.  | Figure 4. Torsional Specimen |
4. Finite Element Analysis
The objective is to determine the stress distribution at any cross- section.  and
and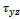 , it can be satisfied the following equation of equilibrium[15,16]: The total potential energy
, it can be satisfied the following equation of equilibrium[15,16]: The total potential energy  is defined as :
is defined as :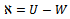 | (1) |
Where U is the strain energy and W is the work done ,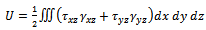 | (2) |
Substituting the shear stress and strain in term of Prandtls’ stress function  ,it can be deuced that:
,it can be deuced that: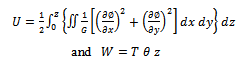 | (3) |
Where T is the applied torque and 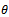 is the angle of twist per unit length, hence Eq.(1) will be
is the angle of twist per unit length, hence Eq.(1) will be 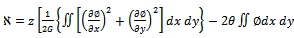 | (4) |
in order to get rid of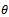 , let us define the warping function,
, let us define the warping function, 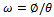 , and
, and 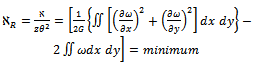 | (5) |
Assuming a solution in terms of nodal parameters, and for explicit form, it can be deduced that: 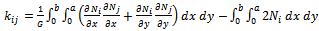 | (6) |
Where 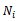 are the shape functions. The characteristic equation will be :
are the shape functions. The characteristic equation will be : | (7) |
ANSYS software was used to analyze the torsional specimen of steel St.35. Beam Element,BEAM188 is suitable for analyzing[17,18]. This element is based on Timoshenko beam theory (Eq.7). Shear deformation effects are included.BEAM188 is a linear (2-node) or a quadratic beam element in 3-D. BEAM188 has six or seven degrees of freedom at each node, with the number of degrees of freedom depending on the value of KEYOPT(1) (as shown in Figure 5). When KEYOPT(1) = 0 (the default), six degrees of freedom occur at each node. These include translations in the x, y, and z directions and rotations about the x, y, and z directions. When KEYOPT(1) = 1, a seventh degree of freedom (warping magnitude) is also considered. This element is well-suited for linear, large rotation, and/or large strain nonlinear applications. BEAM188 can be used with any beam cross-section defined via SECTYPE. The cross-section associated with the beam may be linearly tapered. A cross-section associated with this element type can be a built-up section referencing more than one material. Figure 6 shows the comparison between the experimental results and ANSYS results. Good agreement is evident with discrepancy 6% ,5%, 5%, 6.6% and 4.5?% for specimen A, B, C, D, and E. 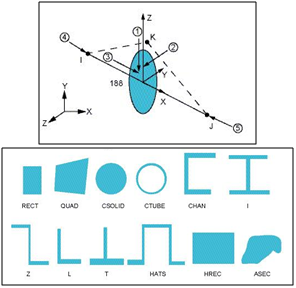 | Figure 5. Beam Element (Beam188 In Ansys) And Section Type[6] |
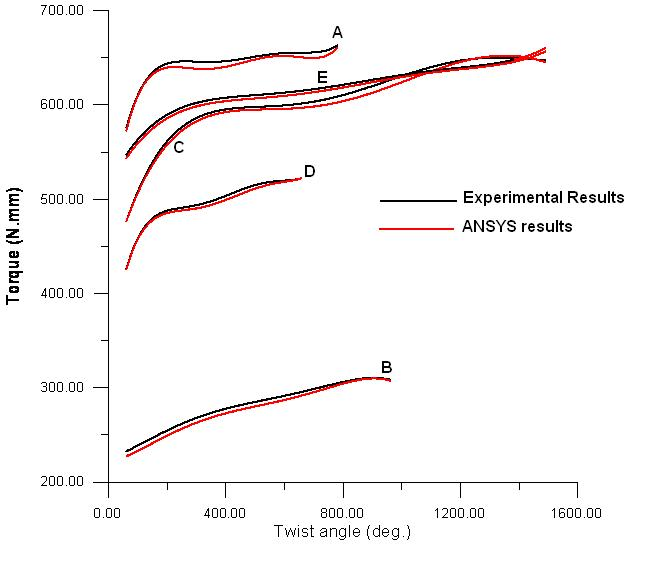 | Figure 6. Effect of Heat Treatment on Torsion Aspect of Carbon Steel St35 |
5. Discussion
The torsion results obtained from testing annealing heat treatment at different temperature. It can be deduced that annealing at 650°C indicated that the torsion strength during elastic limit was low comparing with the strength of the other. However the plastic depth was large during plastic zone because the total angle of twist was large this means that specimens deformed plastically in large amount when they were subjected to torsion load. From the result of annealing and torsion test the shear stress is considered as an important property which can be used in design and manufacture drill and tap because all these are subjected to torsion load in service. Usefulness of finding the value of shear stress to calculated the yield torque for any given diameter and from which the power of machine can be computed by following equation when rotational speed of machine known power equal the yield torque multiply by angular velocity. The other important factor is the plastic depth which can give the amount of plastic deformation which is very useful for heat treated metal, which is always showing less plastic deformation, thus the results present in Figure 6 indicate that the max. value of torsion for specimen group(C) .
6. Conclusions
1- Increasing annealing temperature hardness decrease and torsion properties and consequently increasing the plastic depth. 2- The best heat treatment temperature obtained from the test results at 450°C which produce angle twist 680 deg compared with metal as received.
References
| [1] | Hyoung S. K. “Finite Element Analysis of Torsional Deformation” , Materials Science and Engineering A299, 305–308, 2001. |
| [2] | Hafner S., Vogel F. and Konke C. “Finite Element Analysis of Torsion for ArbitraryCross-Sections” 18th International Conference on the Application of Computer Science and Mathematics in Architecture and Civil Engineering, Weimar, Germany, 07–09 July, 2009. |
| [3] | Mahasneh M.M. , Al-Qawabah S.M.A. and Al-Qawabeha U.F. “ Experimental and FEM Investigation of Heat Treatment on the Torsional Aspects of D2 Alloy Steel” , Research Journal of Applied Sciences, Eng. And Tech. , vol. 2, No. 6, PP 552-557, 2010. |
| [4] | E.J. Sapountzakis , V.J.Tsipiras “Nonlinear nonuniform torsional vibrations of bars by the boundary element method”, Journal of Sound and Vibration 329 (2010) 1853–1874 |
| [5] | Beom-Seon Jang , Ming Ma “Elastic lateral-torsional buckling analysis of permanent means of access structure”, Ocean Engineering 38 (2011) 1114–1122 |
| [6] | Jang, B.S., Chung, S.W., Ko, D.E., Chun, M.S., Kim, J.Y., 2009. A procedure for a strength assessment of permanent means of access structure. J. Soc. Nav. Archit. Korea 46 (1), 31–42. |
| [7] | E.J. Sapountzakis, V.J. Tsipiras “ Effect of axial restraint in composite bars under nonlinear inelastic uniform torsion by BEM”, Engineering Structures 31 (2009) 1190-1203. |
| [8] | Pi YL, Trahair NS. Inelastic torsion of steel I-beams. J Struct Eng ASCE 1995;121(4):609-20. |
| [9] | Sapountzakis EJ, Tsipiras VJ. Nonlinear inelastic uniform torsion of bars by BEM. Comput Mech 2008;42(1):77_94. |
| [10] | E.J. Sapountzakis , V.J. Tsipiras “Warping shear stresses in nonlinear nonuniform torsional vibrations of bars by BEM”, Engineering Structures 32 (2010) 741-752. |
| [11] | E.J. Sapountzakis · V.J. Tsipiras , “Shear deformable bars of doubly symmetrical cross section under nonlinear nonuniform torsional vibrations—application to torsional postbuckling configurations and primary resonance excitations” , Nonlinear Dyn (2010) 62: 967–987 |
| [12] | Sapountzakis, E., Dourakopoulos, J.: Flexural-torsional buckling analysis of composite beams by BEM including shear deformation effect. Mech. Res. Commun. 35, 497–516 (2008) |
| [13] | Sapountzakis, E., Dourakopoulos, J.: Shear deformation effect in flexural–torsional vibrations of beams by BEM. Acta Mech. 203, 197–221 (2009) |
| [14] | Sapountzakis, E., Dourakopoulos, J.: Nonlinear dynamic analysis of Timoshenko beams by BEM. Part I: Theory and numerical implementation. Nonlinear Dyn. 58, 295– 306 (2009) |
| [15] | Rao S. S. " The Finite Element Method in Engineering" Pergamon Press, 1982. |
| [16] | Smith I. M. and Griffths D.V. “Programming the Finite Element Method”, John Wiley, Inc, 1998. |
| [17] | User’s manual of FEA/ANSYS/ Version 12, 2010. |
| [18] | Nakasome Y., Yoshimoto S. and Stolarski T. “Engineering Analysis with ANSYS Software”,Elsevier Butterworth – Heinemann, 2006. |





 and
and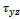 , it can be satisfied the following equation of equilibrium[15,16]: The total potential energy
, it can be satisfied the following equation of equilibrium[15,16]: The total potential energy  is defined as :
is defined as :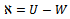
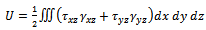
 ,it can be deuced that:
,it can be deuced that: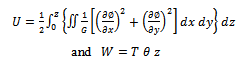
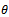 is the angle of twist per unit length, hence Eq.(1) will be
is the angle of twist per unit length, hence Eq.(1) will be 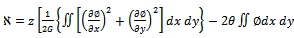
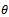 , let us define the warping function,
, let us define the warping function, 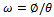 , and
, and 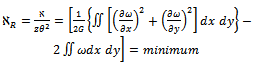
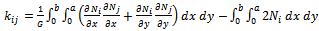
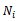 are the shape functions. The characteristic equation will be :
are the shape functions. The characteristic equation will be :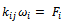


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML