-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2012; 2(6): 114-134
doi: 10.5923/j.jmea.20120206.02
Parametric Study of Nonlinear Beam Vibration Resting on Linear Elastic Foundation
Salih N Akour
Sustainable and Renewable Energy Program, College of Engineering, University of Sharjah, PO Box 27272, Sharjah, UAE
Correspondence to: Salih N Akour , Sustainable and Renewable Energy Program, College of Engineering, University of Sharjah, PO Box 27272, Sharjah, UAE.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Nonlinear beam resting on linear elastic foundation and subjected to harmonic excitation is investigated. The beam is simply supported at both ends. Both linear and nonlinear analyses are carried out. Hamilton’s principle is utilized in deriving the governing equations. Well known forced duffing oscillator equation is obtained. The equation is analyzed numerically using Runk-Kutta technique. Three main parameters are investigated: the damping coefficient, the natural frequency, and the coefficient of the nonlinearity. Stability regions for first mode analyses are unveiled. Comparison between the linear and the nonlinear model is presented. It is shown that first mode shape the natural frequency could be approximated as square root of the sum of squares of both natural frequency of the beam and the foundation. The stretching potential energy is proved to be responsible for generating the cubic nonlinearity in the system.
Keywords: Elastic Foundation, Nonlinear Beam, Parametric Study
Cite this paper: Salih N Akour , "Parametric Study of Nonlinear Beam Vibration Resting on Linear Elastic Foundation", Journal of Mechanical Engineering and Automation, Vol. 2 No. 6, 2012, pp. 114-134. doi: 10.5923/j.jmea.20120206.02.
Article Outline
1. Introduction
- Beams on elastic foundations received great attention of researches due to its wide applications in engineering. The model of the beam resting on a nonlinear support represents a large class of mechanical systems, such as, vibrating machines on elastic foundations, pipelines transversally supported, disc brake pad, shafts supported on ball, roller, or journal bearings, network of beams in the construction of floor systems for ships, buildings, bridges, submerged floating tunnels, railroad tracks etc. The elastic foundation for the beam part is supplied by the resilience of the adjoining portions of a continuous elastic structure.Hetenyi[1] and Timoshenko[2] presented an analytical solution for beams on elastic supports using classical differential equation approach, and considering several loading and boundary conditions.It is well known in engineering that a beam supported by discrete elastic supports spaced at equal intervals acts analogously to a beam on an elastic foundation and that the appropriateness of that analogy depends on the flexural rigidity of the beam as well as the stiffness and spacing of the supports. Ellington investigated conditions under which a beam on discrete elastic supports could be treated as equivalent to a beam on elastic foundation[3]. Beams resting on elastic foundations have been studied extensively over the years due to the wide application of this system in engineering. This system according to the literature can be divided at least into three categories. The first category is “linear beam on linear elasticfoundation”. Example of this type can be found inreferences[4]-[15]. The applications in this category include but not limited to Euler - Bernoulli beam, Timoshenko beam, Winkler foundation, Pasternak foundation, tensionless foundation, single parameter or two parameter foundation, static loading, harmonic loading and moving loading. For example the Winkler foundation model represents the simplest form of these types of beams. In this model the foundation is treated essentially as an array of closely spaced but non-interacting springs, each having a spring stiffness that equals the foundation modulus divided by the spacing between springs. The Pasternak foundation is extension of Winkler foundation by introducing shear interaction between springs. It is assumed that the top ends of the springs are connected to an incompressible layer that resists only transverse shear deformation. Tensionless foundation is similar to Winkler foundation but the springs do not carry any tension load.The second category is “linear beam on nonlinear elastic foundation[16]-[20]. In this category the foundation is considered to have nonlinear stiffness. Also this type includes different boundary and loading conditions according to the engineering application. The third category is nonlinear beam on linear elastic foundation[21]-[33]. Usually the beam nonlinearity means large deflections. Most of the studies related to this category have analyzed the system either using boundary element method or boundary integral equation method. Similar to the above two categories, there is wide variety of boundary and loading conditions being applied to such system according to the application.Nonlinear beam subjected to harmonic distributed load resting on linear elastic foundation is investigated in this research. The study is carried out in the view of the linearized model of the system. Well known duffing equation is obtained using Hamilton’s principle. Three main parameters are investigated: the damping coefficient, the natural frequency, and the coefficient of the nonlinear term. The effect of these parameters on the system stability is unveiled. Up to the author’s knowledge, this work is not published in the literature.
2. Problem Statement
- Nonlinear beam resting on elastic foundation that is shown in Fig. 1 is subjected to the following conditions:1. The beam material properties are linear.2. The damping (μ) and stiffness (kf) of the foundation are linear.3. The beam is slender and prismatic.4. The beam is simply supported (pin-pin ends)5. The load applied is harmonic and distributed over the length of the beam.
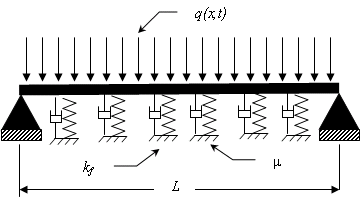 | Figure 1. schematic drawing of the beam on elastic foundation |
3. Mathematical Formulation
3.1. Kinetic Energy
- The rotary inertia of the beam will be neglected since the beam is slender.
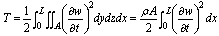 | (1) |
3.2. Potential Energy
- The potential energy due to bending can be calculated as the following:
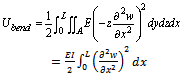 | (2) |
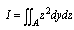 The formulation of the due to stretching potential energy can be casted as the following[35]:
The formulation of the due to stretching potential energy can be casted as the following[35]: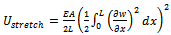 | (3) |
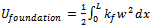 | (4) |
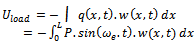 | (5) |
3.3. Derivation of Governing Equation
- The lagrangian is defined as the following:
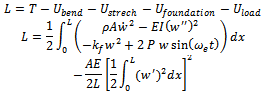 By applying Hamilton’s principle
By applying Hamilton’s principle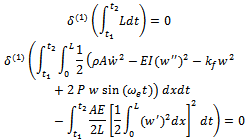 Denote the first and the second integral by F1 and F2 respectively. This gives
Denote the first and the second integral by F1 and F2 respectively. This gives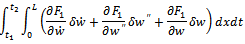
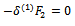 Integrating the first and the second term by parts with respect to x the result is the following equation:
Integrating the first and the second term by parts with respect to x the result is the following equation: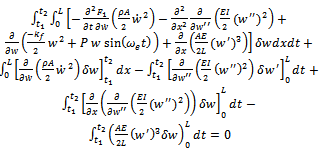 | (6) |
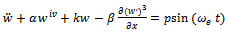 | (7) |
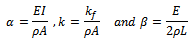 It is obvious that Equation (7) is the duffing oscillator equation. This equation is going to be recasted into a more familiar form in the next section. The boundary and initial conditions can be obtained from the remaining terms in Equation (6).The boundary conditions at x=0 and x=L are
It is obvious that Equation (7) is the duffing oscillator equation. This equation is going to be recasted into a more familiar form in the next section. The boundary and initial conditions can be obtained from the remaining terms in Equation (6).The boundary conditions at x=0 and x=L are | (8a) |
 | (8b) |
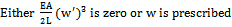 | (8c) |
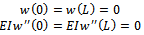 These boundary conditions must be satisfied by the mode shapes of the system. This fact will be used in the following sections as the criteria for selecting the form of the mode shape equation.Finally the initial conditions for
These boundary conditions must be satisfied by the mode shapes of the system. This fact will be used in the following sections as the criteria for selecting the form of the mode shape equation.Finally the initial conditions for 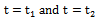 are
are  In this case, it will be assumed that the system starts from rest i.e. the initial displacement and velocity is zero.
In this case, it will be assumed that the system starts from rest i.e. the initial displacement and velocity is zero.3.4. Discretization and linearization
- The following expression is used for w(x, t) in order to discretize the problem
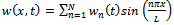 | (9) |
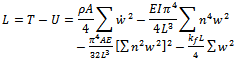 | (10) |
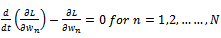 | (11) |
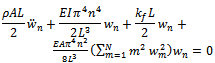 | (12) |
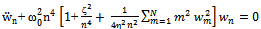 | (13) |
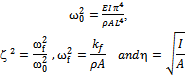 Writing Equation (13) for a single mode and inserting the linear damping term gives,
Writing Equation (13) for a single mode and inserting the linear damping term gives,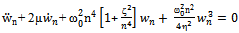 | (14) |
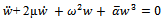 | (15) |
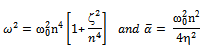 In order to linearize the system for the first mode (n=1) the system is converted into first order ordinary differential equations by the following substitution
In order to linearize the system for the first mode (n=1) the system is converted into first order ordinary differential equations by the following substitution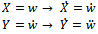 Applying this to Equation (15)
Applying this to Equation (15) 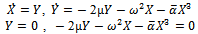 From the above equations it is obvious that (0, 0) is the only critical point for the system. So the equivalent linear system is obtained by expanding the above equation using Taylor series about (0, 0), so the remaining linear terms are
From the above equations it is obvious that (0, 0) is the only critical point for the system. So the equivalent linear system is obtained by expanding the above equation using Taylor series about (0, 0), so the remaining linear terms are 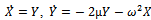 The corresponding Jacobi matrix is
The corresponding Jacobi matrix is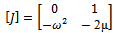 So the Eigenvalues of J are
So the Eigenvalues of J are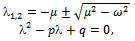 where
where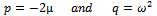 Introducing Δ as
Introducing Δ as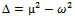 the following can be said about (0, 0):a. For
the following can be said about (0, 0):a. For 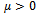 :Stable attractive node for
:Stable attractive node for 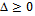 Stable spiral attractive node
Stable spiral attractive node 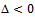 b. Stable center if
b. Stable center if 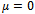 ;c. Unstable if
;c. Unstable if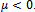 .The general solution of the linearized unforced system is
.The general solution of the linearized unforced system is 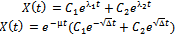 Applying the initial conditions
Applying the initial conditions 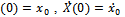 the constants of integration are going to be as the following:
the constants of integration are going to be as the following: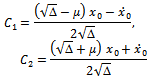
3.5. Simulation of the Nonlinear System
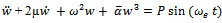 | (16) |
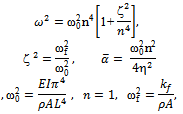 and
and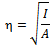 It is obvious that the strength of the nonlinearity is inversely proportional to the square of the radius of gyration of the beam. This indicates that the nonlinearity remains weak as long as the beam is relatively slender as assumed in this study. Finally, the frequency equation can be simplified to
It is obvious that the strength of the nonlinearity is inversely proportional to the square of the radius of gyration of the beam. This indicates that the nonlinearity remains weak as long as the beam is relatively slender as assumed in this study. Finally, the frequency equation can be simplified to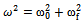 .The apparent natural frequency of the system ω is the square root of the sum of the squares of the natural frequencies of the beam and the elastic foundation. The nonlinear second order ordinary differential equation is converted into a system of first order ordinary differential equations. This is suitable for numerical study using Runge-Kutta Techniques.
.The apparent natural frequency of the system ω is the square root of the sum of the squares of the natural frequencies of the beam and the elastic foundation. The nonlinear second order ordinary differential equation is converted into a system of first order ordinary differential equations. This is suitable for numerical study using Runge-Kutta Techniques. 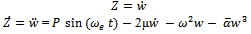 | (17) |
4. Results and Discussion
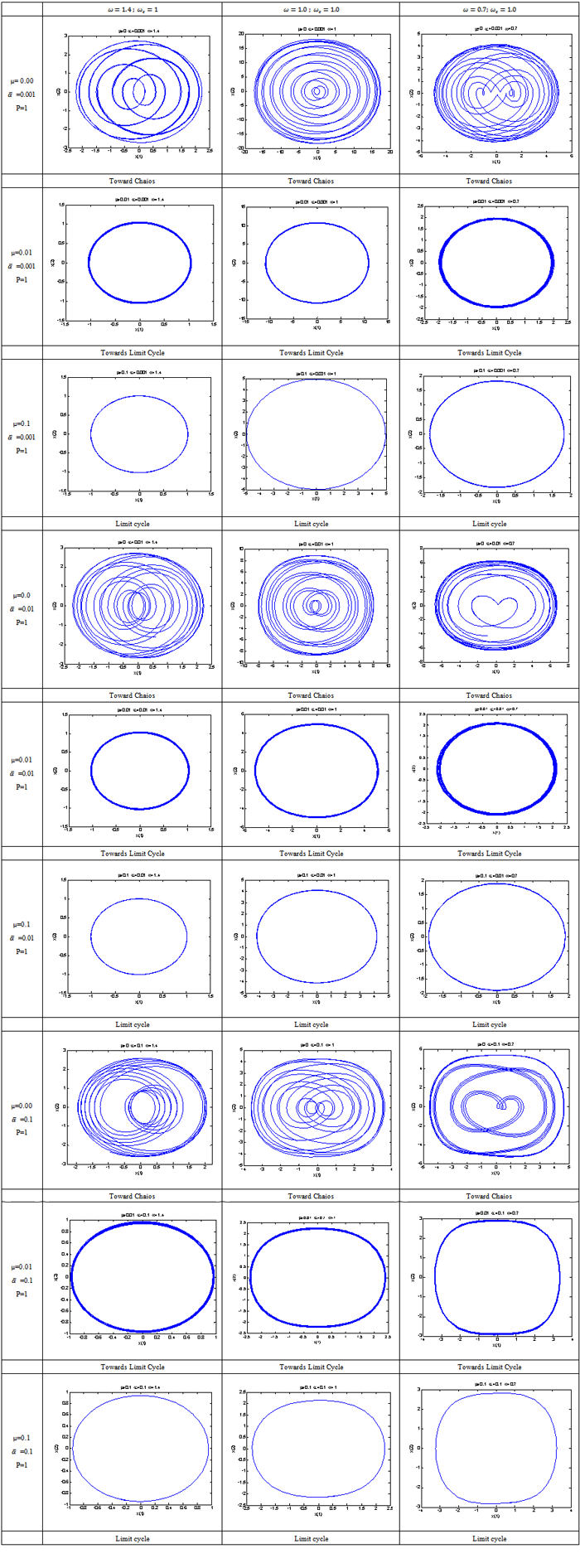
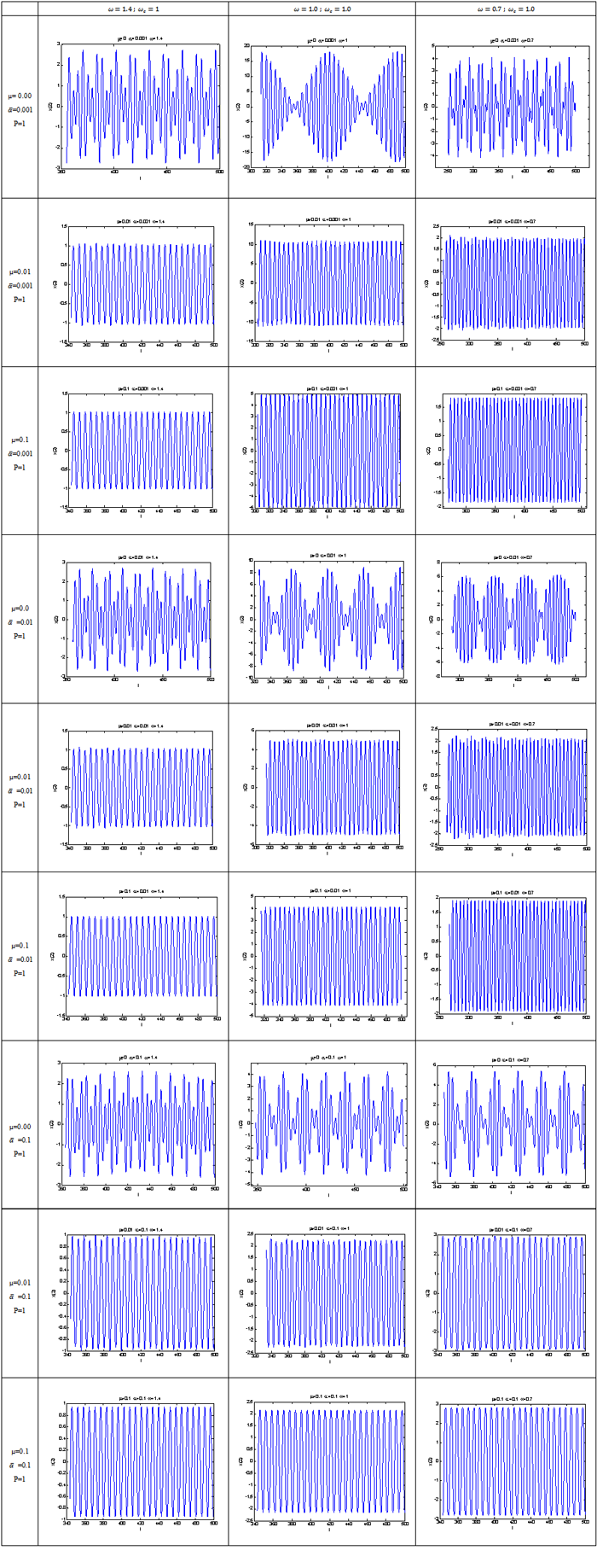
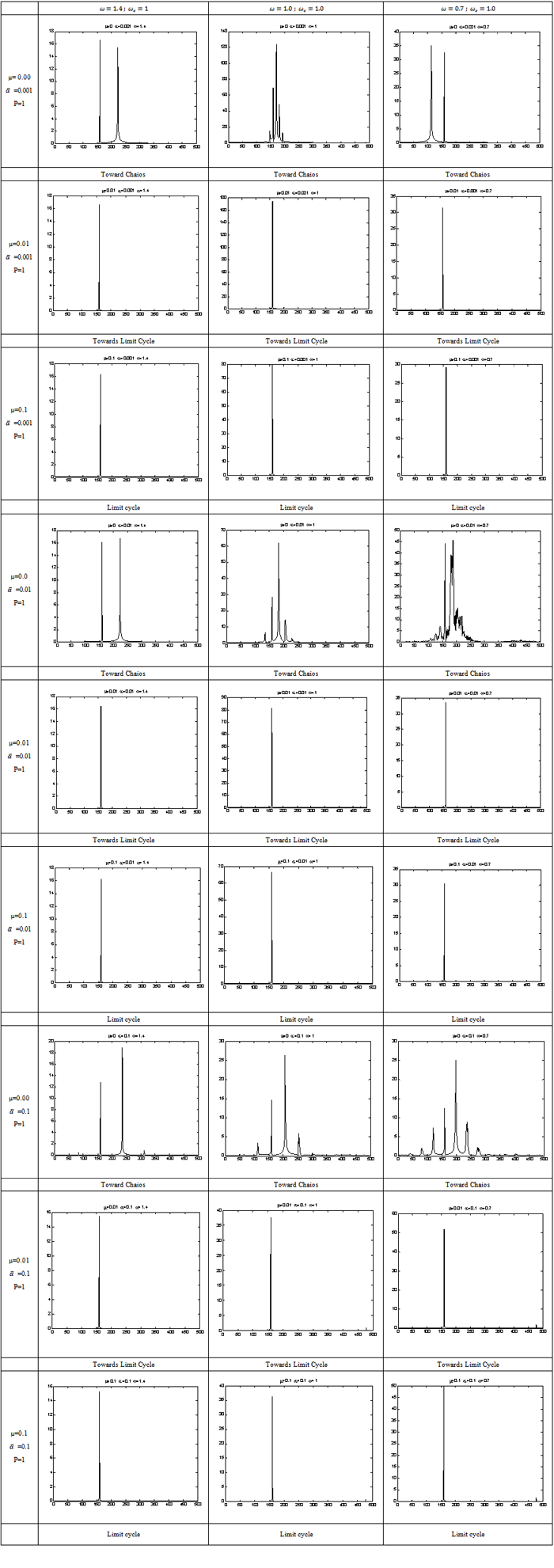
- The results for simply supported beam on elastic foundation are presented in Figures 2 through 6, Table 1 and Table 2. Figures 2 through 6 present the results of the linearized model whereas Table 1, 2 and 3 represent the results of the nonlinear model. Figure 2 present the linear system behavior for µ>0 and ∆≥0. It is obvious that the system is stable attractive node. Table 1 represents sample phase diagrams of the studied ranges. Figure 3 shows stable centre for the linear system of µ=0 and ∆≥0. Figure 4 presents stable spiral for the linear system behavior of µ>0 and ∆<0. In Figures 2, 3 and 4 the system is stable however in Figures 5 and 6 it is not stable. The behavior in both Figures 5 and 6 is unstable node. Table 2 shows the time response for those cases that are presented in Table 1, whereas the corresponding frequency spectra (Fast Fourier Transform-FFT) for those cases presented in both Tables 1 and 2. The phase portraits and the time response are collected after long period of time to be sure that the system has passed the transient range. The duffing Equation (16) is converted into system of first order ordinary differential equation as shown in Equation (17) and solved using MATLAB package by utilizing the Runga-Kutta ODE (Ordinary Differential Equation) solver. The equation which represents the system under investigation is of cubic nonlinearity with harmonic excitation.The sample results present the effect of damping when the system has weak, medium and strong nonlinearity for excitation frequencies below, at and above resonance. The whole study is considering weak nonlinearity that does not exceed
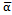 =0.1 and those levels of weak, medium and strong within that range. Only the first mode is considered in this study. The parameters range covered in this investigation are for μ=0.0 through 0.1,
=0.1 and those levels of weak, medium and strong within that range. Only the first mode is considered in this study. The parameters range covered in this investigation are for μ=0.0 through 0.1,  = 0.001 through 0.1 and natural frequency 𝜔= 0.7 through 1.4. It can be seen from Table 1 that when there is no damping the system is tending toward chaos however when little damping is applied the system is tending towards limit cycle.It is obvious that the damping and the nonlinearity are the most effective parameters in controlling the chaotic behavior of the system. As long as the radius of gyration for the beam under consideration is large i.e., the beam is more towards slender, the nonlinearity is going to be weak. This means that the contribution of the stretching energy to the behavior of the system is going to be low. The damping system dissipates the oscillating energy and provides a control over the system behavior. For the linear system, as long as damping coefficient is positive, the transient response is going to decrease exponentially and the forcing excitation response is bounded even at resonance. For undamped linear system the forcing excitation response is not bounded and the response is increasing with time. For the nonlinear system, the response is tending toward chaos as it can be seen in Table 1 for μ=0.0. However when the damping increases the system is transferring from chaos to limit cycle. It is obvious in Table 3 that all cases of μ=0.0 have Double period, Triple period, or, Chaotic response. The response of those double period cases shows amplitude modulation whereas those cases where their frequencies are very close show beating phenomenon. For the resonance case of no damping i.e., the excitation frequency equals the natural frequency, the linear system has increasing amplitude response whereas the nonlinear system is tending towards chaos with bounded amplitude. It is obvious that the nonlinear cases (within the range of investigation) are tending towards chaos as long as there is no damping in the system.
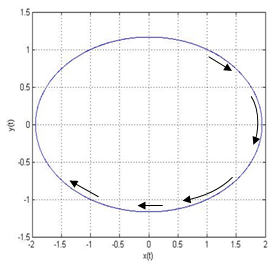
= 0.001 through 0.1 and natural frequency 𝜔= 0.7 through 1.4. It can be seen from Table 1 that when there is no damping the system is tending toward chaos however when little damping is applied the system is tending towards limit cycle.It is obvious that the damping and the nonlinearity are the most effective parameters in controlling the chaotic behavior of the system. As long as the radius of gyration for the beam under consideration is large i.e., the beam is more towards slender, the nonlinearity is going to be weak. This means that the contribution of the stretching energy to the behavior of the system is going to be low. The damping system dissipates the oscillating energy and provides a control over the system behavior. For the linear system, as long as damping coefficient is positive, the transient response is going to decrease exponentially and the forcing excitation response is bounded even at resonance. For undamped linear system the forcing excitation response is not bounded and the response is increasing with time. For the nonlinear system, the response is tending toward chaos as it can be seen in Table 1 for μ=0.0. However when the damping increases the system is transferring from chaos to limit cycle. It is obvious in Table 3 that all cases of μ=0.0 have Double period, Triple period, or, Chaotic response. The response of those double period cases shows amplitude modulation whereas those cases where their frequencies are very close show beating phenomenon. For the resonance case of no damping i.e., the excitation frequency equals the natural frequency, the linear system has increasing amplitude response whereas the nonlinear system is tending towards chaos with bounded amplitude. It is obvious that the nonlinear cases (within the range of investigation) are tending towards chaos as long as there is no damping in the system.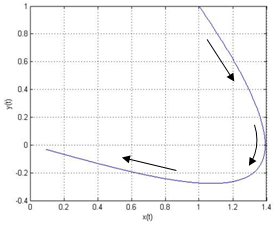 | Figure 2. Presentation of the linear system behavior for µ>0 and ∆≥0. Where µ=0.7,ω=0.6, 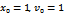 . The system is a stable, attractive node . The system is a stable, attractive node |
 | Figure 3. Presentation of the linear system behavior for µ=0 and ∆≥0. Where µ=0 ω=0.6 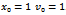 . The system is a stable center . The system is a stable center |
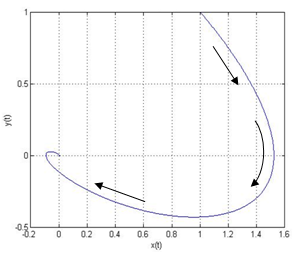 | Figure 4. Presentation of the linear system behavior for µ>0 and ∆<0. Where µ=0.4 ω=0.6 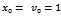 , The system is a stable spiral point , The system is a stable spiral point |
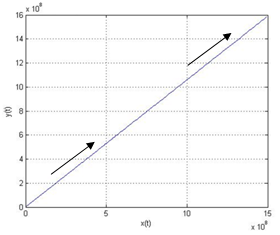 | Figure 5. Presentation of the linear system behavior for µ<0 and ∆≥0. Where µ=-0.7 ω=0.6 , The system is an unstable node |
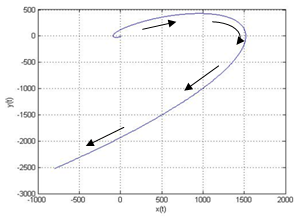 | Figure 6. Presentation of the linear system behavior for µ<0 and ∆<0. Where µ=-0.4 ω=0.6 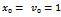 , The system is an unstable node , The system is an unstable node |
|
|
|
5. Conclusions
- The behavior of nonlinear beam on elastic foundation is unveiled. It is found that the system is stable and controllable as long as the damping coefficient is non zero and positive. As the nonlinearity increases more damping is required to prevent it from moving towards chaos. For first mode shape the natural frequency could be calculated as square root of the sum of squares of both natural frequency of the beam and the foundation. The strength of the nonlinearity is inversely proportional to the square of the radius of gyration, i.e. as long as the beam more towards slender the nonlinearity is weaker. The stretching potential energy is responsible for generating the cubic nonlinearity in the system.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML