-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2012; 2(2): 25-35
doi:10.5923/j.jmea.20120202.05
A Cellular-rearranging of Population in Genetic Algorithms to Solve Assembly-Line Balancing Problem
Hossein Rajabalipour Cheshmehgaz1, Mohammd Ishak Desa1, Farahnaz Kazemipour2
1Faculty of Computer Science and Information Systems, Universiti Teknologi Malaysia, Skudai, 81310, Johor, Malaysia
2Faculty of Management and Human Resources Development, Universiti Teknologi Malaysia, Skudai, 81310, Johor, Malaysia
Correspondence to: Hossein Rajabalipour Cheshmehgaz, Faculty of Computer Science and Information Systems, Universiti Teknologi Malaysia, Skudai, 81310, Johor, Malaysia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Assembly line balancing problem (ALBP) is the allocating of assembly tasks to workstations with consideration of some criteria such as time and the number of workstations. Due to the complexity of ALB, finding the optimum solutions in terms of the number of workstations in the assembly line needs suitable meta-heuristic techniques. Genetic algorithms have been used to a large extent. Due to converging to the local optimal solutions to the most genetic algorithms, the balanced exploration of the new area of search space and exploitation of good solutions by this kind of algorithms as a good way can be sharpened with some meta-heuristic. In this paper, the modified cellular (grid) rearranging-population structure is developed. The individuals of the population are located on cells according to the hamming distance value among individuals as neighbours before regenerations and a family of cellular genetic algorithms (CGAs) is defined. By using the cellular structure and the rearrangements, some of the family members can find better solutions compared with others in the same iterations, and they behave much more reasonably in order to acquire the solution in terms of the number of workstations and the smoothly balanced task assignment on criteria conditions.
Keywords: Cellular Genetic Algorithms, Assembly-line Balancing, Hamming Distance
Cite this paper: Hossein Rajabalipour Cheshmehgaz, Mohammd Ishak Desa, Farahnaz Kazemipour, A Cellular-rearranging of Population in Genetic Algorithms to Solve Assembly-Line Balancing Problem, Journal of Mechanical Engineering and Automation, Vol. 2 No. 2, 2012, pp. 25-35. doi: 10.5923/j.jmea.20120202.05.
Article Outline
1. Introduction
- From ancient times to the modern day, assembly lines (ALs) have been modified as long as the long-term optimal design of the lines has surely been the most important milestone in the manufacturing process. Whereas designer of ALs (mostly) deal with many assembly tasks (around 400 tasks in a typical car ALs) and some critical limitations in design, the optimal solution can be achieved via a variety of heuristic ideas that must be massively computerized. Most of the work related to ALs concentrates on the assembly-line balancing (ALB) problem. The ALB problem deals with the assignment of the tasks (as duties) among workstations (or operators) so that the precedence relations are not violated, the total time for tasks in each workstation does not exceed the cycle time and a given objective function is considered to be optimized. The ALB problem falls into the NP-hard class of combinatorial optimization problems[1]. If there are n tasks and r preference constraints, then there are n!/2r possible task sequences[2]. Therefore, it can be time consuming for optimum-seeking methods to gain an optimal solution within this extremely large search space for some manufacturing operations, such as car assembly lines with more than 100 workstations. Despite the vast search space, many studies have tried to solve the ALB problem using optimum-seeking methods, such as linear programming [e.g. 3], integer programming [e.g. 4], dynamic programming [e.g. 5] and branch- and- bound approaches [e.g. 6]. However, none of these methods has proven to be of practical use for large assembly lines due to their computational inefficiency. Hence, the next research efforts have been directed towards the development of heuristics [e.g. 7, 8] and meta-heuristics such as simulated annealing [e.g. 9], tabu search [e.g. 10] and genetic algorithms [e.g. 11].Due to the complexity of the ALB problem, a growing number of researchers have employed genetic algorithms (GAs), and most industrial engineers also use them to optimize problems which are difficult to find an optimal solution for in a reasonable time. GAs provides an alternative to traditional optimization techniques by using directed random searches to locate optimum solutions in complex search spaces. Hence, because of the popularity of GAs’ application to the ALB problem, some papers exist which review the subject, including Dimopoulos and Zalzala[12], Scholl and Becker[13] and Tasan and Tunali[14] have all tried to modify GA using modified selection techniques, individual representation, crossover techniques etc. in order to improve the algorithms.As having different priorities and objectives that GAs are trying to optimize as fitness functions, the ALB problem can be classified into some classes with different objectives. Additionally, the GAs’ setting in chromosomes representations, initial population, and operation mechanisms were considered by GA designers to be like challenge and benchmarking.
1.1. ALB Problem Classes and their Objectives
- Before making any decisions about assembly line design, the ALB problem must be classified according to the objectives and what needs to be developed. Figure 1 illustrates the classification of ALBP based on the objective function and problem structure[2,13,15-16].
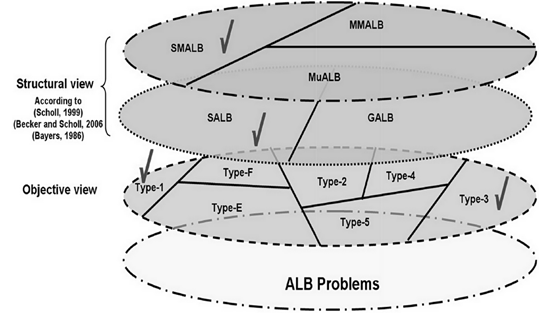 | Figure 1. Classification of assembly line balancing problems and our research boundaries |
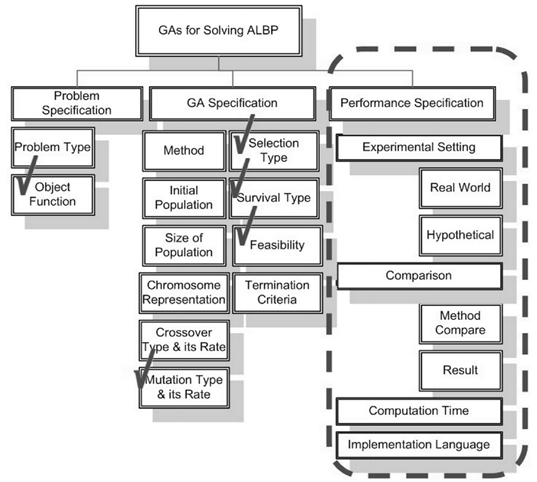 | Figure 2. GAs Parameters and setting for ALBPs- sources:[14] |
2. Typical Genetic Algorithms for ALB
- The structure of typical GA (TGA) is explained below as it performs one generation initial population, crossover and mutation operation in iteration. Generate initial population RepeatChoose two individuals as parents for recombinationApply crossover with Rc probability Apply mutation with Rm probability Replace parents with offspringUntil stopping condition is reachedTake the best chromosome of the population as the solutionGA specification is an initial step. Following subsections introduce task-based representation, initial population and crossover operation as long as new fitness function and mutation technique are introduced.
2.1. Representation
- Sabuncuoglu et al.[19] has introduced task-based representation (TBR) where each task is represented by a number that is placed on a string (i.e. individual) with the string size equal to the number of tasks. The tasks are ordered by the individual relative to their order of processing. The tasks are allocated to workstations so that the sum of the task times in each station does not exceed the cycle time. This coding scheme is demonstrated in Figure 3 through a 7-task problem example as follows.Example: we have seven tasks with own times shown in Figure 3.a, the precedence graph (matrix) are presented in Figure 3.b and the cycle time is equal to 20. Figure 3.c illustrates a string with an order of tasks that means tasks 1, task3 and task 2 are assigned to workstation 1, tasks 4, 5 and 6 are assigned to workstation 2 and finally task 7 is allocated to workstation 3. Figure 3.d shows another configuration for the task balancing equaled with the string representation that is illustrated in Figure 3.e.
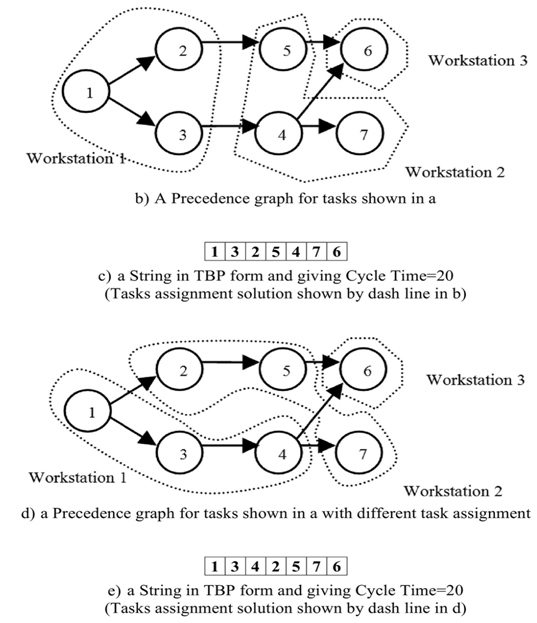 | Figure 3. An example shows Task-Base Representation for two different optimum solutions |
2.2. Objectives and Fitness Function Definition
- There are many solutions for ALB but a few of them are better than others based on some objectives. However, the important objective of the ALB problem is to minimize the number of workstations but, in practical view, the balancing algorithm should also balance the total idle times among workstations too and provide a smooth balanced solution. In the previous example, the first configuration of task balancing, Figure 3.b, needs 3 workstations. The first workstation has tasks with total time: 5+5+9=19. The second workstation with total task time: 4+6+9, needs 19 units of time, and the third workstation needs 20 units of time. In the second configuration, Figure 3.d, the first workstation needs 18 units of time, the second one needs 20 and the third one needs 20 units of time. Although the total idle times for both cases is the same and equal to 2 units of time, the first configuration is more smoothly balanced based on idle time than the second. Hence, we have defined a utility function for fitness function that consists of two objectives, i.e. minimizing the number of workstations and maximizing smoothness among workstations. The given and decision variables are introduced as follows.Parameters:
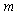 : Number of tasks in AL (a given variable)
: Number of tasks in AL (a given variable)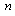 : Number of needed workstations (a decision variable)
: Number of needed workstations (a decision variable)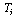 : Task identity
: Task identity 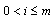
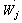 : Workstation identity
: Workstation identity 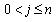
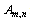 : A binary matrix where its rows indicate the tasks and its columns indicate the workstations:
: A binary matrix where its rows indicate the tasks and its columns indicate the workstations: 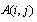 ’s value is 1 or 0. The value of 1 means that task
’s value is 1 or 0. The value of 1 means that task 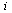 is assigned to workstation number
is assigned to workstation number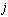 and 0 means not (a decision variable)
and 0 means not (a decision variable)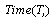 :
: 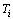 time (units of time) (a given variable)
time (units of time) (a given variable)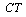 : Cycle time in AL(a given variable)
: Cycle time in AL(a given variable)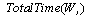 : Total time the workstation
: Total time the workstation 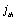 is busy,
is busy, 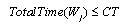 (a decision variable)
(a decision variable)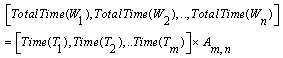 | (1) |
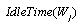 : Idle time in workstation
: Idle time in workstation 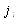 th, (a decision variable)
th, (a decision variable)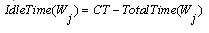 | (2) |
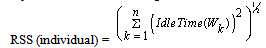 | (3) |
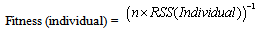 | (4) |
 . Equation (2) specifies the idle time left in each workstation. Equation (3) illustrates a measure of balance and smoothness in the line by a solution and Equation (4) specifies the fitness value of a solution (used in this research).
. Equation (2) specifies the idle time left in each workstation. Equation (3) illustrates a measure of balance and smoothness in the line by a solution and Equation (4) specifies the fitness value of a solution (used in this research).2.3. Initial Population
- The initial population is generated randomly assuring feasibility according to precedence relations. So, all individuals in the population in all generational steps will be feasible.
2.4. Crossover Technique
- The two parents that are selected are cut at two random cut-points. The offspring takes the same genes outside the cut-points at the same location as its parent and the genes in between the cut-points are scrambled according to the order that they have in the other parent. Sabuncuoglu et al.[19] presented the applicable crossover technique that we follow. It is demonstrated in Figure 4. The major reason that makes the crossover operator important is that it assures feasibility of the offspring. Since both parents are feasible, both children must also be feasible. Keeping a feasible population is a key to the ALB problem since preserving feasibility drastically reduces computational effort.
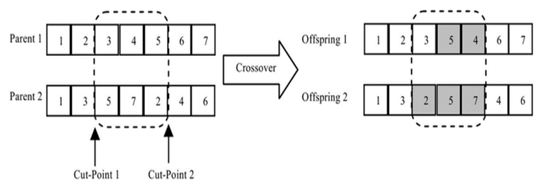 | Figure 4. The crossover operation (gained from Sabuncuoglu et al., 2000) |
2.5. Mutation Technique
- In the mutation operation, a cut-point is randomly selected and the gene (bit) in this point is replaced with next gene (right-side) if it is possible (according to precedence limitations) and then all following genes will be exchanged to right-side gen as the same till there is no possibility to exchange. Figure 5 shows one mutation in the individual shown in Figure 3.e. As it is obvious, due to feasibility, gene 4 can be replaced with gene 2 and then with 5 till it cannot be exchanged.
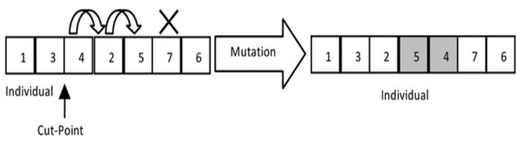 | Figure 5. The mutation operation |
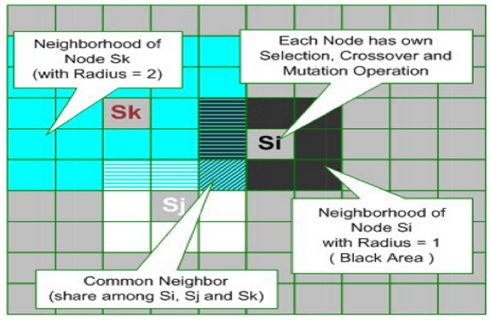 | Figure 6. A 2-dimensional grid (cellular) structure with 3 nodes (cells) with different radius (1 and 2) and their neighbours |
3. Cellular-Rearranging of Population
3.1. Cellular (grid) Structure
- The cellular structure (CS) used in this paper is a simplified version of cellular automaton (CA). CA is a collection of cells (nodes) on a grid of a specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells. The rules are then applied iteratively for as many time steps as desired. Von Neumann is one of the first people to consider such a model, and incorporated a cellular model into his ‘universal constructor’ Cellular automata were studied in the early 1950s as a possible model for biological systems[30]. In this paper terminology, a CS comprises three components:
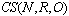 which is explained below.● N: size of CS (for instance,
which is explained below.● N: size of CS (for instance, 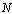 =10 means a grid with 10*10 nodes – Figure 6 shows a 10*10 CS).● R: radius of neighborhoods (figure 6 shows the two different radiuses with 1 and 2 – but in one CS, a unique radius amount must be used).● O: a set of rules in each node and can be done simultaneously and separately.The rules specify the states of nodes in the next time step. The state of node can be Boolean as active or inactive, or be a digit number, or even be binary strings. Let
=10 means a grid with 10*10 nodes – Figure 6 shows a 10*10 CS).● R: radius of neighborhoods (figure 6 shows the two different radiuses with 1 and 2 – but in one CS, a unique radius amount must be used).● O: a set of rules in each node and can be done simultaneously and separately.The rules specify the states of nodes in the next time step. The state of node can be Boolean as active or inactive, or be a digit number, or even be binary strings. Let 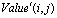 show the state of a node with location in
show the state of a node with location in 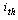 row and
row and 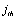 column in CS at time
column in CS at time 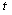 and
and 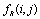 is a rule function that depends on the values of all nodes around node
is a rule function that depends on the values of all nodes around node 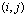 and the neighbourhood with radius
and the neighbourhood with radius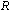 and one can calculate the value of the node in the next time step. Equation (5) illustrates that
and one can calculate the value of the node in the next time step. Equation (5) illustrates that 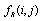 is calculated by function
is calculated by function 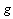 which depends on all values of neighbors in the previous time step.
which depends on all values of neighbors in the previous time step.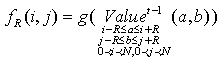 | (5) |
3.2. Cellular Genetic Algorithms (CGA)
- Sivanandam and Deepa[31] have classified GAs into five groups: simple GA, parallel & distributed GA, master-slave GA, coarse grained GA, and cellular GA. In the last group, the grid or fine-grained model individuals are placed on a large doughnut-shaped (the ends wrap around) one- or two-dimensional grid, one individual per grid location. The model is also called cellular because of its similarity with cellular automata with stochastic transition rules. Fitness evaluation is done simultaneously for all individuals and selection, reproduction and mating takes place locally within a small neighborhood. In time, semi-isolated niches of genetically homogeneous individuals emerge across the grid as a result of slow individual diffusion. This phenomenon is called isolation by distance and is due to the fact that the probability of interaction of two individuals is a fast decaying function of their distance. Recently Alba and Dorronsoro[32] have surveyed all conditions in CGA as a completed survey.The following is a conventional the cellular genetic algorithmic (
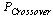 and
and 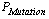 are the parameters which show the probability of performing crossover and mutation operations set by a GA designer)[31-32]:Generate a random individual j (feasible solution)End parallel forWhile not termination condition doFor each cell j do in parallelEvaluate individual j (fitness function calculation)Select a neighboring individual kProduce offspring from j and k with probability
are the parameters which show the probability of performing crossover and mutation operations set by a GA designer)[31-32]:Generate a random individual j (feasible solution)End parallel forWhile not termination condition doFor each cell j do in parallelEvaluate individual j (fitness function calculation)Select a neighboring individual kProduce offspring from j and k with probability 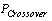 Mutate j with probability
Mutate j with probability 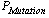 Assign one of the best offspring to jEnd parallel forEnd whileIn a more sophisticated view of CGAs, the new capsulated definition is presented. The capsulated definition helps to understand GAs in CS. First, the nodes must comprise two parts of information saved in the nodes in two successive time steps:
Assign one of the best offspring to jEnd parallel forEnd whileIn a more sophisticated view of CGAs, the new capsulated definition is presented. The capsulated definition helps to understand GAs in CS. First, the nodes must comprise two parts of information saved in the nodes in two successive time steps: 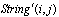 and
and 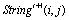 illustrate the genetic individuals (string/chromosome) at time steps
illustrate the genetic individuals (string/chromosome) at time steps 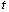 and
and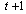 ; and
; and 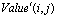 and
and 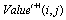 are as previously defined in Section 3.1, but in two successive time steps. Secondly, the rule that calculating the values of the nodes comprises all genetic operation- selection, crossover and mutation - at once. The following pseudo codes show the modified rule function components and their order according to the genetic algorithms steps.
are as previously defined in Section 3.1, but in two successive time steps. Secondly, the rule that calculating the values of the nodes comprises all genetic operation- selection, crossover and mutation - at once. The following pseudo codes show the modified rule function components and their order according to the genetic algorithms steps. 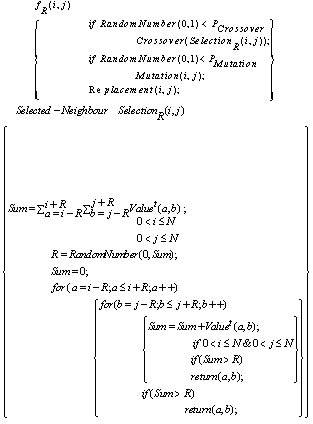
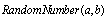 function generates a random number between a and b, and
function generates a random number between a and b, and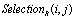 works by a local selection mechanism and neighborhood; radius
works by a local selection mechanism and neighborhood; radius 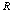 reveals a location of the neighbor which has already been selected for crossover operation in node
reveals a location of the neighbor which has already been selected for crossover operation in node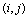 . Fitness proportionate selection, also known as the roulette-wheel selection method, is employed by
. Fitness proportionate selection, also known as the roulette-wheel selection method, is employed by 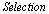 operation[33]. The crossover and mutation operations that are mentioned in the pseudo code work as they are designed in TGA locally (see Section 2). An issue in CGA is elitism strategy which means the best individuals in the old population should survive to the next population. Due to local selection in CGA, it cannot apply the strategy directly. In the final steps of CGA, replacement is considered and the best string (individual) among offspring based on fitness value would be a substitute for the old individual in node. The
operation[33]. The crossover and mutation operations that are mentioned in the pseudo code work as they are designed in TGA locally (see Section 2). An issue in CGA is elitism strategy which means the best individuals in the old population should survive to the next population. Due to local selection in CGA, it cannot apply the strategy directly. In the final steps of CGA, replacement is considered and the best string (individual) among offspring based on fitness value would be a substitute for the old individual in node. The 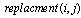 function replaces the old value in the node with the best value gained from the last two time steps (see pseudo code following). And the value of individual fitness that is saved as
function replaces the old value in the node with the best value gained from the last two time steps (see pseudo code following). And the value of individual fitness that is saved as 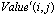 in the node must be calculated again by
in the node must be calculated again by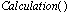 .
. In this paper, there are also some modifications in CGA as follows.
In this paper, there are also some modifications in CGA as follows.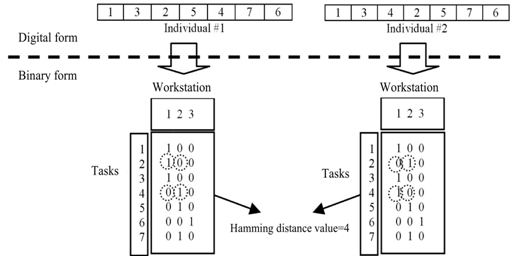 | Figure 7. Transfer process to binary form and hamming distance calculation |
3.3. Hamming distance (HD)
- Making the selection operation restricted is well-known strategy to prevent genetic drifting[34]. The grid structure can be usefully used to make the restriction[32]. In order to have a variety mates to be selected by individuals, in this research, the hamming distance parameter is considered specifying the similarity value among individuals. Each individual might be transferred to binary form as the assignment matrix (see Figure 7 – the columns specify the workstations number and the rows specify the tasks number in the assignment matrix, and the ‘1’ or ‘0’ symbol in each element illustrates which task is or is not assigned to which workstation) and then the value of the hamming distance can be calculated by counting the different 0s and 1s in genotype of individuals. Figure 7 illustrates the transfer process from phenotype (digital) form (task-based representation) to genotype (binary) form (assignment matrix) and the concept of similarity between individuals by using the hamming distance value. The example (in Figure 7) shows the value of
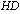 between individual #1 and #2 is 4 or, in another definition,
between individual #1 and #2 is 4 or, in another definition, 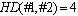 .It is assumed that if mates are similar (or dissimilar) to each other they would be better parents to make offspring. To put this idea to the test, some steps in CGA need to be modified. The next subsection shows a new change in CGA in the new step, ‘cellular rearrangement’ and it seems to work like pre-processing before doing any genetic operation in each generation or frequently.
.It is assumed that if mates are similar (or dissimilar) to each other they would be better parents to make offspring. To put this idea to the test, some steps in CGA need to be modified. The next subsection shows a new change in CGA in the new step, ‘cellular rearrangement’ and it seems to work like pre-processing before doing any genetic operation in each generation or frequently.3.4. Rearrangements and CGA family
- Some kinds of arrangement are selected to locate the individual on a grid’s nodes. By the arrangements we try to test the effectiveness of making the neighborhood. For instance, what if one individual could have a greater chance to have crossover with another individual that is so similar to or different to it.In this research, three kinds of arrangements techniques are used: max-hamming distance, min-hamming distance and max-min-hamming distance, and then all are mixed with CGA as an added step and make the CGA family (Figure 8 shows the new framework of the CGA family).
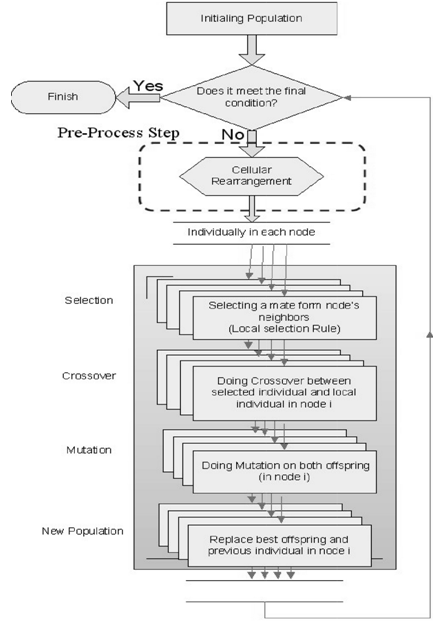 | Figure 8. Flowchart Abstract of CGA Family |
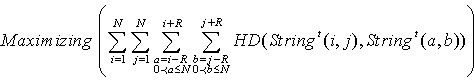 | (6) |
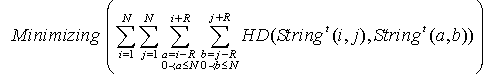 | (7) |
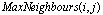 represent a set of all the neighbors around node
represent a set of all the neighbors around node  that are supposed to have maximum hamming distance valued with the individual allocated in node
that are supposed to have maximum hamming distance valued with the individual allocated in node , and
, and 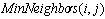 embody a set of the neighbors who are supposed to have minimum hamming distance value with the individual in node
embody a set of the neighbors who are supposed to have minimum hamming distance value with the individual in node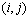 . The objective of rearrangement in MMHCGA can be presented by two formulations (8) and (8).
. The objective of rearrangement in MMHCGA can be presented by two formulations (8) and (8).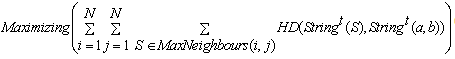 | (8) |
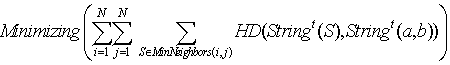 | (9) |
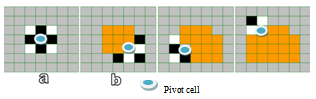 | Figure 9. Initial four steps of MMHCGA Rearrangement. |
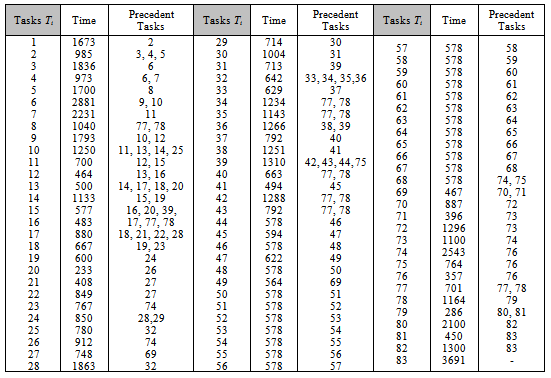
4. Simulation and Results
- To analyse the CGA algorithms family, a case with 83 assembly tasks were selected [from 29]. The given cycle time for all workstations is 5000 units of time. To make the results quite clear and also finding the differences between the CGA family and typical (ordinary non-cellular) GA, the following parameters values were fixed, but the values could be changed to different values also.The time of each task has been shown in Table 1. Each algorithm executed from the initial population created randomly, by 100 executions with 300 iterations in each. The best individual and the worst individual (based on fitness value) in new populations generated by the algorithms, were recorded at the end of iterations of 10, 20, 30… and 300. And the average fitness value at the end of the iterations for all CGA family algorithms were also calculated and recorded. An individual that has used the minimum number of workstations and has minimal RSS (root sum square) of idle times was identified as a relative best task balancing solution here. We compared the all member of CGA family with each other and the typical GA (TGA) on these circumstances.As the GA parameters part involved, to set the parameters for GA, the selection rule that is used is the roulette selection technique, and other parameters are fixed as follows.Genetic parameters setting:● Population size: 100● Selection rule: roulette wheel selection● Crossover rate: 0.9● Mutation rate: 0.2● Elitism rate: 0.05 (only for TGA)● Iteration (reproduction of population) number: 300● Number of Executions (for sampling): 100As mentioned before, the best solution would be the one (set of) individual(s) that has(have) minimum number of workstation (that it needs) and minimum RSS of idle times (maximum smoothness of tasks) by giving CT=5000.
|
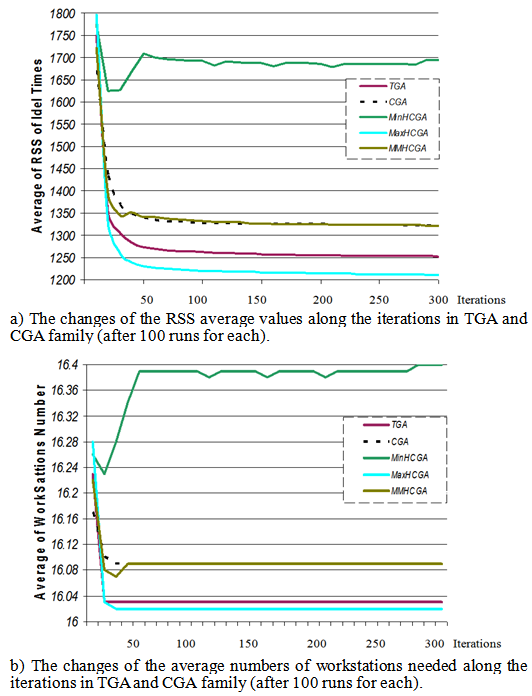 | Figure 10. CGS family behaviors in different iterations (on average values of RSS and needed workstations number basis) |
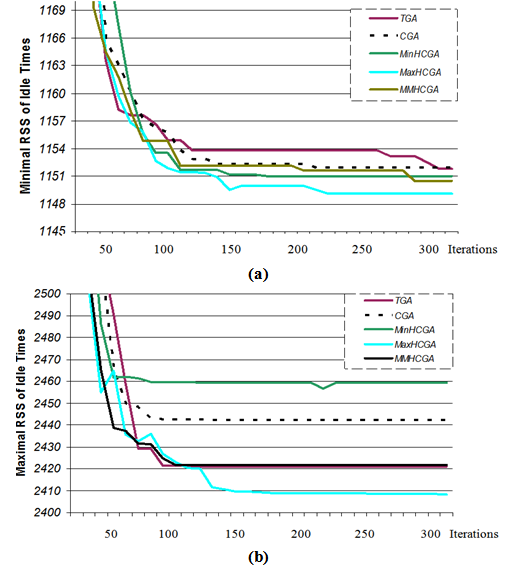 | Figure 11. CGS Family behaviors in different iterations (on minimum and maximum value of RSS basis) |
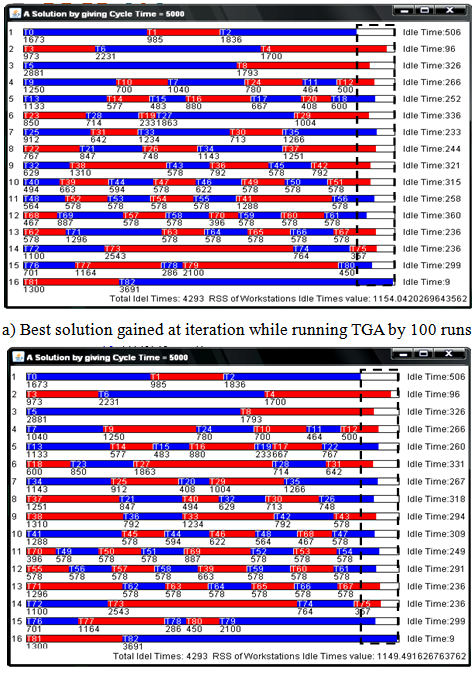 | Figure 12. Two best solutions of MaxHCGA and TGA by iteration 100. |
5. Conclusions
- Although two conventional criteria; minimum workstations and idle times, were considered here, other pragmatic criteria such as material handling constraints, resource limitations, human factors and multiple or mixed-model assembly manufacturing issues can be considered as further research directions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML