Abdullah H. M. AlEssa 1, 2
1Department of Mechanical Engineering, Engineering Faculty, Northern Borders University, Arar, Kingdom of Saudi Arabia
2Al-Balqa Applied University, Al-Huson University College, Al-Huson - Irbid , P. O. Box 50, Jordan
Correspondence to: Abdullah H. M. AlEssa , Department of Mechanical Engineering, Engineering Faculty, Northern Borders University, Arar, Kingdom of Saudi Arabia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This study examined heat transfer enhancement from a horizontal rectangular fin embedded with square perforations under natural convection compared to the equivalent solid (non perforated) fin. The parameters considered were geometrical dimensions and thermal properties of the fin and of the perforations. The study considered the gain in fin area and extent of heat transfer enhancement due to perforations. It showed also that for certain range of square dimension and spaces between perforations there is an improvement in perforated fin heat dissipation over that of the equivalent solid one. The heat transfer enhancement of the perforated fin increases as the fin thickness is increased.
Keywords:
Finite Element technique, Perforated Fin, Heat Dissipation, Heat transfer enhancement, Natural convection
1. Introduction
The removal of excess heat from system components is essential to avoid damaging effects of overheating. Therefore, the enhancement of heat transfer is an important subject of thermal engineering. The heat transfer from surfaces may in general be enhanced by increasing the heat transfer coefficient between a surface and its surroundings, by increasing the heat transfer area of the surface, or by both. In most cases, the area of heat transfer is increased by utilizing extended surfaces in the form of fins attached to walls and surfaces[1].Fins as heat transfer enhancement devices have been quite common. As the extended surface technology continues to grow, new design ideas emerge including fins made of anisotropic composites, porous media, and interrupted plates[1, 2, 3]. Due the high demand for lightweight, compact, and economical fins, the optimization of fin size is of great importance. Therefore, fins must be designed to achieve maximum heat removal with minimum material expenditure taking into account, however, the ease of manufacturing of the fin shape[4-6].Large number of studies has been conducted on optimizing fin shapes. Other studies have introduced shape modifications by cutting some material from fins to make cavities, holes, slots, grooves, or channels through the fin body to increase the heat transfer area and/or coefficient[5-8]. One popular heat transfer augmentation technique involves the use of rough surfaces of different configurations. The surface roughness aims at promoting surface turbulence that is in te-nded mainly to increase the heat transfer coefficient rather than the surface area[1, 7, 9]. It was reported that non-flat surfaces have free convection coefficients that are 50% to 100% more than those of flat surfaces[1, 9]. Several other researchers reported a similar trend for interrupted (perforated) fins attributing the improvement to the restarting of the thermal boundary layer after each interruption indicating that the increase in convection coefficient is even more than enough to offsets lost area, if any[1].Perforated plates (fins) represent an example of surface interruption[1, 7, 8] and are widely used in different heat exchanger, film cooling, and solar collector applications. Despite the fact that correlations for the convection coefficient within cavities and over the surfaces of non-perforated plates are readily available[1, 9, 10], literature search indicated a lack of such relations for the perforated surfaces under natural convection. Consequently, surface coefficients were estimated based on the concepts of augmentation ratio and open area ratio[1, 2].This study aims mainly at examining the extent of heat transfer enhancement from a horizontal rectangular fin under natural convection conditions as a result of introducing surface modifications (interruptions) to the fin. The modifications in this work are vertical rectangular perforations made through the fin thickness. The study investigates the influence of perforations on heat transfer rate or heat dissipation rate of the perforated fin. The modified fin, called perforated fin, is compared to the corresponding solid (non-perforated) fin in terms of heat transfer rate. The study eventually attempts to make the best use of the material and size of a given fin, which involves some sort of optimization. The overall objective of this study was to evaluate the potential of heat transfer enhancement when body perforations of square cross section are introduced to a horizontal rectangular fin under natural convection conditions. The specific objectives of the work may be summarized as follows:1. Evaluate the influence of relevant fin and perforation factors on the enhancement of heat transfer rate.2. Determine the values of parameters that would result in maximum heat transfer enhancement of the perforated fin compared to the solid counterpart.
2. Assumptions for Analysis
The classical treatment of fins, which assumes one-dimensional heat conduction as the Biot number is very small, that is, less than 0.01[11, 12] is considered. The perforated fin with square perforations considered in this study is shown in figure 1. Fig. For which the transverse (lateral) Biot number in (z) direction (Biz) can be calculated by (Biz = hps.t/ 2k) and the transverse Biot number in (y) direction ( Biy ) can be calculated by (Biy = hps(Sy+ b/2)/k). As the values of (Biz) and (Biy) less than .01[10, 11] then the heat transfer in (z) and (y) directions can be assumed lumped and one dimension solution can be considered. If the values of (Biz) and (Biy) greater than 0.01 then the heat transfer solution must be two or three dimensions. In this study the parameters of the perforated fin are restricted as they lead to values of (Biz) and (Biy) smaller than 0.01. The analysis and results reported are based on the following assumptions:1. Steady state one-dimension heat conduction.2. Homogeneous and isotropic fin material with constant thermal conductivity.3. No heat sources/ sinks in the fin body.4. Uniform base and ambient temperatures.5. Uniform heat transfer coefficient over the whole fin solid surface (perforated or solid)6. Uniform heat transfer coefficient within the perforation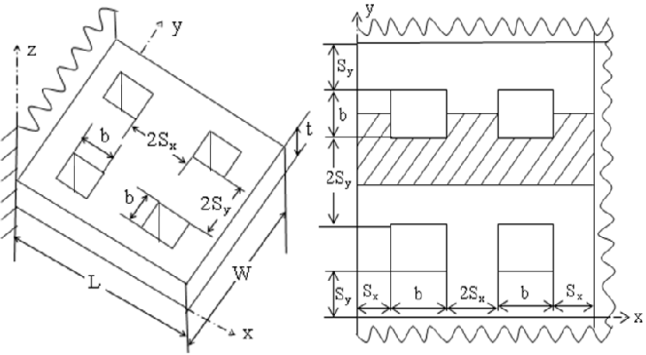 | Figure 1. The fin with square perforations and the symmetrical part (shown hatched) used in the mathematical formulation of the perforated fin |
3. Heat Transfer Analysis
Based on the above assumptions, the energy equation of the fin along with the boundary conditions may be stated as below[13]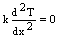 | (1) |
The associated boundary conditions are1- At the fin base (x = 0):-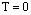 | (2) |
2- At the perforated surfaces. 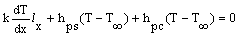 | (3) |
The fin with square perforations as it is shown in Fig. (1) is solved numerically utilizing the finite-element technique as it is described in[14]. It is established that everything else being the same, heat dissipation from a fin, solid or perforated, depends on fin surface area and heat transfer coefficients. For the solid fin, both aspects are established. The average value of hsf in natural convection is given by[9].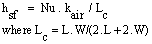 | (4) |
The average Nusselt number, Nu, is given by[9]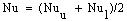 | (5) |
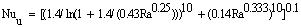 | (6) |
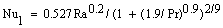 | (7) |
For the fin considered in this study, both perforated and non-perforated, the fin tip is a vertical surface for which the Nusselt number is given by[9] | (8) |
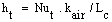 | (9) |
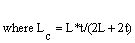 For the perforated fin there are three distinct heat transfer coefficients exist. The first one is the heat transfer coefficient of the solid portion of the perforated surfaces (hps) which can be calculated by the following expression[2]:
For the perforated fin there are three distinct heat transfer coefficients exist. The first one is the heat transfer coefficient of the solid portion of the perforated surfaces (hps) which can be calculated by the following expression[2]: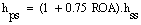 | (10) |
The second one is that the heat transfer coefficient within the perforation (hpc). Its Nusselt number (Nuc) is given by[9]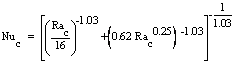 (11)The third one is that the heat transfer coefficient at fin tip (ht) which its Nusselt number (Nut) is given by equation (8). To measure the enhancement of the heat dissipation rate, it is an essential task to compare the performance of the perforated fin with that of the equivalent solid one. This can be performed by considering the ratio of heat dissipation of the perforated fin to that of the solid one (RQF) which can expressed as:
(11)The third one is that the heat transfer coefficient at fin tip (ht) which its Nusselt number (Nut) is given by equation (8). To measure the enhancement of the heat dissipation rate, it is an essential task to compare the performance of the perforated fin with that of the equivalent solid one. This can be performed by considering the ratio of heat dissipation of the perforated fin to that of the solid one (RQF) which can expressed as: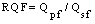 | (12) |
Where the heat dissipation of the perforated fin (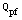 ) is computed according to the finite element heat transfer solution described in[14]. The heat dissipation of the solid fin (
) is computed according to the finite element heat transfer solution described in[14]. The heat dissipation of the solid fin (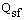 ) is computed according to the exact solution described in[15]. The material weight of the perforated fin is compared with that of the non-perforated one by weight ratio RWF which is given by:-
) is computed according to the exact solution described in[15]. The material weight of the perforated fin is compared with that of the non-perforated one by weight ratio RWF which is given by:-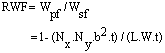 | (13) |
4. Results and Discussion
It is believed that comparing the perforated fin with its solid counterpart is the best means to evaluate the improvement or otherwise in heat transfer brought about by introducing the perforations. It is assumed that both fins have the same dimensions (the fin length is L = 50 mm and its width is W = 200 mm), same thermal conductivity, same base (Tb = 100 0C) and ambient temperatures (T∞ = 20 0C). In this study, the findings are related to heat transfer rate (heat dissipation rate). The effect of introducing the perforations on this aspect is examined by comparing the perforated fin to its solid counterpart.
4.1 Ratio of Heat Dissipation Rate (RQF)
The ratio of heat dissipation rate from the perforated fin to that of the corresponding solid one (RQF) is studied in terms of perforation dimension (b) for different values of fin thickness. The results are shown in figure (2). | Figure 2. Ratio of heat dissipation rate (RQF) vs. perforation dimension |
Figure (2) shows that thicker fins produced larger heat transfer enhancement at any b. The variation of RQF with b at various t showed a consistent trend of increasing to a maximum followed by a decrease. This trend may be explained by the net effects of changing in fin heat transfer surface area and heat transfer coefficients due to perforations. Furthermore, the figure shows that RQF is a strong function of the perforation dimension b. The perforation dimension at which RQF ratio has a maximum value is referred to as the optimum perforation dimension (bo). Figure 2 indicates that the optimum dimension (bo) is a function of the fin thickness and its thermal conductivity. The approximate values of (bo) can be obtained from figure 2.
4.2. longitudinal spacing (Sx)
To investigate the effect of longitudinal spacing (Sx) on the perforated fin performance, the heat dissipation ratio (RQF) is plotted as a function of the spacing (Sx) as shown in Fig. 3. The figure indicates that at any t, the (RQF) decreases with increasing of spacing (Sx). This behavior is due to the fact that increasing of (Sx) means smaller number of perforations, this means loss of the element that causes heat transfer enhancement. So according to (Sx) spacing it is preferable to minimize it as possible.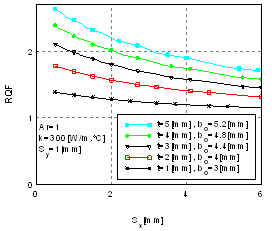 | Figure 3. Ratio of heat dissipation rate (RQF) vs. longitudinal spacing |
4.3. lateral spacing (Sy)
The effect of lateral spacing Sy on the perforated fin performance can be investigated by plotted (RQF) as a function of (Sy) for various values of thermal conductivity as shown in figure 4.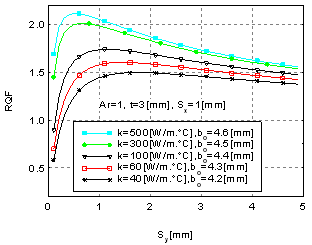 | Figure 4. Ratio of heat dissipation rate vs. lateral spacing |
The figure shows that RQF increases for low values of Sy and then tended to decline thereafter. It may be suggested here that the conflicting effects of fin thermal resistance and area are responsible for this trend. Figure 4 shows that (RQF) heavily depends on the spacing Sy. The figure indicate that (RQF) values which closely related to the optimum perforation dimension (bo) are responsive function of the spacing Sy. In this region, the ratio (RQF) attains maximum value and then decreases as the spacing Sy increases. This means that there is an optimum associated value of the spacing Sy which is abbreviated as (Syo). The values of (Syo) strongly depend on the fin thickness and its thermal conductivity. The approximate values of (Syo) can be obtained from curves like that shown in figure 4. The values of (Syo) are plotted in figure 5. This figure shows that (Syo) decreases as fin thermal conductivity and its thickness increase.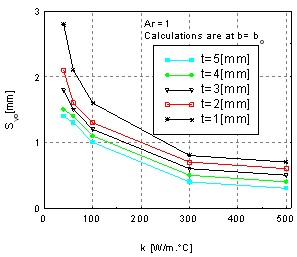 | Figure 5. Optimum lateral spacing vs. thermal conductivity |
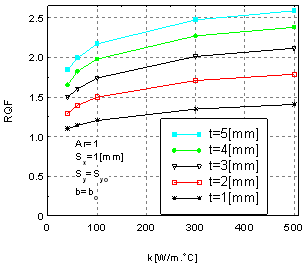 | Figure 6. RQF vs. thermal conductivity at (bo) and optimum lateral spacing (Syo) |
To summarize the advantages of using the perforated fin at the optimum values of perforation geometry, the ratios of heat dissipation (RQF) and of weight (RWF) are plotted as a function of the fin thickness with variable fin thermal conductivity at the optimum perforation dimension (bo) and optimum lateral spacing (Syo) as shown in figures 6 and 7. These figures show that the using of perforations in fins leads to enhance (augment) heat dissipation and decrease the fin weight. The enhancement increases and the weight decreases as the fin thickness and its thermal conductivity increase. This means that the using of perforated fin leads to enhance heat dissipation rates and at the same time leads to decrease the expenditure of fin material.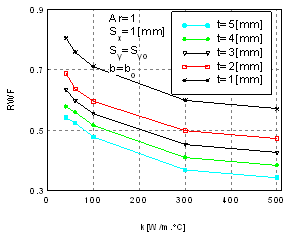 | Figure 7. RWF vs. thermal conductivity at (bo and Syo) |
5. Conclusions
1. For certain values of square perforation dimension, the perforated fin can enhance heat transfer. The magnitude of enhancement proportional to the fin thickness and its thermal conductivity..2. The extent of heat dissipation rate enhancement for perforated fins is a complicated function of the fin dimensions, the perforation geometry and the perforated fin thermophysical properties.3. The gain in heat dissipation rate for the perforated fin is a strong function of both, the perforation dimension and lateral spacing. This function attains a maximum value at given perforation dimension and spacing, which is called the optimum perforation dimension (bo), and optimum spacing (Syo), respectively.4. The perforation of fins enhances heat dissipation rates and at the same time decreases the expenditure of the fin material.
Nomenclature
A: cross sectional area of the fin Ac: cross sectional area of the perforationBi: Biot number b: square perforation dimensionh: heat transfer coefficientk: thermal conductivity of fin materialL: fin lengthl: unit vectorLc: characteristic lengthN: Number of perforations Nu: average Nusselt numberNuc: average Nusselt number of the inner perforation surface OA: open area of the perforated surface Ra: Rayleigh numberRac: Rayleigh number of the perforation inner lining surfaceROA: ratio of open areaRQF: Ratio of heat dissipation rate of perforated fin to that of non-perforated finRWF: ratio of the perforated fin weight to that of the non-perforated fin.S: perforation spacing T: temperaturet: fin thicknessW: fin widthSubscripts and superscriptsb: fin basel: lower surface of finmax: maximumpc: perforation inner surface (within the perforation)pf: perforated finps: remaining solid portion of the perforated finsf: solid (non-perforated) finss: solid surfacet: fin tipu: upper surface of finx: longitudinal direction or coordinate y: transverse (lateral) direction with the fin width or coordinate z: transverse (lateral) direction with the fin thickness or coordinate  : ambient
: ambient
References
| [1] | A. E. Bergles, Technique to augment heat transfer. In Handbook of heat transfer Applications, (Edited by Werren M . Rohsenow, James P. Hartnett, and Ejup N. Ganic), Ch. 3, Second Edition, McGraw-Hill Book company, NY. |
| [2] | Abdullah H. AlEssa, Mohamad I. Al-Widyan, “Enhancement of natural convection heat transfer from a fin by triangular perforation of bases parallel and toward its tip", Applied Mathematics and Mechanics 2008, 29(8):1033–1044. |
| [3] | R. Mullisen and R. Loehrke, A study of flow mechanisms responsible for heat transfer enhancement in interrupted-plate heat exchangers, Journal of Heat Transfer (Transactions of the ASME) 108, 377-385 (1986). |
| [4] | B. V. S. S. S. Prasad, A. V. S. S. K. S. Gupta, “ Note on the performance of an optimal straight rectangular fin with a semicircular cut at the tip”, Heat transfer engineering Vol. 14 , No. 1 1998. |
| [5] | C. F. Kutscher, Heat exchange effectiveness and pressure drop for air flow through perforated plates with and without crosswind, Journal of Heat transfer 116, 391-399, (May 1994). |
| [6] | B. T. F. Chung and J.R.Iyer, “ Optimum design of longitudinal rectangular fins and cylindrical spines with variable heat transfer coefficient”, Heat transfer engineering Vol. 14 no. 1 1993 , P31-42. |
| [7] | S.Kakac, A. E. Bergles, F. Mayinger , “ Heat Exchangers, Thermal- Hydraulic Fundamentals and Design” , Hemisphere Publishing Corporation, 1981. |
| [8] | Al-Essa, A.H., 2000, “Enhancement of thermal performance of fins subjected to natural convection through body perforation”, Ph.D. thesis, Department of Mechanical Engineering, University of Baghdad, Iraq and University of Science and Technology. Jordan. |
| [9] | G. D. Raithby, K. G. T. Holands, Natural convection. In Handbook of Heat Transfer Applications (2nd Edn) (Edited by W. Rohsenow, J. Hartnett and E. Ganic), , Ch. 6. McGraw-Hill Book company, New York (1984). |
| [10] | E. M. Sparrow and M. Carranco Oritz , “ Heat transfer coefficient for the upstream face of a perforated plate positioned normal to an oncoming flow ” , Int. J. Heat Mass Transfer. Vol. 25,No. 1, PP 127 – 135 , 1982. |
| [11] | A. Aziz and V. Lunadini, Multidimensional steady conduction in convicting, radiating, and convicting-radiating fins and fin assemblies, Heat Transfer Engineering 16(3), 32-64 (1995). |
| [12] | P. Razelos and E. Georgiou , “Two–Dimensional effects and design criteria for convective extended surfaces”, heat transfer engineering Vol.13, No.3, 1992, p 38-48 |
| [13] | Rao, S. S., "The Finite Element Method in Engineering", Second Edition, Elmsford, NY: Pergamon, 1989. |
| [14] | Abdullah H. M. AlEssa, "One Dimensional Finite Element Solution of the Rectangular Fin with Rectangular Perforations", WSEAS TRANSACTIONS on HEAT AND MASS TRANSFER, Issue 10, Volume 1, October 2006, p 762-768. |
| [15] | Frank P. Incropera and David P. Dewitt, Fundamentals of Heat and Mass Transfer (Forth Edition), p. 110, John Wiley and sons, New York (1996). |


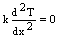
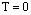
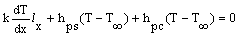
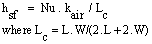
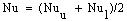
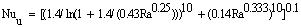
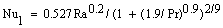

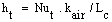
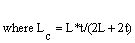 For the perforated fin there are three distinct heat transfer coefficients exist. The first one is the heat transfer coefficient of the solid portion of the perforated surfaces (hps) which can be calculated by the following expression[2]:
For the perforated fin there are three distinct heat transfer coefficients exist. The first one is the heat transfer coefficient of the solid portion of the perforated surfaces (hps) which can be calculated by the following expression[2]: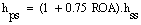
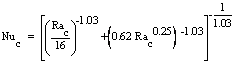 (11)The third one is that the heat transfer coefficient at fin tip (ht) which its Nusselt number (Nut) is given by equation (8). To measure the enhancement of the heat dissipation rate, it is an essential task to compare the performance of the perforated fin with that of the equivalent solid one. This can be performed by considering the ratio of heat dissipation of the perforated fin to that of the solid one (RQF) which can expressed as:
(11)The third one is that the heat transfer coefficient at fin tip (ht) which its Nusselt number (Nut) is given by equation (8). To measure the enhancement of the heat dissipation rate, it is an essential task to compare the performance of the perforated fin with that of the equivalent solid one. This can be performed by considering the ratio of heat dissipation of the perforated fin to that of the solid one (RQF) which can expressed as: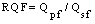
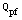 ) is computed according to the finite element heat transfer solution described in[14]. The heat dissipation of the solid fin (
) is computed according to the finite element heat transfer solution described in[14]. The heat dissipation of the solid fin (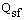 ) is computed according to the exact solution described in[15]. The material weight of the perforated fin is compared with that of the non-perforated one by weight ratio RWF which is given by:-
) is computed according to the exact solution described in[15]. The material weight of the perforated fin is compared with that of the non-perforated one by weight ratio RWF which is given by:-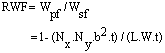






 : ambient
: ambient Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML