Mohammad M.Barzegari1, Morteza Dardel2, Alireza Fathi1, Mohammad H. Pashaei1
1Department of mechanical engineering, Babol, Iran
2Department of Mechanical Engineering, Babol University of Technology, Shariati Avenue, Babol, P.O. Box 484, Iran
Correspondence to: Morteza Dardel, Department of Mechanical Engineering, Babol University of Technology, Shariati Avenue, Babol, P.O. Box 484, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In last decades, smart materials have developed extensively, and have become an important topic for researchers in different areas. SMA is a good candidate for active control of the smart composite structures. In this study, numerical-based analysis for evaluating the natural frequencies and mode shapes of the plate with embedded shape memory alloy wires are presented. Plates are modelled in according to classical plate theory (CPT) as well as first-order shear deformation plate theory (FSDT). Also, SMA wires are modelled as a beam. The effect of axial load generated by SMA wires due the change of temperature on the natural frequencies is accurately studied.
Keywords:
shape memory alloy, natural frequency, shear deformation theory, buckling
Cite this paper: Mohammad M.Barzegari, Morteza Dardel, Alireza Fathi, Mohammad H. Pashaei, Effect of Shape Memory Alloy Wires on Natural Frequency of Plates, Journal of Mechanical Engineering and Automation, Vol. 2 No. 1, 2012, pp. 23-28. doi: 10.5923/j.jmea.20120201.05.
1. Introduction
So many structures like airplane’s wings could be modelled as a two-dimensional plate. With adding surface- bonded or embedded induced strain actuators to plate, it is possible to achieve active control in order to increase stability, reduce noise and vibrations. Strain actuators are generally made of smart materials. SMA is a good candidate for active control of the smart composite structures. In a low temperature, it is possible to make relatively large deformation such as bending, twisting, compressing or stretching. Also, it is possible to return to its original shape by heating. SMA actuators are generally embedded in structures with pre-strain. When an electric current pass throughout SMA wires, electric resistant of wires generate heat. Therefore, because of returning actuators to their original shape, a large internal force is generated, and this force is transmitted to structure. This generated force and also change in module of elasticity and density of SMA wires modify equal stiffness of structure, as well as increase failure limit of the system. Zhang et al. [1] have investigated the vibration characteristic of the laminated composite plates with unidirectional and woven SMAs by both impact vibration tests and theoretical analysis. Zak et al.[2] have studied the dynamic performance of a multi-layered composite plate with embedded shape memory alloy wires in terms of the changes in its relative fundamental natural frequency. Park et al.[3] have investigated the com posite plate embedded fibers that is subjected to aerodynamic and thermal loading in the supersonicregion. Ni et al. [4] have developed the epoxy resin composites filled with Ni-Ti alloy short fibers.There are different theories for vibration analysis of plates. Classical plate theory and first-order shear deformation plate theory are common theories that have been used to obtain frequencies and mode shapes. Classical plate theory is just suitable for thin plates, but first-order shear deformation plate theory could be used for moderate thick and thick plates.In the current study, natural frequencies and mode shapes of plate with different number of embedded SMA wires, for both below martensite finish temperature and above austenite finish temperature are numerically evaluated. These calculations are presented for different boundary conditions and different thicknesses of plate. The effect of axial load with critical buckling load and frequency jump are carefully studied.
2. Theoretical Model
In this paper, SMA wires are aligned along the x axis and they stand on a neutral axis (y is axis of symmetry). Figure 1 shows the schematic figure of the plate and SMA wires.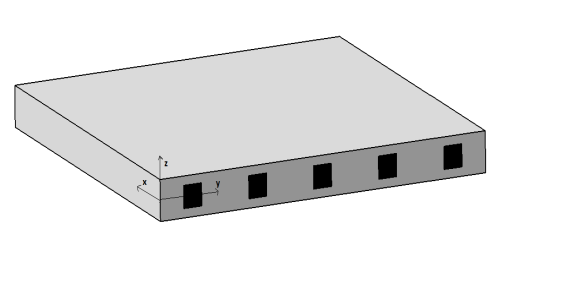 | Figure 1. Schematic illustration of the plate with embedded SMA wires |
Cross-sectional area of SMA wires is considered to be square. Since, the ratio of the SMA wire’s thickness to its length is too small, it can be modelled as a beam. Classical plate theory is based on assumptions similar to those used in Euler-Bernoulli beam theory. Also, FSDT is similar to Timoshenko beam theory. The equation of motion of the plate with SMA embedded wires can be obtained as follows.
2.1. Classical Plate Theory
According to CPT, displacement components of any points of a plate are given by[5]: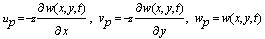 | (1) |
According to this theory, the kinetic energy of the plate (Tp) is given by[5]: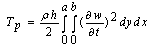 | (2) |
The strain energy of the system (Up) can be also expressed as[5]: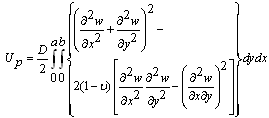 | (3) |
D is the flexural rigidity of the plate, and it can be determined as[5]: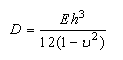 | (4) |
2.2. Euler-Bernoulli beam theory
In Euler-Bernoulli theory, displacement components of a point in the beam can be expressed as[6]: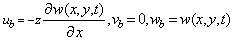 | (5) |
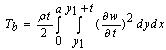 | (6) |
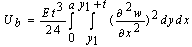 | (7) |
2.3. First-order Shear Deformation Plate Theory
For FSDT, displacement components of any point of plate are[6]: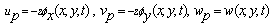 | (8) |
Strain energy of the plate can be expressed as[6]: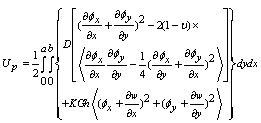 | (9) |
Kinetic energy can be determined as[6]: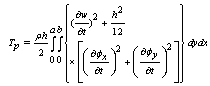 | (10) |
2.4. Timoshenko Beam Theory
According to Timoshenko beam theory, displacement components of any points of a beam are given by[6]: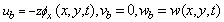 | (11) |
According to Timoshenko theory, Kinetic and strain energy of the beam can be expressed as[6]: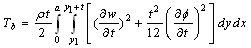 | (12) |
where K is considered to be 5/6. G can be expressed as: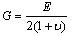 | (14) |
For better results, FSDT and Timoshenko theories can be modified as follow[6]: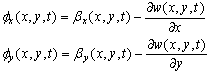 | (15) |
2.5. Modeling the effect of SMA wires
The recovery action of the pre-strained SMA wires generate axial stress that can be determined as[7]: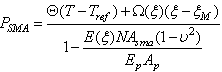 | (16) |
The transformation coefficient can be determined as[7]: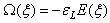 | (17) |
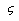 can be evaluated by [8]:
can be evaluated by [8]: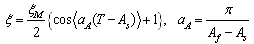 | (18) |
where 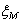 is considered to be 1.
is considered to be 1. 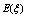 can be determined by using the mixture law:
can be determined by using the mixture law: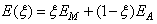 | (19) |
The work done by each SMA wire can be expressed as: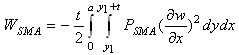 | (20) |
2.6. Obtaining the Natural Frequency
Total kinetic and strain energy (plate with embedded SMA wires) can be evaluated by: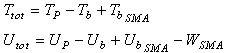 | (21) |
The module of elasticity and density of SMA are needed for calculating 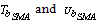 , where the mechanical properties of the plate should be considered for calculating of the terms of the Eq. (21).Final equation can be obtained from Lagrange’s equation as follows:
, where the mechanical properties of the plate should be considered for calculating of the terms of the Eq. (21).Final equation can be obtained from Lagrange’s equation as follows: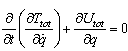 | (22) |
Using the separation of variables technique, w(x,y,t), βx(x,y,t) and βy(x,y,t) can be expressed as: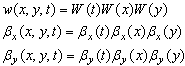 | (23) |
2.6.1. Classical plate and Euler-Bernoulli beam theory
For classic plate theory: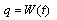 | (24) |
Substituting Eq. (24) into Eq. (22), gives: | (25) |
where [M]and [K] are mass and stiffness matrixes, respectively.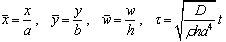 | (26) |
With considering Eq. (26), Eq. (25) can be rewritten as: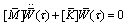 | (27) |
where 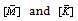 are dimensionless mass and stiffness matrixes of the system.
are dimensionless mass and stiffness matrixes of the system.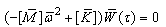 | (28) |
where 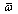 is dimensionless natural frequency and it can be obtained by solving the Eq. (29).
is dimensionless natural frequency and it can be obtained by solving the Eq. (29).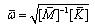 | (29) |
2.6.2. First-order Shear Deformation Plate and Timoshenko Beam Theory
For FSDT: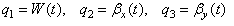 | (30) |
Substituting Eq. (30) into Eq. (22), gives: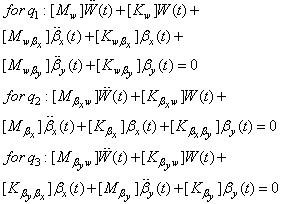 | (31) |
To make Eq. (31) dimensionless, following quantities could be used: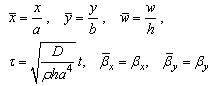 | (32) |
The dimensionless equation can be modified as: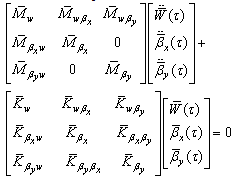 | (33) |
The solution of Eq. (33) is assumed to be harmonic. So, dimensionless natural frequency can be obtained as the same manner as used in Eq. (29), but in this state, 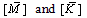 are introduced as follows:
are introduced as follows: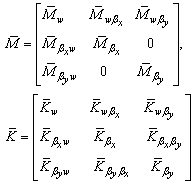 | (34) |
3. Results and Discussion
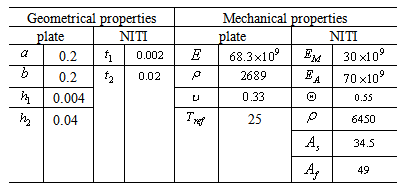
In the present study, square SMA wires, NITI have been considered. These wires have been pre-strained to 6.7% at a temperature below the martensite finish temperature Mf. The SMA wires are located at the middle layer of the plate and aligned along the x direction. Table 1 lists the mechanical and geometrical properties of SMA wires and aluminum alloy plate. Two applied temperature are used to calculate natural frequencies. One of them is under martensite temperature, equal to 5.6℃, and another one is above austenite temperature which is equal to 49℃.Natural frequencies are also evaluated for different number of SMA wires, and different boundary conditions. For evaluating the natural frequencies of the plate, its first and second mode shapes at x and y directions are considered. Plate is assumed as two perpendicular beams. The mode shapes of these beams for different boundary conditions are mentioned in[6]. Natural frequencies are calculated for two thickness of plate, h1 and h2. t1 and t2 are SMA wire’s thickness, too. This processes are performed for clamped- clamped-pinned-pinned (C-C-S-S) and clamped- free- free- free (C-F-F-F) plates.Figure 2 shows the natural frequencies of C-C-S-S plate with thickness of 4mm and different number of SMA wires at T=5.6℃, in according to CPT and FSDT theories. In this temperature, wires are in martensitic phase. In this figure, it is clear that as the number of the SMA wires increases, the first three natural frequencies of C-C-S-S plate with thickness of 1.4mm decrease slightly. In this condition, module of elasticity and density of total system are increased. Also the effect of density is greater than module of elasticity. According to the Eq. (16), the axial load at low temperature is small. Therefore, natural frequencies decrease with increase in number of wires. Since, the ratio of the plate’s thickness to its length is too small, the results of two theories are almost the same.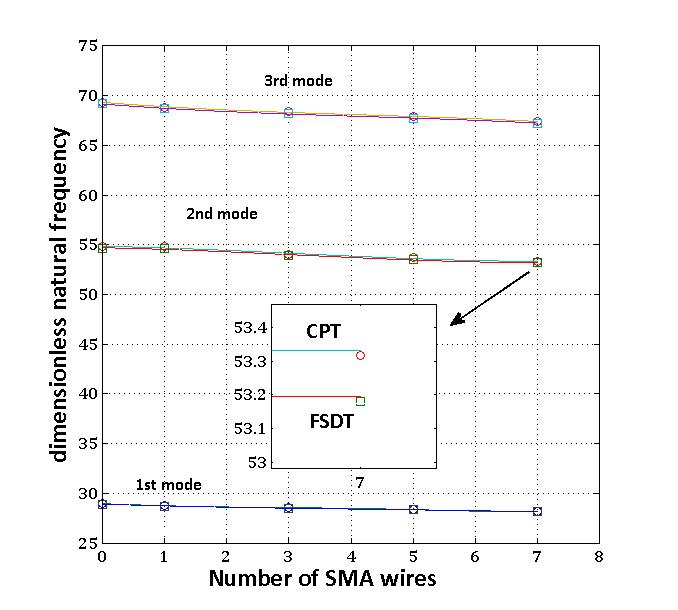 | Figure 2. Natural frequencies of CCSS plate with thickness of 4mm at T=5.6℃ |
Table 1. mechanical and geometrical properties of SMA wires and aluminum alloy plate
 |
| |
|
 | Figure 3. Natural frequencies of CCSS plate with thickness of 40mm at T=5.6℃ |
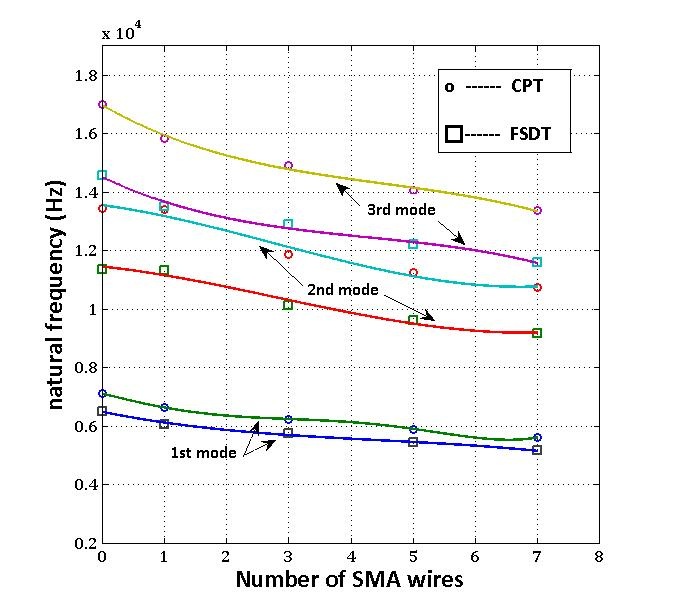
Figure 3 shows the natural frequencies of C-C-S-S plate with thickness of 40mm. As shown in Fig. 3, natural frequencies of C-C-S-S plate with thickness of 40mm have the same trends as that of previous condition, but the slope decrement is greater than that of the plate with thickness of 4mm. Also, due to ratio of the thickness to length, there are some differences between the results of two theories.Due to ignoring the shear deformation in CPT, the plate stiffness is assumed to be high which is expected. Hence their natural frequency prediction is greater than other theories. For other boundary conditions, changing in behaviour of the frequency is similar to that of C-C-S-S plate, but magnitudes of natural frequency differ from that of previous state.Figure 4 shows the natural frequencies of C-C-S-S plate with thickness of 4mm and different number of SMA wires at T=49℃. This temperature is above austenite temperature, in which module of elasticity of SMA wire increases. In this figure it can be seen, when the wires temperatures are above austenite finish temperature, the natural frequencies of C-C-S-S plate decrease with great slope as the number of SMA wires increases. Since axial load is compressive in this condition, and its magnitude is noticeable, buckling should be considered. When axial load becomes greater than critical buckling load, frequency jump will happen. For instance, as shown in Fig. 4, when the number of wires is seven, plate directly goes to its second mode shape, and if axial load becomes greater by increasing the number of wires, it goes to its upper mode.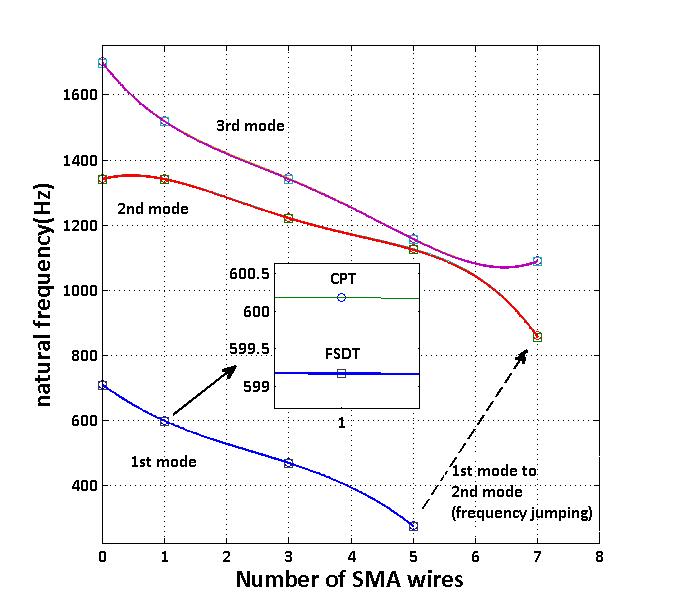 | Figure 4. Natural frequencies of CCSS plate with thickness of 4mm at T=49℃ |
Figure 5 shows the natural frequencies of C-F-F-F plate with thickness of 4mm and tensile axial load. So, an increase of number of SMA wires causes the increase of natural frequency. In this condition, slope has greater changes than previous case. Figure 6 shows the natural frequencies of C-F-F-F plate with thickness of 40mm. As shown in Fig. 6, there are some differences between the results of two theories.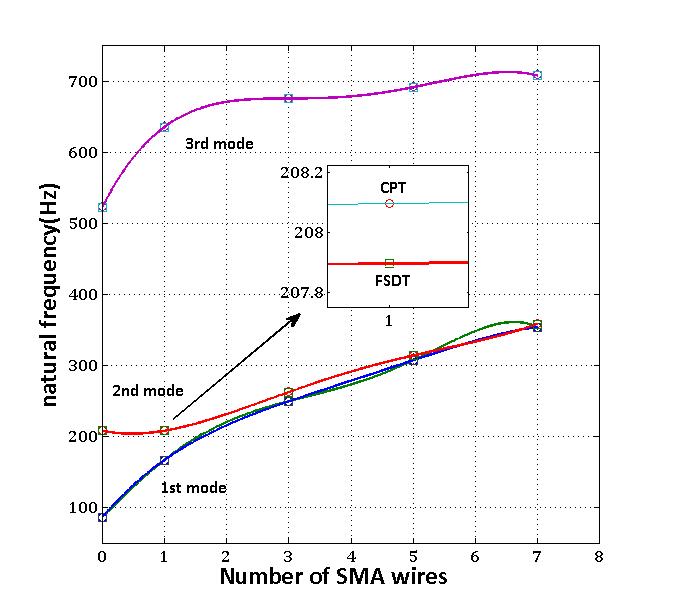 | Figure 5. Natural frequencies of CFFF plate with thickness of 4mm at T=49℃ |
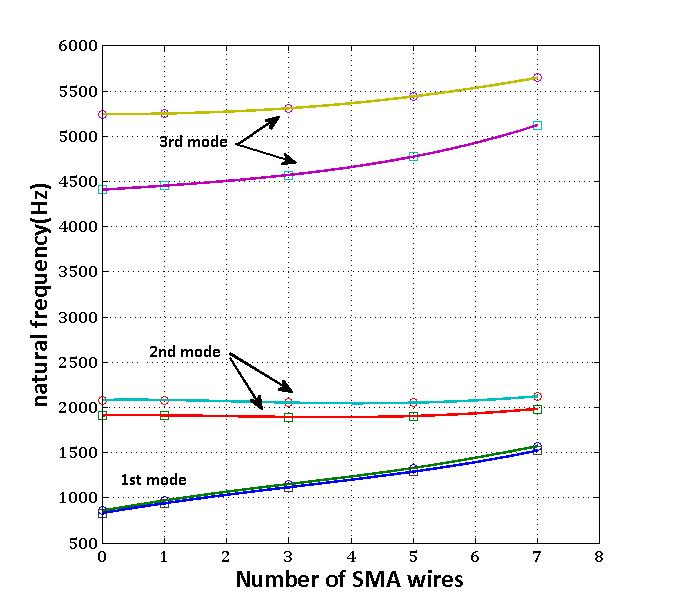 | Figure 6. Natural frequencies of CFFF plate with thickness of 40mm at T=49℃ |
Figure 7, 8 and 9 show the first, second and third mode shape of the plate.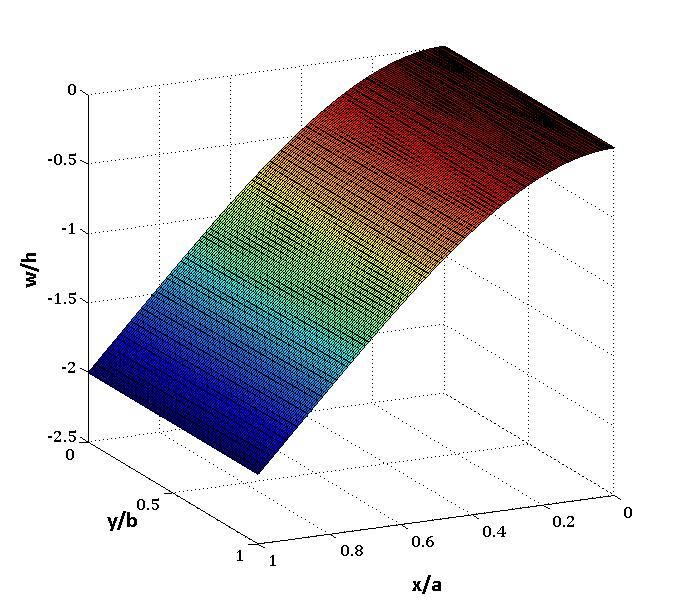 | Figure 7. The first mode shape of the plate |
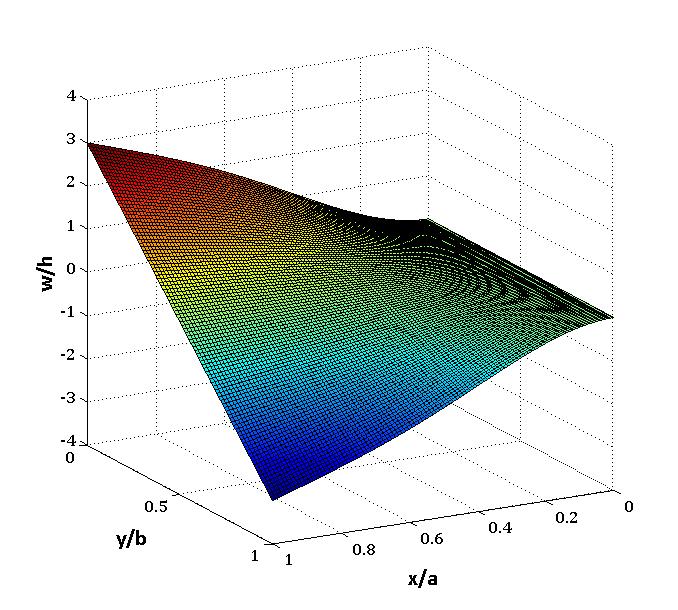 | Figure 8. The second mode shape of the plate |
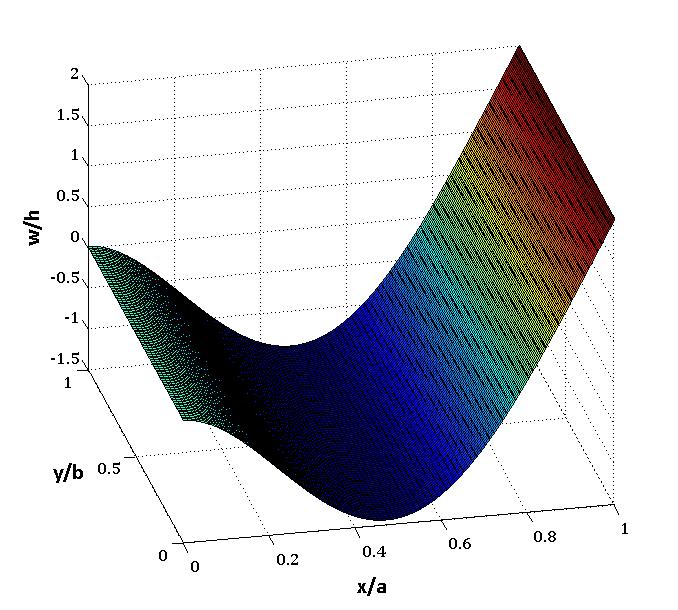 | Figure 9. The third mode shape of the plate |
4. Conclusions
In this study, a numerical study on natural frequency of plate with embedded SMA wire actuators are presented. This study is performed for plates with two different boundary conditions in according to classical plate theory and first- order shear deformation plate theory. In according to this study, with increasing the number of SMA wires, at a temperature under martensite finish temperature, the natural frequencies of plate decrease slightly. For clamped-clamped- pinned-pinned plates, natural frequencies at a temperature above austenite finish temperature decrease with a great slope and in this condition, when axial load’s magnitude is greater than critical buckling load, frequency jump occurs. With this jump, plate directly switches to its higher mode without transient from its lower modes due to the effect of axial force.
Nomenclature

References
| [1] | Zhang R.X., Ni Q.Q., Masuda A., Yamamura T. and Iwamoto M., 2006, “Vibration characteristics of laminated composite plates with embedded shape memory alloys”, Composite structures, 74:389-398. |
| [2] | Zak A.J., Cartmell M.P. and Ostachowicz W.M., 2003, “A sensitivity analysis of the dynamic performance of a composite plate with shape memory alloy wires”, composite structures, 60:145-157. |
| [3] | Park J.S., Kim J.H. and Moon S.H., 2005, “Thermal post-buckling and flutter characteristics of composite plates embedded with shape memory alloy fibers”, composites, 36:627-636. |
| [4] | Ni Q.Q., Zhang R.X., Natsuki T. and Iwamoto M., 2007, “Stiffness and vibration characteristics of SMA/ER3 composites with shape memory alloy short fibers”, composite structures, 79:501-507. |
| [5] | Wang C.M., Reddy J.N. and Lee K.H., 2000, “Shear Deformable beams and Plates”, Amsterdam, Elsevier. |
| [6] | Rao S.S., 2007, “Vibration of continuous systems, New Jersey”: Wiley. |
| [7] | Lau K.T., Zhou L.M. and Tao X.M., 2002, “Control of natural frequencies of a clamped–clamped composite beam with embedded shape memory alloy wires”, Composite structures, 58:39-47. |
| [8] | Liang C. and Rogers C.A., 1990, “One-dimensional thermo mechanical constitutive relations for shape memory materials”, Journal of Intelligent Material Systems and Structures, 8:285–302. |


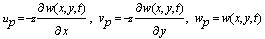
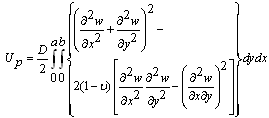
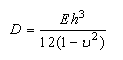
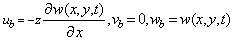
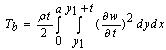
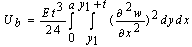
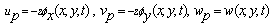
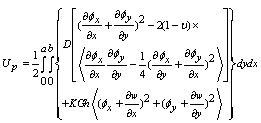
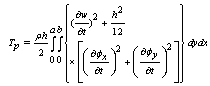
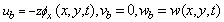
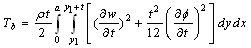
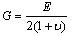
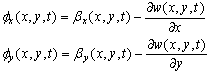
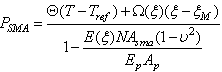
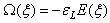
 can be evaluated by [8]:
can be evaluated by [8]: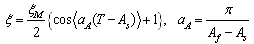
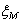 is considered to be 1.
is considered to be 1. 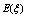 can be determined by using the mixture law:
can be determined by using the mixture law: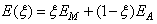
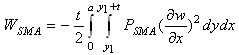
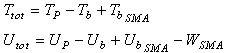
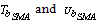 , where the mechanical properties of the plate should be considered for calculating of the terms of the Eq. (21).Final equation can be obtained from Lagrange’s equation as follows:
, where the mechanical properties of the plate should be considered for calculating of the terms of the Eq. (21).Final equation can be obtained from Lagrange’s equation as follows: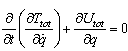
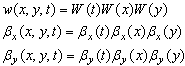
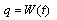

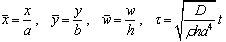
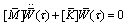
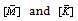 are dimensionless mass and stiffness matrixes of the system.
are dimensionless mass and stiffness matrixes of the system.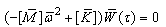
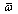 is dimensionless natural frequency and it can be obtained by solving the Eq. (29).
is dimensionless natural frequency and it can be obtained by solving the Eq. (29).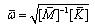
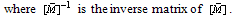
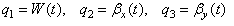
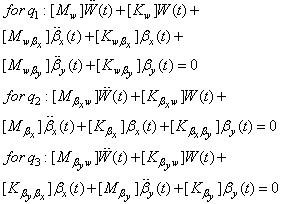
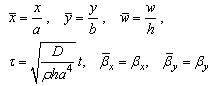
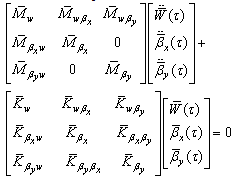
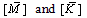 are introduced as follows:
are introduced as follows: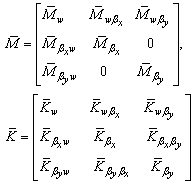









 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML