| [1] | Avdeef, A., 2012, pKa determination. In Absorption and Drug Development: Solubility, Permeability and Charge State. 2nd ed., Hoboken, NJ: Wiley, Chapter 3, pp. 129. |
| [2] | Avdeef, A., Testa, B., 2002, Physicochemical profiling in drug research; a brief survey of the state-of-the-art of experimental techniques. Cellular and Molecular Life Science, 59, 1681-1689. |
| [3] | Babic, S., Horvat, M. J. A., Pavlovic, M. D., Macan, K. M., 2007, Determination of pKa values of active pharmaceutical ingredients., Trends in Analytical Chemistry, 26 (11), 1043-1060. |
| [4] | Balogh, T. G., Tarcsay, A., Kescru, M. G., 2012, Comparative evaluation of pKa prediction tools on a drug discovery data set., Journal of Pharmaceutical and Biomedical Analysis, 67-68, 63-70. |
| [5] | Kerns, H. E., 2011, High throughput physicochemical profiling for drug discovery. Journal of Pharmaceutical Sciences, vol. 90 (11), 1838-1858. |
| [6] | Manallack, T. D., Prankecd, J. R., Yuriev, E., Opreale, I. T., Chalmersa, K. D., 2013, The significance of acid/base properties in drug discovery., Chemical Society Reviews, 42 (2), 485-496. |
| [7] | Nakashima, S., Yamamoto, K., Arai, Y. Ideda, Y., 2013, Impact of physicochemical profiling for rational approach on drug discovery., Chemical and Pharmaceutical Bulletin, 61 (12), 1229-1230. |
| [8] | Prankera, J. R., 2007, Critical Compilation of pKa values for Pharmaceutical Substances., Amsterdam: Elsevier. |
| [9] | Tietgen, H., Walden, M., 2013, Physicochemical Properties. In Drug Discovery and Evaluation: Safety and Pharmacokinetic Assays. 2nd ed., New York: Springer, pp. 1125-1138. |
| [10] | Asuero, A. G., 1989, A bilogarithmic method for the evaluation of acidity constants of amphoteric substances from solubility measurements. International Journal of Pharmaceutics, 52, 129-137. |
| [11] | Asuero, A. G., 1992, A hyperbolic cosine method for the spectrophotometric evaluation of acidity constants of two-step overlapping equilibria. International Journal of Pharmaceutics, 88, 15-22. |
| [12] | Pathare, B., Tambe, V., Patil, V. A., 2014, review on various analytical methods used in determination of dissociation constant., International Journal of Pharmacy and Pharmaceutical Sciences, 6 (8), 26-34. |
| [13] | Reijenga, J., Hoof, V. A., Loon, V. A., Teunisien, B., 2013, Development of methods for the determination of pKa values. Analytical Chemistry Insights, 8, 53-71. |
| [14] | Sistovaris, N., Hamachi, Y., Kuriki, T., 1991, Multifunctional substances- Determination of pKa-values by various methods. Fresenius Journal of Analytical Chemistry, 340, 345-349. |
| [15] | Zhou, L., Wang, J., 2008, Physico-chemical characterization in drug discovery. Trends in the Pharmaceutical Industry, 4, 12-18. |
| [16] | Zevatskii, Y. E., Samoilov, D. V., Mchedlov-Petrosyan, N. O., 2009, Contemporary methods for the experimental determination of dissociation constants of organic acids in solutions., Russian Journal of General Chemistry, 79 (9), 1859-1889. |
| [17] | Papanastasiou, G., Kokkinidis, G., 2003, Development of iterative methods for the exact determination of acid dissociation constants and specific reaction rates in various ionic or electrochemical systems. A review. Collection of Czechoslovak Chemical Communications, 68 (8), 1345-1378. |
| [18] | Asuero, A. G., Michalowski, T., 2011, Comprehensive formulation of titration curves for complex acid-base systems and its analytical implications. Critical Reviews in Analytical Chemistry, 41 (2), 151-187. |
| [19] | Alongi, K. S., Shields, G. C., 2010, Annual Reports in Computational Chemistry, Chapter 8 – Theoretical calculations of acid-dissociation constants: a review article, pp. 133-138. |
| [20] | Martell, A. E., 1992, Determination and Uses of Stability Constants. New York: Wiley. |
| [21] | Martell, A. E., Hancock, R. D., 1996, Metal Complexes in Aqueous Solution. New York: Springer. |
| [22] | Asuero, A. G., Herrador, M. A., Camean, A. M., 1986, Spectrophotometric evaluation of acidity constants of diprotic acids: errors envolved as a consequence o an erroneous choice of the limit absorbance. Analytical Letters, 19 (19-20), 1867-1880. |
| [23] | Asuero, A. G., Jimenez-Trillo, J. L., Navas, M. J., 1986, Spectrophotometric methods for the evaluation of acidity constants—I. Numerical methods for single equilibria. Talanta, 33 (6), 531-535. |
| [24] | Asuero, A. G., Jimenez-Trillo, J. L., Navas, M. J., 1986, Mathematical treatment of absorbance versus pH graphs of polybasic acids. Talanta, 33 (11), 929-934. |
| [25] | Palalikit, D., Block, J. H., 1980, Determination of ionization constants by chromatography. Analytical Chemistry, 52 (4), 624-30. |
| [26] | Budesinsky, B. W., 1969, Acidity of several chromotropic acid azo derivatives. Talanta, 16 (9), 1277-1288. |
| [27] | Asuero, A. G., Recamales, M. A., 1993, A bilogarithmic method for the spectrophotometric evaluation evaluation of acidity constants of two-step overlapping equilibria. Analytical Letters, 26 (1), 163-181. |
| [28] | Asuero, A. G., 2009, A Hiperbolic Sine Procedure for the Spectrophotometric Evaluation of Acidity Constants for Two-Step Overlapping Equilibria. Journal of Analytical Chemistry, 64 (10), 1026-1030. |
| [29] | Asuero, A. G., Navas, M. J., Jimenez-Trillo, J. L., Spectrophotometric methods for the evaluation of acidity constants-II: Numerical methods for two-step overlapping equilibria., Talanta, 33 (6), 195. |
| [30] | Meites, L., 1981, An Introduction to Chemical Equilibrium and Kinetics. Oxford: Pergamon Press. |
| [31] | Asuero, A. G., Herrador, M. A., Jimenez, A. M., 1986, A Three Equation Method for the Numerical Evaluation of Acidity Constants of Single Equilibria from Spectrophotometric Data., Analytical Letters, 19 (7-8), 837-843. |
| [32] | Matsumoto, P. S., Ring, J., Zhu, J. L., 2008, The use of limits in an advance placement chemistry course. Journal of Chemical Education, 84 (10), 1655-1658. |
| [33] | Missen, R. W., 1977, Applications of the L’Hôpital-Bernoulli rule in chemical systems. Journal of Chemical Education, 54 (8), 488-490. |
| [34] | Herrador, M. A., Jimenez, A. M., Asuero, A. G., 1987, Spectrophotometric evaluation of acidity constants of methylglyoxal bis(4-phenyl-3-thiosemicarbazone)., Acta Pharmaceutica Technologica, 33(2), 74-90. |
| [35] | Polster, J., 2006, Chromatography, Titration, and Reaction Kinetics: UV-VIS Spectroscopic Evaluation on the Basis of the Mauser Diagrams, Research Signpost. Kerala, India: Trivandrum. |
| [36] | Polster, J., 1995, Reaktionskinetische Auswertung spektroskopischer Medβdaten. Eine Einführung in die kinetische Analyse chemischer und photochemischer Reaktionen. Wiesbaden: Vieweg. |
| [37] | Polster, J., Lachmann, H., 1989, Spectrometric Titrations. Analysis of Chemical Equilibria. Weinheim: VCH. |
| [38] | Polster, J., 1982, Spektrometrische Titration. Teil II. GIT Labor-Fachzeitschrift 26 (6), 581-592. |
| [39] | Polster, J., 1975, Über eine allgemeine graphische Methode zur Analyse von mehrstufigen spektrophotometrischen Titrationsgleichgewichten. Analysis of multistep spectrophotometric titration equilibria by means of a general graphical method. Zeitschrift für Physikalische Chemie Neue Folge, 97, S55-68. |
| [40] | Coleman, J. S., Varga, L. P., Mastin, H. S., 1970, Graphical methods for determining the number of species in solution from spectrophotometric data. Inorganic Chemistry, 9, 1015. |
| [41] | Rossotti, H., 1978, The Study of Ionic Equilibria. An Introduction. London: Longman. |
| [42] | Linnet, K., 1998, Performance of Deming regression techniques analysis in case of misspecified analytical error ratio in method comparison studies., Clinical Chemistry, 44 (5), 1024-1031. |
| [43] | Linnet, K., 1993, Evaluation of regression procedures for method comparison studies. Clinical Chemistry, 39 (3), 424-432. |
| [44] | Ripley, B. D., Thompson, M., 1987, Regression techniques for the detection of analytical bias. Analyst, 112, 377-383. |
| [45] | Thompson, M., 1982, Regression methods in the comparison of accuracy. Analyst, 107, 1169-1180. |
| [46] | Boccio, M., Sayago, A., Asuero, A. G., 2006, A bilogarithmic method for the spectrophotometric evaluation of stability constants of 1:1 weak complexes from the mole ratio data., International Journal of Pharmaceutics, vol. 318, 70-77. |
| [47] | McCartin, B. J., 2010, Oblique linear least squares approximation. Applied Mathematical Sciences, 58 (4), 2891-2904. |
| [48] | McCartin, B. J., 2003, A geometric characterization of linear regression. Statistics, 37 (2), 101-117. |
| [49] | Asuero, A. G., Gonzalez, G., de Pablos, F., Ariza, J. L., 1988, Determination of the optimum working range in spectrophotometric procedures., Talanta, 35 (7), 531-537, |
| [50] | Martín, J., Padilla Mairena, J., Asuero, A. G., 2016, On the Evaluation of Autoprotolysis Constans of Amphiprotic and Inert Solvents from Electrochemical Measurements: Consideration of Liquid Junction Potentials when Necessary. Current Topics in Analytical Chemistry, 10, 43-71. |
| [51] | Bayne, C. K., Rubin, I. B., 1986, Practical Experimental Designs and Optimization Methods for Chemists. Deerfield Beach, FL: VCH. |
| [52] | Kowalski, B. R., 1980, Chemometrics., Analytical Chemistry, 52 (5), 112R-122R. |
| [53] | Tripathi, A. K. Khan, K. R. Taneja, S. C., 2003, Reaction of Resorcinol with Mesityl Oxide: Synthesis of 2,2-Dimethyl-4-formyl- 7-methoxy-(2 H)-1-benzopyran., Synthetic Communications 33,
579–585. |
| [54] | Bouchoux, G. Defaye, D. McMahon, T. Likholyot, A. Mo, O. Yañez, M., 2002,
Structural and Energetic Aspects of the Protonation of Phenol, Catechol, Resorcinol, and Hydroquinone. Chemistry. A European Journal, 8, 2900–2909. |
| [55] | Cartensen, J. T. Rhodes, C.T. Drug Stability, 3rd ed., Marcel Dekker,
1999, pp. 145–189, 209–260. |
| [56] | Wells, J. I. Pharmaceutical Preformulation: The Physicochemical
Properties of Drug Substances, Ellis Harwood, England, 1990, pp. 15,
80. |
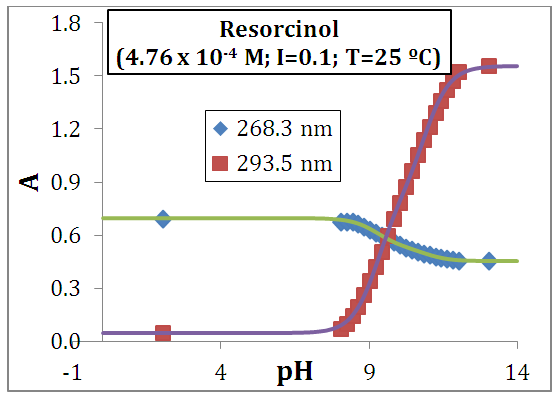
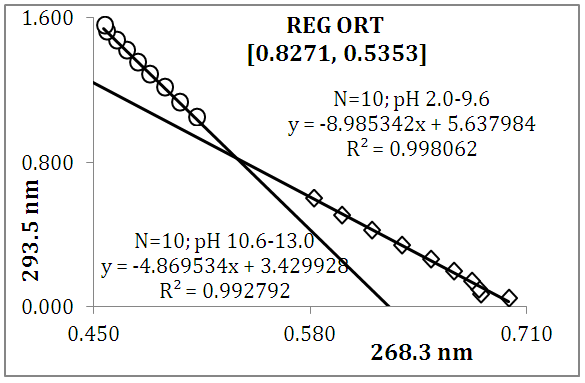
| [57] | Blanco, S. E., Almandoz, M. C., Ferretti, F. H., 2005, Determination of the overlapping pKa values of resorcinol using UV-visible spectroscopy and DFT methods. Spectrochimica Acta A, 61, 93-102. |

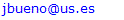

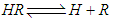
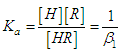
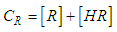
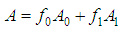
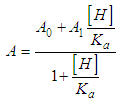
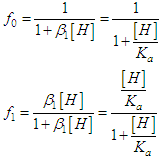
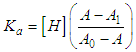
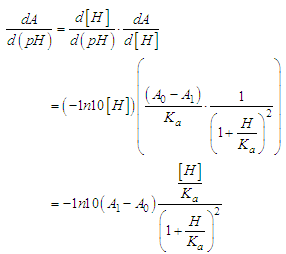
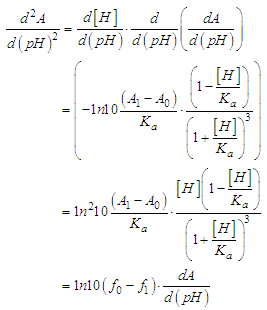
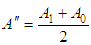
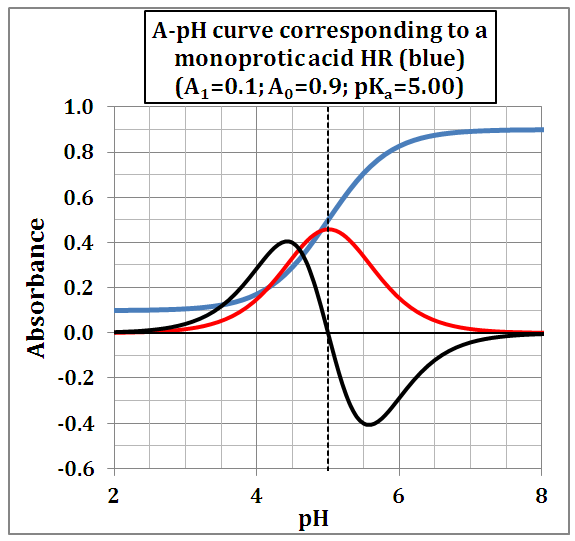
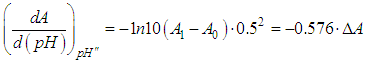
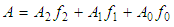
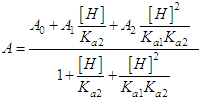
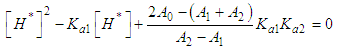
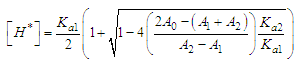
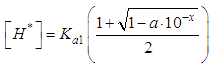
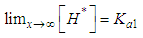
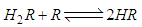
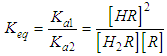
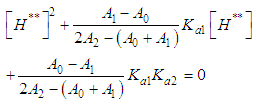
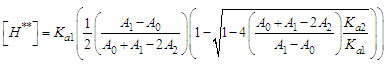
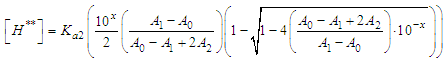
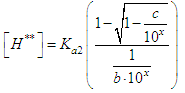
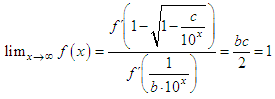
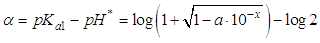
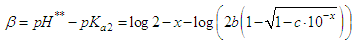
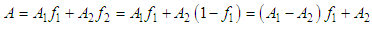
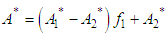
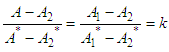
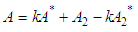
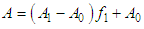
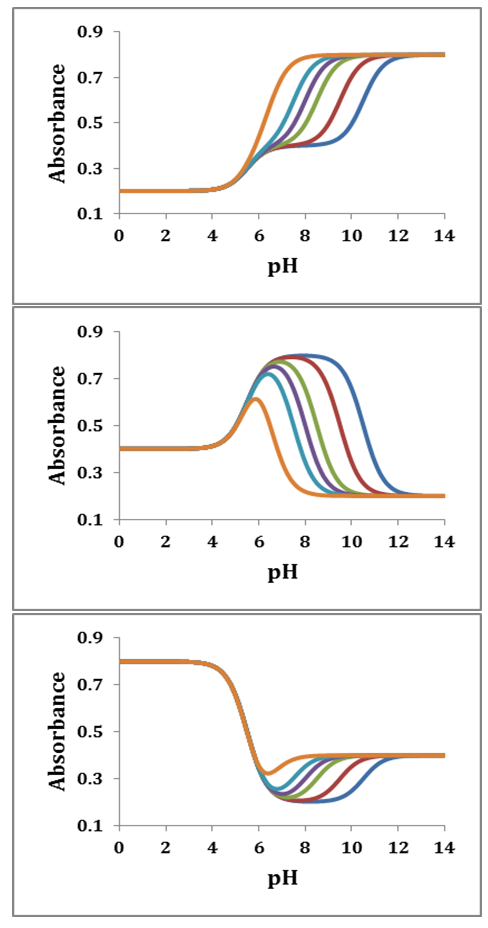
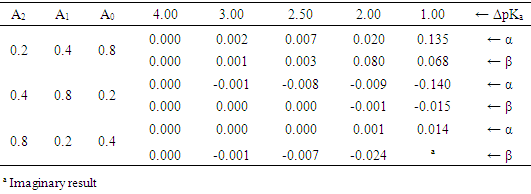
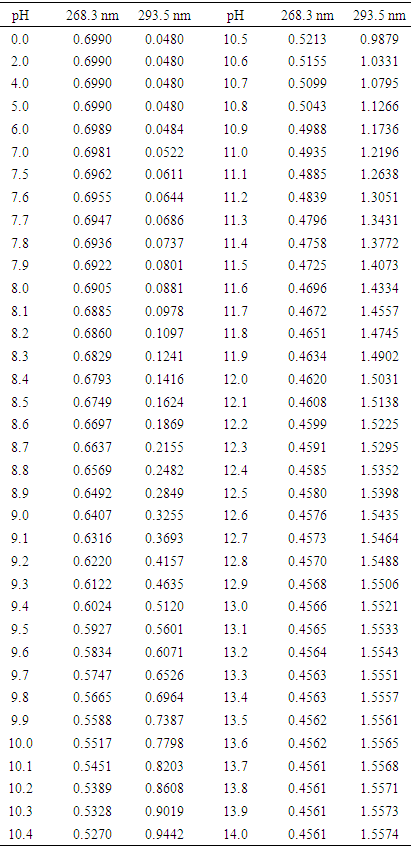
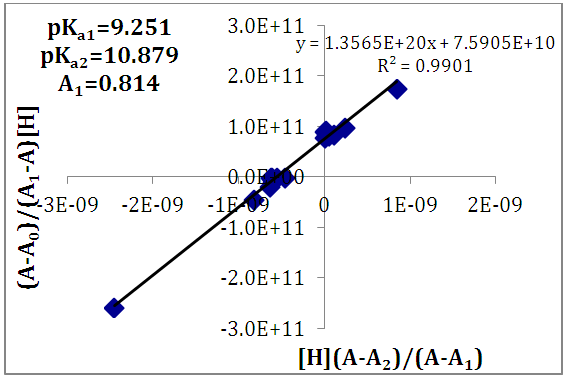
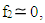 and then from measurements at two wavelengths λ and λ* we have
and then from measurements at two wavelengths λ and λ* we have
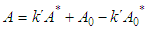
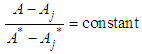
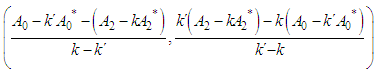
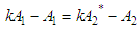
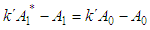
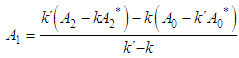
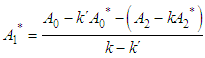
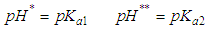
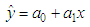
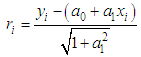
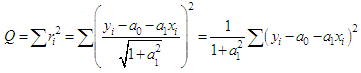
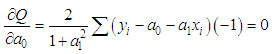
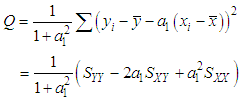
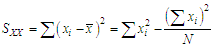
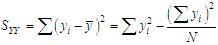
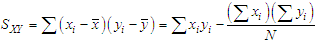
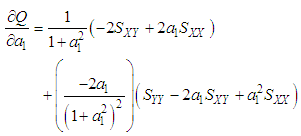
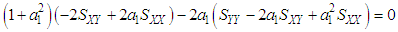
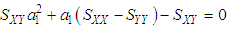
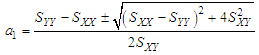
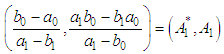
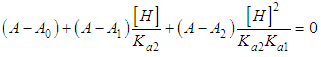
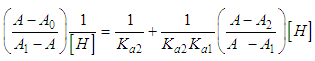
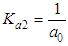
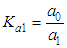
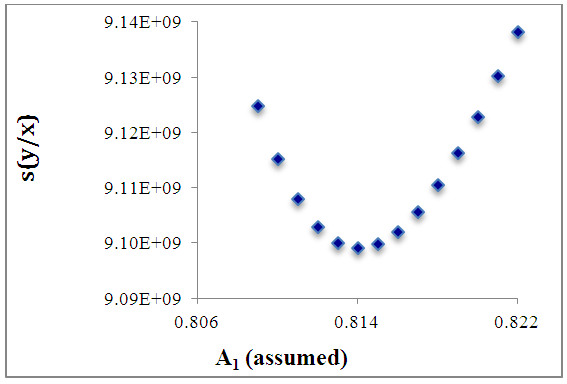
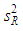 of a continuous arbitrary function of multiple variables, x1, x2 ... xN, which are normally distributed with variances
of a continuous arbitrary function of multiple variables, x1, x2 ... xN, which are normally distributed with variances 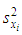 , is known as the law of random error propagation [49, 50], which is expressed as
, is known as the law of random error propagation [49, 50], which is expressed as 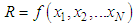
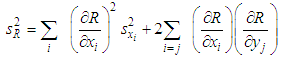
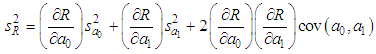
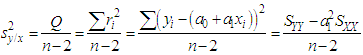
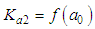
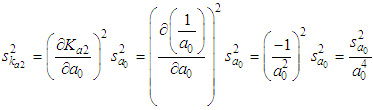
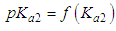
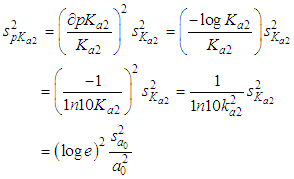
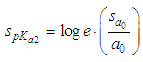
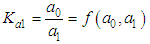
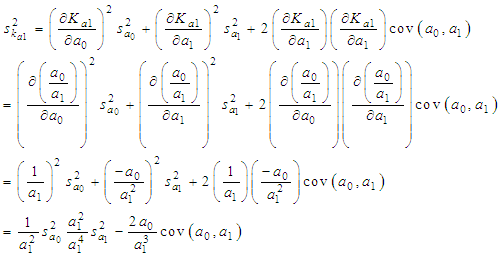
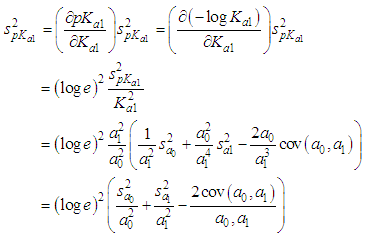
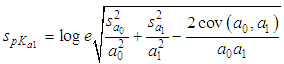
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML