Djameleddine Khatmi1, 2, Yannick Carissan1, Denis Hagebaum-Reignier1, Nicolas Goudard1, Stéphane Humbel1
1Aix Marseille Univ, CNRS, Centrale Marseille, iSm2, Marseille, France
2Laboratoire de Chimie Computationelle et Nanostructures, Université 8 mai 45- Guelma, Algérie
Correspondence to: Stéphane Humbel, Aix Marseille Univ, CNRS, Centrale Marseille, iSm2, Marseille, France.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The introduction of computational chemistry experiments for undergraduate students in sciences can really facilitate knowledge acquisition. It can make consistent various concepts in chemistry without a lengthy experimental protocol involving synthesis and physical chemistry mesurements. In the present case the students use a very simple molecular modeling program that we implemented: HuLiS. The computational chemistry experiment described herein is devoted to an important concept in chemistry: resonance between Lewis structures (mesomerism). In this context, conjugated ring species, as herein, are somewhat specific in the sense that aromaticity can play an important role. Hence, we discuss here a rather advanced resonance effect, where the usual qualitative rules do not suffice by themselves, but aromaticity and the “4n+2 electron” rule must be considered. This Hückel rule can be numerically displayed with an appropriate computational experiment. We use our free java applet (HuLiS) designed to evaluate the weights of resonance structures. As it is based on Hückel theory, the computations are fast, and the theoretical background is much simpler than with ab initio programs, hence the teachers are likely to master the tool used by the students. Upon substitutions, the weights of the zwitterionic Lewis structures adapt to the electronegativity. This is an opportunity to discuss the role of electronegativity in mesomerism, and strengthen the knowledge of the students.
Keywords:
Resonance, Aromaticity, Hückel, Lewis structures
Cite this paper: Djameleddine Khatmi, Yannick Carissan, Denis Hagebaum-Reignier, Nicolas Goudard, Stéphane Humbel, Mesomerism, Ring & Substituent Effects, A Computational Chemistry Experiments, Journal of Laboratory Chemical Education, Vol. 4 No. 2, 2016, pp. 25-34. doi: 10.5923/j.jlce.20160402.01.
1. Introduction
Three rules can be put forth when mesomerism is taught: the octet rule, the lead of neutral forms over zwitterionics and the consistency of charges with electronegativity. Major and minor Lewis structures are in principle defined with these simple rules. However, there are cases where conjugated rings can have an aromatic character as defined by the Hückel rule: when there are 4n+2 electrons in the ring. These structures can be expected to have a large weight, while those with 4n electrons are antiaromatic and can be expected to have small weights. The laboratory (numerical) experiment described here exemplifies nicely this point with methylenecyclopropene. Subsequent substitutions are used to show the role of electronegativity as well. It is designed to be part of the second-third year chemistry laboratory, when students are familiar with both resonance and aromaticity. [1] More details about aromaticity can be found in several other publications. [2-5] The three membered ring methylenecyclopropene, lead to two categories of Lewis structures, those with a cyclopropenyl cation which are considered as aromatic because they have two electrons in the ring (Scheme 1), and those with a cyclopropenyl anion with 4 electrons in the ring, [6] anti-aromatic. [4, 7-10] In the computational experiments described here these concepts of aromaticity/antiaromaticity dominate.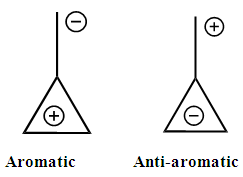 | Scheme 1. |
2. HuLiS Presentation
The computational experiments described herein are conceptually simple. They are performed with our HuLiS [11, 12] applet, which works like any standard Hückel program (SHMO for instance). [13] HuLiS is indeed also an Hückel program, but in addition it can compute the weights of resonance structures. To the best of our knowledge there are no other program equivalent to HuLiS. It is easy to use, requires a very basic knowledge of computational chemistry and only a few minutes are sufficient for its mastery. HuLiS is available for all systems including mobiles (smartphones, tablets, etc …). It can run as a Java applet or in a web browser. It can be found at http://www.hulis.free.fr. The Java version is preferred, particularly if the network cannot be accessed from the classroom computers: it can be downloaded as a single file onto the teacher’s computer, and then installed on all classroom computers (Windows, Linux and Mac OS). For mobiles, we made an html5 version that can be used in a web browser from http://m.hulis.free.fr. This version also runs on classroom computers, but the network is necessary in that case. The two HuLiS versions (Java and mobile) are basically the same, only small differences in the interface can be noticed. In the following we used the HuLiS-Java interface (Figure 1a).The central panel is used to draw the molecule, and the side panels, labeled either Hückel or Lewis, are used to control the program. The left (blue) panel is for Hückel. Its main function is to manage the display of the Hückel results obtained for the delocalized structure displayed in the central panel. The buttons are self-explicit, but the interested reader can refer to the manual. The right panel (orange) is used to manage Lewis structures. They are copies of the delocalized structure, but the orbitals have localization constraints [14] to describe lone pairs and bonds. The student can build directly a carbon skeleton of the molecule in the central panel (white), and automatically generate the Lewis structures by pressing the “Generate All” button at the top of the Lewis tools panel. The program searches for the best combination of Lewis structures that mimics the delocalized wave function.Note that, in addition to the usual Lewis structures, HuLiS can automatically generate bi-radical structures. In the present experiment, their weights are small. Moreover, the trust factor is not dramatically changed when they are removed. We recommend discarding the bi-radical structures generation at the beginning of the experiment. To do so, use the preferences panel (Figure 1b).# 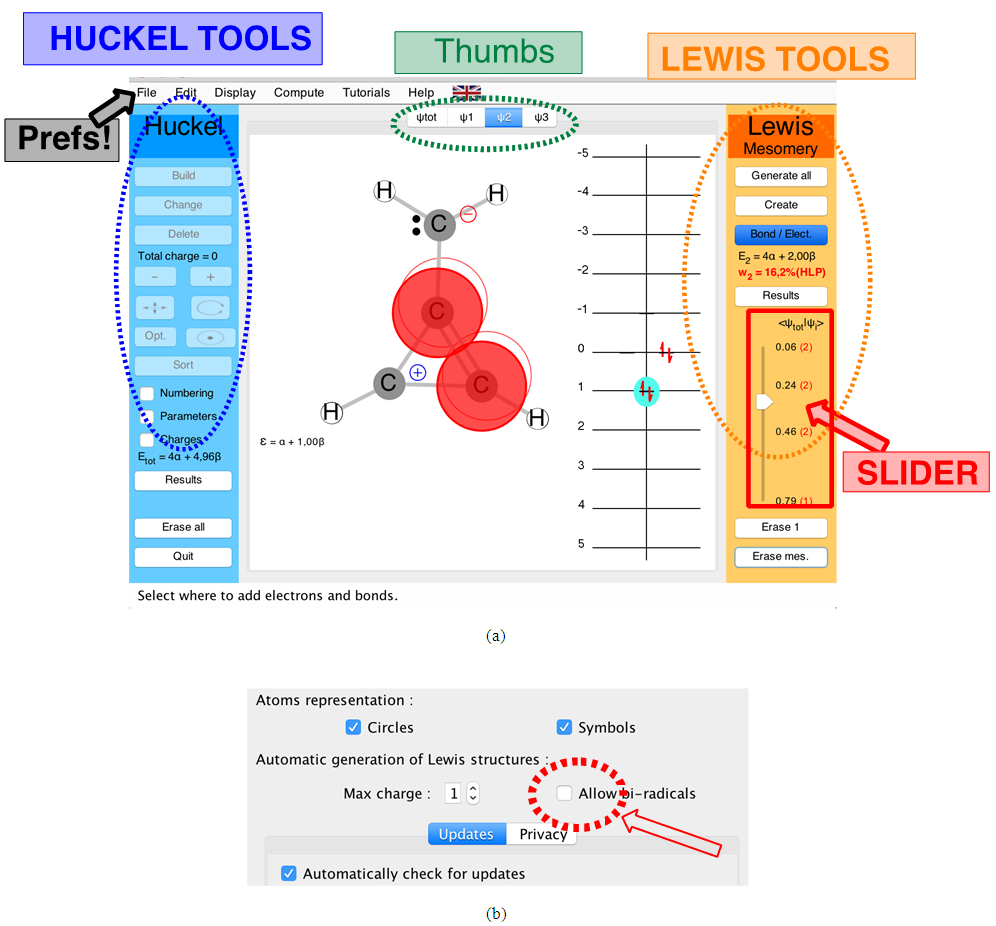 | Figure 1. (a) The main and the side panels or buttons in HuLiS interface. (b) part of the preference panel (Java version) |
A trust factor 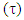 associated to the Lewis structures combination is computed as well. It is defined as the overlap between the Hückel wave function, which is the reference wave function, and the combination of Lewis Structures. When
associated to the Lewis structures combination is computed as well. It is defined as the overlap between the Hückel wave function, which is the reference wave function, and the combination of Lewis Structures. When 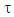 is larger than 90%, we consider that the combination of the Lewis structures adequately mimics Hückel’s. A low trust factor
is larger than 90%, we consider that the combination of the Lewis structures adequately mimics Hückel’s. A low trust factor 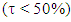 should be considered as a warning that the structures are not adequately selected. The user must then add new (and appropriate) structures. New Lewis structures can be add/rmodified with the mouse. The overlap of a structure with the Hückel wavefunction defines the relevance of the Lewis structure. A slider is used to select most relevant structures. Orbitals and Hückel energies are computed on the fly, and energy levels appear on a ladder, to the right of the central panel. When an energy level is selected, the corresponding orbital is plotted. If the central panel displays a Lewis structure, all the orbitals obey the localization constraint, as displayed in Figure 1a. If the central panel displays the delocalized structure, the orbitals are delocalized, as in regular Hückel computations. In the Java version the Lewis structures are in thumbs at the top, with just the label of the structure written on. By a click on a thumb, the user displays the corresponding Lewis structure (Figure 1a). A vertical slider is displayed in the Lewis panel. It can be used to select the most relevant set of Lewis structures among a basis of Lewis structures. The coefficient and the weight of each structure are displayed together with its energy above the slider. These numbers can be obtained through the results button of the Lewis panel. How HuLiS works has been described elsewhere. [12, 14, 15, 16] In the version for mobiles there is a graphical summary at the bottom, with stamps of each structure. The boxes are blue for the delocalized structure and orange for the Lewis’. These stamps replace the thumb, and are used to switch between structures. We put the slider above the stamps with a red round shape cursor.
should be considered as a warning that the structures are not adequately selected. The user must then add new (and appropriate) structures. New Lewis structures can be add/rmodified with the mouse. The overlap of a structure with the Hückel wavefunction defines the relevance of the Lewis structure. A slider is used to select most relevant structures. Orbitals and Hückel energies are computed on the fly, and energy levels appear on a ladder, to the right of the central panel. When an energy level is selected, the corresponding orbital is plotted. If the central panel displays a Lewis structure, all the orbitals obey the localization constraint, as displayed in Figure 1a. If the central panel displays the delocalized structure, the orbitals are delocalized, as in regular Hückel computations. In the Java version the Lewis structures are in thumbs at the top, with just the label of the structure written on. By a click on a thumb, the user displays the corresponding Lewis structure (Figure 1a). A vertical slider is displayed in the Lewis panel. It can be used to select the most relevant set of Lewis structures among a basis of Lewis structures. The coefficient and the weight of each structure are displayed together with its energy above the slider. These numbers can be obtained through the results button of the Lewis panel. How HuLiS works has been described elsewhere. [12, 14, 15, 16] In the version for mobiles there is a graphical summary at the bottom, with stamps of each structure. The boxes are blue for the delocalized structure and orange for the Lewis’. These stamps replace the thumb, and are used to switch between structures. We put the slider above the stamps with a red round shape cursor.
3. Experiment Overview
This computational chemistry experiment is divided into four sections (Figure 2). Undergraduate students can complete it in a 2-3 hour period. Considering that all students know Lewis structures and mesomerism, for the three first parts, the prerequisite are (i) a basic knowledge in electronegativity and (ii) the Huckel’s rules about aromaticity. However the fourth part, which was added, can require some knowledge in quantum chemistry. 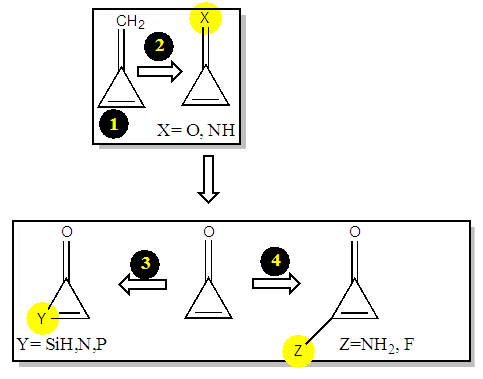 | Figure 2. The general scheme of the computational experiment |
All students can work individually with the instructor providing help and answering questions as needed. They firstly perform a prelab exercise with the drawings of the a priori important resonance structures. Then, they turn to the computational experiment to determine the actual weights of the structures. This shows how important are the structures with an aromatic character. They can also see that anti-aromatic structures can be discarded because they have a weigth close to zero.The three next sections are dedicated to study the effects of substitutions on the weights. In the second part, the students are requested to replace the exocyclic carbon by a more electronegative atom (N and O). In part 3, it is a carbon of the cycle that is replaced. Last, part 4, other substitutions will also be considered (Figure 2).
3.1. Prelab Exercise
Before starting this computational experiment students need to have a general overview on what they are looking for. That’s why a prelab exercise is described, and it must be done without the computer in order to formulate a prediction on the results, which is essential before undertaking the calculations. On a separate sheet of paper, students draw the different resonance forms of methylenecyclopropene. The full resonance scheme is shown on Figure 3. Structure IIa and IIb come from the red arrows, they have a negatively charged exocyclic carbon and a cycle with 2 electrons. The exocyclic carbon in structures IIIa and IIIb is positively charged. They come from the blue arrows (in I) and the cycle has 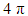 electrons.
electrons.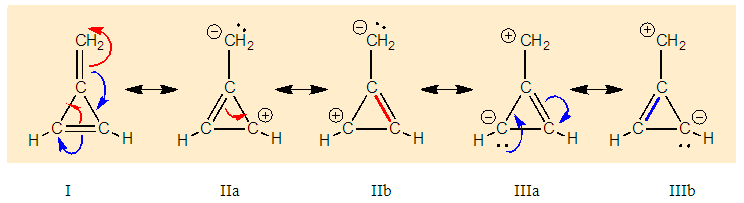 | Figure 3. Resonance structures of methylenecyclopropene. Because a bond implicitly contains some ionic components, the zwitterionic structures IIc and IIIc (see the note) are already included in I |
Note about other zwitterionic structures: in addition to the five structures shown in Figure 3, students can draw two additional zwitterionic structures (IIc and IIIc below), where the charge separation is located on two neighboring atoms. The tutor can let them do so; the forthcoming computation will actually show them that these structures can be discarded because they do not modify significantly the trust factor (see Table 1). The reason is simply that the two last structures are already included in the first one (I): whenever a bond is defined between two identical atoms, the electron sharing includes some ionicity, half of IIc, half of IIIc.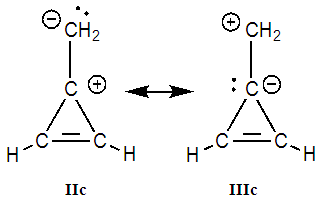 The students are then asked to order the structures from the most important to the least important. If only the octet and charge separation rules are considered, structure I is the major structure, and the four others are equivalent because they all have a single charge separation. They are considered as minor structures because they violate the octet rule, and they all have the same weight because the charge separation is alike. At this stage the reasonning is qualitative. Neglecting any other consideration, we have wIIa = wIIb = wIIIa = wIIIb = w’ < wI. Moreover, the charge of the exo-cyclic carbon could be crudely estimated to be null because it corresponds roughly to the weighted average of its charge in each structure qC1=wI*0+ w’*(-1-1+1+1)=0. Hence the exo-cyclic carbon would be electrically neutral if only the octet rule and the charge separation rule are considered. However, the exo-cyclic carbon is experimentally known to be negatively charged, [17] and to evaluate the dominant character we need to consider aromaticity in addition. A qualitatively consideration of aromaticity uses the Hückel rule: a cycle with 4n+2 electron is aromatic, and stable, while a cycle with 4n electron is anti-aromatic, and unstable. Applied to mesomeric structures, the two labeled II (IIa and IIb) are aromatic and must be somehow more important than the anti-aromatic (III), and this explains why the exo-cyclic carbon atom is negatively charged. How important are aromatic structures compared to anti-aromatic actually requires a computational experiment (next section).The students can then be asked to do a similar qualitative study of the iminocyclopropene and the cyclopropenone molecules. They just have to substitute the exo-cyclic CH2 by more electronegative NH and O. They conclude that structures II are even more important in these two cases due to electronegativity.
The students are then asked to order the structures from the most important to the least important. If only the octet and charge separation rules are considered, structure I is the major structure, and the four others are equivalent because they all have a single charge separation. They are considered as minor structures because they violate the octet rule, and they all have the same weight because the charge separation is alike. At this stage the reasonning is qualitative. Neglecting any other consideration, we have wIIa = wIIb = wIIIa = wIIIb = w’ < wI. Moreover, the charge of the exo-cyclic carbon could be crudely estimated to be null because it corresponds roughly to the weighted average of its charge in each structure qC1=wI*0+ w’*(-1-1+1+1)=0. Hence the exo-cyclic carbon would be electrically neutral if only the octet rule and the charge separation rule are considered. However, the exo-cyclic carbon is experimentally known to be negatively charged, [17] and to evaluate the dominant character we need to consider aromaticity in addition. A qualitatively consideration of aromaticity uses the Hückel rule: a cycle with 4n+2 electron is aromatic, and stable, while a cycle with 4n electron is anti-aromatic, and unstable. Applied to mesomeric structures, the two labeled II (IIa and IIb) are aromatic and must be somehow more important than the anti-aromatic (III), and this explains why the exo-cyclic carbon atom is negatively charged. How important are aromatic structures compared to anti-aromatic actually requires a computational experiment (next section).The students can then be asked to do a similar qualitative study of the iminocyclopropene and the cyclopropenone molecules. They just have to substitute the exo-cyclic CH2 by more electronegative NH and O. They conclude that structures II are even more important in these two cases due to electronegativity.
3.2. Computational Experiment
First of all, HuLiS is used to build the methylenecyclopropene’s skeleton. The Lewis structures can be automatically generated, but a step-by-step construction is recommended, just after the prelab exercice. It is important that students check how the trust factor is modified when structures are added. The trust factor 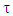 should be ideally close to 90%, the larger, the better. The Slider must be used to guarantee that the drawn structures are indeed included in the computation. The student are instructed to collect the data required to complete Table 1. To do so, they report the weight of each structure calculated by the Hückel projection method (HLP), and
should be ideally close to 90%, the larger, the better. The Slider must be used to guarantee that the drawn structures are indeed included in the computation. The student are instructed to collect the data required to complete Table 1. To do so, they report the weight of each structure calculated by the Hückel projection method (HLP), and 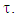 [12]
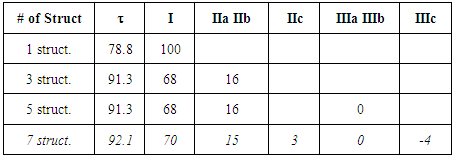
[12]Table 1. Trust factor
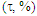 and weights (%) obtained for the methylenecyclopropene with some sets of resonant structures. The last set of seven structures includes redundant structures (IIc and IIIc) and weights (%) obtained for the methylenecyclopropene with some sets of resonant structures. The last set of seven structures includes redundant structures (IIc and IIIc)
 |
| |
|
In the second section, the students start from the methylenecyclopropene structure to make substitutions on the exocyclic carbon atom. They replace the C atom by respectively N and O atoms. Then, they should follow the same experimental protocol used in the first section and are asked to complete Table 2. The automatic generation can also be used. Bi-radical structures will pop up if the pref panel has not been adjusted (vide supra). If this is the case, the student can use the slider to see that three structures are enough to get a good and steady trust factor 
Table 2. Trust factor
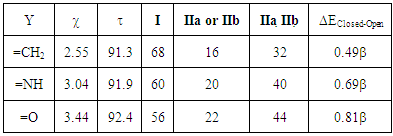
 and weights of the resonance structures of the molecules in the three-structure resonance scheme for iminocyclopropene (=NH substitution) and cyclopropenone (=O substitution); comparison to the parent molecule (=CH2); role of the electronegativity and weights of the resonance structures of the molecules in the three-structure resonance scheme for iminocyclopropene (=NH substitution) and cyclopropenone (=O substitution); comparison to the parent molecule (=CH2); role of the electronegativity
 of the heavy atom of the heavy atom
 |
| |
|
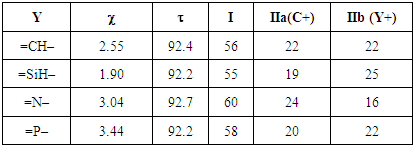
In the third section, the cyclopropenone is used as the starting molecule. A single substitution is performed, replacing a carbon ring atom, other than that bound to oxygen atom, successively by phosphorus, nitrogen, and silicon atoms (P, N and Si). [18, 19, 20] Also, we follow the protocol used previously to generate resonance structures and get their weights. At last, Table 3 can be completed.Table 3. The effect of replacing one ring carbon atom opposite to the carbonyl group in the cyclopropenone: weights of the main structures (wi) and Pauling electronegativity
 of the heavy atom of the heavy atom
 |
| |
|
Finally, students substitute one hydrogen atom of cyclopropenone by a fluorine atom, CH3 and PH2 group respectively. Then they generate all resonance structures and their corresponding weights. All the results should be summarized in Table 4.Table 4. Effect of replacing a hydrogen atom of the ring of. The electronegativity
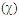 of the heavy atom is reminded of the heavy atom is reminded
 |
| |
|
4. Results and Discussion
In the first section and based on the results given on Table 1, the students form an initial point of view on the relative importance of each Lewis structure. It is usually said that structures that fulfill the octet rule are more likely than others; the computation actually confirms it. It can be seen in the weights for the three-structure computation (68/16/16 for the weights of I/IIa/IIb). The so-called aromatic structures account for about 32% of the electronic structure. When other structures, (particularly the anti-aromatic IIIa and IIIb) are included, their weight is close to zero, and the trust factor remains roughly the same. As it can be seen in Table 2, the more electronegative the exocyclic atom (=CH2<=NH<=O) the larger is the sum of the weights of the aromatic structures (IIa IIb), from 32 to 40, and up to 44% (cyclopropenone). The results lead the students to propose the following order of the weight of the aromatic structure for these three cases (Figure 4). This part illustrates that zwitterionic Lewis structures are more relevant when the negative charge is on an electronegative atom.  | Figure 4. The increasing order of the weights of the aromatic structures of cyclopropene derivatives |
For such carbonated cycle, the aromaticity is frequently computed at the Hückel level by the difference in energy between the closed and the opened ring as sketched in Figure 5. The value 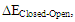 last column of Table 2 corresponds to this energy difference. A larger energy difference is obtained for the systems where aromatic structures have the larger weights.
last column of Table 2 corresponds to this energy difference. A larger energy difference is obtained for the systems where aromatic structures have the larger weights.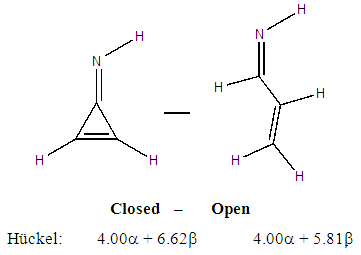 | Figure 5. Computation of the aromatic energy at the Hückel level for the NH substituted example (here the aromatic energy amounts to 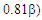 |
In the rest of the paper we only use the cyclopropenone, where the weights of the aromatic structures are the largest. For the next exercices, we replace one of the ring CH group by Y=SiH, N, or P. This creates a disymmetry so the zwitterionic resonance structures IIa and IIb become non-equivalent, and will have different weights, depending on the electronegativity of Y. A priori, if Y is more electronegative than C, then IIa should be favored over IIb. The two resonance structures that are concerned here are shown on Figure 6. 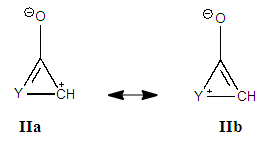 | Figure 6. Non equivalent resonance zwitterionic structures with a substitution in the cyclopropene ring |
The weights of the resonance structures are given in Table 3, together with the electronegativity of the Y atom and the trust factor obtained with HuLiS. The electroaffinity of the Y atom is indeed consistent with the weights of the structures: IIa is preferred over IIb when Y is more electronegative than the carbon (=N– case). The reversed order of weights is obtained for less electronegative cases (=SiH– and =P–). The effect is however quite small, and this part can be shortened in order to better fit in the allotted time.In section four, a donating substituent induces two new resonance structures (Figure 7, A, B). Those can be searched by students on a separated sheet of paper. Starting from I the two arrows of the electron pair mobility lead to A, and from A two arrows lead to B (Figure 8). These five structures are not difficult to order by lead when the simplest rules are applied (I is the major structure as it fulfills the octet rule and has no charge separation). Structure A and B both have the octet rule fulfilled. Structure B has the negative charge hosted on the most electronegative atom so it is more relevant than A. The two others do not fulfill the octet rule and should be minor structures with approximately the same weight.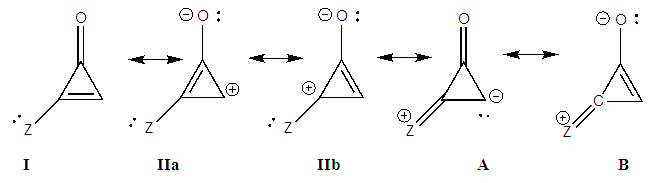 | Figure 7. Structures relative to the Z substitution in the cyclopropenone |
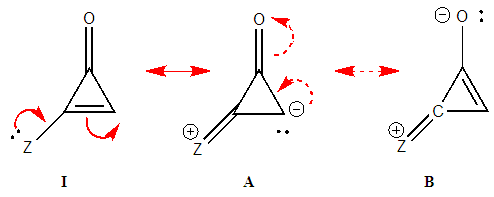 | Figure 8. Two-arrows electron-pair mobility in substituted cyclopropenone, structure A is obtained from I (and B from A) |
However, the aromaticity can again shuffle the qualitative guesses. Students are requested to return to HuLiS to do the actual computation of the weights. They shall fill Table 4, and compare the results to their estimates, in light of the aromaticity rule: cycles with 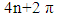 electrons are preferred. Note that the trust factor can be slightly below 90%. When writing resonant structures, small and even sometimes negative weights can appear. Negative weights can appear when two structures are redundant, as in the case of Z=F for instance. This redundancy comes from the shape of the πFC bond (Figure 9). Structures with negative weights should always be removed. Structures with small weights can also be removed. This is recommended because the resonance scheme is easier to read when it involves a small number of resonant structures. Meanwhile, it can be checked that the trust factor remains close to 90%. The smallest meaningful set of resonant structures is then I/ IIa/ B with weights 54/ 21/ 25 in the case of Z=F.
electrons are preferred. Note that the trust factor can be slightly below 90%. When writing resonant structures, small and even sometimes negative weights can appear. Negative weights can appear when two structures are redundant, as in the case of Z=F for instance. This redundancy comes from the shape of the πFC bond (Figure 9). Structures with negative weights should always be removed. Structures with small weights can also be removed. This is recommended because the resonance scheme is easier to read when it involves a small number of resonant structures. Meanwhile, it can be checked that the trust factor remains close to 90%. The smallest meaningful set of resonant structures is then I/ IIa/ B with weights 54/ 21/ 25 in the case of Z=F.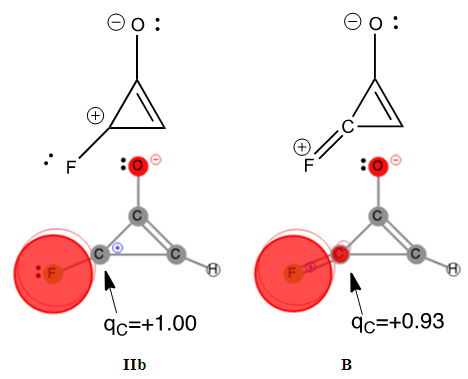 | Figure 9. Structures IIb and B of the F-substituted ring of cyclopropenone only differ by the: F–C+ (IIb) or F+=C (B) part. For IIb, the two π electrons are on the F atom while for B the two electrons are in principle in the π bond, hence shared by F and C atoms. However, this π bond in B is strongly polarized toward the Fluorine, and C remains essentially positive (qc=+0.93 e); only π electrons are represented here |
5. Conclusions
This paper described a laboratory work that shows some possibilities of HuLiS in the context of resonance. In addition to the weights of the Lewis structures, HuLiS also computes a trust factor that tells if the computation is reliable. It helps to tell if a structure is relevant.The mesomerism rules (octet, charge separation) are used to make predictions on the relevance of mesomeric structures for some molecules derivated from the methylenecyclopropene. When the molecules are drawn using the HuLiS program, their resonant structures can be automatically generated, or specifically drawn. Some structures that have 4n+2 electron in the cycle, have much larger weights than structures with 4n electrons. The structures with 4n+2 electron in the cycle can be called “aromatic structures” following the standard Hückel definition, and the 4n electron’s are “antiaromatic”. Electronegative substituents change the weights of the structures.
ACKNOWLEDGEMENTS
The authors acknowledge the community of HuLiS’ users for their continuous support.
Notes
#Note that the experiment used the HLP scheme throughout, rather than HL-CI, which remains in the program for historical reasons. HLP is the default method in HuLiS. Please see the manual for more details.1. (a) Ja. K. Syrkin, M. E. Dyatkina, Acta Physicochim. URSS 1946, 21, 641; (b) G. Berthier, B. Pullman Bull. Soc. Chim. France, 1949, 16, D457; (c) J. D. Roberts, A. Streitwieser, Jr., and C. M. Regan, J. Am. Chem. Soc. 1952, 74, 4579. 2. (a) A.S. Kende J. Am. Chem. Soc. 1963, 85, 1882 (b) S.W. Staley, T.D. Norden J. Am. Chem. Soc. 1984, 106, 3699. (b) W. E. Billups, L. Lin, E.W. Casserley J. Am. Chem. Soc. 1984, 106, 3698. (c) G. Maier, M. Hoppe, K. Lanz, P. Reisenauer, Tetrahedron Lett. 1984, 25, 5645.
Supplementaries of the Paper: This Part Contains Material for Students
Historical background: the methylenecyclopropene (or triafulvene) and its strong dipole moment was first theoretically predicted back in the early 50’s.1 Since then, many many many other great researchers have been interested by its electronic structure. They all confirmed its strong dipole moment, and have argued about its aromaticity. The first synthesis of a substituted methylenecyclopropene, has been reported in 1963, and numerous teams of talentuous chemists tried to synthetized the unsubstituted molecule. They only succeded in 1984, and the expected strong dipole moment was finally measured (about 2 D),2 consistent with theoretical predictions made about 30 years before.In this laboratory work we use the same Hückel method that was used by early theoreticians, and some recent developments are also used to complete our vision of this molecule.1. ObjectivesIn this lab weŸ Learn to how computational chemistry can be used to better understand chemistry conceptsŸ Differentiate the concepts of mesomerism and aromaticityŸ Look at the substitution effect on mesomerismThe last section (IV), about exocyclic substitution, leads to Lewis structure redundancy. It necessitates some advanced knowledge in overlap matrices. It is dedicated to students and teachers with a good expertise in quantum chemistry.2. Prior readingThe HuLiS applet calculates the weights of the resonance structures. It does not require any specific knowledge in computational chemistry and can be obtained freely from http://www.hulis.free.fr. HuLiS is available for all systems including smartphones, tablets, phablets, etc …. It can run in a web browser, as an on-line applet or as a stand-alone Java application, which is recommended.Preferences in HuLiS: Note that, in addition to the standard Lewis structures, HuLiS can automatically generates bi-radical structures. The preference panel controls this feature, and we recommend discarding the biradicals  The corresponding checkbox should be unchecked.
The corresponding checkbox should be unchecked.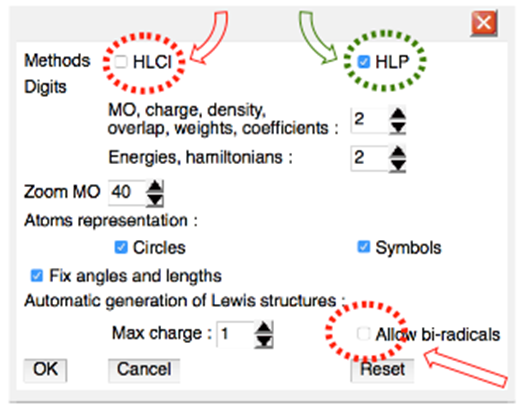 | Figure 1. Preference Panel in HuLiS |
Further reading: the HuLiS user’s manual can be found at: http://www.hulis.free.fr/download/HuLiS_Manuel_3_3_en.pdf3. Prelab exercise: make predictionsEstimated time to complete this exercise: 20 minutesŸ On a separated sheet of paper, draw the five different resonance structures of methylenecyclopropene (hint: in the first structure, the atoms are all formally neutral; in two other structures a formal negative charge is on C1, and in the two last a positive charge is formally on C1).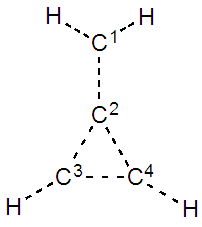 | Triafulvene’s structure |
Ÿ Considering the octet and charge separation rules, order the structures from the most important to the least important. Is the expected charge on the C1 atom null, positive, or negative?Ÿ Two structures fulfil the Hückel rule for aromaticity, while two other are considered as antiaromatic (4n+2 vs 4n electrons can be found in the C2C3C4 cycle). The aromatic structures can be expected to be more important that the anti-aromatic. Considering aromaticity, is the expected charge on the C1 atom null, positive, or negative?Ÿ When the exocyclic H2C1=C2 part is replaced by O1=C2 we obtain the methylenecyclopropenone (see below). Draw the five resonant structures in this case. And order them from the most important to the least important. Is the electronegative effect congruent with the aforementioned aromaticity effect? Do you expect the charge on the O1 atom to be more negative than in formaldehyde?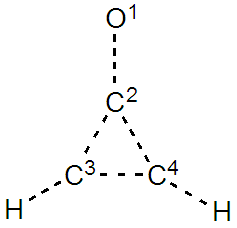 | Methylenecyclopropenone’s structure |
4. Computational experiment Estimated time to complete each section is 30 minutes. Nota: When a structure is drawn, it can be optimized by clicking on the  button on the left. It has no other effect than giving a nicer looking to the molecules. The calculations are done “on-the-fly”. They do not depend on the way molecules are drawn: only atoms’ connection matters. The nature of the link between the atoms (single or double bond) is automatically computed. Generally, a bond is neither single nor double but a mixture of them. Dashes are used to represent such a hybrid situation.SECTION I: Determination of the relative importance of Lewis structures1. Open the HuLiS applet by double clicking on the icone of hulis_v3.jar.2. Draw the methylenecyclopropene molecule using the “build” button. The calculation is done “on-the-fly”. There is negative π charge on the C1 atom. Comment this result with respect to your predictions. Nota: An output file showing the various steps of calculation and giving the main numerical results can be obtained from the left hand side
button on the left. It has no other effect than giving a nicer looking to the molecules. The calculations are done “on-the-fly”. They do not depend on the way molecules are drawn: only atoms’ connection matters. The nature of the link between the atoms (single or double bond) is automatically computed. Generally, a bond is neither single nor double but a mixture of them. Dashes are used to represent such a hybrid situation.SECTION I: Determination of the relative importance of Lewis structures1. Open the HuLiS applet by double clicking on the icone of hulis_v3.jar.2. Draw the methylenecyclopropene molecule using the “build” button. The calculation is done “on-the-fly”. There is negative π charge on the C1 atom. Comment this result with respect to your predictions. Nota: An output file showing the various steps of calculation and giving the main numerical results can be obtained from the left hand side  button. The π atomic charges are indicated at the end (fourth part). The unit is the atomic unit: -1 indicates an excess of one electron.3. Generate all the resonance structures of methylenecyclopropene using the “Generate All” button. They are labelled
button. The π atomic charges are indicated at the end (fourth part). The unit is the atomic unit: -1 indicates an excess of one electron.3. Generate all the resonance structures of methylenecyclopropene using the “Generate All” button. They are labelled 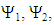 etc and appear in thumbs separated from the Hückel results (which is labeled
etc and appear in thumbs separated from the Hückel results (which is labeled 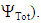 Use the slider on the right to see all the thumbs, and compare the structures automatically generated to yours (that you have drawn in the prelab exercise) and finally label them I, II, III, etc. Nota 1: The vertical slider on the right can be used to select the most relevant structures. Structures can also be removed, with
Use the slider on the right to see all the thumbs, and compare the structures automatically generated to yours (that you have drawn in the prelab exercise) and finally label them I, II, III, etc. Nota 1: The vertical slider on the right can be used to select the most relevant structures. Structures can also be removed, with  button. If necessary, new resonance structures can be added using the create button of the right panel.Nota 2: The right hand side
button. If necessary, new resonance structures can be added using the create button of the right panel.Nota 2: The right hand side  button opens the Lewis’ results as text. 4. Fill Table 1 with the trust factor
button opens the Lewis’ results as text. 4. Fill Table 1 with the trust factor 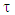 and the weights of each structure as obtained with different sets of resonant structures. Find the smallest most relevant set on the basis of the trust factor
and the weights of each structure as obtained with different sets of resonant structures. Find the smallest most relevant set on the basis of the trust factor 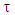 . This factor
. This factor 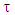 should be preferably larger than about 90%.
should be preferably larger than about 90%.Table 1. Trust factor and weights of the resonance structures for methylenecyclopropene
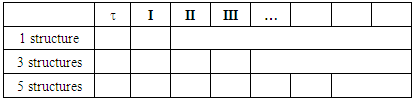 |
| |
|
SECTION II: Substitution of the X exocyclic atom.1. To modify the molecule of the previous calculation you first have to erase all previous resonance structures, then select the change button in the Hückel panel and modify the C1 atom. In this part you first work with the =NH substitution (not -NH2). The C=O substitution is to be studied after.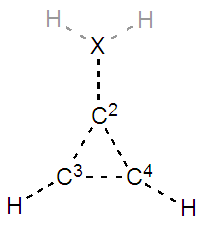 2. Fill Table 2 with the trust factor and the weight of the resonance structures of the molecules in their best three-structure resonance scheme. Do so for iminocyclopropene (=NH substitution) and for cyclopropenone (=O substitution). Remind the values obtained for the parent molecule methylencyclopropene (=CH2). EN stands for, electronegativity. Discuss the results in light of the electronegativity of the exocyclic atom.
2. Fill Table 2 with the trust factor and the weight of the resonance structures of the molecules in their best three-structure resonance scheme. Do so for iminocyclopropene (=NH substitution) and for cyclopropenone (=O substitution). Remind the values obtained for the parent molecule methylencyclopropene (=CH2). EN stands for, electronegativity. Discuss the results in light of the electronegativity of the exocyclic atom.Table 2. Trust factor and weights when the exocyclic carbon of the methylenecyclopropene is substituted by a more electronegative atom (the electronegativity of the heavy atom is reminded:
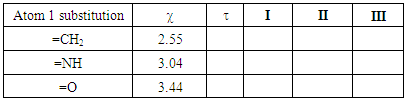 |
| |
|
3. We can attribute to a molecule a resonance energy, defined as the (electronic) energy difference between the molecule and its hypothetical localized resonance structure. Moreover, the aromatic energy can also be defined as the energy difference between the closed and the open molecule (Figure 2). The energy of a molecule has the form 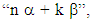 and is displayed in HuLiS as Etot on the left hand-side panel, just above the results button
and is displayed in HuLiS as Etot on the left hand-side panel, just above the results button  have a negative value). When you erase a bond (for instance C2- -C4), two H atoms are automatically added to the delocalized structure of the molecule (see Figure 2). Fill Table 2bis and comment on the aromatic energy for the three cases with respect to electronegativity. Can you connect your findings with the weights of the aromatic structures obtained in Table 2?
have a negative value). When you erase a bond (for instance C2- -C4), two H atoms are automatically added to the delocalized structure of the molecule (see Figure 2). Fill Table 2bis and comment on the aromatic energy for the three cases with respect to electronegativity. Can you connect your findings with the weights of the aromatic structures obtained in Table 2?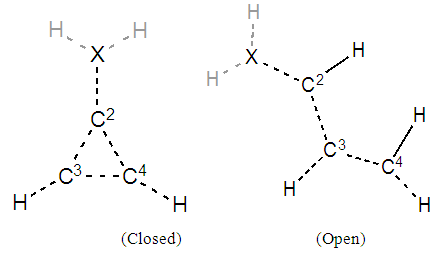 | Figure 2. To compute the aromatic energy, consider closed vs. open delocalized structures |
Table 2bis. Aromatic energy calculation for the X substitutions. The Pauling electronegativity is reminded
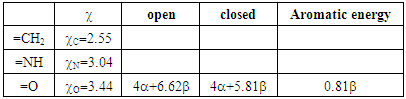 |
| |
|
SECTION III: Replacing one ring atom on the aromatic structures 1. From the cyclopropenone (=O substitution), substitute a carbon atom of the ring (not the one bound to oxygen) by a silicon atom. For instance do it at the C3 position.  2. Generate the best three-structure resonance scheme and fill Table 3. Be careful that in IIb the positive charge is on the Y atom, while in IIa it is on C4.3. These substitutions induce a disymmetry. Discuss the results with respect to the difference in electronegativity of Si and C.
2. Generate the best three-structure resonance scheme and fill Table 3. Be careful that in IIb the positive charge is on the Y atom, while in IIa it is on C4.3. These substitutions induce a disymmetry. Discuss the results with respect to the difference in electronegativity of Si and C. Table 3. Cyclopropenone with a Y substitution at the C3 position. Pauling electronegativity (χ) of the heavy atom is reminded
 |
| |
|
SECTION IV: Replacing the H atom of C3 by Z, an electrodonating atom We still use the cyclopropenone, and two substituents are considered Z=F and Z=NH2.1. Preliminary paper exercise: give the two new structures due to the donating substituent when Z=F. Indicate the mobility of the pair of electrons by arrows. Label these structures A and B, and order them by lead. 2. Computer exercise: draw the cyclopropenone on the screen, and substitute a hydrogen atom with the Z=F (Fluorine) atom. Generate all resonance structures, and selecte a five-structure set to fill Table 4. Note that IIa has now a very small weight, and that
2. Computer exercise: draw the cyclopropenone on the screen, and substitute a hydrogen atom with the Z=F (Fluorine) atom. Generate all resonance structures, and selecte a five-structure set to fill Table 4. Note that IIa has now a very small weight, and that  does not change if IIa is removed (button
does not change if IIa is removed (button  ). This is because this structure and another one (A or B) are alike. This can be seen in the overlap matrix with the Lewis’
). This is because this structure and another one (A or B) are alike. This can be seen in the overlap matrix with the Lewis’  button. Let’s call SIJ the “overlap” between two structures I and J. In the overlap matrix, SIJ is located at the line labeled “I” and at the column “J”. It is a number, a real, bounded between –1 and +1. When SIJ = +1, the two structures I and J are exactly equal (I=J). When SIJ = –1, the two structures I and J are exactly opposite (I= –J), and when SIJ=0, the two are totally different, we say that they are “orthogonal”. Here two structures have SIJ=0.97, so they are almost equal and we can remove one of them. Fill Table 4 also for the NH2 substituent.
button. Let’s call SIJ the “overlap” between two structures I and J. In the overlap matrix, SIJ is located at the line labeled “I” and at the column “J”. It is a number, a real, bounded between –1 and +1. When SIJ = +1, the two structures I and J are exactly equal (I=J). When SIJ = –1, the two structures I and J are exactly opposite (I= –J), and when SIJ=0, the two are totally different, we say that they are “orthogonal”. Here two structures have SIJ=0.97, so they are almost equal and we can remove one of them. Fill Table 4 also for the NH2 substituent.Table 4. Electro donating substituent in the cyclopropenone: trust factor and weights. The electronegativity (χ) of the heavy atom is reminded
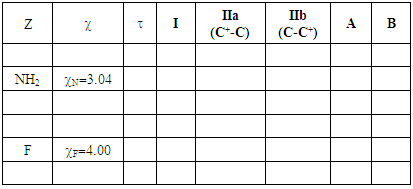 |
| |
|
References
| [1] | Clayden, J.; Greeves, N.; Warren, S. Organic Chemistry, 2 edition.; OUP Oxford: Oxford; New YorK, 2012. |
| [2] | Schleyer, P. von R. Introduction: Aromaticity. Chem. Rev. 2001, 101 (5), 1115–1118. |
| [3] | Fallah-Bagher-Shaidaei, H.; Wannere, C. S.; Corminboeuf, C.; Puchta, R.; Schleyer, P. v. R. Which NICS Aromaticity Index for Planar π Rings Is Best? Org. Lett. 2006, 8 (5), 863–866. |
| [4] | Wang, Y.; Fernández, I.; Duvall, M.; Wu, J. I.-C.; Li, Q.; Frenking, G.; Schleyer, P. von R. Consistent Aromaticity Evaluations of Methylenecyclopropene Analogues. J. Org. Chem. 2010, 75 (23), 8252–8257. |
| [5] | Stanger, A. What Is… Aromaticity: A Critique of the Concept of Aromaticity—can It Really Be Defined? Chem. Commun. 2009, No. 15, 1939. |
| [6] | Wang, H.-J.; Schleyer, P. v. R.; Wu, J. I.; Wang, Y.; Wang, H.-J. A Study of Aromatic Three Membered Rings. Int. J. Quantum Chem. 2011, 111 (5), 1031–1038. |
| [7] | Breslow, R. SYNTHESIS OF THES-TRIPHENYLCYCLOPROPENYL CATION. J. Am. Chem. Soc. 1957, 79 (19), 5318–5318. |
| [8] | Breslow, R.; Brown, J.; Gajewski, J. J. Antiaromaticity of Cyclopropenyl Anions. J. Am. Chem. Soc. 1967, 89 (17), 4383–4390. |
| [9] | Breslow, R. Antiaromaticity. Acc. Chem. Res. 1973, 6 (12), 393–398. |
| [10] | Breslow, R. A Life in Physical Organic Chemistry. In The Foundations of Physical Organic Chemistry: Fifty Years of the James Flack Norris Award; Strom, E. T., Mainz, V. V., Eds.; American Chemical Society, Series Ed.; American Chemical Society: Washington, DC, 2015; Vol. 1209, pp 61–76. |
| [11] | Carissan, Y.; Hagebaum-Reignier, D.; Goudard, N.; Humbel, S. HuLiS Code: Lewis Embedded in Hückel Theory; 2008. |
| [12] | Carissan, Y.; Hagebaum-Reignier, D.; Goudard, N.; Humbel, S. Hückel-Lewis Projection Method: A “Weights Watcher” for Mesomeric Structures. J. Phys. Chem. A 2008, 112 (50), 13256–13262. |
| [13] | Rauk, A.; Cannings, R. Interactive SHMO | Arvi Rauk -- Orbitals, Inc. | University of Calgary http://www.ucalgary.ca/rauk/shmo (accessed Mar 31, 2016). |
| [14] | Humbel, S. Getting the Weights of Lewis Structures out of Huckel Theory: Huckel-Lewis Configuration Interaction (HL-Cl). J. Chem. Educ. 2007, 84 (6), 1056–1061. |
| [15] | Hagebaum-Reignier, D.; Girardi, R.; Carissan, Y.; Humbel, S. Hückel Theory for Lewis Structures: Hückel–Lewis Configuration Interaction (HL-CI). J. Mol. Struct. THEOCHEM 2007, 817 (1–3), 99–109. |
| [16] | Carissan, Y.; Goudard, N.; Hagebaum-Reignier, D.; Humbel, S. Localized Structures at the Hückel Level, a Hückel-Derived Valence Bond Method. In Applications of Topological Methods in Molecular Chemistry; Challenges and Advances in Computational Chemistry and Physics; Chauvin, R., Lepetit, C., Silvi, B., Alikhani, E.: Cham, 2016; Vol. 22, pp 337–360. |
| [17] | Norden, T. D.; Staley, S. W.; Taylor, W. H.; Harmony, M. D. Electronic Character of Methylenecyclopropene: Microwave Spectrum, Structure, and Dipole Moment. J. Am. Chem. Soc. 1986, 108 (25), 7912–7918. |
| [18] | Veszprémi, T.; Takahashi, M.; Ogasawara, J.; Sakamoto, K.; Kira, M. An Ab Initio MO Study of Structure and Reactivity of 4-Silatriafulvene. J. Am. Chem. Soc. 1998, 120 (10), 2408–2414. |
| [19] | Höltzl, T.; Nguyen, M. T.; Veszprémi, T. Mono-, Di-, Tri- and Tetraphosphatriafulvenes: Electronic Structure and Aromaticity. J. Mol. Struct. THEOCHEM 2007, 811 (1–3), 27–35. |
| [20] | Saebø, S.; Stroble, S.; Collier, W.; Ethridge, R.; Wilson, Z.; Tahai, M.; Pittman, C. U. Aromatic Character of Tria- and Pentafulvene and Their Exocyclic Si, Ge, and Sn Derivatives. An Ab Initio Study. J. Org. Chem. 1999, 64 (4), 1311–1318. |





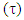 associated to the Lewis structures combination is computed as well. It is defined as the overlap between the Hückel wave function, which is the reference wave function, and the combination of Lewis Structures. When
associated to the Lewis structures combination is computed as well. It is defined as the overlap between the Hückel wave function, which is the reference wave function, and the combination of Lewis Structures. When 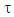 is larger than 90%, we consider that the combination of the Lewis structures adequately mimics Hückel’s. A low trust factor
is larger than 90%, we consider that the combination of the Lewis structures adequately mimics Hückel’s. A low trust factor 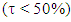 should be considered as a warning that the structures are not adequately selected. The user must then add new (and appropriate) structures. New Lewis structures can be add/rmodified with the mouse. The overlap of a structure with the Hückel wavefunction defines the relevance of the Lewis structure. A slider is used to select most relevant structures. Orbitals and Hückel energies are computed on the fly, and energy levels appear on a ladder, to the right of the central panel. When an energy level is selected, the corresponding orbital is plotted. If the central panel displays a Lewis structure, all the orbitals obey the localization constraint, as displayed in Figure 1a. If the central panel displays the delocalized structure, the orbitals are delocalized, as in regular Hückel computations. In the Java version the Lewis structures are in thumbs at the top, with just the label of the structure written on. By a click on a thumb, the user displays the corresponding Lewis structure (Figure 1a). A vertical slider is displayed in the Lewis panel. It can be used to select the most relevant set of Lewis structures among a basis of Lewis structures. The coefficient and the weight of each structure are displayed together with its energy above the slider. These numbers can be obtained through the results button of the Lewis panel. How HuLiS works has been described elsewhere. [12, 14, 15, 16] In the version for mobiles there is a graphical summary at the bottom, with stamps of each structure. The boxes are blue for the delocalized structure and orange for the Lewis’. These stamps replace the thumb, and are used to switch between structures. We put the slider above the stamps with a red round shape cursor.
should be considered as a warning that the structures are not adequately selected. The user must then add new (and appropriate) structures. New Lewis structures can be add/rmodified with the mouse. The overlap of a structure with the Hückel wavefunction defines the relevance of the Lewis structure. A slider is used to select most relevant structures. Orbitals and Hückel energies are computed on the fly, and energy levels appear on a ladder, to the right of the central panel. When an energy level is selected, the corresponding orbital is plotted. If the central panel displays a Lewis structure, all the orbitals obey the localization constraint, as displayed in Figure 1a. If the central panel displays the delocalized structure, the orbitals are delocalized, as in regular Hückel computations. In the Java version the Lewis structures are in thumbs at the top, with just the label of the structure written on. By a click on a thumb, the user displays the corresponding Lewis structure (Figure 1a). A vertical slider is displayed in the Lewis panel. It can be used to select the most relevant set of Lewis structures among a basis of Lewis structures. The coefficient and the weight of each structure are displayed together with its energy above the slider. These numbers can be obtained through the results button of the Lewis panel. How HuLiS works has been described elsewhere. [12, 14, 15, 16] In the version for mobiles there is a graphical summary at the bottom, with stamps of each structure. The boxes are blue for the delocalized structure and orange for the Lewis’. These stamps replace the thumb, and are used to switch between structures. We put the slider above the stamps with a red round shape cursor.
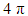 electrons.
electrons.
 The students are then asked to order the structures from the most important to the least important. If only the octet and charge separation rules are considered, structure I is the major structure, and the four others are equivalent because they all have a single charge separation. They are considered as minor structures because they violate the octet rule, and they all have the same weight because the charge separation is alike. At this stage the reasonning is qualitative. Neglecting any other consideration, we have wIIa = wIIb = wIIIa = wIIIb = w’ < wI. Moreover, the charge of the exo-cyclic carbon could be crudely estimated to be null because it corresponds roughly to the weighted average of its charge in each structure qC1=wI*0+ w’*(-1-1+1+1)=0. Hence the exo-cyclic carbon would be electrically neutral if only the octet rule and the charge separation rule are considered. However, the exo-cyclic carbon is experimentally known to be negatively charged, [17] and to evaluate the dominant character we need to consider aromaticity in addition. A qualitatively consideration of aromaticity uses the Hückel rule: a cycle with 4n+2 electron is aromatic, and stable, while a cycle with 4n electron is anti-aromatic, and unstable. Applied to mesomeric structures, the two labeled II (IIa and IIb) are aromatic and must be somehow more important than the anti-aromatic (III), and this explains why the exo-cyclic carbon atom is negatively charged. How important are aromatic structures compared to anti-aromatic actually requires a computational experiment (next section).The students can then be asked to do a similar qualitative study of the iminocyclopropene and the cyclopropenone molecules. They just have to substitute the exo-cyclic CH2 by more electronegative NH and O. They conclude that structures II are even more important in these two cases due to electronegativity.
The students are then asked to order the structures from the most important to the least important. If only the octet and charge separation rules are considered, structure I is the major structure, and the four others are equivalent because they all have a single charge separation. They are considered as minor structures because they violate the octet rule, and they all have the same weight because the charge separation is alike. At this stage the reasonning is qualitative. Neglecting any other consideration, we have wIIa = wIIb = wIIIa = wIIIb = w’ < wI. Moreover, the charge of the exo-cyclic carbon could be crudely estimated to be null because it corresponds roughly to the weighted average of its charge in each structure qC1=wI*0+ w’*(-1-1+1+1)=0. Hence the exo-cyclic carbon would be electrically neutral if only the octet rule and the charge separation rule are considered. However, the exo-cyclic carbon is experimentally known to be negatively charged, [17] and to evaluate the dominant character we need to consider aromaticity in addition. A qualitatively consideration of aromaticity uses the Hückel rule: a cycle with 4n+2 electron is aromatic, and stable, while a cycle with 4n electron is anti-aromatic, and unstable. Applied to mesomeric structures, the two labeled II (IIa and IIb) are aromatic and must be somehow more important than the anti-aromatic (III), and this explains why the exo-cyclic carbon atom is negatively charged. How important are aromatic structures compared to anti-aromatic actually requires a computational experiment (next section).The students can then be asked to do a similar qualitative study of the iminocyclopropene and the cyclopropenone molecules. They just have to substitute the exo-cyclic CH2 by more electronegative NH and O. They conclude that structures II are even more important in these two cases due to electronegativity.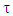 should be ideally close to 90%, the larger, the better. The Slider must be used to guarantee that the drawn structures are indeed included in the computation. The student are instructed to collect the data required to complete Table 1. To do so, they report the weight of each structure calculated by the Hückel projection method (HLP), and
should be ideally close to 90%, the larger, the better. The Slider must be used to guarantee that the drawn structures are indeed included in the computation. The student are instructed to collect the data required to complete Table 1. To do so, they report the weight of each structure calculated by the Hückel projection method (HLP), and 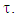 [12]
[12]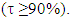

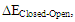 last column of Table 2 corresponds to this energy difference. A larger energy difference is obtained for the systems where aromatic structures have the larger weights.
last column of Table 2 corresponds to this energy difference. A larger energy difference is obtained for the systems where aromatic structures have the larger weights.
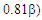



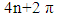 electrons are preferred. Note that the trust factor can be slightly below 90%. When writing resonant structures, small and even sometimes negative weights can appear. Negative weights can appear when two structures are redundant, as in the case of Z=F for instance. This redundancy comes from the shape of the πFC bond (Figure 9). Structures with negative weights should always be removed. Structures with small weights can also be removed. This is recommended because the resonance scheme is easier to read when it involves a small number of resonant structures. Meanwhile, it can be checked that the trust factor remains close to 90%. The smallest meaningful set of resonant structures is then I/ IIa/ B with weights 54/ 21/ 25 in the case of Z=F.
electrons are preferred. Note that the trust factor can be slightly below 90%. When writing resonant structures, small and even sometimes negative weights can appear. Negative weights can appear when two structures are redundant, as in the case of Z=F for instance. This redundancy comes from the shape of the πFC bond (Figure 9). Structures with negative weights should always be removed. Structures with small weights can also be removed. This is recommended because the resonance scheme is easier to read when it involves a small number of resonant structures. Meanwhile, it can be checked that the trust factor remains close to 90%. The smallest meaningful set of resonant structures is then I/ IIa/ B with weights 54/ 21/ 25 in the case of Z=F.
 The corresponding checkbox should be unchecked.
The corresponding checkbox should be unchecked.


 button on the left. It has no other effect than giving a nicer looking to the molecules. The calculations are done “on-the-fly”. They do not depend on the way molecules are drawn: only atoms’ connection matters. The nature of the link between the atoms (single or double bond) is automatically computed. Generally, a bond is neither single nor double but a mixture of them. Dashes are used to represent such a hybrid situation.SECTION I: Determination of the relative importance of Lewis structures1. Open the HuLiS applet by double clicking on the icone of hulis_v3.jar.2. Draw the methylenecyclopropene molecule using the “build” button. The calculation is done “on-the-fly”. There is negative π charge on the C1 atom. Comment this result with respect to your predictions. Nota: An output file showing the various steps of calculation and giving the main numerical results can be obtained from the left hand side
button on the left. It has no other effect than giving a nicer looking to the molecules. The calculations are done “on-the-fly”. They do not depend on the way molecules are drawn: only atoms’ connection matters. The nature of the link between the atoms (single or double bond) is automatically computed. Generally, a bond is neither single nor double but a mixture of them. Dashes are used to represent such a hybrid situation.SECTION I: Determination of the relative importance of Lewis structures1. Open the HuLiS applet by double clicking on the icone of hulis_v3.jar.2. Draw the methylenecyclopropene molecule using the “build” button. The calculation is done “on-the-fly”. There is negative π charge on the C1 atom. Comment this result with respect to your predictions. Nota: An output file showing the various steps of calculation and giving the main numerical results can be obtained from the left hand side  button. The π atomic charges are indicated at the end (fourth part). The unit is the atomic unit: -1 indicates an excess of one electron.3. Generate all the resonance structures of methylenecyclopropene using the “Generate All” button. They are labelled
button. The π atomic charges are indicated at the end (fourth part). The unit is the atomic unit: -1 indicates an excess of one electron.3. Generate all the resonance structures of methylenecyclopropene using the “Generate All” button. They are labelled 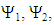 etc and appear in thumbs separated from the Hückel results (which is labeled
etc and appear in thumbs separated from the Hückel results (which is labeled  Use the slider on the right to see all the thumbs, and compare the structures automatically generated to yours (that you have drawn in the prelab exercise) and finally label them I, II, III, etc. Nota 1: The vertical slider on the right can be used to select the most relevant structures. Structures can also be removed, with
Use the slider on the right to see all the thumbs, and compare the structures automatically generated to yours (that you have drawn in the prelab exercise) and finally label them I, II, III, etc. Nota 1: The vertical slider on the right can be used to select the most relevant structures. Structures can also be removed, with  button. If necessary, new resonance structures can be added using the create button of the right panel.Nota 2: The right hand side
button. If necessary, new resonance structures can be added using the create button of the right panel.Nota 2: The right hand side  button opens the Lewis’ results as text. 4. Fill Table 1 with the trust factor
button opens the Lewis’ results as text. 4. Fill Table 1 with the trust factor 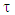 and the weights of each structure as obtained with different sets of resonant structures. Find the smallest most relevant set on the basis of the trust factor
and the weights of each structure as obtained with different sets of resonant structures. Find the smallest most relevant set on the basis of the trust factor 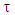 . This factor
. This factor 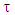 should be preferably larger than about 90%.
should be preferably larger than about 90%. 2. Fill Table 2 with the trust factor and the weight of the resonance structures of the molecules in their best three-structure resonance scheme. Do so for iminocyclopropene (=NH substitution) and for cyclopropenone (=O substitution). Remind the values obtained for the parent molecule methylencyclopropene (=CH2). EN stands for, electronegativity. Discuss the results in light of the electronegativity of the exocyclic atom.
2. Fill Table 2 with the trust factor and the weight of the resonance structures of the molecules in their best three-structure resonance scheme. Do so for iminocyclopropene (=NH substitution) and for cyclopropenone (=O substitution). Remind the values obtained for the parent molecule methylencyclopropene (=CH2). EN stands for, electronegativity. Discuss the results in light of the electronegativity of the exocyclic atom.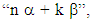 and is displayed in HuLiS as Etot on the left hand-side panel, just above the results button
and is displayed in HuLiS as Etot on the left hand-side panel, just above the results button 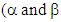 have a negative value). When you erase a bond (for instance C2- -C4), two H atoms are automatically added to the delocalized structure of the molecule (see Figure 2). Fill Table 2bis and comment on the aromatic energy for the three cases with respect to electronegativity. Can you connect your findings with the weights of the aromatic structures obtained in Table 2?
have a negative value). When you erase a bond (for instance C2- -C4), two H atoms are automatically added to the delocalized structure of the molecule (see Figure 2). Fill Table 2bis and comment on the aromatic energy for the three cases with respect to electronegativity. Can you connect your findings with the weights of the aromatic structures obtained in Table 2?
 2. Generate the best three-structure resonance scheme and fill Table 3. Be careful that in IIb the positive charge is on the Y atom, while in IIa it is on C4.3. These substitutions induce a disymmetry. Discuss the results with respect to the difference in electronegativity of Si and C.
2. Generate the best three-structure resonance scheme and fill Table 3. Be careful that in IIb the positive charge is on the Y atom, while in IIa it is on C4.3. These substitutions induce a disymmetry. Discuss the results with respect to the difference in electronegativity of Si and C.  2. Computer exercise: draw the cyclopropenone on the screen, and substitute a hydrogen atom with the Z=F (Fluorine) atom. Generate all resonance structures, and selecte a five-structure set to fill Table 4. Note that IIa has now a very small weight, and that
2. Computer exercise: draw the cyclopropenone on the screen, and substitute a hydrogen atom with the Z=F (Fluorine) atom. Generate all resonance structures, and selecte a five-structure set to fill Table 4. Note that IIa has now a very small weight, and that  does not change if IIa is removed (button
does not change if IIa is removed (button  ). This is because this structure and another one (A or B) are alike. This can be seen in the overlap matrix with the Lewis’
). This is because this structure and another one (A or B) are alike. This can be seen in the overlap matrix with the Lewis’  button. Let’s call SIJ the “overlap” between two structures I and J. In the overlap matrix, SIJ is located at the line labeled “I” and at the column “J”. It is a number, a real, bounded between –1 and +1. When SIJ = +1, the two structures I and J are exactly equal (I=J). When SIJ = –1, the two structures I and J are exactly opposite (I= –J), and when SIJ=0, the two are totally different, we say that they are “orthogonal”. Here two structures have SIJ=0.97, so they are almost equal and we can remove one of them. Fill Table 4 also for the NH2 substituent.
button. Let’s call SIJ the “overlap” between two structures I and J. In the overlap matrix, SIJ is located at the line labeled “I” and at the column “J”. It is a number, a real, bounded between –1 and +1. When SIJ = +1, the two structures I and J are exactly equal (I=J). When SIJ = –1, the two structures I and J are exactly opposite (I= –J), and when SIJ=0, the two are totally different, we say that they are “orthogonal”. Here two structures have SIJ=0.97, so they are almost equal and we can remove one of them. Fill Table 4 also for the NH2 substituent. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML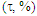 and weights (%) obtained for the methylenecyclopropene with some sets of resonant structures. The last set of seven structures includes redundant structures (IIc and IIIc)
and weights (%) obtained for the methylenecyclopropene with some sets of resonant structures. The last set of seven structures includes redundant structures (IIc and IIIc) 
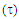 and weights of the resonance structures of the molecules in the three-structure resonance scheme for iminocyclopropene (=NH substitution) and cyclopropenone (=O substitution); comparison to the parent molecule (=CH2); role of the electronegativity
and weights of the resonance structures of the molecules in the three-structure resonance scheme for iminocyclopropene (=NH substitution) and cyclopropenone (=O substitution); comparison to the parent molecule (=CH2); role of the electronegativity 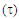 of the heavy atom
of the heavy atom
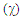 of the heavy atom
of the heavy atom
 of the heavy atom is reminded
of the heavy atom is reminded