Gary W. Breton
Department of Chemistry and Biochemistry, Berry College, Mount Berry, USA
Correspondence to: Gary W. Breton , Department of Chemistry and Biochemistry, Berry College, Mount Berry, USA.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We describe a simple homemade polarimeter that can be conveniently used in the classroom to demonstrate the application of polarized light towards the detection of chirality. The basic theory behind the operation of a polarimeter is discussed. Example data for (+)-α-pinene and (–)-β-pinene are included.
Keywords:
Chirality, Polarimeter, Polarized light, Pinene, Classroom demonstration
Cite this paper: Gary W. Breton , An Inexpensive Homemade Polarimeter for Demonstration Use in the Classroom, Journal of Laboratory Chemical Education, Vol. 3 No. 1, 2015, pp. 7-11. doi: 10.5923/j.jlce.20150301.02.
1. Introduction
Chirality is an important topic in any introductory Organic Chemistry course. Typically included in the discussion of chirality is the use of a polarimeter to determine the optical rotation of chiral compounds. Although the theory behind polarimeters is quite simple, we have found that undergraduate students often have a difficult time conceptualizing how the angle of rotation of polarized light is measured in practice. While commercial polarimeters can be purchased, they are expensive and not particularly conducive to being used to demonstrate their application for the detection of chirality in a classroom setting. Several homemade polarimetershave been reported in the literature [1], and some have been specifically designed for use in classroom demonstrations [2]. However, we found the designs for the reported classroom demonstration units to be either inconvenient for easy setup in the classroom, or much more involved than we thought necessary. We decided to design and construct our own polarimeter with the aim of making it simple to build, convenient to use in the classroom, and inexpensive.
2. Basic Theory of a Polarimeter
The basis components of a polarimeter are two polarizing lenses capping a sample tube (A in Scheme 1). Incoming nonpolarized light (to the left of the sample tube in A) is polarized as it passes through the first polarizing lens and into the empty sample tube. The polarized light is unperturbed by the empty tube and emerges in the same plane in which it was originally polarized. Thus bright light is observed at the other end of the tube. In B, the polarized light is passed through the sample tube filled with an optically inactive substance (e.g., water). Optically inactive substances do not affect the plane of polarized light and it emerges from the polarimeterthe same as if the sample tube were empty. In C, however, the sample tube is filled with an optically active substance (i.e., a single enantiomer of a chiral molecule, or a scalemic mixture of enantiomers). In this case, the plane of polarized light is rotated as it passes through the sample tube. If one is viewing through the second lens, the light does not pass through the lens readily. Upon rotation of the lens (either in the dextrorotatory [i.e., +] or levoratorory [i.e., –]direction) the second lens eventually lines up with the plane of polarized light and maximum transmittance of light is again observed. The resulting angle of rotation is called the “observed rotation”. To convert the observed rotation to a standardized specific rotation, at the very minimum the length of the sample tube (in dm) and concentration of the sample (in g/mL) need to be taken into account (equation 1):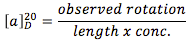 | (1) |
Standardardized specific rotations also require that the light source be that of a deuterium lamp (the “D” in equation 1) and that measurements be made at 20°C. While we are able to easily account for path length and the concentration of the sample when using our constructed polarimeter, temperature and light source are nonstandard and thus it is expected that values only close to literature values will be obtained (vide infra). However, for the purposes of classroom demonstration, this is acceptable.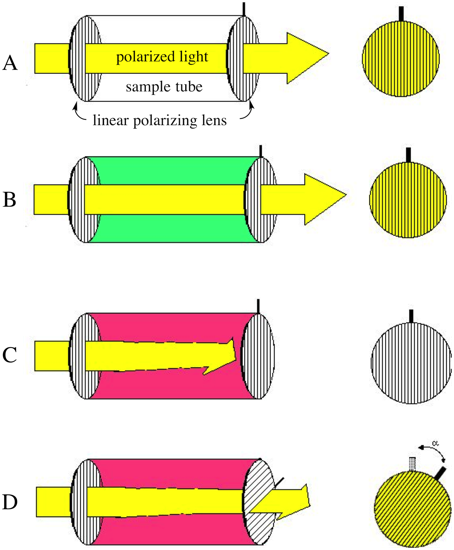 | Figure 1. Basic componentry and theory of a working polarimeter |
3. Construction of the Polarimeter
The essential items needed for construction of the polarimeter are displayed in Figure 2. Two inexpensive pieces of linear polarizing film, a 100 mL beaker (5 x 7.5 cm, preferably without a pouring lip at the top), two pieces of 2” i.d. PVC pipe cut to length (the bottom piece at ~7 cm and the upper piece at ~1 cm using a standard miter saw), and aprotractor face printed out on suitable card stock. The sources for these items can be found in reference [3]. The 7 cm high “body” of the polarimeter is cut slightly shorter than the 7.5 cm beaker “sample tube” so that the sample tube can be conveniently added to or removed from the body without spilling the contents.  | Figure 2. Essential items required for construction of the polarimeter |
First, the outer face of the protractor was cut out from the card stock while temporarily maintaining the inner circle. The PVC body was centered on the protractor face and, from the inside of the PVC pipe, dark marks were made at the crosshairs where the PVC and crosshairs touched (Figure 3A). The card stock was then flipped over and, using the dark marks that showed through the cardstock, the PVC body was glued to the backside center of the protractor face (Figure 3B). After allowing time for the glue to dry the center of the protractor face was removed using a razor blade (Figure 3C). The bottom of the PVC body was then securely glued to one of the squares of polarized film and the excess film trimmed (Figure 4A). A piece of film was similarly attached to one side of the top piece (1 cm length) of PVC (Figure 4B). The top piece of PVC (polarized film towards the bottom) was centered on top of the polarimeter body and the apparatus placed on top of a light source (e.g. an overhead projector). The top piece was rotated until there was a minimum of light transferred through the top (i.e., so that the two polarizers were at 90° relative to one another). A mark was made on the top PVC piece at the 0° position relative to the protractor face. A small hole was drilled at this position and a piece of wire glued into the hole so that the top piece could act as an indicator dial from which to read rotation measurements (figure 4C). The complete assembly of the polarimeter is displayed in Figure 5. | Figure 3. (A) Centering the PVC body onto the face of the protractor; (B) Gluing the PVC body to the back of the protractor face; (C) PVC body with center of protractor face removed |
 | Figure 4. (A) Polarizing lens glued to bottom of PVC body; (B) Polarizing lens glued to top piece of PVC; (C) Pointer glued into the PVC body at a reading of 0° on the protractor |
 | Figure 5. Complete assembly of final polarimeter |
Note that while Figure 1 suggests that the second polarizer is rotated in order to maximize the amount of light being observed, in practice it is easier to locate the point ominimum light transmittance (i.e., when the lens goes dark). Thus, rather than initially aligning the two lenses so that they are colinear (and maximal light is transmitted) they areinstead initially aligned perpendicularly. When taking measurements, therefore, the top ring is rotated to find the point of minimum light transmittance.
4. Operation of the Polarimeter
When demonstrating the use of a polarimeter in class, the entire unit is placed on a light source (such as the base of a document camera or overhead projector) initially without the top polarizing lens or sample cell in place. The image is cast onto a suitable screen in the room. Students can readily see that the intensity of the light coming through the bottom polarizing lens is dimmed relative to the light not flowing through the lens. The top polarizing lens is then put in place and it is demonstrated that when the lens is in the 0° position, no polarized light is transmitted through the top lens, but if it is turned to 90°, all of the light is transmitted (Figure 6). | Figure 6. Images viewing through the top of the polarimeter which is sitting on a light source. (A) Obvious absence of light transmittance when the dial indicator on the top polarimeter is set to 0° (i.e., the two linear polarizers are orthogonal); (B) Complete transmittance of light when the dial indicator on the top polarimeter is set to 90° (i.e., the two linear polarizers are collinear) |
Next the beaker “sample cell” with water is placed in the polarimeter and it is demonstrated that the polarimeter acts just as if the cell were empty. No rotation of the plane of polarized light is expected (or observed) because water is achiral (Figure 7). | Figure 7. Images similar to those in Figure 5 except the sample cell was filled with water |
The sample cell is removed, the water emptied and cell dried, and then the cell is filled to ~80-90% of capacity with the compound to be analyzed. In Figure 8A is pictured the initial result when the cell is filled with (+)-α-pinene. With the top lens still at 0°, light is still transmitted through the top lens. The top lens is then rotated slowly until a minimum of transmitted light is observed (Figure 8B). For this compound, the lens must be rotated towards the right (i.e., dextrorotatory or + direction). A reading for the observed rotation is then taken from the protractor (in this case, 25°). The sample cell is then removed from the 25°). This entire measurement process may be clearly observed by students in the classroom. The sample cell is then removed from the polarimeter body and the height of the sample in the beaker (taking into account the thickness of the bottom of the beaker) is measured using a suitable ruler (in this case, 5.6 cm). Using the known density of (+)-α-pinene (d = 0.858 g/mL) the approximate specific rotation may be calculated using equation 1. Our measurements led to a value of +51° for (+)-α-pinene. The value provided by the supplier was +47° suggesting a 9% error in our value. However, given the low cost associated with the polarizers, sample cell, etc., and the fact that the light source is non-standard and the temperature not necessarily uniform, this is a reasonable error. At any rate, the procedure by which this data is obtained becomes very obvious to the students viewing in the classroom. | Figure 8. Behavior of the polarimeter when the sample cell was filled with (+)-α-pinene. (A) When the indicator dial is left at a setting of 0°, obvious light transmittance through the top polarizer lens is observed. (B) Rotating the top polarizer lens to a setting of 25° minimizes the transmission of light and this value is taken as the observed rotation |
We typically also conduct a second run using (–)-β -pinene in the sample cell to demonstrate the difference between dextrorotarory and levorotatory rotations. In this case the top polarizer must be rotated to the left (i.e., levorotatory or – direction) to observe minimum light transmittance. A sample height of 6.5 cm of liquid afforded a rotation of –14°. Using the literature density (d = 0.871 g/mL) we calculated a specific rotation of –25° (value provided by the supplier was –22°).
5. Conclusions
An inexpensive, homemade polarimeter has been developed that provides an excellent means by which to illustrate the use of a polarimeter to measure specific rotations. (+)-α-pinene and (–)-β-pinene areconvenient compounds for analysis since they are of relative low cost and have pleasant odors (of course, all compounds should be handled in a safe manner!). Furthermore, they demonstrate the observation of levorotatory versus dextrorotatory rotations. Because of the rudimentary nature of the polarimeter, values obtained have a percent error on the order of 10%. Therefore, while not suitable for quantitative experimentation, use of this unit in classroom demonstrations clearly shows students in a lecture room setting the general manner by which optical rotation data are obtained.
References
| [1] | (a) Lisboa, P.; Sotomayor, J.; Ribeiro, P. J. Chem. Ed. 2010, 87, 1408.(b) Stary, F. E.; Woldow, N. J. Chem. Ed.2001, 78, 644. (c) Isaacs, N. S. J. Chem. Ed.1983, 60, 607. (d) Meloan, C. E. J. Chem. Ed.1978, 55, 319. (e) Shavitz, R. J. Chem. Ed.1978, 55, 682. (f) Vennos, M. S. J. Chem. Ed.1969, 46, 459. (g) Gibas, M. A. J. Chem. Ed.1976, 53, 462. (h) Kapauan, A. F. J. Chem. Ed.1973, 50, 376. (i) Shaw, W. H. R. J. Chem. Ed.1955, 32, 10. (j) Nechamkin, H. J. Chem. Ed.1954, 31, 579. (k) Kiplinger, C. C. J. Chem. Ed.1930, 7, 2174. |
| [2] | (a) Mehta, A.; Greenbowe, T. J. J. Chem. Ed.2011, 88, 1194. (b) Levine, S. G.; Miller, J. J. Chem. Ed.1990, 67, 1064. (c) Silversmith, E. F. J. Chem. Ed.1988, 65, 70. (d) Dorn, H. C.; Bell, H.; Birkett, T. J. Chem. Ed.1984, 61, 1106. (e) Frank, F. J.; Kidwell, S. M. J. Chem. Ed.1969, 46, 58. (d) Henderson, G. L. J. Chem. Ed.1967, 44, 765. (e) Gavin, J. E. J. Chem. Ed.1960, 37, 515. (f) Spear, C. S. J. Chem. Ed.1960, 37, 203. (g) Noller, C. R. J. Chem. Ed.1949, 26, 269. (h) Burkett, H. J. Chem. Ed.1949, 26, 273. (i) See also, Science Buddies Staff. "Study Chirality with a Homemade Polarimeter" Science Buddies. Science Buddies, 10 Oct. 2014. Web. 9 Jan. 2015 <http://www.sciencebuddies.org/science-fair-projects/project_ideas/Chem_p073.shtml> |
| [3] | (a) 100 mL beaker was purchased from Cole Parmer (item # EW-34515-30, $4.25). (b) PVC from any home supply store. (c) Linear polarized film was purchased from Aflash Photonics (www.polarization.com, item # PF006, $15 per foot). (d) The protractor face was scaled to size on the website (radius = 2”) and printed fromhttp://www.blocklayer.com/protractor-printeng.aspx |
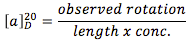






 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
