-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Laboratory Chemical Education
2014; 2(2): 11-14
doi:10.5923/j.jlce.20140202.01
Magnetic Susceptibility of Coordination Compounds in the General Chemistry Laboratory
Lauren McMills, Frazier Nyasulu, Rebecca Barlag
Department of Chemistry and Biochemistry, Ohio University, Athens, OH 45701
Correspondence to: Lauren McMills, Department of Chemistry and Biochemistry, Ohio University, Athens, OH 45701.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A general chemistry laboratory exercise is described in which the number of unpaired electrons in coordination compounds is determined. The compounds are Na2PdCl4, K4Fe(CN)6, Cr(acac)3, Na3FeF6, Co(acac)3 and Mn(acac)2. These compounds are presented to students as Na2PdA4, K4FeA6, CrB3, Na3FeA6, CoB3 and MnB2 respectively where A is monodentate, B is bidentate and both ligands have a charge of 1. For a coordination number of six an octahedral structure is assumed, and for a coordination number of four, tetrahedral and square planar structures are assumed. After determining the number of d-level electrons, students select applicable energy level diagrams and assign electrons in all possible arrangements consistent with Hund’s rule. Students cross out inappropriate diagrams, providing an explanation for why they have done so. By comparing the number of unpaired electrons determined using magnetic susceptibility and with the remaining diagrams, students deduce the structure and spin arrangement(s) that fit the experimental results. In about half of the cases, the structure is conclusively determined.
Keywords: Magnetic susceptibility, Coordination compounds, First year, Undergraduate, General chemistry
Cite this paper: Lauren McMills, Frazier Nyasulu, Rebecca Barlag, Magnetic Susceptibility of Coordination Compounds in the General Chemistry Laboratory, Journal of Laboratory Chemical Education, Vol. 2 No. 2, 2014, pp. 11-14. doi: 10.5923/j.jlce.20140202.01.
1. Introduction
- Although the pedagogical value of magnetic susceptibility measurements is well known, the cost of commercial magnetic susceptibility instruments limits their use. Some forgo commercial instruments and make their own instruments. [1-9] Recent publications usually describe simple inexpensive ways to build magnetic susceptibility instruments and results are presented mostly to show that the instrument works. Institutions that have commercial magnetic susceptibility instruments primarily use them in inorganic [10] and physical chemistry [11] where the numbers of students are typically low, so a limited number of instruments suffice. These instruments, homemade or commercial, can be particularly useful in general chemistry because it is here that students first learn electron configurations of atoms, ions and simple molecules, as well as learn to predict the number of unpaired electrons in various substances. Magnetic susceptibility in general chemistry labs is rare and one of the goals of this paper is to advocate for their use. If commercial instruments are used at this level, one of the challenges is how to accommodate a large number of general chemistry students with a limited number of instruments. The Evans type MSB-1 magnetic susceptibility balances are easy to operate, robust and portable. These are very valuable attributes for an instrument handled by hundreds of students and requiring the instrument to be moved multiple times in a single day. This lab exercise focuses on coordination compounds, and is therefore appropriate after transition elements and coordination compounds have been covered in lecture. Although the measurements take a short time, the entire lab (prelab lecture, data collection, data analysis and conclusion) takes an average of three hours. This paper also describes the strategies that have been used working with one, two and three MSB-1 magnetic susceptibility balances while serving ~600 students. This lab can also be performed using any equipment (homemade or otherwise) that can be used to determine the number of unpaired electrons in coordination compounds.In this exercise, the compound or complex ion is classified as a six-coordinate (octahedral structure is assumed) or four-coordinate species (tetrahedral or square planar structure is assumed) based on the number of ligands and the coordination number of the ligand. After determining the number of d-level electrons in each transition metal ion, participants select an energy level diagram applicable to the structure, and assign the d-level electrons allowing for all possible arrangements consistent with Hund’s rule. Students then consider the diagrams they have drawn and with explanation, cross out any inapplicable diagrams. For example, a low spin assignment for the tetrahedral structure would be crossed-out because in this case the crystal field splitting energy (t can be expected to be lower than the pairing energy (P). Considering the number of unpaired electrons that are determined experimentally (N), students find which of the remaining arrangements fit. The identity of the ligand is not provided to the students; ligands are labeled A or B depending on whether they are monodentate or bidentate and both have charges of 1. Information provided to students also includes the molar mass and counter ion molar magnetic susceptibility (XM) correction values, see Table 1. On the day of the lab, students first attend an hour long pre-lab lecture in which the theory and the operation of the magnetic susceptibility balance are described. These are described in the Supplementary Information. Samples are pre-packed for the students because: (i) At a cost of $20, sample tubes are expensive. (ii) Sample loading requires tapping of loaded sample tubes on a hard surface until the magnetic susceptibility reading becomes constant. Sample tubes are fragile therefore many would be broken. (iii) It is hard to empty a tube that has been previously loaded meaning that new tubes would need to be used each time.
2. Theory
- The theory and operation of MSB-1 magnetic susceptibility balances have been described in a number of publications. [9,10] The MSB-1 balance reports a value of R. The molar magnetic susceptibility (XM) is calculated according to the formula:
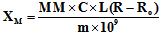 | (1) |
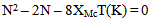 | (2) |
3. Experimental
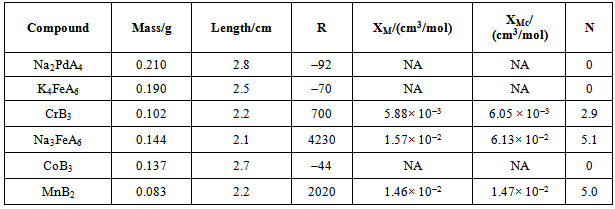
- Materials and equipmentMagnetic susceptibility balance (e.g. Mark I MSB, Johnson Matthey), sample tubes, cm ruler, thermometer, Na2PdCl4, K4Fe(CN)6, Cr(acac)3, Na3FeF6, Co(acac)3, Mn(acac)2. For students, these are labeled as indicated in Table 1.
|
- Magnetic susceptibility measurementsSamples are pre-packed for student use. Students record the sample identity, the mass of sample in the sample tube, measure the length of the sample in cm and record the value of R as reported by the balance. The value of R with an empty tube (Ro) is also recorded along with the room temperature; the sample temperature is assumed to be equal to the room temperature. Managing the number of students with a limited number of balancesOne or two balances: The balances are placed outside the stockroom from 8:30 AM to 5:00 PM for one week, allowing students to make the measurements at times convenient for them. Three balances: Measurements are made during the regular lab time with one balance in each of three laboratory rooms. Students from two sections (24 students each) take turns making the measurements. Hazards: There are no unusual hazards. Samples are sealed to prevent spillage and none require special cleanup if they are broken.
4. Results and Discussion
- The results obtained by a typical student are summarized in Table 2. Typical results on a given instrument differ by less than 3%.Na2PdA4: Pd is +2 and therefore 4d8. With a coordination number of four, the structure possibilities are tetrahedral and square planar. Considering the tetrahedral energy diagrams, the high and low spin arrangements both give 2 unpaired electrons. The low spin option is crossed out because Δt < P. Considering the square planar case, the high spin gives 2 unpaired electrons while the low spin option gives 0 unpaired electrons. The high spin option is crossed out because Δsp > P. The remaining options are tetrahedral with high spin (N = 2) and square planar (N = 0). The experimental value is N = 0. Therefore [PdA4]2 is square planar and low spin.K4FeA6 : Fe is +2 and therefore 3d6. With a coordination number of 6, the structure is octahedral. The high spin (weak-field) option yields N = 4 while the low spin (strong-field) option predicts N = 0. Since the experimentally determined value of N is 0, [Fe(A)6]4 is octahedral low spin.CrB3: Cr is +3 and therefore 3d3. With a coordination number of 6, it is octahedral. High spin and low spin configurations are identical with N = 3. The experimental value of N is 3. The classification of high spin or low spin is not designated or is not applicable.Na3FeA6: Fe is +3 and therefore 3d5. With a coordination number of 6, the structure is octahedral. The high spin case predicts N = 5 while the low spin case predicts N = 1. Since it is determined that N = 5, [FeA6]3 is octahedral high spin.CoB3: Co is +3 and therefore 3d6. With a coordination number of 6, the structure is octahedral. The high spin predicts N = 4 while the low spin case predicts N = 0. Since it is determined that N = 0, CoB3 is octahedral low spin. MnB2: Mn is +2 and 3d5. With a coordination number of four, the structure possibilities are tetrahedral and square planar. The tetrahedral high spin and low spin diagrams yield N = 5 and N = 1 respectively. The square planar high spin and low spin yield N = 5 and N = 3 respectively. The guidelines exclude the tetrahedral low spin assignment with N = 1. The guidelines also exclude the square planar high spin with N = 5 and the low spin with N = 3. That leaves the tetrahedral high spin with N = 5. Since it is determined that N = 5, MnB2 is tetrahedral and high spin.
|
5. Conclusions
- The measurements are easy and straightforward. With sample tubes packed and sealed, there is little danger in allowing unsupervised measurements, and the same samples can be used for many years. Given that balances are expensive (~$8,500 in 2012), measurements outside of lab time accommodate hundreds of students with a limited number of balances. While the initial amount of money to purchase the magnetic susceptibility balances is high, the investment can be worthwhile because the balances last a long time and require little maintenance. This exercise can also be performed using any instrumentation, homemade or otherwise. In addition to the exercise described herein, we use the magnetic susceptibility balances in two earlier laboratory exercises. The first is the determination of the number of unpaired electrons in MnO2, CuSO4•5H2O, MnSO4•H2O, KMnO4 and Fe(NH4)2(SO4)2•6H2O. This lab is performed in the 9th week of the semester, along with a hydrogen emission spectrum exercise. [12] These lab exercises are a good fit after covering quantum theory and atomic structure. The second is the determination of the number of unpaired electrons in KO2 and Na2O2. This lab is performed in the 12th week of the first semester, along with a lab on chemical models. These lab exercises are completed after models of chemical bonding and shapes of molecules have been taught in lecture. With three laboratory exercises and six years of use, the cost per student per lab is now about $0.41.In this laboratory exercise, students work with coordination compounds and in the process review many of the important terms in coordination chemistry. These include: identification of the coordination complex, structure (octahedral, tetrahedral, or square planar), ligands (monodentate or bidentate), coordination number, electron configurations of the transition metal ions, energy level diagrams, spin arrangements and number of unpaired electrons. The idea that magnetic susceptibility measurements can in some cases lead to a conclusive structure is new in the general chemistry laboratory.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML