1. Introduction

For Nash equilibria of finite player games the notion of perfect equilibria has been invented by R. Selten (1975) and by R. Myerson (1978) it has been developed as proper equilibria. Game theorists started working with refinement problems still in 1960’s [Wu Wen-Tsun and Jian Jia-He (1962)]. But for many of them keeping busy with various kinds of refinement problems has become stylish only since 1970’s. Then those have been relating to refinements of Nash equilibria. The important ones among refinements of Nash equilibrium concept are perfect equilibrium of Selten (1975), proper equilibrium of Myerson (1978), persistent equilibrium of Kalai and Samet (1984) and stable equilibrium of Kohlberg and Mertens (1986).

As far as new is theory of prenucleolies itself, so it is the first attempt of refining them for fuzzy games. We conduct analysis in formulation that is similar to the one in Schmeidler (1973).

The set of coalitions of fuzzy games that we deal with is atomless measure space. Each fuzzy coalition chooses a pure (classical) coalition from finite set of all pure coalitions. The payoff to a fuzzy coalition defines by excess of the chosen pure coalition and the average excess of the rest of coalitions. A game is a continuous mapping, which to fuzzy coalition associates a utility function.

Section 2 devoted to definitions and preliminaries of notions, which used further.

In Section 3 introduced ε-perfect (ε-proper) and as well perfect (proper) refiners. They accompanied with necessary interpretations.

That for fuzzy prenucleolies there are ε-, and full refiners we prove in Section 4.

Section 5 contains the proof of continuity for game to prenucleolies mapping.

2. Some Definitions and Notions

The definitions of fuzzy prenucleolies of a game are contained in Y. Maroutian [2024a.b]. For refinement purposes we need to redefine the fuzzy games. In the formulation that follows, fuzzy game is a pair (T, v), where 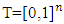is the set of all fuzzy coalitions endowed with Lebesgue measure. N is the set of all players and 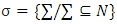is the set of pure coalitions. The pair 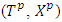refers to prenucleolies that obtained at some step p of minimization of fuzzy excesses.

An excess profile is a continuous function f from 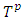to 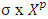, which to 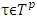maps a pair that consists of a pure coalition 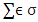and a payoff vector vector 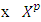. By them one can figure out excess 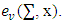By F we will denote the set of all excess profiles f. Magnitude of refers to the average excess of all coalitions from , where 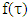replaces the excess of 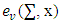that we mentioned above. For any 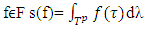and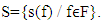

In the description below regarding to finding of the best payoffs we should stress that it is a process, which entirely based on pure coalitions.

Mapping

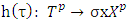for what 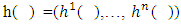is a vector function of payoff, chooses vectors 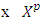for pure coalition 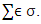Reasons that we use pure coalition from set to find best payoffs are following: 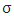is a finite set and also there are pure coalitions in set 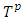too. This is something that simplifies the assessment of payoffs. Farther a game maps utility function to the pair of pure coalitions excess and average payoff of the rest of coalitions. Utility functions enable games to separate best payoffs for fuzzy coalitions. They assess the utilities of pairs 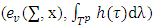. This process results to finding of the best payoff for a fuzzy coalition.

The process that we mentioned right now consists of two components by what one can model how the excess profile works. The first one of them is the rejection by coalitions of those vectors 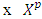that do not provide maximum payoff for, and the second component is the refinement of set 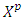of vectors with insufficient payoffs.

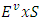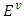Let U denote the set of real valued continuous functions called utility functions that defined on where is the set of excesses of pure coalitions 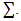We assume that U endowed with supnorm topology. Game defines as a continuous function v:T→U. Based on what’s above a fuzzy coalition’s payoff is continuous function of the pure coalition’s excess and average excess of the rest of coalitions from the set .

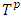The expression 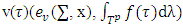calls normal form of fuzzy game (T, v).

Through it defines the magnitude of payoff for coalition

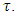“For non-cooperative games in many real, game like situations a mixed strategy has no meaning” (D. Schmeidler (1973)). We cannot share this point of view when it comes to fuzzy coalitions and from there as well to fuzzy prenucleolies in cooperative games. That is the reason because of what proving existence of a pure refinement in fuzzy cooperative game is not as important as it is doing the same for pure T-strategy equilibrium in non-cooperative games. From there we will just get along with proving the existence of arbitrary (pure or fuzzy) refiners of prenucleolies. At the same time though proving existence of pure refinement still can be counted as a problem, however here we do not keep busy with it.

3. Perfect and Proper Refiners

In this section we define perfect and proper refiners for fuzzy prenucleolies as well make some interpretations. Let F again is the set of a all continuous functions f such that 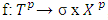, and by 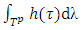we denote the average excess of all coalitions 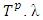is Lebesgue measure defined on T.

Definition 3.1. An ε-perfect refiner of v is a function 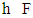such that for almost all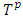

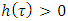and for arbitrary i,j if

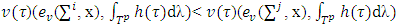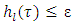then for all

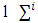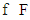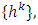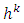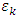Definition 3.2. A perfect refiner of v is a function if there exists a sequence where each is a -perfect refiner, 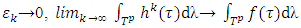and for almost all 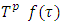limsup .

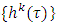Definition 3.3. An ε-proper refiner of v is a function 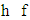such that for almost all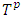

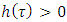and for i,j if

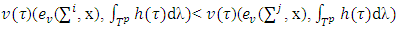then 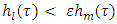for each 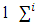and .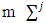

Definition 3.4. A proper refiner of v is a function 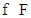if there exists a sequenc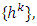e whe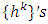re are 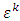-proper refiners, 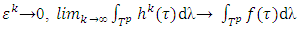and for almost all 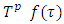limsup .

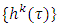Let farther describe the way refiners of the set of prenucleolies work. In definitions above to an ε-perfect (proper) refiner given infinitesimal weight if it does not provide coalition 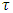with the best payoff in condition that the average payoff to the rest of coalitions remains the same. That results to refining 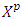from the vector 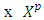, which ascribed to pure coalition 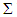by the excess profile of 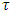. So, the written right now as well explains the essence of refiners.

The refinements we consider based on the concepts of perfectness and mistake for perturbed games. According to the concept of perfectness players with small probability make mistakes which results to forming of coalitions with pure participation of some players. This idea mathematically modeled via perturbed game, i.e a game in which players only allowed to participate in completely fuzzy coalitions.

Let (T,v) is a game and 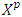is its prenucleoli. If coalition 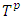and for another coalition 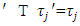when j≠k, 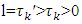also 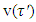has a value s.t for 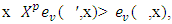then x, which is a best payoff for is not so for 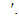From there, this is a case when full participation by a player in a coalition is not preferred. At the same time in a game (T,v) its prenucleoli 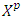not stable against the mentioned kind of perturbation in the data of the game.

4. The Existence of Refiners of Prenucleolies

We base the proof on a result of Abian S and Brown A.B (1961). That makes it much more direct and simple compared with the use of Kakutani’s theorem.

Definition. Let F: X→Y be a multifunction on X into Y. A selection for F is a single valued function f: X→Y such that 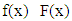for each 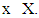An isotone (continuous, etc.) selection is a selection, which is isotone (continuous, etc.)

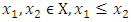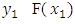Theorem 1.7. (Smithson R.E. (1971)). Let X be a partially ordered set and F:X→X be a multifunction on X satisfying the following monotonicity condition: If, and then there is 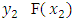such that 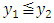. If 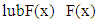for all 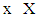then there is isotone selection for F.

Another result to be used is Theorem 3 from Abian S. and Brown A.B (1961).

Theorem 3. Let X be a partially ordered set in which every nonempty well ordered set has a lub in X. F: X→X is a multifunction on X such that for each 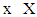there exists a 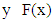satisfying to 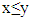. Then F has a fixed point.

Farther we will prove the existence of proper refiners.

Theorem 4.1 Exists a proper refiner in every fuzzy game that possesses with prenucleolies.

Proof. In Lemma 4.1 below we show that there is an ε-proper refiner for any 0<ε<1. Then we prove existence of proper refiners.

Lets recall again that F is the set of all continuous functions. 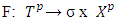, and S= 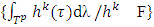is a nonempty set.

Define correspondence

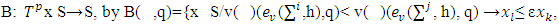for arbitrary 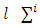and

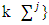Let 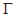be a correspondence such that and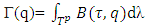

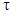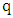Lemma 4.1 For any and sets 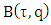and 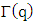are nonemtpy.

Let 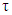and are some fixed values and 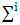is a pure coalition. Assume

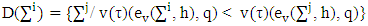and 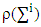is the cardinality of 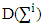denote

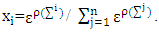From 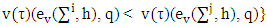follows that 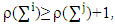of what obtains and 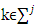. Let vector 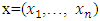with coordinates that satisfy to inequalities we just obtained is value of some function 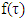at fixed coalition 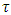. So, this way the function 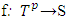. The continuity of function f follows from continuity of 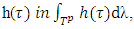in the expression of excess 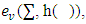joint continuity of utility function 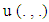from its arguments. From there really there is a continuous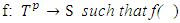 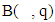for 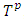, or nonemptiness of 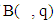has been proved.

The nonemptiness of mapping 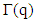for every q follows from integrability of functions f.

To apply Abian S. and Brown A.B (1961) fixed point theorem we will need that set S has been partially ordered (POS). So will be assumed that there is some relation of ordering, for example 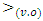vector ordering on S.

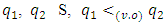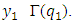Lemma 4.2. Let for and Then there is 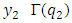such that

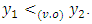Proof. By definition if 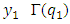then there is 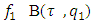such that 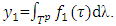To prove that for 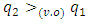there is 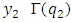for what 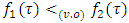for almost each 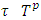one can construct function 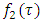by taking 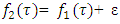for a.e. 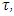where 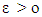is a vector s.t.

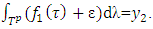Constructed this way vector 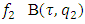and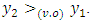

The property we just proved will be called condition of monotonicity of multifunction .

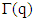Lemma 4.3. For every nonempty well ordered subset .

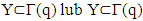Proof. Lets recall that 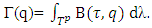For subset 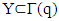one can represent lubY as limit of some sequence 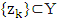where each

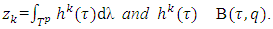From there 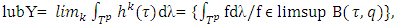where

limsup 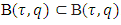. Hence, 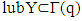for arbitrary 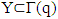and from there also for well ordered subsets of Γ(q).

Lemma 4.4 For multifunction 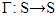if then there is such that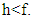

Proof. For arbitrary 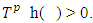From there, if to take 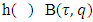the vector 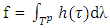will satisfy to 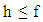inequality, which requires.

Now remains concluding the proof of theorem. In Lemmata 4.2-4.4 we have proved conditions that are in hypothesis of Theorem 3 from Abian S. and Brown A.B. (1961). Based on that mapping Γ possesses with a fixed point, which means the existence of 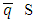such that 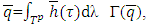and 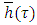is an ε-proper refiner.

Let 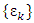be a sequence such that 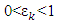and 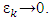Based on Lemma 4.1 for every 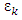there exists 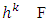such that 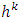is an ε-proper refiner. Due to continuity of functions 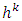that defined on close sets they are bounded and from there, so are 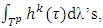and hence the sequence

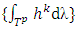contains a converging subsequence.

So, we can assume that converges 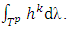That means exists

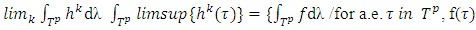is a limit point of

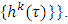By Lemma 4.1 each limit point of 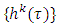belongs to

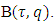The latter one proves existence of a function 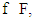which is a perfect refiner for prenucleolies of game (T,v). We concluded the proof of our theorem.

Corollary. It is obvious that existence of perfect refiners follows from the existence or proper refiners.

5. The Continuity of Game to Prenucoleolies Mappings

In this part for concave fuzzy games we prove the continuity of game to prenucleolies mappings. Let 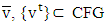and 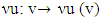is a mapping that to each game 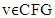corresponds the set of its prenucleolies, i.e. set .

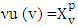Definition 5.1. A map 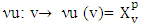is lower hemicontinuous (l.h.c.) at 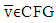if for every 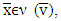if sequences 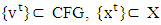are such that for each 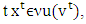when 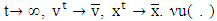is l.h.c. if it is so at every

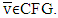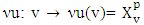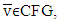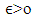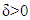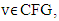
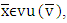
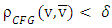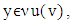
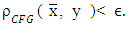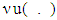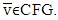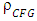Definition 5.2. A map is upper hemicontinuous (u.h.c.) at if for arbitrary exists such that when at then for all Map is upper hemicontinuous if it is so at every The and 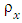are metrics on CFG and X.

Before moving ahead to ensure the continuity of map 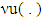we need max norm on CFG. For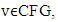

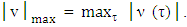Proposition 5.1. Let for 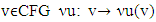is a mapping, and 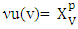is game v’s set of prenucleolies. Then mapping 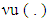is continuous.

Proof. Proving of mapping 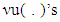continuity we start with it’s lower hemicontinuity. Let for a game 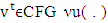is following map, i.e. 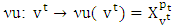. Here 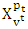is the set of prenucleolies 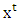for game 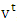, which means it is the solution of MP at last step .

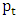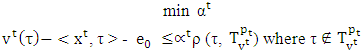(5.1)

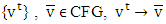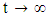Assume that when , and 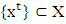is a sequence such that for every 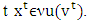Let for an 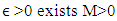a way that when

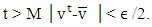Below we modify the utility function of MP(5.1)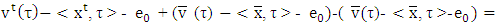

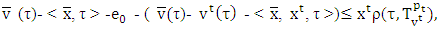Due to

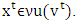From there it follows that

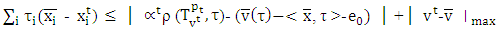When t is big enough .

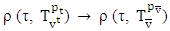Based on what we have that for an 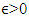, expression, which is in first module sign at right hand side of the above inequality in limit becomes:

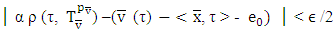in case if vector 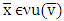. As a result we obtain that 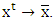The latter means the required lower hemicontinuity of mapping 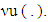To prove the upper hemicontinuity of mapping 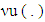at 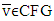lets assume that vector 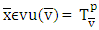. We need to show that if for 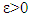there is 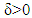such that when for some characteristic function 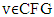takes place 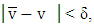then for all

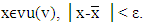Vector 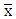is a solution for following MP:

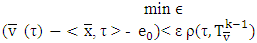where 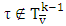and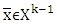

Let assume that also for some game 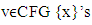are solutions of corresponding to v MP. In the following for games v and 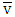we assess difference of utility functions that take part in their MP’s, i.e.

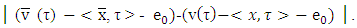From there,

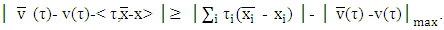For 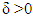small enough if 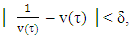then we obtain that

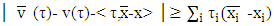(5.2)

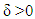For the left hand side of inequality (5.2) we need to show that if for small enough if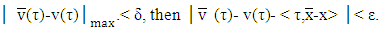

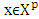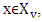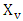As far as for every it also true that where is the set of all preimputations of 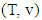, hence when 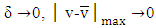and

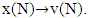From there, 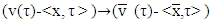For 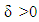small enough, i.e. in the limit case MP for game v from 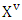transforms to MP that is for 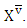It means that

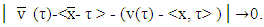The latter together with inequality (5.2) results to

for all ieN.

This is what we needed to prove.

For games 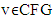possessing with single prenucleoluses the continuity of mapping 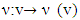remains true as well.

Proposition 5.2. For possessing with prenucleoluses games 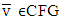mapping 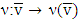is continuous.

Proof. Let 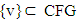are games such that for 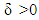small enough 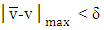and both of the games 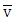and v possess with single prenucleoluses. Prenucleoluses for both kinds of games: 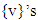and 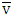are solutions of finite number of MP’s. Solutions of MP’s for 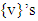when 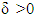is small enough because of weak inequalities that satisfy as well to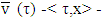 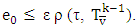By the other side, 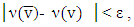because 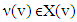and for 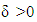small enough 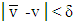as well due to fact that .

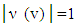This proves our propostion

Glossary and List of Notations

G=(T,v)- fuzzy game with set of coalitions T and characteristic function v. Briefly we say also game G or game v. Partially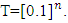

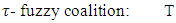
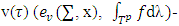normal form of a fuzzy game.

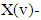set of preimputations of game v, which is a set of vectors that satisfy to condition of efficiency: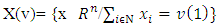

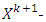inductively defined sets where k=0,1,…,p (p<∞). Each one of sets 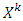corresponds to k-th step of prenucleolus’s construction: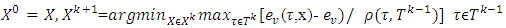

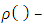metrics on set T

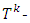set of coalitions corresponding to constructing of prenucleolies at it’s k’th step: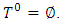

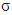-set of all pure coalitions: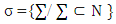

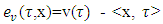excess of fuzzy coalition 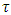from division vector x, where 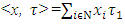is inner product of vectors x and .

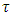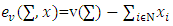excess of pure coalition 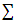from division vector x.

Function 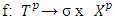continuous function called excess profile. Mapps to each fuzzy coalition 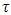a pair consiting of pure coalition 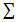and division vector x.

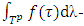average payoff of all coalitions from set 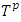, 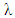is Lebesgue measure.

F- set of all excess profiles

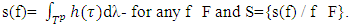U- the set of all real valued jointly continuous functions 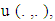defined on 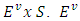is the set of excesses of pure coalitions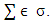

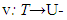continuous function. Redefinition of game for refinement purposes.

Refinement- process of separating for each coalition 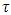it’s best payoffs from the set of all prenucleolies .

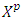Refiner- excess profile that from a coalition 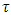receives the maximum veight based on providing with the best payoff.

Prenucleolus- unique vector to which results process of constructing of sets 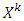after finite number of steps. Possess with prenucleolus piece-vice affine games.

Prenucleoli- set of vectors that obtain as result of stabilization of sets 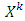started from some number 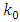. i.e for .

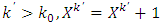MP- a minimization problem that discussed at some step m for finding of prenucleolies:

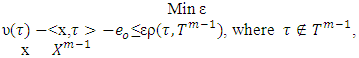CFG- the set of fuzzy concave characteristic function games.

FC- set of fuzzy coalitions.

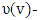the prenucleolus of game (T,v).

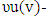the prenucleoli of game (T,v).

lubY- least upper bound of set Y

The author appreciates the reviewer and the editorial assistant for helpful comments.