-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2024; 13(3): 45-51
doi:10.5923/j.jgt.20241303.01
Received: Jun. 11, 2024; Accepted: Jul. 8, 2024; Published: Jul. 31, 2024

The Fuzzy Prenucleolus III. The Properties and Monotonic Covers
Yeremia Maroutian
1806 Miles Ave, Apt 112, Cleveland, OH 44105, USA
Correspondence to: Yeremia Maroutian, 1806 Miles Ave, Apt 112, Cleveland, OH 44105, USA.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

For possessing with prenucleolies fuzzy games we have proved that their sets of prenucleolies can be represented as super differentials. The latter one shows that these two concepts closely affiliated D. Schmiedler in classical theory proved property of super linearity for the nucleolus. We by using theory of superdifferetials the same property extended to fuzzy prenucleolies. For the fuzzy prenucleolies we as well proved property of nonmonotonicity by Megiddo. From geometric point of view, we described the way prenucleolies behave during the process of their construction. Proved that the prenucleolies invariant under operation of monotonic covering. The integration of geometric description for the construction of prenucleolies provides a novel perspective. In our view offers novel insight as well as the proof of invariance of fuzzy prenucleolies for monotonic covers of fuzzy games.
Keywords: Fuzzy prenucleolus, Fuzzy prenucleoli
Cite this paper: Yeremia Maroutian, The Fuzzy Prenucleolus III. The Properties and Monotonic Covers, Journal of Game Theory, Vol. 13 No. 3, 2024, pp. 45-51. doi: 10.5923/j.jgt.20241303.01.
Article Outline
1. Introduction
- In classical theory refer to excess based solutions the nucleolus and several other types of nucleolies. Still in nineteen forties game theorists in RAND recommended lexicographic minimization of objective functions. The recommendation published in (Brown G, 1950) and in (Dresher M., 1961).In (Schmeidler D. 1969) introduced the nucleolus of TU Games. After Schmeidler D., E. Kohlberg in (1971) has described new properties of nucleolus for TU Games. In N. Megiddo (1974) has proved nonmonotonicity of nucleolus. L. Zhu, (1991) has proved the weak coalitional monotonicity of the decision rule. Zhu’s result has been extended to fuzzy games in Y. Maroutian (2024).Section 2 describes the background and current model. Devoted to prenucleolies Section 3. As superdifferential represented sets Xk of prenucleolies. Interpreted geometrically the prenucleolus’s behavior while it is in the process of construction and described structure of sets Xk of prenucleolies.We prove the following properties for games to prenucleolies mappings ν(.), the superlinearity in section 4.1 and Section 4.2 devoted to proving of nonmonotonicity by Megiddo for prenucleolies. In section 5, we have proved that the prenucleolus remains invariant under operation of monotonic covering.
2. The Background and Current Model
2.1. Some Preliminaries on Prenucleolies
- In theory, use of the term prenucleoli has a common meaning and varies depending on type of games to what it applies. Refer to nucleolies in case of coalitional TU games the nucleolus (Schmeidler [1969], Owen [1977]) and prenucleolus (Sobolev [1975]). It has more general meaning in (Mashler et al [1992]), where nucleolies are decision rules that obtain as a result of lexicographic minimization. In (Mashler, Peleg [1977]) defined generalized nucleoli for set valued dynamic systems. Potters and Tij’s [1992] introduced matrix nucleoli and established that it is an analogue of Kohlberg’s characterization of nucleolus for TU games in terms of balanced sets (E. Kohlberg [1971]). In fuzzy theory process of prenucleolus’s finding when characteristic function of a game is not of affine type may end up with a solution, which does not possess with a unique value. This kind of decision rule we call prenucleoli of a fuzzy TU game following to classical use of that term.
2.2. Definitions and a Decision Rule
- We denote by FG and CFG the sets of all fuzzy and fuzzy concave characteristic function games respectively. FC is the sets of all fuzzy coalitions:
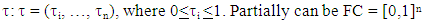 For a fuzzy game (T, ν), where
For a fuzzy game (T, ν), where 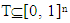 is the game’s set of fuzzy coalitions, assume
is the game’s set of fuzzy coalitions, assume 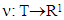 is it’s characteristic function. Set of preimputations is a set of vectors that satisfy to condition of efficiency:
is it’s characteristic function. Set of preimputations is a set of vectors that satisfy to condition of efficiency: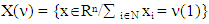 For k=0, 1, … ,p inductively defined sets Xk, where it is assumed that
For k=0, 1, … ,p inductively defined sets Xk, where it is assumed that 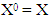 and
and 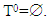 The Xk+1 are following sets:
The Xk+1 are following sets: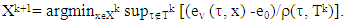 For k = 1, …, p sets Tk are as below:
For k = 1, …, p sets Tk are as below: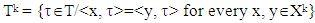
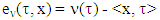 is excess of coalition
is excess of coalition 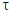 from division vector
from division vector 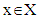 and
and 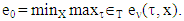 With
With 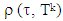 we denote distance between
we denote distance between 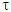 and set Tk
and set Tk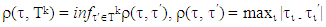 If started from some number k0, for k > k0, Tk+1 = Tk, then that in its turn entails the stabilization of corresponding set Xk or otherwise with increase of k sets Xk do not decrease anymore. That kind of stabilization of sets Xk after finite number of minimization steps may happen in case of games with no piece-wice affine characteristic functions.We call vectors from sets Xk mentioned above prenucleolies in different of unique vectors that are prenucleoluses.
If started from some number k0, for k > k0, Tk+1 = Tk, then that in its turn entails the stabilization of corresponding set Xk or otherwise with increase of k sets Xk do not decrease anymore. That kind of stabilization of sets Xk after finite number of minimization steps may happen in case of games with no piece-wice affine characteristic functions.We call vectors from sets Xk mentioned above prenucleolies in different of unique vectors that are prenucleoluses.3. The Prenucleolies
3.1. The Prenucleolies as Superdifferentials and Their Structure
- Definitions ([13]). A vector
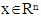 is a supergradient of concave function
is a supergradient of concave function 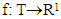 at a point
at a point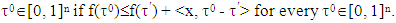 The set of supergradients of f at
The set of supergradients of f at 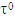 is the superdifferential of f at
is the superdifferential of f at 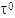 . We accept farther v∈CFG. Below we prove that for a piece-vice affine characteristic function v if v
. We accept farther v∈CFG. Below we prove that for a piece-vice affine characteristic function v if v 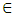 CFG, at each one of minimization steps set
CFG, at each one of minimization steps set 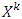 of solutions
of solutions 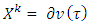 where
where 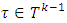 . The proof based on the fact that when k increases sets
. The proof based on the fact that when k increases sets 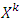 decrease monotonic, i.e.
decrease monotonic, i.e. 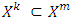 , if k>m.Let us now consider MP discussed at some step m for finding of prenucleolies, i.e.
, if k>m.Let us now consider MP discussed at some step m for finding of prenucleolies, i.e.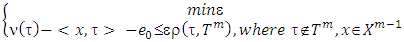 If at the same time consider MP, which is at step k, for k>m, then because sets {X𝑙} decrease with 𝑙 increasing, so we will have that there is x∈Xm such that it belongs also to Xk and that way satisfies to MP of step k:
If at the same time consider MP, which is at step k, for k>m, then because sets {X𝑙} decrease with 𝑙 increasing, so we will have that there is x∈Xm such that it belongs also to Xk and that way satisfies to MP of step k: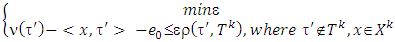 As far as k>m and in each one of the following to m steps of minimization magnitudes of excesses for coalitions
As far as k>m and in each one of the following to m steps of minimization magnitudes of excesses for coalitions 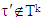 decrease compared with the ones that have been at step m, hence
decrease compared with the ones that have been at step m, hence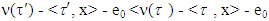 from where
from where 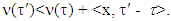 The last inequality means that each
The last inequality means that each 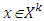 is a supergradient of characteristic function
is a supergradient of characteristic function 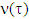 from game (T, ν) at
from game (T, ν) at 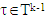 or
or 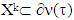 . The opposite inclusion, i.e.
. The opposite inclusion, i.e. 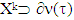 one can obtain by taking a vector
one can obtain by taking a vector 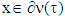 . The latter one, i.e that really there is
. The latter one, i.e that really there is 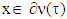 , and hence, that
, and hence, that 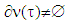 one can claim based on concavity of
one can claim based on concavity of 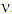 . We will come to already obtained inclusion’s opposite one by reversing the proof above. That results in the following:Proposition 3.1.1. For a piece-wice affine concave characteristic function
. We will come to already obtained inclusion’s opposite one by reversing the proof above. That results in the following:Proposition 3.1.1. For a piece-wice affine concave characteristic function 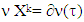 , where
, where 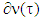 , is superdifferential of
, is superdifferential of 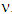 at
at 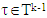 .Remark. Set of concave functions intersects with the set of piece-wice affine characteristic functions. While proving proposition 3.1.1 as by product we have obtained no emptiness of sets Xk. Theory of superdifferentials is a convenient tool for assessing sets Xk and researching through them prenucleolies of concave characteristic function games. Below we prove another presentation for sets Xk.Proposition 3.1.2.
.Remark. Set of concave functions intersects with the set of piece-wice affine characteristic functions. While proving proposition 3.1.1 as by product we have obtained no emptiness of sets Xk. Theory of superdifferentials is a convenient tool for assessing sets Xk and researching through them prenucleolies of concave characteristic function games. Below we prove another presentation for sets Xk.Proposition 3.1.2. 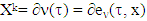 for a concave ν and
for a concave ν and 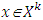 . Proof. We need to show only that
. Proof. We need to show only that 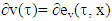 . First lets prove that
. First lets prove that 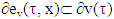 . Because ν∈CFG then by τ concave is also
. Because ν∈CFG then by τ concave is also 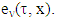 Hence,
Hence, 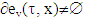 and there is
and there is 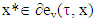 for
for 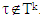 . Then for a coalition
. Then for a coalition 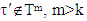
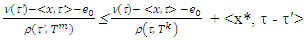 Because
Because 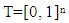 so for
so for 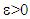 there is
there is 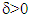 such that
such that 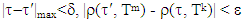 and then for ε small enough we will have that
and then for ε small enough we will have that 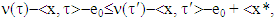
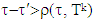 from where,
from where, 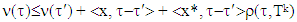 as far as
as far as 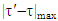 can be arbitrarily small, hence can be so as well
can be arbitrarily small, hence can be so as well 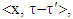 which means that
which means that 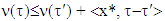 i.e.
i.e. 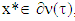 , and from there
, and from there 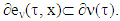 The other inclusion
The other inclusion 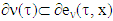 one can obtain by repeating the same arguments in reverse order.The proved right now together with Proposition 3.1.1. concludes the proof of our statement. Proposition 3.1.3. Let
one can obtain by repeating the same arguments in reverse order.The proved right now together with Proposition 3.1.1. concludes the proof of our statement. Proposition 3.1.3. Let 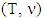 be a fuzzy game, where ν is a piece-wice affine, concave characteristic function such that
be a fuzzy game, where ν is a piece-wice affine, concave characteristic function such that 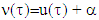 and
and 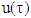 is a linear function. Then for
is a linear function. Then for 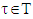 exists
exists 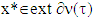 satisfying to
satisfying to 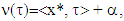 where ext
where ext 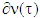 is the set of extreme points of
is the set of extreme points of 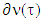 .Proof. Let v is a concave piece-wice affine characteristic function,
.Proof. Let v is a concave piece-wice affine characteristic function,  it’s superdiffrential at some point τ∈T and
it’s superdiffrential at some point τ∈T and 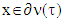 is an arbitrary vector.Below we will prove that for games possessing with either prenucleolus or prenucleoli and for vector
is an arbitrary vector.Below we will prove that for games possessing with either prenucleolus or prenucleoli and for vector 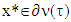 holds true equality
holds true equality 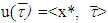 in case if
in case if 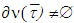 . We assume that ν∈CFG,
. We assume that ν∈CFG, 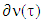 and
and 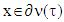 as they are above. Then
as they are above. Then 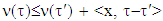 for arbitrary
for arbitrary 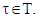 From there
From there 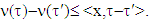 Farther, let denote by
Farther, let denote by 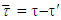 .If
.If 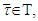 we will have that for every
we will have that for every 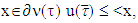
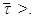 We can obtain the same inequality as well based on
We can obtain the same inequality as well based on 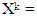
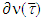 for
for  . By Proposition 3.1.2. for the games that we are dealing with
. By Proposition 3.1.2. for the games that we are dealing with 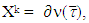 when
when 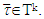 From there statement of Proposition 3.1.3. takes place if for
From there statement of Proposition 3.1.3. takes place if for 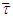 exists Tk such that
exists Tk such that 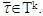 For x, y∈Xk if
For x, y∈Xk if 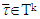 then
then 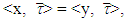 which means that
which means that 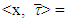 const for all
const for all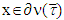 . The same remains true as well for
. The same remains true as well for 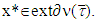 Hence, for every
Hence, for every 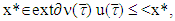
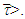 To conclude the proof let assume that for linear function
To conclude the proof let assume that for linear function 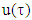 holds true only
holds true only 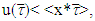 when
when 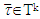 and
and 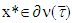 is an arbitrary vector. By the other side because
is an arbitrary vector. By the other side because 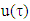 is a linear function, hence exists
is a linear function, hence exists 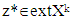 such that
such that 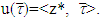 From there we are obtaining that
From there we are obtaining that 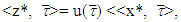 which is a contradiction. That proves our statement, i.e. exists
which is a contradiction. That proves our statement, i.e. exists 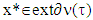 such that
such that 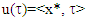 and from there in its turn also
and from there in its turn also 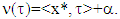 Statement 3.1.4. If
Statement 3.1.4. If 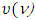 is a prenucleolus of game
is a prenucleolus of game 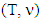 and k is a number such that
and k is a number such that 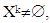 then
then 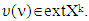 Proof. It is immediate and follows from definitions of sets Xk and extXk.Statement 3.1.5.
Proof. It is immediate and follows from definitions of sets Xk and extXk.Statement 3.1.5. 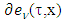 is a convex set if there is number k such that
is a convex set if there is number k such that 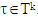 .Proof. Follows from Proposition 3.1.2. and convexity of sets Xk.Statement 3.1.6. For a game
.Proof. Follows from Proposition 3.1.2. and convexity of sets Xk.Statement 3.1.6. For a game 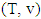 with linear characteristic function ν if
with linear characteristic function ν if 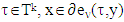 and
and 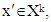 then
then 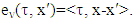 Proof.
Proof. 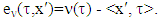 According to Proposition 3.1.3. for
According to Proposition 3.1.3. for 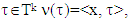 where
where 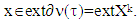 From there we have that if
From there we have that if 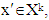 then
then 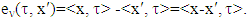 The following refers to structure of sets Xk for linear characteristic function games.Proposition ([13]). If
The following refers to structure of sets Xk for linear characteristic function games.Proposition ([13]). If 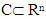 is compact convex set then C=conνh(extC). We note by conνhA the conνh of set A.This proposition can be applied to sets
is compact convex set then C=conνh(extC). We note by conνhA the conνh of set A.This proposition can be applied to sets 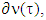 where ν is a strongly bounded game. Proposition 3.1.7. For set
where ν is a strongly bounded game. Proposition 3.1.7. For set 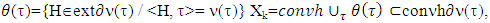 where
where 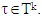 Proof. By Proposition 3.1.3., for some
Proof. By Proposition 3.1.3., for some 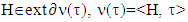 where
where 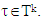 From there follows the first equation, which is above, i.e.
From there follows the first equation, which is above, i.e. 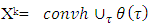 . Farther, as far as by definition
. Farther, as far as by definition 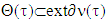 , hence
, hence 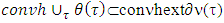 . This is what has been required. Remark. Based on Proposition ([13]) in formulation of Proposition 3.1.7 for strongly bounded games instead of inclusion sign takes place equality.
. This is what has been required. Remark. Based on Proposition ([13]) in formulation of Proposition 3.1.7 for strongly bounded games instead of inclusion sign takes place equality.3.2. A Geometric Description on the Prenucleolus’s Construction
- The way sets Xk behave during the process of prenucleolus’s constructing allows to describe it geometrically. That description based on theory of superdifferentials and refers to
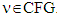 .The position of a set Xk defines by position of its supporting hyperplane. Point
.The position of a set Xk defines by position of its supporting hyperplane. Point 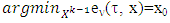 through what passes supporting hyperplane belongs to
through what passes supporting hyperplane belongs to 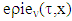 of map
of map 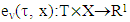 and supports
and supports 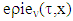 with each step of minimization. The position of supporting hyperplane changes relative to position of similar set that has been at previous step. On set
with each step of minimization. The position of supporting hyperplane changes relative to position of similar set that has been at previous step. On set 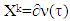 position’s changes and equivalently changes in directions of supergradients containing in
position’s changes and equivalently changes in directions of supergradients containing in 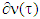 during constructing of prenucleolus one can get an idea by comparing expressions of supergradients at two consecutive steps of minimization. At the same time takes place change in position of the supporting hyperplane at each step of the prenucleolus’s construction. From there, one can say that while constructing a prenucleolus the supporting hyperplane and together with it the entire set Xk oscillate around a certain position. Sets Xk keep oscillating with each step until they reach their final position at the last step. That is when defines position of the prenucleolus. The latter one of course refers to games that possess with unique prenucleolus.Now let recall again that the present description is about the class of games that possess with superdifferentials, i.e. games with concave characteristic functions. That class intersects with piece-wice affine games. From there though not every concave characteristic function game has a prenucleolus and hence, it is not always that the described oscillations of sets Xk will come to a final state and stop, however described oscillations will take place for all those games that possess with prenucleolies.
during constructing of prenucleolus one can get an idea by comparing expressions of supergradients at two consecutive steps of minimization. At the same time takes place change in position of the supporting hyperplane at each step of the prenucleolus’s construction. From there, one can say that while constructing a prenucleolus the supporting hyperplane and together with it the entire set Xk oscillate around a certain position. Sets Xk keep oscillating with each step until they reach their final position at the last step. That is when defines position of the prenucleolus. The latter one of course refers to games that possess with unique prenucleolus.Now let recall again that the present description is about the class of games that possess with superdifferentials, i.e. games with concave characteristic functions. That class intersects with piece-wice affine games. From there though not every concave characteristic function game has a prenucleolus and hence, it is not always that the described oscillations of sets Xk will come to a final state and stop, however described oscillations will take place for all those games that possess with prenucleolies.4. Properties
4.1. The Superlinearity of Mapping vu (.)
- This part together with property of superlinearity of mapping
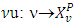 as a function of ν contains as well a result on nonmonotonicity of prenucleolies by Megiddo.This property of mapping
as a function of ν contains as well a result on nonmonotonicity of prenucleolies by Megiddo.This property of mapping 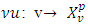 insighted from Schmeidler (1969) where it relates to nucleolus of classical characteristic function. D Schmeidler defined it in terms of lexicongraphic minimization and hence, for proving the superlinearity the methods that used there are different of ours. Proposition 4.1.1. The set of CFG of all fuzzy concave characteristic function games is a convex and closed cone. For every
insighted from Schmeidler (1969) where it relates to nucleolus of classical characteristic function. D Schmeidler defined it in terms of lexicongraphic minimization and hence, for proving the superlinearity the methods that used there are different of ours. Proposition 4.1.1. The set of CFG of all fuzzy concave characteristic function games is a convex and closed cone. For every 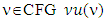 is a superlinear mapping.Proof. That CFG is a convex and closed cone proves directly. That is the reason for omitting it here. Farther, we are going to deal with sets
is a superlinear mapping.Proof. That CFG is a convex and closed cone proves directly. That is the reason for omitting it here. Farther, we are going to deal with sets 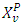 as superdifferentials
as superdifferentials 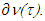 We have proved in Proposition 3.1.2 that for
We have proved in Proposition 3.1.2 that for 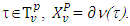 Suppose
Suppose 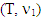 and
and 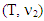 are games, where
are games, where 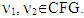 By definition of superdifferentials for
By definition of superdifferentials for 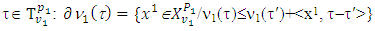 and similarly, for
and similarly, for  Also,
Also, 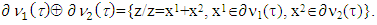 That means for
That means for 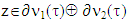 takes place:
takes place: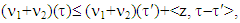 or otherwise,
or otherwise, 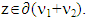 Hence,
Hence, 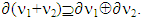 To prove the superlinearity of
To prove the superlinearity of 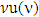 for our needs we will use relation
for our needs we will use relation 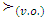 for vectors from set
for vectors from set 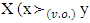 for
for 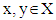 if for all
if for all 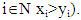 We require that for vectors
We require that for vectors 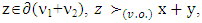 where
where 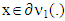 and
and 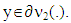 Otherwise, from there it would follow that violates condition of
Otherwise, from there it would follow that violates condition of 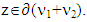 The latter one means that for arbitrary
The latter one means that for arbitrary 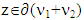 holds true inequality z≥x+y, which in its turn means that
holds true inequality z≥x+y, which in its turn means that 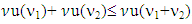 . From there we have
. From there we have 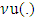 really possesses with property of superlinearlity.
really possesses with property of superlinearlity.4.2. The Nonmonotonicity of Fuzzy Prenucleolies by Megiddo
- On this property there is the work of N. Megiddo (1974) for the nucleolus of classical characteristic function games. We extend his result to fuzzy prenucleolies.Let
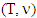 and
and 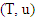 are two fuzzy TU games and
are two fuzzy TU games and 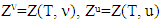 are sets of prenucleolies for games
are sets of prenucleolies for games 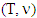 and
and 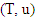 respectively. We denote by B the following collection of coalitions:
respectively. We denote by B the following collection of coalitions: 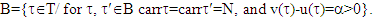 For all
For all  i.e.
i.e. 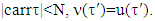 Definiton 4.2.1. We will say that prenucleolies for games
Definiton 4.2.1. We will say that prenucleolies for games 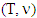 and
and 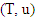 are monotonic if for
are monotonic if for 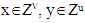 and arbitrary
and arbitrary 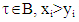 where
where  We call it monotonicity by Megiddo.Proposition 4.2.1. For fuzzy games
We call it monotonicity by Megiddo.Proposition 4.2.1. For fuzzy games 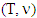 , when
, when 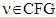 , its prenucleolies are not monotonic by Megiddo.Proof. First, it is clear that prenucleolies
, its prenucleolies are not monotonic by Megiddo.Proof. First, it is clear that prenucleolies 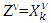 and
and 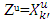 are solutions of known MP’s for games (T, ν) and (T, u) at some steps k and k′ when each one of these sets get stabilized. We have proved in Proposition 3.1.2 that
are solutions of known MP’s for games (T, ν) and (T, u) at some steps k and k′ when each one of these sets get stabilized. We have proved in Proposition 3.1.2 that 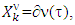
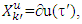 where
where 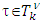 and
and 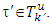 Let consider superdifferential
Let consider superdifferential 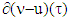 for coalitions
for coalitions 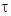 and
and 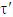 , where
, where 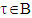 and
and 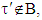 as well for vectors
as well for vectors 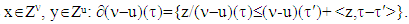 Because
Because 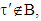 hence
hence 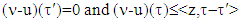 Now we are going to choose coalitions τ and τ′ the following way:
Now we are going to choose coalitions τ and τ′ the following way: 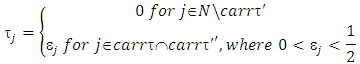 And
And 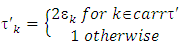 In case of chosen that way coalitions
In case of chosen that way coalitions 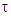 and
and 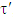 the inequality above holds true only for
the inequality above holds true only for 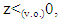 which means that
which means that 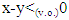 or
or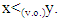 From there,
From there, 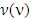 is not monotonic. The proposition proved. Remark. The nonmonotonicity of fuzzy prenucleoluses, which corresponds to the case when
is not monotonic. The proposition proved. Remark. The nonmonotonicity of fuzzy prenucleoluses, which corresponds to the case when  , follows directly from proposition we have proved.
, follows directly from proposition we have proved.5. On the Prenucleolus of Monotonic Covers
- Definition 5.1. For a piece-wice affine characteristic function fuzzy game
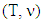 its monotonic cover is a game
its monotonic cover is a game 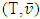 that for a coalition
that for a coalition 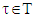 defines as:
defines as: 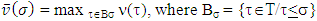 The preference relation between coalitions
The preference relation between coalitions 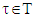 we will consider in this section in sense of vector ordering
we will consider in this section in sense of vector ordering 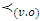 Theorem 5.1 For a fuzzy piece-wice affine characteristic function game its prenucleolus invariant under operation of monotonic covering.Proof. Let
Theorem 5.1 For a fuzzy piece-wice affine characteristic function game its prenucleolus invariant under operation of monotonic covering.Proof. Let 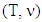 is a fuzzy game that mentioned in theorem’s formulation. Below is a minimization problem (MP) for
is a fuzzy game that mentioned in theorem’s formulation. Below is a minimization problem (MP) for 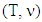 :
: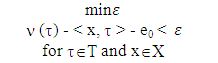
 (1)We have proved in Y. Maroutian (2017) that solution
(1)We have proved in Y. Maroutian (2017) that solution 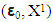 for LPP (1′) below is also solution for MP(1).
for LPP (1′) below is also solution for MP(1).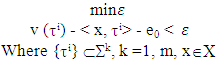
 (1')
(1')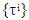 here is set of peaks of simplexes
here is set of peaks of simplexes 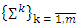 that cover the set of T. It has been proved that a game
that cover the set of T. It has been proved that a game 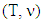 possesses with prenucleolus when minimization problems below, where
possesses with prenucleolus when minimization problems below, where 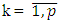 have solutions:
have solutions: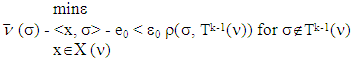 We assume that set
We assume that set 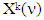 is the solution of MP above. There will be need for dealing parallelly with similar constructs that refer to either one of the games:
is the solution of MP above. There will be need for dealing parallelly with similar constructs that refer to either one of the games: 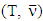 or
or  . Deserves for separate discussion the case when points of maximum of function
. Deserves for separate discussion the case when points of maximum of function 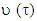 for
for 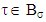 are falling out of sets
are falling out of sets 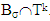 . If for
. If for 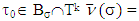
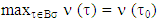 then because from
then because from 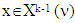 it follows that also
it follows that also 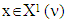 hence the left hand side of the inequality, which contains the utility function in MP for
hence the left hand side of the inequality, which contains the utility function in MP for 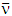 becomes negative due to equality to zero of its right hand side. From there to find points of maximum of
becomes negative due to equality to zero of its right hand side. From there to find points of maximum of 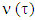 considering only set
considering only set 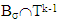 does not suffice. Hence, instead one should consider the entire set
does not suffice. Hence, instead one should consider the entire set 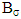 . Let
. Let 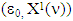 as above is the solution of MP (1) for game
as above is the solution of MP (1) for game 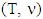 . We show first that exists solution of MP for
. We show first that exists solution of MP for 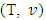 such that
such that 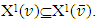 For
For 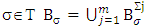 where,
where, 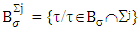 . Every set
. Every set 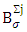 is compact. In its turn, the characteristic function ν(τ) is continuous. From there on each one of sets
is compact. In its turn, the characteristic function ν(τ) is continuous. From there on each one of sets 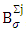 , there is
, there is 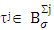 such that
such that 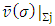 =
= 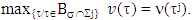 Due to the finite number of points of maximum
Due to the finite number of points of maximum 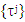 exists
exists 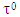 such that
such that 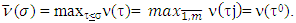 Based on that
Based on that 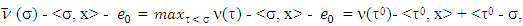
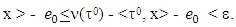 From there for
From there for 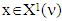 and as well for coalitions
and as well for coalitions 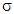 and
and 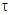 such that
such that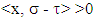 holds true
holds true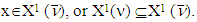 For
For 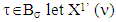 be the following set:
be the following set: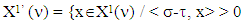 for pairs of coalitions such that
for pairs of coalitions such that 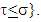 The set
The set 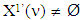 because
because 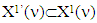 and there are coalitions
and there are coalitions 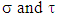 such that
such that 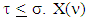 refers to the set of all preimputations of
refers to the set of all preimputations of 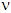 . From there, the MP:
. From there, the MP: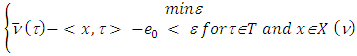 possesses with solution
possesses with solution 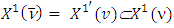 Farther we describe sets
Farther we describe sets 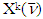 and
and 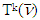 for arbitrary k through three statements.Statement 5.1. For a vector
for arbitrary k through three statements.Statement 5.1. For a vector 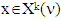 takes place also
takes place also 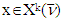 if and only if when for pairs of coalitions σ and τ0 such that
if and only if when for pairs of coalitions σ and τ0 such that 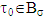 and
and 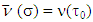 holds true
holds true 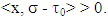 Proof. Necessity. Let
Proof. Necessity. Let 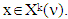 That means for solution of MP on game (T, ν), which is (ε0, Xk(ν)) holds true the following inequality:(S1)
That means for solution of MP on game (T, ν), which is (ε0, Xk(ν)) holds true the following inequality:(S1) 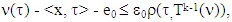 where
where 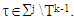 To state that the same vector
To state that the same vector 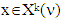 belongs as well to
belongs as well to 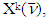 means requiring that a similar inequality took place for MP, which this time refers to game
means requiring that a similar inequality took place for MP, which this time refers to game 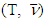 and has solution
and has solution 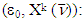 (S2)
(S2) 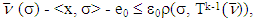 where
where 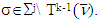 By the other side
By the other side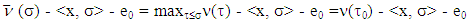
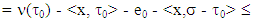 where
where 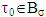 is a coalition for what
is a coalition for what 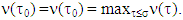 To obtain that vector
To obtain that vector 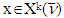 in the chain above first we should provide the condition (S1), i.e. requiring what is below:
in the chain above first we should provide the condition (S1), i.e. requiring what is below: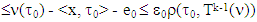 when
when 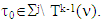 Of what we have had now first follows that really
Of what we have had now first follows that really 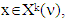 and second that it takes place, when
and second that it takes place, when 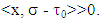 Sufficiency. Let
Sufficiency. Let 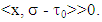 We need to prove that if
We need to prove that if 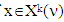 then it also belongs to
then it also belongs to 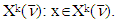 From
From 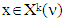 we have that for arbitrary
we have that for arbitrary 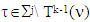
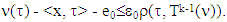
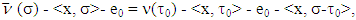 where
where 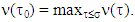 From
From 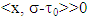 it follows that
it follows that 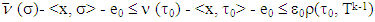 and hence,
and hence, 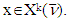 Statement 5.2. For
Statement 5.2. For 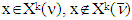 when exists a pair
when exists a pair 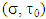 such that
such that 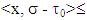
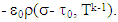 Proof. If for
Proof. If for 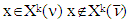 then there is a coalition
then there is a coalition 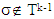 such that
such that 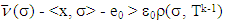
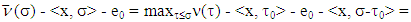
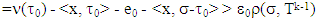 then because
then because 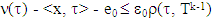 for arbitrary
for arbitrary 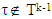 so from there,
so from there, 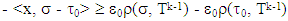
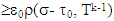 by the property of triangle for metrics.That is what required. As a result we obtain that
by the property of triangle for metrics.That is what required. As a result we obtain that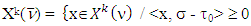 for arbitrary pair of coalitions
for arbitrary pair of coalitions 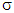 and
and 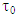 such that
such that 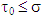 and
and 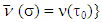 . Hence,
. Hence, 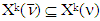 Remark 5.1. Sets
Remark 5.1. Sets 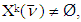 because
because 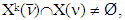 where
where 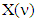 is the set of all preimputations of game
is the set of all preimputations of game 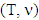 .Statement 5.3. For arbitrary
.Statement 5.3. For arbitrary 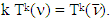 Proof. Let
Proof. Let 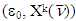 is the solution of k’th MP for game
is the solution of k’th MP for game 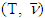 . That means we can state the following: if
. That means we can state the following: if 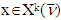 , then for arbitrary
, then for arbitrary 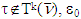 is the minimal value of
is the minimal value of 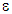 in the inequality:
in the inequality: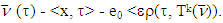 From there, because
From there, because 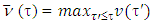 so
so 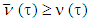 and
and 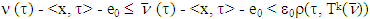 , for arbitrary
, for arbitrary 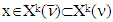 and
and 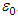 . At the same time
. At the same time 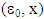 also minimizes the expression
also minimizes the expression 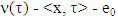 because
because 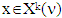 . That means
. That means 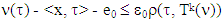 for
for 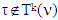 .Farther, for arbitrary
.Farther, for arbitrary 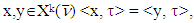 where
where 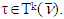 Because the same hold true for
Because the same hold true for 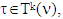 hence
hence 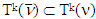 .Let’s now move ahead and prove the opposite inclusion, i.e.
.Let’s now move ahead and prove the opposite inclusion, i.e. 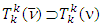 . Assume that
. Assume that 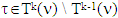 . Then for
. Then for 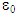 and
and 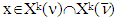 holds true the following inequality:
holds true the following inequality: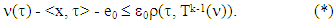 There is
There is 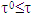 such that
such that 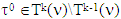 and
and 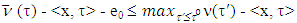
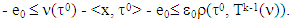 In case, when
In case, when 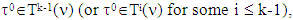 the last inequality in the above chain remains true, because then
the last inequality in the above chain remains true, because then 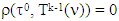 and from where it’s left side is negative. As far as
and from where it’s left side is negative. As far as  so
so 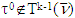 for
for 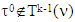 . From there,
. From there, 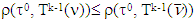 for
for 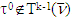 .By definition of metrics
.By definition of metrics 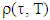 we have that if
we have that if 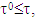 then
then 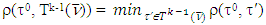
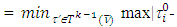
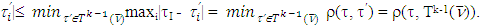 So the inequality
So the inequality 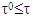 entails that
entails that 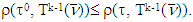 As a conclusion we will have that
As a conclusion we will have that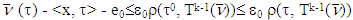 or just
or just 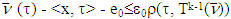 , where
, where 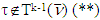 .The latter one means (ε0, x), the pair, which minimizes (**) inequality, does the same also with the inequality (*). Something that refers this time to MP for game
.The latter one means (ε0, x), the pair, which minimizes (**) inequality, does the same also with the inequality (*). Something that refers this time to MP for game 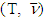 .So,
.So, 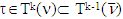 . From there,
. From there, 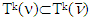 . The proved right now inclusion with the opposite one, which we have proved above provides as with one required by statement 5.3.Remark 5.2. Based on equality
. The proved right now inclusion with the opposite one, which we have proved above provides as with one required by statement 5.3.Remark 5.2. Based on equality 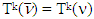 from statement 5.3. we can claim the following properties for sets
from statement 5.3. we can claim the following properties for sets 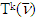 :a.) Sets
:a.) Sets 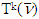 are convexb.) Sets
are convexb.) Sets 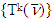 are monotonic increasing c.) With increase of k increases also
are monotonic increasing c.) With increase of k increases also 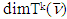 Remark 5.3. Sets
Remark 5.3. Sets  are convex. The proof of this statement is immediate. To prove increasingness of
are convex. The proof of this statement is immediate. To prove increasingness of 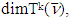 we don’t use the mentioned property of sets
we don’t use the mentioned property of sets 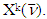 Now we are ready to conclude the theorem’s proof. As we mentioned that above the equality
Now we are ready to conclude the theorem’s proof. As we mentioned that above the equality 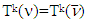 provides growth of
provides growth of 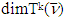 with each pair of new sets
with each pair of new sets 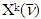 and
and 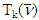 of game
of game 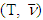 that are constructed. From there, after finite number of steps due to convexity of sets
that are constructed. From there, after finite number of steps due to convexity of sets 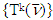 last set
last set 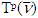 will coincide with T and the corresponding to it set
will coincide with T and the corresponding to it set 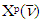 will consist of only one vector, which is prenucleolus
will consist of only one vector, which is prenucleolus 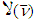 of game
of game 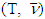 . This results to conclusion of theorem’s proof with following statement.Statement 5.4. If
. This results to conclusion of theorem’s proof with following statement.Statement 5.4. If 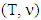 is a piece-wice affine fuzzy characteristic function game and
is a piece-wice affine fuzzy characteristic function game and 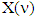 is it’s set of preimputations then the prenucleolus of monotonic cover
is it’s set of preimputations then the prenucleolus of monotonic cover 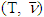 of game
of game  conincides with prenucleolus of
conincides with prenucleolus of 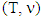 , which is
, which is 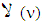 .
.ACKNOWLEDGEMENTS
- The author is very thankful to an anonymous referee, an Associate Editor and the editor of the Journal of Game Theory for their helpful comments.
Glossary and List of Notations
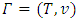 – fuzzy game with set of coalitions
– fuzzy game with set of coalitions 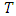 and characteristic function
and characteristic function 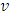 . Briefly, we say also game
. Briefly, we say also game 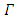 or game
or game 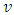 .
. 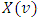 – set of preimutations of game
– set of preimutations of game 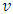 , which is a set of vectors that satisfy to condition of efficiency:
, which is a set of vectors that satisfy to condition of efficiency: 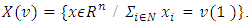
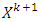 – inductively defined sets where
– inductively defined sets where 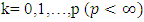 . Each one of sets
. Each one of sets 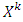 corresponds to k-th step of construction of prenucleolus:
corresponds to k-th step of construction of prenucleolus: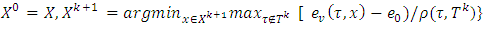
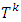 – set of coalitions corresponding to k’ th step of constructing of prenucleolies:
– set of coalitions corresponding to k’ th step of constructing of prenucleolies: 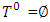
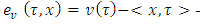 excess of coalition
excess of coalition 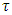 from division vector x, where
from division vector x, where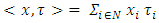 is inner product of vectors x and
is inner product of vectors x and 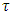 .
. 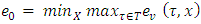 .
.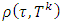 – distance between coalition
– distance between coalition 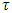 and set
and set 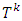 .
.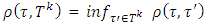 , where
, where 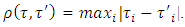 prenucleolus – unique vector to which results process of constructing of sets
prenucleolus – unique vector to which results process of constructing of sets 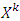 after finite number of steps. Possess with prenucleolus piece- vice affine games.Prenucleoles- set of vectors that obtain as a result of stabilization of sets
after finite number of steps. Possess with prenucleolus piece- vice affine games.Prenucleoles- set of vectors that obtain as a result of stabilization of sets 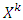 started from some number
started from some number  , i.e. for
, i.e. for 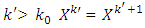 MP – a minimization problem that discussed at some step m for finding of prenucleolies.
MP – a minimization problem that discussed at some step m for finding of prenucleolies. 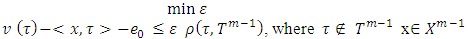 FG, CFG – sets of fuzzy and fuzzy concave characteristic function games. FC – set of all fuzzy coalitions: partially
FG, CFG – sets of fuzzy and fuzzy concave characteristic function games. FC – set of all fuzzy coalitions: partially 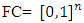
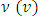 – the prenucleolus of characteristic function game (T, v).
– the prenucleolus of characteristic function game (T, v).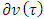 and
and 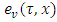 – superdifferentials respectively of game
– superdifferentials respectively of game 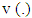 at point
at point 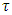 and excess
and excess 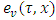 .
.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML