1. Introduction

In this paper, we pass from a simple Euclidean game to a more generalized topological game, which incorporates concepts from optimal control theory and investigate the structure of the game in the topology space. The intersection of game theory and topology structure [1] provides a fascinating lens through which to analyze strategic interactions in abstract settings. By considering strategic games within the framework of topological spaces, we can explore the intricate dynamics that emerge when strategic players navigate through nested open sets and manipulate spaces to their advantage.

Game theory is a powerful tool for studying strategic decision-making, where players aim to optimize their outcomes in a competitive environment. Topological spaces, on the other hand, offer a unique perspective on the structure and connectivity of spaces, providing a rich mathematical framework for understanding relationships and interactions.

In this study, we delve into the realm of strategic game modeling in the context of topological spaces, aiming to uncover the strategic depth and complexities that arise when game strategies are analyzed through a topological lens. By drawing parallels between game strategies and topological concepts, we seek to illuminate the strategic decisions made by players as they navigate through abstract spaces and make choices to outmaneuver their opponents.

Through this exploration, we aim to shed light on the interplay between strategic decision-making (Optimal Control Problems) [2] and topological Games, offering insights into the strategic maneuvers, optimal strategies, and outcomes that unfold in the realm of strategic games viewed through the lens of topology.

2. Problem Statement & Literature Review

The intersection of game theory and topology provides a rich framework for analyzing strategic interactions in abstract settings, yet there remains a gap in understanding the specific implications and applications of modeling strategic games within the context of topological spaces. [3] While game theory offers insights into strategic decision-making and optimal strategies, topology provides a geometric perspective on spaces and connectivity, adding a layer of complexity to strategic interactions.

The problem statement of this study revolves around exploring how strategic games can be effectively modeled and analyzed within the realm of topological spaces. By investigating the interplay between game strategies and topological structures, we aim to uncover the nuances of strategic decision-making in abstract game scenarios and understand how topological properties influence strategic outcomes.

Previous research has explored the application of game theory in various domains, ranging from economics and political science to computer science and biology. Game theory provides a formal framework for analyzing strategic interactions, equilibrium concepts, and optimal decision-making strategies. On the other hand, topology has been utilized in diverse fields such as geometry, robotics, and data analysis to study geometric properties, connectivity, and spatial relationships.

Few studies have delved into the combination of game theory and topology, particularly in the context of modeling strategic games. By incorporating topological spaces into the analysis of strategic interactions, this article has the opportunity to explore new dimensions of complexity, connectivity, and strategic maneuvering in abstract game settings.

Some existing literature has touched on related topics, such as complexity theory in games, strategic network formation, and spatial games. However, a comprehensive exploration of strategic game modeling in the context of topological spaces is still lacking. This study seeks to fill this gap by providing a detailed analysis of the implications and applications of leveraging topological structures in the modeling and analysis of strategic games.

Through a review of existing literature and a critical analysis of the current state of research in the field, this study aims to position itself at the forefront of exploring the intersection of game theory and topology, offering new insights into strategic decision-making, optimal strategies, and game dynamics within the realm of topological spaces.

By exploring the intersection of the Banach-Mazur game on a topological space [4] and optimal control theory [5], a fresh perspective emerges on strategic game modeling in the context of topological spaces [6]. The game, where players strategically select nested open sets to influence the intersection, reflects a strategic battle in a topological domain. Its outcome hinges on whether the space is a Baire space¹, showcasing strategic advantages through dense open set intersections.

This connection to optimal control theory reveals a profound link between game strategies and control systems. Optimal control theory's objective of finding the best control law parallels crafting winning strategies in the Banach-Mazur game. The interaction between Player I (the Controller) minimizing costs and Player II (Nature) introducing uncertainties resonates with the challenge of managing a system amidst disturbances.

This relationship extends to state spaces in control systems, where the evolution of states under control actions mirrors the progression of nested open sets in the Banach-Mazur game. Developing effective control laws to guide system trajectories aligns with formulating winning strategies in the game. Moreover, Baire space properties not only secure winning strategies in the game but also reflect robust control tactics in practical systems, ensuring stability and performance despite external disruptions. [7]

3. Conceptual Framework

The Banach-Mazur game provides valuable insights into the correlation between game strategies and optimal control amidst uncertainties. Baire space properties underscore the significance of robust strategies in both realms, emphasizing the critical role of topological concepts in maintaining system stability and performance in control theory. This innovative approach sheds light on the intricate dynamics of strategic game modeling in topological spaces, bridging the gap between game theory and control systems within a unified mathematical framework.

By building a robust mathematical framework and model that captures the essence of the Banach-Mazur game, optimal control theory, and topological concepts, we can explore the intricate dynamics of strategic decision-making in control systems and advance the understanding of how game theory principles can be applied to optimize system behavior in the presence of uncertainties.

In game theory, equilibrium refers to a state where each player's strategy is optimal given the strategies of the other players. One of the most well-known equilibrium concepts is the Nash equilibrium, named after John Nash, which is a set of strategies, one for each player, such that no player has an incentive to unilaterally change their strategy.

Mathematically, a Nash equilibrium can be defined as a set of strategies (one for each player) in which each player's strategy is a best response to the strategies chosen by the other players. More formally, let's consider a game with n players. Denote the strategy sets of the players by S1, S2,..., Sn, and let si denote the strategy of player i. The payoff function of player i, denoted by ui(si, s-i), represents the utility or payoff player i receives when choosing strategy si while the other players choose strategies s-i.

A Nash equilibrium is a set of strategies s* = (s1, s2,..., sn) such that for each player i: ui(si, s*-i) ≥ ui(si, s*-i) for all si in Si, i = 1, 2,..., n.

In the context of topological games, where strategies can be represented as points in a topological space, the existence of Nash equilibria can often be established using fixed-point theorems from topology. Fixed-point theorems guarantee the existence of points in a space that do not move under a certain mapping.

One example of a fixed-point theorem commonly used in game theory is Brouwer's² Fixed-Point Theorem [8]. This theorem states that any continuous function from a compact, convex set to itself must have a fixed point. In game theory, this can be interpreted as guaranteeing the existence of a strategy profile where no player has an incentive to unilaterally deviate from their strategy.

In the context of a topological game, when the strategy space is a compact topological space and the payoff functions are continuous, the existence of a Nash equilibrium can be established by applying Brouwer's Fixed-Point Theorem.

Overall, the mathematical model for equilibrium in game theory involves defining the players' strategy sets, payoff functions, and the conditions under which each player's strategy is optimal given the strategies of others. The concept of Nash equilibrium and the application of fixed-point theorems from topology play a crucial role in proving the existence of equilibria in games with strategies represented as points in topological spaces.

The Banach-Mazur game is a topological game that is played on a topological space X. The game involves two players, Player I and Player II, who take turns selecting non-empty open sets in such a way that the open sets chosen by Player I have to be nested within each other (i.e., 𝑈𝑛+1⊂𝑈𝑛).

The objective of Player I is to ensure that the intersection of all the selected sets is empty, while Player II aims to prevent this by strategically choosing open sets. Player I wins the game if the intersection of all the open sets chosen by both players is empty; otherwise, Player II wins. Mathematically, we can formalize the Banach-Mazur game as follows:

Let X be a topological space.

Player I selects a non-empty open set 𝑈1⊂𝑋

Player II, in response, selects a non-empty open set 𝑈2⊂𝑈1.

The players continue this process, with Player I selecting 𝑈3⊂𝑈2 and so on.

The outcome of the game depends on the properties of the topological space X. In particular, the game is often used to characterize Baire spaces. A Baire space is a topological space such that the intersection of countably many dense open sets is also dense.

Player II has a winning strategy in the Banach-Mazur game if and only if the topological space X is a Baire space. This result highlights the connection between topological properties of a space, such as being a Baire space, and the existence of winning strategies in the Banach-Mazur game.

Modeling framework:

In the Banach-Mazur game G(X) played on a topological space X, Player I and Player II take turns choosing nested open sets. Player I aims to make the intersection empty, while Player II aims to keep it non-empty, akin to a battle of control and strategy in a topological setting. The game's outcome is tied to whether X is a Baire space, where the intersection of dense open sets reflects the strategic advantage.

Optimal Control Theory Connection:

Optimal control theory seeks the best control law for a system to optimize a specific criterion. The Banach-Mazur game's strategies and outcomes can be linked to control systems through the state-space analysis and control strategies employed.

Control Systems and State Spaces:

Considering a typical control system described by a differential equation, the state x(t) and control u(t) govern the system's behavior. The aim is to find the control u(t) that minimizes a cost functional over a given time period, reflecting the optimal control strategy.

Game-Theoretic Interpretation:

In the optimal control setup, Player I (the Controller) selects actions to minimize costs, while Player II (Nature) introduces uncertainties that influence the system's response. This mirrors the dynamic interplay between controlling a system and adapting to uncertainties or disturbances.

Topological Game and Optimal Strategies:

Drawing analogies between the Banach-Mazur game and optimal control reveals a deep connection. The evolving state space under control actions aligns with the progression of nested open sets. Developing winning strategies in the Banach-Mazur game mirrors crafting optimal control laws to steer system trajectories effectively.

Baire Spaces and Robust Control:

Baire space properties not only ensure Player II's winning strategies in the Banach-Mazur game but also reflect robust control strategies in real-world systems. Robust control tactics aim to maintain system stability and performance despite external disturbances, reflecting the essence of Baire space properties.

4. Mathematical Model Development

1. System Dynamics - State Equation: The system dynamics are described by the state equation: 𝑥′(𝑡)=𝑓(𝑥(𝑡), 𝑢(𝑡)) where:

ο 𝑥(𝑡)∈𝑋 represents the state of the system at time 𝑡,

ο 𝑢(𝑡)∈𝑈 denotes the control input,

ο 𝑓 is the dynamics function that governs the evolution of the state based on the current state 𝑥(𝑡) and the control input 𝑢(𝑡)

2. Cost Functional - Objective Function: The objective function, or cost functional to be minimized, is defined as: 𝐽(𝑢)=∫0𝑇𝐿(𝑥(𝑡), 𝑢(𝑡)) 𝑑𝑡+𝜙(𝑥(𝑇)), where:

ο 𝐿 (𝑥, 𝑢) is the running cost function that quantifies the cost incurred at each time instant based on the state 𝑥(𝑡)x(t) and control input 𝑢(𝑡),

ο 𝜙(𝑥) is the terminal cost function that captures the cost associated with the final state 𝑥(𝑇) at the end time 𝑇,

ο The integral term represents the cumulative running cost over the time horizon [0, 𝑇],

ο The goal is to find the control input function 𝑢(𝑡) that minimizes this cost functional.

3. Banach-Mazur Game Interpretation: The optimal control problem is viewed as a game between two players - the Controller and Nature:

ο Controller (Player I): Selects control actions 𝑢(𝑡) to minimize the cost functional 𝐽(𝑢).

ο Nature (Player II): Represents uncertainties or disturbances that influence the state evolution, challenging the system's response.

ο The game unfolds in the state space 𝑋 and control space 𝑈, with strategic decision-making between the players influencing system dynamics.

4. Optimal Control Strategy: The optimal control strategy emerges as the solution that minimizes the overall cost 𝐽(𝑢) while ensuring system stability, desired performance, and robustness against uncertainties introduced by Nature.

5. Analytical Framework: The mathematical model provides a rigorous framework for analyzing and solving the optimal control problem within the game-theoretic perspective, leveraging concepts from topological spaces, strategic decision-making, and system dynamics.

To illustrate the correlation between control space and topology space in the context of game theory, let's focus on how these concepts relate to our previous examples. We'll highlight the continuous nature of both the strategy and control spaces and show their relationship through a geometric representation.

5. Control Space and Topology Space

Control Space: In optimal control theory, the control space represents the set of all possible control actions that can be applied to a dynamical system. These controls are typically chosen to optimize a performance criterion over time.

Topological Space: A topological space is a set equipped with a topology, which defines how elements of the set relate to each other in terms of continuity, convergence, and neighborhood structure. In the context of games, a topological strategy space allows for continuous choices of strategies.

6. Correlation and Relation

1. Continuous Strategy and Control Spaces:

n Both control and strategy spaces can be represented as continuous intervals or more complex topological spaces.

n Continuous functions can describe payoffs in games and performance criteria in control problems.

2. Optimization:

n In games, players optimize their payoffs by choosing optimal strategies.

n In control theory, the controller optimizes a performance criterion by selecting the best control actions.

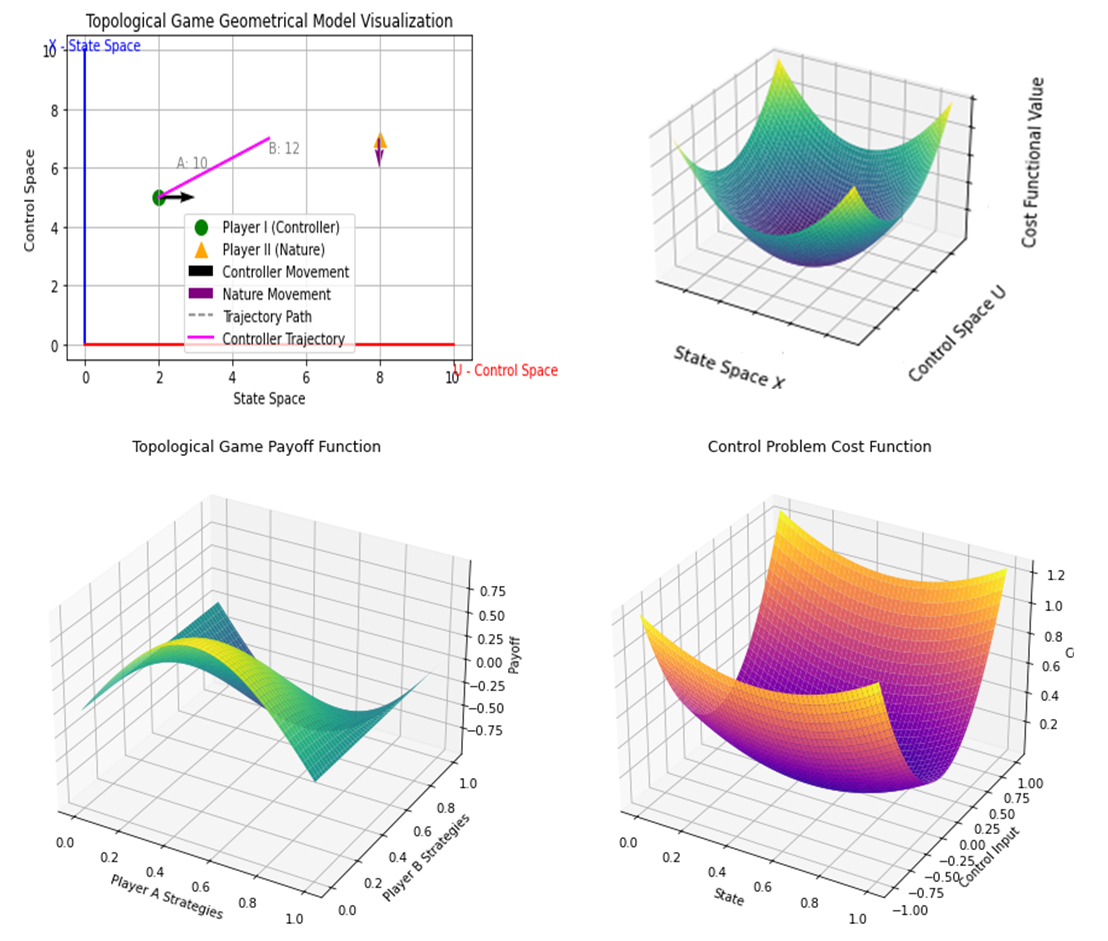Figure 1

7. Relationships

1. Continuous Spaces:

ο Both the strategy space in the game and the control space in the control problem are continuous intervals.

ο The payoff function in the game and the cost function in the control problem are continuous functions.

2. Optimization Goals:

ο In the game, players aim to maximize their payoffs by choosing optimal strategies.

ο In the control problem, the controller aims to minimize the cost function by choosing optimal control inputs.

3. Geometric Representation:

ο The 3D plots show how payoffs and costs vary smoothly with changes in strategies and control inputs.

ο The topological game and the control problem are visualized using similar geometric methods, highlighting their underlying connection through continuous spaces and optimization.

8. Strategic Interactions in Topological Spaces

Suppose that X be a topological space representing the game setting, and Assume T₁ and 𝑇₂ be two distinct topologies on X, denoted as (𝑋, 𝑇₁) and (𝑋, 𝑇₂) respectively. The strategic interactions within the game are modeled by players making decisions based on the topological properties of the space.

Consider a sequence of games played on 𝑋 with varying degrees of connectivity, where each game is associated with a specific topology 𝑇𝑖 on 𝑋 for 𝑖=1,2, … The players strategically interact within the topological context, adapting their decision-making strategies based on the connectivity and spatial relationships induced by the corresponding topology.

Introducing different topological structures or constraints 𝐶𝑖 within each game instance provides a framework for exploring how varying connectivity and spatial configurations influence strategic decision-making and outcomes. By analyzing the impact of these structural changes on game dynamics, players can develop adaptive strategies to navigate the topological environment effectively.

Furthermore, investigating the effects of dynamic topological changes or constraints 𝐷𝑡 during gameplay introduces a dimension of evolution in the game setting. Players must adjust their decision-making processes in response to fluctuating topological conditions, leading to the emergence of adaptive strategies and the evolution of optimal control tactics.

Through a rigorous examination of how players adapt their strategies in response to changing topological environments or constraints, new theoretical propositions or theorems can be derived that contribute to a deeper understanding of strategic game modeling within the context of topological spaces. This exploration sheds light on the intricate interplay between connectivity, spatial relationships, and strategic decision-making in abstract game scenarios, paving the way for new insights and advancements in the field of game theory and topology.

By transitioning from Euclidean to topological spaces and introducing control spaces, we gain a more comprehensive understanding of continuous optimization problems in both game theory and control theory.

9. Conclusions

By extending the concepts of Euclidean games to topological spaces and incorporating optimal control theory, we gain a deeper and more versatile understanding of strategic interactions and decision-making. Game theory in topological spaces is a rich and complex field that bridges abstract mathematical theory with practical applications in economics, algorithm design, machine learning and beyond.

By leveraging the tools of topology, researchers can gain deeper insights into the structure and outcomes of strategic interactions in various settings.

The detailed mathematical model of the Banach-Mazur game highlights the interplay between topological properties and game strategies. In optimal control theory, this interplay manifests in ensuring system trajectories meet desired criteria despite uncertainties. The Baire space properties guarantee robust strategies, similar to optimal controls ensuring stability and performance in control systems.

This framework opens up numerous avenues for further research and practical applications in various fields. The intricate mathematical model of the Banach-Mazur game sheds light on the parallels between game strategies and optimal control in navigating uncertainties. Baire space properties reinforce the importance of robust strategies in both scenarios, emphasizing the critical role of topological concepts in ensuring system stability and performance in the realm of control theory.

Notes

1. For the concept in topology, see Baire space, A topological space X is said to be a Baire space if every countable union of closed nowhere dense sets in X has empty interior in X.

2. In topological games, the application of Brouwer's fixed point theorem can provide insights into the existence of equilibrium strategies and stable solutions in games played on continuous spaces.