-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2024; 13(2): 32-36
doi:10.5923/j.jgt.20241302.02
Received: May 18, 2024; Accepted: Jun. 20, 2024; Published: Jul. 27, 2024

Friendly Equilibria
Ezio Marchi
Director of Instituto de Matemática Aplicada San Luis, Universidad Nacional de San Luis, Ejército de los Andes 950, San Luis, Argentina
Correspondence to: Ezio Marchi, Director of Instituto de Matemática Aplicada San Luis, Universidad Nacional de San Luis, Ejército de los Andes 950, San Luis, Argentina.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In game theory there are many discussions about the concept of rationality. Theoretically these discussions are concerned with an appropriate mathematical concept which derives from the concept itself. In this paper we present a new way of looking rationality which is concerned with an external view of the rules of games. We prove the existence of these new friendly equilibrium and perturbed friendly equilibria.
Keywords: Equilibria, Friendly
Cite this paper: Ezio Marchi, Friendly Equilibria, Journal of Game Theory, Vol. 13 No. 2, 2024, pp. 32-36. doi: 10.5923/j.jgt.20241302.02.
1. Results
- The most important equilibrium of non-cooperative games is the Nash equilibrium point; the perfect equilibrium of Selten and proper equilibrium of Myerson are also considered important. Most authors of non-cooperative games study applications of these three equilibria. However, there was no plan to consider friends. In this work we emphasize this last concept that can be applied to problems of sociology, economics, mathematics, etc. In the future it can be thought that the existence of this friendly equilibria can be applied to the aforementioned balances. We prove the existence.Here we are going to introduce the general tools of the game. Consider an n-person game in normal form
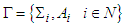 where the strategy sets are non-empty and finite. The mixed extension is
where the strategy sets are non-empty and finite. The mixed extension is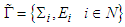 Now for a player consider a finite sequence of players
Now for a player consider a finite sequence of players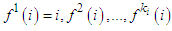 which we call the “successor friends” of player
which we call the “successor friends” of player 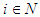 . Then from an intuitive point of view it is natural to assume that the player
. Then from an intuitive point of view it is natural to assume that the player 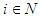 is “rational”: whenever his payoff is the same he is going to act in such way that first he will maximize the payoff of his first successor friend
is “rational”: whenever his payoff is the same he is going to act in such way that first he will maximize the payoff of his first successor friend 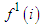 . In the case that the payoff of this successor friend
. In the case that the payoff of this successor friend 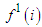 is equal again he will act to maximize the payoff of his second successor friend
is equal again he will act to maximize the payoff of his second successor friend 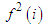 and so on until the last
and so on until the last 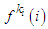 .Consider for
.Consider for 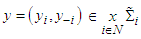 the sets
the sets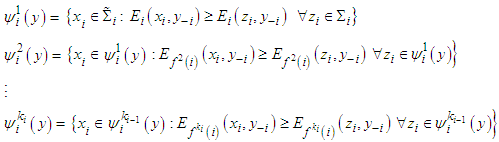 Formally we define a friendly equilibrium point if
Formally we define a friendly equilibrium point if 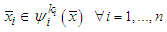 .Theorem 1: Given any game
.Theorem 1: Given any game 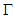 and
and 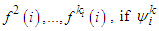 is upper semi-continuous for each
is upper semi-continuous for each 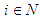 , there always exists a friendly equilibrium.Proof: given any point
, there always exists a friendly equilibrium.Proof: given any point  consider the set of points
consider the set of points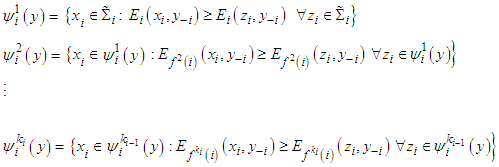 since the expectations are multi-linear then each
since the expectations are multi-linear then each 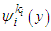 is non-empty convex and compact. Moreover, by the continuity of the expected functions and the hypothesis such,
is non-empty convex and compact. Moreover, by the continuity of the expected functions and the hypothesis such, 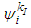 are upper semi-continuous. Therefore using Kakutani’s fixed point applied to
are upper semi-continuous. Therefore using Kakutani’s fixed point applied to 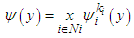 there exists a fixed point
there exists a fixed point 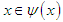 . Such point is a friendly equilibrium (q.e.d.).As a simple observation we would like to point out that in the case that
. Such point is a friendly equilibrium (q.e.d.).As a simple observation we would like to point out that in the case that 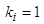 for each
for each 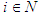 our new notion coincides with the fundamental Nash equilibrium points.It is interesting to remark that the existence of a friendly equilibrium is equivalent to the existence of a solution
our new notion coincides with the fundamental Nash equilibrium points.It is interesting to remark that the existence of a friendly equilibrium is equivalent to the existence of a solution 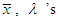 of the non-linear system
of the non-linear system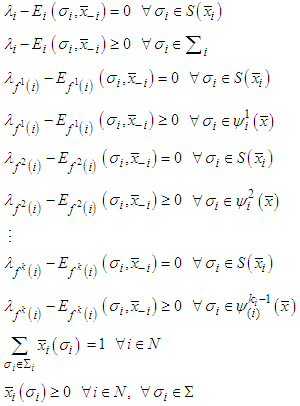 where
where 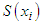 denotes the discrete support of
denotes the discrete support of 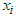 . The proof of the equivalence is rather easy and is left to the reader.
. The proof of the equivalence is rather easy and is left to the reader.2. Perturbed Friendly Equilibria
- Now we will extend the concept of friendly equilibria to the theory of perturbed equilibria. For this, we will follow the approaches of Selten (1975) and Myerson (1978).Consider a point
 such that it satisfies
such that it satisfies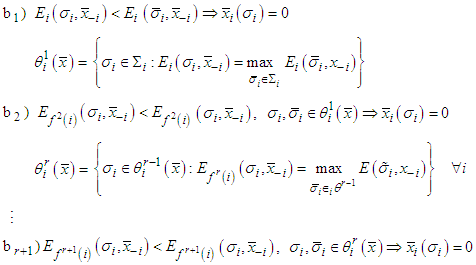 Theorem 2: A point is a friendly equilibrium point if and only if it fulfills B) with
Theorem 2: A point is a friendly equilibrium point if and only if it fulfills B) with 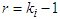 for each
for each 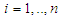 .Proof: We prove it by induction on
.Proof: We prove it by induction on 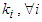 . For the case
. For the case  for each
for each 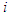 , this is very well known. Assume that it is valid for
, this is very well known. Assume that it is valid for 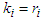 , then we will show that it is also valid for
, then we will show that it is also valid for 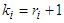 .For this, consider that
.For this, consider that 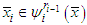 for each
for each 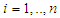 . Suppose that for
. Suppose that for 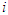
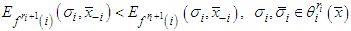 and
and 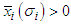 Let
Let 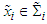 be the point defined as
be the point defined as 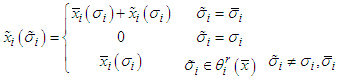 then
then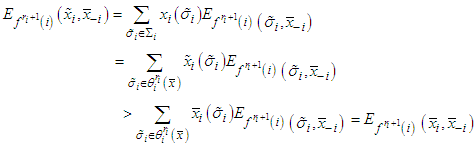 which is impossible since
which is impossible since 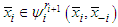 and
and 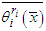 is identified with
is identified with 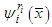 .Inversely, consider a point
.Inversely, consider a point 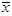 such that
such that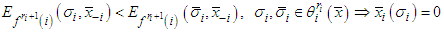 for each
for each 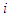 , then
, then 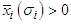 only if
only if 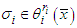 and
and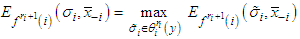 therefore
therefore 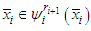 for each
for each 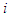 .Then following the ideas of Selten (1975), we define a perfect friendly equilibrium as follows: given
.Then following the ideas of Selten (1975), we define a perfect friendly equilibrium as follows: given 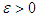 , a point
, a point 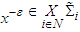 is called a
is called a 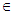 -perfect friendly equilibria if
-perfect friendly equilibria if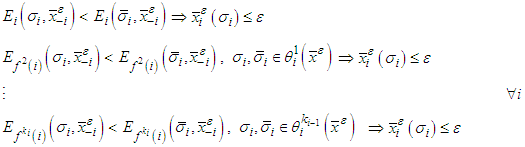 A perfect friendly equilibrium is a limit point of a sequence
A perfect friendly equilibrium is a limit point of a sequence 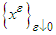 where
where 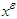 is an
is an 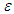 -perfect friendly rational equilibria. Similarly following the ideas of Myerson (1978) we define
-perfect friendly rational equilibria. Similarly following the ideas of Myerson (1978) we define 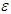 -proper friendly equilibria as
-proper friendly equilibria as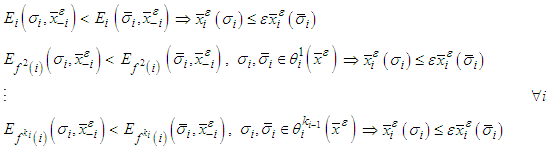 Clearly an
Clearly an 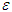 -proper friendly equilibrium is an
-proper friendly equilibrium is an 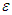 -perfect friendly equilibrium. A point
-perfect friendly equilibrium. A point 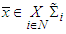 is called a proper friendly equilibria if
is called a proper friendly equilibria if  is a limit point of a sequence
is a limit point of a sequence 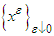 where
where 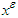 is an
is an 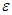 -proper friendly equilibrium.When
-proper friendly equilibrium.When 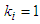 the
the 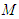 ’s corresponding concepts become the perfect and proper ones respectively.Theorem 3: Every normal form game possesses at least one proper friendly equilibrium if
’s corresponding concepts become the perfect and proper ones respectively.Theorem 3: Every normal form game possesses at least one proper friendly equilibrium if 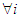 ,
, 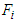 is upper semi-continuous.Proof: In order to prove this existence theorem let us observe that for given positive integers
is upper semi-continuous.Proof: In order to prove this existence theorem let us observe that for given positive integers 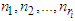 it always holds true
it always holds true 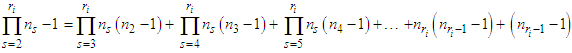 This can be proven by induction on
This can be proven by induction on 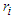 , which we skip. Therefore, it is clear that
, which we skip. Therefore, it is clear that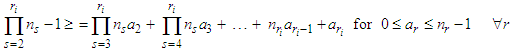 Now given
Now given 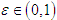 , define
, define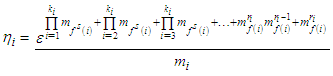 where
where 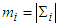 is the cardinality of
is the cardinality of 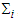 , and let
, and let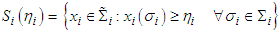 For
For 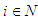 define the correspondence
define the correspondence 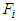 from
from 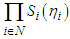 by:
by:
 We have that
We have that  is closed and convex for every
is closed and convex for every  and the mapping
and the mapping 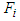 is upper semi-continuous. Now we will prove that
is upper semi-continuous. Now we will prove that 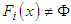 . Consider
. Consider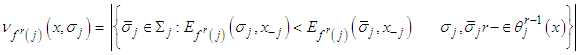 for all
for all 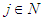 and
and 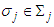 . Clearly
. Clearly 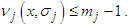 Let the point
Let the point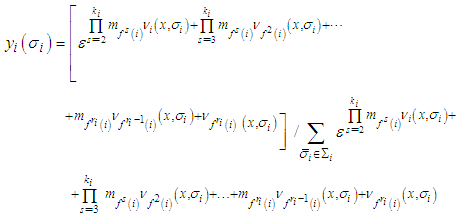 Clearly
Clearly 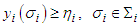 .Now if
.Now if 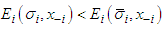 then
then 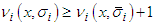 and
and 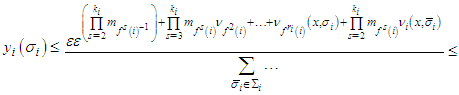 | (1) |
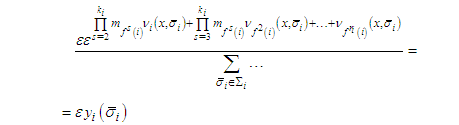 | (2) |
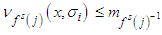 and the observation given above.Now if
and the observation given above.Now if 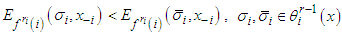 then all
then all 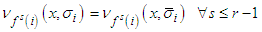 Then performing the same operation as before instead in, in, it is easy to see that
Then performing the same operation as before instead in, in, it is easy to see that 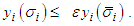 Let
Let 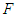 be the n-tuple
be the n-tuple 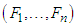 . Then it satisfies the condition of the Kakutani Fixed Point Theorem (Kakutani, 1941) and the fixed point of
. Then it satisfies the condition of the Kakutani Fixed Point Theorem (Kakutani, 1941) and the fixed point of 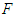 is an
is an 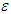 -proper friendly equilibrium. Now for
-proper friendly equilibrium. Now for 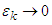 each
each 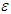 we have an
we have an 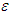 -proper friendly equilibrium, thus making
-proper friendly equilibrium, thus making 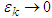 , it is always possible to find a converging subsequence since the space is compact. The limit point of such subsequence is a friendly equilibrium point. The proof is complete, then the theorem follows.As a simple consequence of this result we haveCorollary: Every normal form game has at least one perfect friendly equilibrium.Finally we would like to say that if the
, it is always possible to find a converging subsequence since the space is compact. The limit point of such subsequence is a friendly equilibrium point. The proof is complete, then the theorem follows.As a simple consequence of this result we haveCorollary: Every normal form game has at least one perfect friendly equilibrium.Finally we would like to say that if the 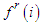 do not belong to
do not belong to 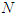 and are given externally, we have a external new notion of equilibrium. And we would like to emphasize that the previous material might be generalized accordingly for the continuous case. In this situation the upper semi-continuity condition appears more natural.
and are given externally, we have a external new notion of equilibrium. And we would like to emphasize that the previous material might be generalized accordingly for the continuous case. In this situation the upper semi-continuity condition appears more natural.ACKNOWLEDGMENTS
- I am great full for the collaboration of Miss Gimena Páez in editing and taping this paper.
Note
- 1. This paper was written in the year 1990 in a project supported by CONICET.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML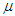 -subgame perfect equilibrium.
-subgame perfect equilibrium.