-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2024; 13(1): 15-20
doi:10.5923/j.jgt.20241301.03
Received: Jan. 29, 2024; Accepted: Feb. 23, 2024; Published: Mar. 4, 2024

The Fuzzy Prenucleolus II. Direct Existence Proofs, the Weakly Coalitional Monotonicity and a Characterization
Yeremia Maroutian
1806 Miles ave. Apt 112, Cleveland, OH, USA
Correspondence to: Yeremia Maroutian, 1806 Miles ave. Apt 112, Cleveland, OH, USA.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We give direct proofs of existence for the prenucleolus of fuzzy game for three different classes: strongly bounded; with lattice politopic sets of preimputations; and for the case when the game to solutions mapping possesses with continuous and monotonic selection functions. Generalized Zhou’s result on the weak coalitional monotonicity of fuzzy prenucleolies. In the last part we characterize fuzzy prenucleolies by four properties.
Keywords: Fuzzy prenucleolus, Fuzzy prenucleoli, Strongly bounded games, Lattice politopes
Cite this paper: Yeremia Maroutian, The Fuzzy Prenucleolus II. Direct Existence Proofs, the Weakly Coalitional Monotonicity and a Characterization, Journal of Game Theory, Vol. 13 No. 1, 2024, pp. 15-20. doi: 10.5923/j.jgt.20241301.03.
Article Outline
1. Introduction
- The optimality principle for TU games, which in game theory known as nucleolus has been introduced by D. Schmeidler (1969). Since then it has attracted many researchers working in field of cooperative games. E. Kohlberg (1971) has described new properties of the concept, by Megiddo N. (1974) proved its nonmonotonicity, L. Zhou (1991) had a paper about weak coalitional monotonicity (WCM) of nucleolus. Sobolev A. (1976), Potters J. (1991), Sniders C. (1995), Voorneveld M, Nouveland A. (1998), Orshan and Sudholter P. (2003), have works that characterize the decision rule through various sets of properties. After Aubin J.-P. (1981) introduced the fuzzy concept in game theory extension of existing in the classical theory decision rules to fuzzy cooperative games has become matter of principal importance. Core has been generalized by Aubin (1981) and Shapley value by Tsurumi et. al. (2001). Maroutian Y. (2017) has extended to fuzzy games classical nucleolus and in Maroutian Y. (2019) in a setting that varies of what described in Tsurumi et. al. (2001) generalized for the fuzzy case Shapley value. Section 2 devoted to preliminaries that are known from the classical theory and the background material. The latter mostly refers to inductively defined sets [
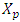 ,
, 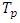 ]. That inductive process after finite number of steps provides with prenucleolus. There are direct existence proofs of prenucleolus in Section 3. For three different classes of games: strongly bounded games, games with lattice polytopic sets of preimputations and for belonging to same class games but possess with certain continuous selection functions we give direct existence proofs for the prenucleolus. In section 4 we extend to fuzzy games result of L. Zhou on weak coalitional monotonicity of prenucleolus (WCM).Section 5 characterizes prenucleolus through four properties: Nonemptiness, WCM, Consistency and Converse Consistency.
]. That inductive process after finite number of steps provides with prenucleolus. There are direct existence proofs of prenucleolus in Section 3. For three different classes of games: strongly bounded games, games with lattice polytopic sets of preimputations and for belonging to same class games but possess with certain continuous selection functions we give direct existence proofs for the prenucleolus. In section 4 we extend to fuzzy games result of L. Zhou on weak coalitional monotonicity of prenucleolus (WCM).Section 5 characterizes prenucleolus through four properties: Nonemptiness, WCM, Consistency and Converse Consistency.2. Preliminaries and Background
- Nucleolus of a classical cooperative game
 is an imputation that is the best in sense of some preference relation
is an imputation that is the best in sense of some preference relation 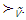 Let for game
Let for game 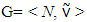
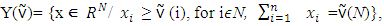 is the set of all imputations for game G.By magnitude
is the set of all imputations for game G.By magnitude  denotes excess of coalition S from vector x. Vector of excesses
denotes excess of coalition S from vector x. Vector of excesses 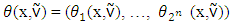 defined with components
defined with components  Clear that components of
Clear that components of 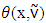 ordered decreasingly. On set
ordered decreasingly. On set  defined quasi-order
defined quasi-order  following way. For
following way. For 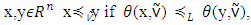 where
where  is for lexicographic order. That means exists a number
is for lexicographic order. That means exists a number 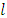 such that
such that  and
and 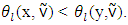 Definition. For
Definition. For  and characteristic function
and characteristic function  the set
the set 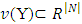 is nucleolus for Y if vectors from
is nucleolus for Y if vectors from 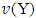 are minimal in sense of relation
are minimal in sense of relation  i.e.
i.e.  Theorem (Schmeidler (1969)) For every nonempty, convex and compact set the nucleolus exists and consists of only one vector. Theorem (Sobolev (1975)). Let for a game
Theorem (Schmeidler (1969)) For every nonempty, convex and compact set the nucleolus exists and consists of only one vector. Theorem (Sobolev (1975)). Let for a game 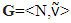 payoff vectors are preimputations from set
payoff vectors are preimputations from set 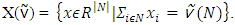 Then game G has a nonempty prenucleolus, which consists of only one vector.Due to violation of individual rationality for outcomes from
Then game G has a nonempty prenucleolus, which consists of only one vector.Due to violation of individual rationality for outcomes from 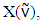 that set no more is compact and hence it is different of the set
that set no more is compact and hence it is different of the set 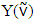 . Despite that, the statement on existence and uniqueness of prenucleolus keeps remaining true. For a fuzzy game
. Despite that, the statement on existence and uniqueness of prenucleolus keeps remaining true. For a fuzzy game 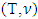 where
where  is the set of fuzzy coalitions let
is the set of fuzzy coalitions let  is the characteristic function of that game. Set of preimputations is the set of vectors that satisfy to condition of efficiency:
is the characteristic function of that game. Set of preimputations is the set of vectors that satisfy to condition of efficiency: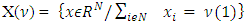 We inductively define sets
We inductively define sets  by accepting that
by accepting that 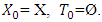 For
For  we define sets
we define sets 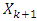 the following way:
the following way: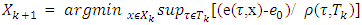 and sets
and sets 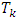 :
: where
where 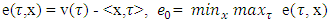 and
and  is the distance between point
is the distance between point 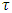 and set
and set 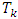 :
: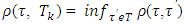 , where
, where  When k increases sets
When k increases sets  do not decrease:
do not decrease: 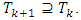 If for some
If for some  it turns out that
it turns out that  , then that in its turn entails stabilization of corresponding set
, then that in its turn entails stabilization of corresponding set 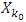 , or otherwise, with increasing of k
, or otherwise, with increasing of k 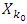 does not decrease any more. That kind of stabilization of sets
does not decrease any more. That kind of stabilization of sets  after finite number of minimization steps can happen in case of games with no piece-wice affine characteristic functions.Vectors from mentioned kind of sets
after finite number of minimization steps can happen in case of games with no piece-wice affine characteristic functions.Vectors from mentioned kind of sets 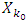 we call prenucleolies in different of unique vectors that are prenucleoluses.
we call prenucleolies in different of unique vectors that are prenucleoluses.3. Direct Existence Proofs
3.1. The Strongly Bounded Games
- Definition 3.1.1 A game
 is strongly bounded if there is a number M>0 such that for every vector
is strongly bounded if there is a number M>0 such that for every vector 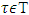 and coalition
and coalition 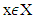 inner product
inner product  It is clear that for a strongly bounded game set of division vectors
It is clear that for a strongly bounded game set of division vectors  is compact and convex.Definition 3.1.2
is compact and convex.Definition 3.1.2  is a piece-wice linear characteristic function game if there is a collection of simplexes
is a piece-wice linear characteristic function game if there is a collection of simplexes 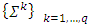 , such that for each i, j if
, such that for each i, j if 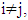
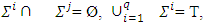 as well for
as well for 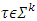 , where
, where  and
and 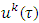 is a linear function.The following is a direct proof of existence of fuzzy prenucleolus for strongly bounded piece-wice linear characteristic function games.Theorem 3.1.1. A strongly bounded piece-wice linear characteristic function game possesses with a unique prenucleolus.Proof. Let the following equation holds true on some simplex
is a linear function.The following is a direct proof of existence of fuzzy prenucleolus for strongly bounded piece-wice linear characteristic function games.Theorem 3.1.1. A strongly bounded piece-wice linear characteristic function game possesses with a unique prenucleolus.Proof. Let the following equation holds true on some simplex 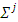 :
: 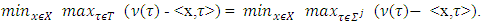 Below we deal with minimization problem (MP):
Below we deal with minimization problem (MP):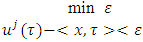 where
where 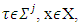 and
and 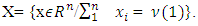 This problem has a solution because set X is a polytope. Solution of that minimization problem is the set:
This problem has a solution because set X is a polytope. Solution of that minimization problem is the set: 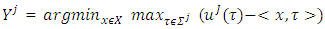
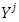 is a polytope because
is a polytope because 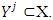 It also is convex and bounded. From there sets
It also is convex and bounded. From there sets  , where
, where 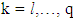 are compact and convex. For
are compact and convex. For  and
and  inner product
inner product 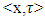 is a linear function of
is a linear function of  . Hence, instead of
. Hence, instead of 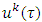 we can deal with inner product
we can deal with inner product  , where
, where 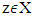 is some vector. Expression
is some vector. Expression  reaches at some coalition
reaches at some coalition  for every k. It is well known that
for every k. It is well known that  reaches only on extX. From there, as far as in the problem for
reaches only on extX. From there, as far as in the problem for  is the set of points of minimum for expression
is the set of points of minimum for expression 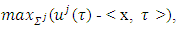 hence
hence 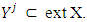 Because set of preimputations X is a polytope, so for a bounded game it also bounded, closed and convex. So is set ext X of X. The solution of MP can be represented by a mapping
Because set of preimputations X is a polytope, so for a bounded game it also bounded, closed and convex. So is set ext X of X. The solution of MP can be represented by a mapping 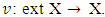 From
From 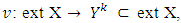 follows that
follows that  and for each
and for each 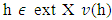 is a nonempty and convex set. So, according to Kakutani’s theorem mapping
is a nonempty and convex set. So, according to Kakutani’s theorem mapping 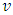 possesses with a fixed point, i.e. with an
possesses with a fixed point, i.e. with an 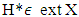 such that
such that 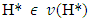 and
and  is a subset of set
is a subset of set 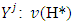
 From the written right now it follows that for
From the written right now it follows that for 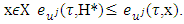 To conclude the proof remains to consider the case, when
To conclude the proof remains to consider the case, when 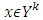 and
and 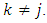 Started from some number m
Started from some number m  and as well
and as well  for arbitrary m. Holds true the inclusion:
for arbitrary m. Holds true the inclusion: 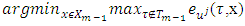
 Denote:
Denote:  and
and 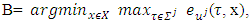 where
where  is an arbitrary number.Accept we have that
is an arbitrary number.Accept we have that 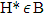 and
and 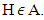 Due to inclusion above
Due to inclusion above 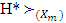 H. From there,
H. From there,  The latter one completes the proof that H* is the prenucleolus of game
The latter one completes the proof that H* is the prenucleolus of game 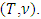
3.2. Games with Lattice Polytopic Sets of Preimputations
- In case of strongly bounded games set of preimputations to deal with obtains as a result of excluding from the initial set X big chunks of preimputations. This is a restrictive measure, which can cause fair objections. Dealing with games that have lattice polytopic sets of preimputations is a way for evading of blame. Definitions. For vectors
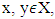 x preferable of y in sense of preference
x preferable of y in sense of preference 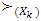 or
or  if there is a set
if there is a set  such that
such that 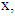
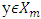 and for some
and for some 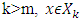 but
but 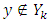 .All of the followed operations of ordering defined in sense of
.All of the followed operations of ordering defined in sense of 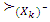 preference.For
preference.For  denotes least of upper bounds (biggest of lower bounds) of A in X. With respect to preference
denotes least of upper bounds (biggest of lower bounds) of A in X. With respect to preference 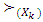 X is a partially ordered set (POS). A POS X is a join (meet) lattice if for every
X is a partially ordered set (POS). A POS X is a join (meet) lattice if for every 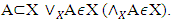 At this point we require that for our polytope X it’s set of peaks has been a join lattice in sense of preference
At this point we require that for our polytope X it’s set of peaks has been a join lattice in sense of preference  Theorem 3.2.1. A piece-wice linear characteristic function game
Theorem 3.2.1. A piece-wice linear characteristic function game 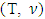 with a lattice polytope set of preimputations possesses with a unique prenucleolus.Proof. Let for a linear game
with a lattice polytope set of preimputations possesses with a unique prenucleolus.Proof. Let for a linear game 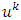 on
on  is the set of solutions of MP that corresponds to
is the set of solutions of MP that corresponds to 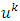 , i.e.
, i.e. and
and 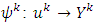 is a mapping. In difference of strongly bounded games sets
is a mapping. In difference of strongly bounded games sets 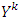 here not bounded and hence they are only closed and convex. Mapping
here not bounded and hence they are only closed and convex. Mapping  for games from this class can as well be represented as a mapping
for games from this class can as well be represented as a mapping  We have proved in the previous theorem that
We have proved in the previous theorem that  which means that
which means that 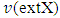 is a set of extreme points itself. Farther, we will deal with the least upper bound of set
is a set of extreme points itself. Farther, we will deal with the least upper bound of set 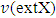 in sense of preference
in sense of preference 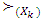 . We need to show that exists
. We need to show that exists  For the latter recall first what we have written related to mapping
For the latter recall first what we have written related to mapping 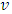 i. e
i. e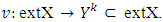 Then,
Then, 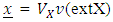 which is l.u.b. of set
which is l.u.b. of set 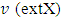 is sense of
is sense of 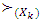 -preference also is l.u.b. for some set
-preference also is l.u.b. for some set  . Because for each
. Because for each 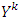 there is only one upper bound that belongs to
there is only one upper bound that belongs to  , hence due to closedness of
, hence due to closedness of 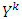 and linearity of excess as a function of
and linearity of excess as a function of 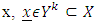 .Again for the reason that every
.Again for the reason that every 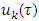 is a linear function, there is a
is a linear function, there is a 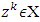 such that
such that 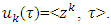 So for some numbers
So for some numbers 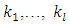 where
where  in representations of above linear functions for
in representations of above linear functions for 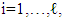 each one of
each one of 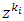 is a l.u.b. for set
is a l.u.b. for set  . The same
. The same 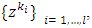 are as well fixed points for mappings
are as well fixed points for mappings 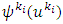 . Because
. Because 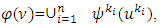 so from there
so from there 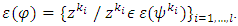 Prenucleolus is the only vector that is biggest in sense of
Prenucleolus is the only vector that is biggest in sense of 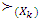 preference, or which is the same as it is vector
preference, or which is the same as it is vector 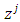 that minimizes expression
that minimizes expression 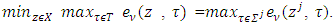 At the same time for some
At the same time for some 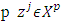 or
or  . To resume, vector
. To resume, vector 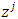 , which is the prenucleolus of
, which is the prenucleolus of 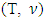 is the least of upper bounds for lattice polytope X and hence minimizes the expression with
is the least of upper bounds for lattice polytope X and hence minimizes the expression with 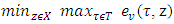 above.
above. 3.3. Mapping φ Possesses with Continuous Selection Functions
- Below we prove existence of prenucleolus in case when mapping
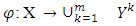 possesses with continuous selection functions. We assume as well that there are both kinds of them there: monotone increasing and decreasing.Definition 3.3.1 A mapping
possesses with continuous selection functions. We assume as well that there are both kinds of them there: monotone increasing and decreasing.Definition 3.3.1 A mapping  decreases (increases) if for
decreases (increases) if for 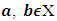 and
and  , from
, from 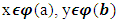 follows that
follows that 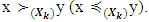 Definition 3.3.2. A selection function for a multivalued mapping
Definition 3.3.2. A selection function for a multivalued mapping 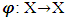 is a function
is a function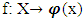 such that for every
such that for every 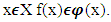 For the needs of this part we assume that the set of preimputations X endowed with sup norm topology. It is not worth a lot that in the definition of a game inherent a topological assumption regarding the payoff functions. We just need it to ensure the convergence of sequences
For the needs of this part we assume that the set of preimputations X endowed with sup norm topology. It is not worth a lot that in the definition of a game inherent a topological assumption regarding the payoff functions. We just need it to ensure the convergence of sequences 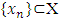 and continuity of selection functions for
and continuity of selection functions for  .The existence proof of prenucleolus becomes pretty direct for mapping
.The existence proof of prenucleolus becomes pretty direct for mapping 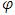 that possesses continuous, monotonic selection functions.Theorem 3.3.1. Let
that possesses continuous, monotonic selection functions.Theorem 3.3.1. Let 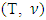 is a piece-wice linear characteristic function game, with a lattice polytope set of preimputations X, and
is a piece-wice linear characteristic function game, with a lattice polytope set of preimputations X, and 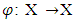 maps to
maps to  solutions of it’s MP’s. Then
solutions of it’s MP’s. Then 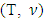 possesses with a unique prenucleolus if there are monotonic increasing and decreasing continuous selection functions for
possesses with a unique prenucleolus if there are monotonic increasing and decreasing continuous selection functions for 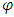 . Proof. First we prove existence of a fixed point for
. Proof. First we prove existence of a fixed point for  selection function f and then show not emptiness of
selection function f and then show not emptiness of 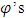 set of fixed points:
set of fixed points:  After what we show that the obtained this way fixed point, which contained in
After what we show that the obtained this way fixed point, which contained in  is greatest in sense of
is greatest in sense of  As we have mentioned that earlier,
As we have mentioned that earlier, 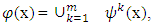 where
where  is the set of solutions of MP that corresponds to the game with simplex of fuzzy coalitions
is the set of solutions of MP that corresponds to the game with simplex of fuzzy coalitions 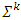 . Farther for
. Farther for 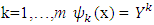 and
and 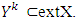 We separate two cases.Case 1. Let
We separate two cases.Case 1. Let  and
and  . As least upper bound of
. As least upper bound of  The monotone increase of argument x we consider in sense of preference
The monotone increase of argument x we consider in sense of preference 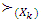 .Let for selection function f assume that it is continuous, monotonic increases and
.Let for selection function f assume that it is continuous, monotonic increases and  is a sequence of f -iterates from
is a sequence of f -iterates from 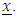 That means
That means 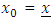 and
and  . From there,
. From there, 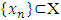 is a monotone increasing in sense of
is a monotone increasing in sense of  preference sequence. Since X is a lattice politope, so there is an upper bound of X, which bounds
preference sequence. Since X is a lattice politope, so there is an upper bound of X, which bounds  and from where
and from where 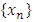 converges to a point
converges to a point 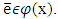 Because
Because  so due to continuity of f converge both of the sequences
so due to continuity of f converge both of the sequences 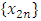 and
and 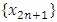 , which means that
, which means that  is a fixed point for f, i.e.
is a fixed point for f, i.e.  By the other side, because
By the other side, because 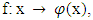 hence
hence 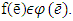 That in its turn means,
That in its turn means, 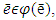 i.e. the same ē as well is a fixed point for
i.e. the same ē as well is a fixed point for  and set
and set  is not empty.Let now show that
is not empty.Let now show that 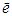 is the biggest fixed point in sense of preference
is the biggest fixed point in sense of preference  . Suppose that
. Suppose that 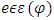 and
and  It is clear that
It is clear that  in the sense of
in the sense of 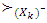 preference.Assume that f′ is a monotone decreasing selection function for
preference.Assume that f′ is a monotone decreasing selection function for  . Sequence of f′ - iterates of
. Sequence of f′ - iterates of 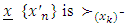 monotone decreasing. From there, for some number
monotone decreasing. From there, for some number  and for some other number
and for some other number 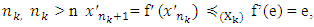 which again holds true due to continuity of f ’. By induction we obtain that
which again holds true due to continuity of f ’. By induction we obtain that  Hence, in this case
Hence, in this case 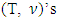 prenucleolus is fixed point
prenucleolus is fixed point 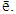 Case 2.
Case 2. 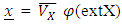 and
and  In this case
In this case  is the biggest point in
is the biggest point in 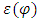 that can minimize the maximal excess. From there it is the prenucleolus of
that can minimize the maximal excess. From there it is the prenucleolus of 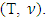 An example of a monotonic selection function. Example 3.3.1 Let
An example of a monotonic selection function. Example 3.3.1 Let 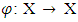 is a monotone decreasing mapping and for
is a monotone decreasing mapping and for 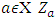 be the following set:
be the following set: 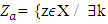 such that
such that 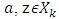 and
and 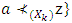
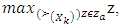 when
when 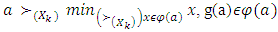
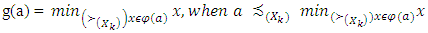 For
For 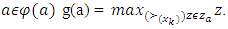 Defined this way function g(.) is a decreasing selection function for
Defined this way function g(.) is a decreasing selection function for 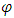 .Remark 3.3.1. In the example above if to replace the condition of monotonic decreasingness for mapping
.Remark 3.3.1. In the example above if to replace the condition of monotonic decreasingness for mapping 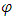 by the same kind of increasingness then function g(.) will become monotone increasing.
by the same kind of increasingness then function g(.) will become monotone increasing.4. The Weak Monotonicity Property of Fuzzy Prenucleolus
- Let
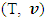 and (T, w) are two fuzzy games and
and (T, w) are two fuzzy games and 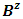 is a set of fuzzy coalitions such that
is a set of fuzzy coalitions such that and for
and for 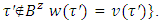 Denote by
Denote by  and
and 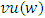 the sets of prenucleolies for games
the sets of prenucleolies for games 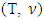 and
and 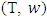 respectively.Definition. The fuzzy prenucleoli is weakly coalitionally monotonic if
respectively.Definition. The fuzzy prenucleoli is weakly coalitionally monotonic if 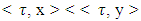 for
for 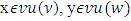 and
and  .The theorem below extends L. Zhu’s (1991) property of weak coalitional monotonicity for the classical prenucleolus on prenucleolies for fuzzy cooperative games. Theorem 4.1 For any fuzzy game its prenucleolies when they exist possess the property of weak coalitional monotonicity.Proof. Let construct
.The theorem below extends L. Zhu’s (1991) property of weak coalitional monotonicity for the classical prenucleolus on prenucleolies for fuzzy cooperative games. Theorem 4.1 For any fuzzy game its prenucleolies when they exist possess the property of weak coalitional monotonicity.Proof. Let construct 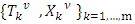 for game
for game  be such that it results to prenucleoli
be such that it results to prenucleoli  . Then there are sets
. Then there are sets  such that
such that 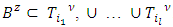 .Depending on if coalitions
.Depending on if coalitions 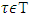 belong to set
belong to set  or not one can describe the containing them sets from these constructs as well their mutual locations in
or not one can describe the containing them sets from these constructs as well their mutual locations in 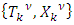 and
and  If
If 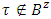 and for a vector
and for a vector 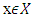 sets, for example
sets, for example  and
and  contain x then they coincide, because the vectors containing in both of the sets minimize equal excesses.Let now for a coalition
contain x then they coincide, because the vectors containing in both of the sets minimize equal excesses.Let now for a coalition 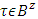 discuss first it’s mutual positions in constructs
discuss first it’s mutual positions in constructs  and
and 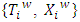 . It is clear that there is a number j such that
. It is clear that there is a number j such that 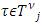 . Because
. Because 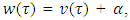 so the position of coalition
so the position of coalition 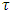 in construct
in construct  compared with the same in
compared with the same in  obtains by moving it up through the column of
obtains by moving it up through the column of 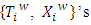 to a certain set
to a certain set  , where
, where  Set
Set 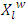 that corresponds to
that corresponds to 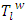 consists of vectors minimizing the excess of coalition
consists of vectors minimizing the excess of coalition 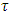 in game
in game 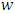 . Therefore if
. Therefore if  and
and 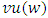 are prenucleolies of games
are prenucleolies of games 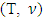 and
and  respectively and
respectively and  then for
then for 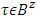 such that
such that 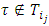
 From there it follows that
From there it follows that  Remark 4.1 The proved property remains true as well in the case when a game possesses with prenucleolus. Remark 4.2 When set
Remark 4.1 The proved property remains true as well in the case when a game possesses with prenucleolus. Remark 4.2 When set 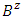 contains as well classical coalitions then inequality obtainedabove this time refers also to coalitions
contains as well classical coalitions then inequality obtainedabove this time refers also to coalitions 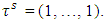 For
For 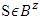 we receive Zhou’s classical property of weak coalitional monotonicity i.e.,
we receive Zhou’s classical property of weak coalitional monotonicity i.e.,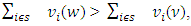 when
when 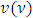 and
and 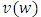 instead are prenucleoluses and v,w are piece-wice affine games.
instead are prenucleoluses and v,w are piece-wice affine games. 5. A Characterization of Fuzzy Prenucleolies
5.1. Some Preliminaries
- For
 we denote by
we denote by  the set of all fuzzy coalitions that belong to cube
the set of all fuzzy coalitions that belong to cube  . To a
. To a 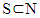 corresponds fuzzy coalition
corresponds fuzzy coalition 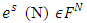 , which is the vector
, which is the vector 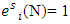 if
if 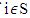 and
and 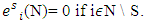 Fuzzy coalition
Fuzzy coalition 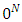 corresponds to the empty player coalition. We denote by
corresponds to the empty player coalition. We denote by  the class of all fuzzy games
the class of all fuzzy games  that possess with prenucleolies. For a game
that possess with prenucleolies. For a game 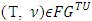 a payoff vector is a function
a payoff vector is a function 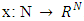 . x is efficient
. x is efficient  if
if 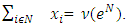 The set of preimputations of
The set of preimputations of 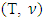 is:
is:  Restriction of payoff vector x to S is vector
Restriction of payoff vector x to S is vector 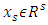 and for
and for 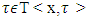 denotes inner product of vectors
denotes inner product of vectors 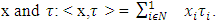
5.2. The Properties
- Below are the properties by what we are going to characterize fuzzy prenucleolies.P1. Non-emptiness (NEmpt.)P2. Weak coalitional monotonicity (WCM)P3. Consistency (Cons.)P4. Converse Consistency (ConCons)A solution on
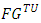 is a mapping
is a mapping 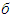 which associates with each game
which associates with each game 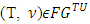 a set
a set 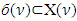 that satisfies to properties P1-P4. The domain for solution
that satisfies to properties P1-P4. The domain for solution  is the set of fuzzy games
is the set of fuzzy games 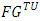 .As that proved in Maroutian Y. (2017) the minimization process by solving of linear programming problems (LPP) after finite number of steps provides with a single solution, which is the prenucleolus for piece-wice affine characteristic function games.For not piece-wice affine characteristic function games started from some step k solution of the corresponding MP may not decrease any more, i.e. may be
.As that proved in Maroutian Y. (2017) the minimization process by solving of linear programming problems (LPP) after finite number of steps provides with a single solution, which is the prenucleolus for piece-wice affine characteristic function games.For not piece-wice affine characteristic function games started from some step k solution of the corresponding MP may not decrease any more, i.e. may be 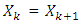 for following problem. Vectors that belong to stabilized this way sets
for following problem. Vectors that belong to stabilized this way sets 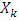 we call prenucleoli.We will use Y - A Hwang’s (2007) extension of classical reduced game to games from
we call prenucleoli.We will use Y - A Hwang’s (2007) extension of classical reduced game to games from 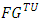 that has been introduced by Davis and Mashler (1965). Definition. Let
that has been introduced by Davis and Mashler (1965). Definition. Let  and
and  Reduced game with respect to S and x is
Reduced game with respect to S and x is 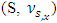 , where
, where 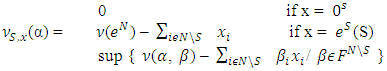 Below are definitions of properties P2-P4.• Consistency (cons.) If
Below are definitions of properties P2-P4.• Consistency (cons.) If  and
and 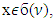 then
then  ,
, 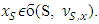 • Converse consistency (CCons.) If
• Converse consistency (CCons.) If  and
and 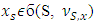 then
then  • Weak coalitional monotonicity (WCM).Let
• Weak coalitional monotonicity (WCM).Let  and
and 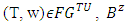 is a set of fuzzy coalitions defined in Part 4. If
is a set of fuzzy coalitions defined in Part 4. If 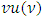 and
and 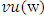 are prenucleolies of
are prenucleolies of 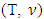 and
and  respectively, vectors
respectively, vectors  and
and 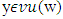 then fuzzy prenucleolies
then fuzzy prenucleolies 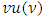 and
and  are weakly coalitionally monotonic if
are weakly coalitionally monotonic if 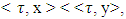 when
when 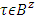 .As far as this property of fuzzy prenucleolies we have proved in the theorem of Part 4, so we will just refer to WCM without proving it again here.
.As far as this property of fuzzy prenucleolies we have proved in the theorem of Part 4, so we will just refer to WCM without proving it again here.5.3. The Results
- Lemma 5.3.1 Let
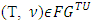 ,
, 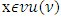 and
and 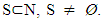 For arbitrary
For arbitrary  is the coalition of maximal excess then holds true following inequality
is the coalition of maximal excess then holds true following inequality Proof. Let
Proof. Let 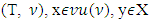 and
and 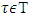 are the same as they are in lemma’s formulation. Then
are the same as they are in lemma’s formulation. Then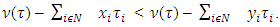 We need to show that if
We need to show that if  is an arbitrary coalition then
is an arbitrary coalition then 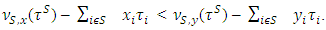 Accept that for some
Accept that for some 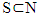 in contrary takes place the opposite inequality. By replacing in the inequality above first
in contrary takes place the opposite inequality. By replacing in the inequality above first 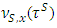 by it’s expression and then doing the same with
by it’s expression and then doing the same with  in case if takes place the opposite inequality then that would mean existence of a set
in case if takes place the opposite inequality then that would mean existence of a set 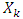 such that
such that 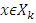 and at the same time for a
and at the same time for a 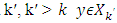 but
but  The latter one then would contradict to our assumption about vector x, i.e.
The latter one then would contradict to our assumption about vector x, i.e. 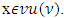 With this contradiction our lemma proves.Lemma 5.3.2. The prenucleolies satisfy consistency.Proof let
With this contradiction our lemma proves.Lemma 5.3.2. The prenucleolies satisfy consistency.Proof let 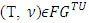 . For
. For 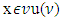 and
and 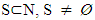 due to it’s definition
due to it’s definition 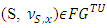 . In reduced game
. In reduced game 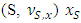 is efficient because of
is efficient because of  and definition of game
and definition of game  From there it remains to show that for all
From there it remains to show that for all 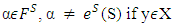 is an arbitrary vector then
is an arbitrary vector then 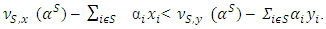 The latter one follows from lemma 5.3.1 and the inequality in its turn means that
The latter one follows from lemma 5.3.1 and the inequality in its turn means that  is a prenucleoli for
is a prenucleoli for 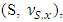 i.e.
i.e. 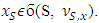 Lemma 5.3.3. prenucleolies satisfy to converse consistency. Proof. Let
Lemma 5.3.3. prenucleolies satisfy to converse consistency. Proof. Let  , with
, with  is prenucleoli of game
is prenucleoli of game 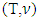 and vector
and vector 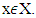 We assume that for all coalitions
We assume that for all coalitions 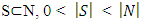 and for vector
and for vector 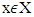 reduced game
reduced game i.e.
i.e. 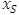 is a prenucleoli of
is a prenucleoli of 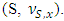 We need to prove that x is a prenucleoli for
We need to prove that x is a prenucleoli for 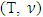 as well, i.e
as well, i.e 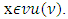 Let
Let  be an arbitrary vector and for
be an arbitrary vector and for 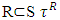 is the coalition of maximal excess in game
is the coalition of maximal excess in game 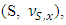 Then by Lemma 5.3.1
Then by Lemma 5.3.1 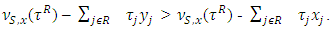 We need to show that for arbitrary
We need to show that for arbitrary 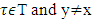
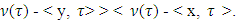 Otherwice, if there is
Otherwice, if there is 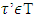 such that
such that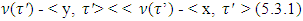 Then it would mean that for some coalition
Then it would mean that for some coalition 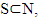 where
where 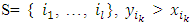 if
if 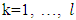 and hence for that coalition S in reduced game
and hence for that coalition S in reduced game  would not be it’s prenucleoli. The latter one violates precondition on converse consistency of
would not be it’s prenucleoli. The latter one violates precondition on converse consistency of  That means the inequality (5.3.1) is correct and x is a prenucleoli of game
That means the inequality (5.3.1) is correct and x is a prenucleoli of game 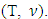 Farther we will prove the uniqueness. It based on Elevator Lemma introduced by Thomson (2005), The variant of this lemma we use says that if a solution б is consistent and on the subdomain of all proper games of
Farther we will prove the uniqueness. It based on Elevator Lemma introduced by Thomson (2005), The variant of this lemma we use says that if a solution б is consistent and on the subdomain of all proper games of  it is contained in a solution
it is contained in a solution 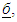 which is conversely consistent then the inclusion
which is conversely consistent then the inclusion 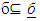 always holds.Theorem 5.1. A solution
always holds.Theorem 5.1. A solution 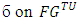 satisfies NEmpt., WCM, Cons. and CCons. if and only if for all
satisfies NEmpt., WCM, Cons. and CCons. if and only if for all 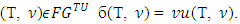 Proof. That
Proof. That  satisfies to NEmpt. follows from
satisfies to NEmpt. follows from 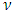 belongs to domain
belongs to domain 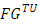 , where every game possesses with a set of prenucleolies. For each one of the rest of properties a corresponding statement we have proved.Assume that the solution
, where every game possesses with a set of prenucleolies. For each one of the rest of properties a corresponding statement we have proved.Assume that the solution 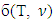 also in its turn satisfies to WCM, Cons, and CCons. Let
also in its turn satisfies to WCM, Cons, and CCons. Let 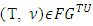 . To prove uniqueness we will use the method of induction on number
. To prove uniqueness we will use the method of induction on number 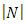 . For
. For 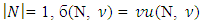 . Suppose that
. Suppose that 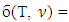
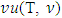 if
if 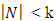 and
and 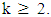 The case
The case  Let
Let 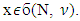 Based on Con. of
Based on Con. of 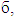 for all
for all 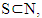 with
with 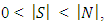
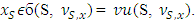 By CCon. of the prenucleoli
By CCon. of the prenucleoli  From there,
From there, 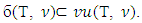 The inclusion
The inclusion  one can show by starting from
one can show by starting from  and come to
and come to  by applying similar proof. Hence,
by applying similar proof. Hence, 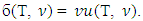
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML