-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2024; 13(1): 7-14
doi:10.5923/j.jgt.20241301.02
Received: Jan. 5, 2024; Accepted: Jan. 19, 2024; Published: Jan. 27, 2024

Optimizing Bioeconomic Models: A Comprehensive Approach Using the Jacobi Tau Method
Maan T. Alabdullah1, Esam A. El – Siedy1, Eliwa M. Roushdy2, Muner M. Abou Hasan3
1Department of Mathematics, Faculty of Science Ain Shams University, Egypt
2Department of Basic and Applied Sciences, Arab Academy for Science, Technology and Maritime Transport, Cairo, Egypt
3School of Mathematics and data science, Emirates Aviation University, Dubai, UAE
Correspondence to: Maan T. Alabdullah, Department of Mathematics, Faculty of Science Ain Shams University, Egypt.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This study introduces a novel (JTM) method for solving complex differential games. Our analysis demonstrates the superior accuracy and computational efficiency of JTM through optimal control problems involving nonlinear dynamics. Key results are presented through comparative performance indices, which reveal the JTM's potential to revolutionize numerical analysis and enhance simulation methodologies. This concise exploration opens new avenues for advanced research in applied mathematics and engineering.
Keywords: Jacobi Tau Method (JTM), Multi-Player Differential Games, Bioeconomic Models, Nash equilibrium, Optimal Control Theory, Mathematical Optimization in Economics
Cite this paper: Maan T. Alabdullah, Esam A. El – Siedy, Eliwa M. Roushdy, Muner M. Abou Hasan, Optimizing Bioeconomic Models: A Comprehensive Approach Using the Jacobi Tau Method, Journal of Game Theory, Vol. 13 No. 1, 2024, pp. 7-14. doi: 10.5923/j.jgt.20241301.02.
Article Outline
1. Introduction
- The resolution of intricate problems frequently involves the amalgamation of diverse mathematical frameworks and computational methods. In the domains of differential games and bioeconomic models, characterized by complex interactions and dynamic systems, the accuracy and computational efficiency of numerical methods are crucial. This imperative has catalyzed the investigation into novel computational strategies, including the application of the Jacobi Tau method (JTM) approach, which has shown promise in tackling differential equations that are nonlinear and subject to complex constraints.Differential game theory expands upon optimal control theory to examine the strategic interplay among several agents, each aiming to optimize their outcomes in the face of mutual competition. Recognized for its substantial influence in management sciences and economics, differential game theory’s applications permeate through various sectors, including resource management and the economics of ecosystems, as highlighted in foundational literature [1]. These applications range from marketing strategies to environmental economics and are further exemplified in studies on competitive dynamics in advertising [2] and the exploration of cooperative strategies within stochastic frameworks [3].Central to the study of differential games are equilibrium concepts. The Nash equilibrium serves as a cornerstone in concurrent games, where individual strategy adjustments cannot enhance outcomes [4]. Differential games, however, introduce a nuanced classification: closed-loop versus open-loop equilibria. Strategies in the former are contingent on both temporal and state variables, while in the latter, they depend solely on time and initial conditions. Identifying optimal strategies within such games requires solving a system of equations rooted in fundamental game theory principles, which delineate the optimal response strategies among players [5]. Various analytical and numerical methods are employed to find solutions to these equations [6].Given the limited availability of analytical solutions, numerical methods are indispensable for grappling with the complexities inherent in differential games. This area has been explored in depth, with studies ranging from linear quadratic dynamics ([7]-[11]) to nonlinear games addressing environmental concerns [12]. Certain scenarios, such as state-dependent scenarios [13] and zero-sum game frameworks [14], have further refined our understanding of equilibrium in differential games.Among various numerical techniques, spectral methods have been lauded for their precision and efficiency, leveraging orthogonal polynomial series to resolve differential equations ([15]-[19]). These methods, applied within the context of Pontryagin’s maximum principle, are particularly potent for differential games, with the choice of method being influenced by the nature of the differential game in question [20,21]. This research introduces a pioneering numerical scheme that synergizes Pontryagin’s maximum principle with the JTM approach to ascertain the (OLNE) in noncooperative, nonzero-sum differential games. In the confluence of mathematical theories, game theory, and computational analysis, the Jacobi Tau method approach emerges as a formidable tool, facilitating the transition from theoretical constructs to tangible, practical outcomes. This study ventures through the complexities of bioeconomic modeling and differential games, showcasing the potential of JTM to decode and address real-world economic and strategic challenges.The study employs the Jacobi Tau Method (JTM) in synergy with Pontryagin’s Maximum Principle to solve the OLNE in noncooperative nonzero-sum differential games. This approach illustrates the potential of JTM in addressing complex bioeconomic modeling and differential games, highlighting its capacity to handle real-world economic and strategic challenges.In summary, optimizing bioeconomic models involves a delicate balance of ecological sustainability, economic viability, and social acceptability. It requires an interdisciplinary approach that combines insights from biology, economics, mathematics, and social sciences. Advanced computational methods, like the Jacobi Tau Method, play a crucial role in addressing these challenges by providing more accurate and efficient tools for modeling and solving complex bioeconomic problems. In the realm of differential games and bioeconomic modeling, the Jacobi-Tau Method (JTM) stands out for its remarkable accuracy and computational efficiency, particularly when addressing complex interactions and dynamic systems. This method, developed to handle nonlinear differential equations and intricate constraints, shows a clear advantage over other methods like the Legendre Tau method. While the Legendre Tau method has been effective in solving open-loop Nash equilibrium problems in noncooperative games, the JTM's capability to handle more complex dynamics and constraints suggests a significant advancement in applied mathematics and engineering. Its potential in revolutionizing numerical analysis and enhancing simulation methodologies marks it as a promising tool for further research and applications in differential games and bioeconomic modeling, outperforming existing methods in key aspects.
2. Problem Statement
- In this segment, we address the dynamics of a four-player differential game characterized by noncooperative interactions and non-zero-sum payoffs as delineated below:
2.1. Definition
- We characterize a noncooperative nonzero-sum four-player differential game in the following manner [22]:
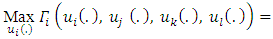
 subject to
subject to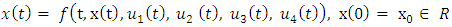 | (1) |
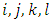 are indices that belong to the set {1, 2, 3, 4}, each one distinct from the others. Within the performance index
are indices that belong to the set {1, 2, 3, 4}, each one distinct from the others. Within the performance index  presented in (1), the functions
presented in (1), the functions 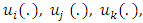 and
and 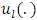 denote the control strategies employed by players
denote the control strategies employed by players 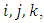 and
and  respectively; the function
respectively; the function 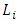 represents the immediate reward for player
represents the immediate reward for player 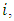 and
and  signifies the terminal reward. Each player’s objective is to optimize their respective performance indices through the strategic selection of their control actions
signifies the terminal reward. Each player’s objective is to optimize their respective performance indices through the strategic selection of their control actions  where
where  ranges from 1 to 4. The concept of an open-loop strategy refers to the predefined trajectory of a player’s actions over time [23]. This equilibrium notion is known for its temporal consistency, implying that no player has a reason to stray from their initial strategy as the game progresses. Consequently, we define an open-loop solution concept (equilibrium) as:
ranges from 1 to 4. The concept of an open-loop strategy refers to the predefined trajectory of a player’s actions over time [23]. This equilibrium notion is known for its temporal consistency, implying that no player has a reason to stray from their initial strategy as the game progresses. Consequently, we define an open-loop solution concept (equilibrium) as:2.2. Definition
- The collection of functions
 for each
for each 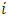 in 1, 2, 3, 4, constitutes an (OLNE) if, for any given
in 1, 2, 3, 4, constitutes an (OLNE) if, for any given 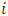 , there is an optimal control trajectory
, there is an optimal control trajectory  that resolves problem (1) and corresponds to the open-loop Nash strategy
that resolves problem (1) and corresponds to the open-loop Nash strategy 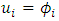 [1].The (OLNE) is defined by establishing Hamiltonian expressions to formulate the necessary first-order conditions for optimality in nonzero-sum differential games, indicated as (1). These expressions are introduced as follows [24]:
[1].The (OLNE) is defined by establishing Hamiltonian expressions to formulate the necessary first-order conditions for optimality in nonzero-sum differential games, indicated as (1). These expressions are introduced as follows [24]:  | (2) |
 within the set {1, 2, 3, 4}. Here, the variables
within the set {1, 2, 3, 4}. Here, the variables 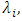 where
where 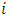 spans from 1 to 4, are known as the adjoint or costate variables that are paired with the state variable
spans from 1 to 4, are known as the adjoint or costate variables that are paired with the state variable 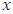 .For the sake of brevity in the Hamiltonian formulations, the time dependency in the variables
.For the sake of brevity in the Hamiltonian formulations, the time dependency in the variables 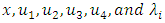 has been omitted. Given that all functions in (1) possess continuous derivatives, the primary conditions for an optimal solution are provided by the Pontryagin’s Maximum Principle. The Pontryagin’s Maximum Principle outlines the necessary conditions for an (OLNE) in a nonzero-sum differential game as follows:
has been omitted. Given that all functions in (1) possess continuous derivatives, the primary conditions for an optimal solution are provided by the Pontryagin’s Maximum Principle. The Pontryagin’s Maximum Principle outlines the necessary conditions for an (OLNE) in a nonzero-sum differential game as follows: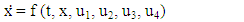 | (3) |
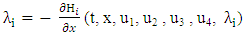 | (4) |
 | (5) |
 for every
for every  in {1, 2, 3, 4}. From the stationary condition (5), the control
in {1, 2, 3, 4}. From the stationary condition (5), the control  is derived as
is derived as  where
where  ranges from 1 to 4. Substituting this control into equations (3) and (4) leads to a set of differential equations solely in terms of
ranges from 1 to 4. Substituting this control into equations (3) and (4) leads to a set of differential equations solely in terms of  and
and 
 | (6) |
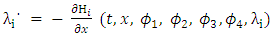 | (7) |
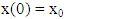 | (8) |
 | (9) |
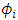 denoted as
denoted as  for each
for each  within 1, 2, 3, 4. In general, this set of Four-Point Boundary Value Problems (FPBVPs) tends to be nonlinear with mixed boundary conditions, making the precise analytical solution for the (OLNE) a complex task. This complexity necessitates the use of a suitable numerical technique for resolution.
within 1, 2, 3, 4. In general, this set of Four-Point Boundary Value Problems (FPBVPs) tends to be nonlinear with mixed boundary conditions, making the precise analytical solution for the (OLNE) a complex task. This complexity necessitates the use of a suitable numerical technique for resolution.3. Application of the Tau Technique in Multi-Player Differential Games
- This section details how the Tau technique can be utilized to solve the system of FPBVPs to ascertain the (OLNE) in a four-player nonzero-sum differential game. This method pivots on representing the function
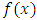 in
in 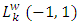 as a truncated series in the form:
as a truncated series in the form:  where
where 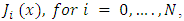 denote the Jacobi polynomials, while
denote the Jacobi polynomials, while 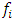 are the corresponding spectral coefficients. It should be noted that the omission of the temporal variable
are the corresponding spectral coefficients. It should be noted that the omission of the temporal variable 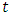 in subsequent discussions is meant for simplification. [25]
in subsequent discussions is meant for simplification. [25]3.1. Definition
- The set of Jacobi polynomials
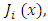 for
for 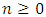 , is defined as a series of orthogonal polynomials over the interval [−1, 1] against the weigh.
, is defined as a series of orthogonal polynomials over the interval [−1, 1] against the weigh.  with
with 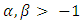 . The explicit form of these polynomials is given by the Rodrigues formula:
. The explicit form of these polynomials is given by the Rodrigues formula: 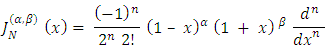
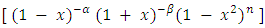 These polynomials encompass the Legendre polynomials for
These polynomials encompass the Legendre polynomials for 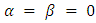 , the Chebyshev polynomials of the first and second kind for
, the Chebyshev polynomials of the first and second kind for 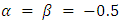 and
and  , respectively.
, respectively.3.2. Theorem
- Given
 within
within 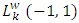 (a Sobolev space), the closest approximation.
(a Sobolev space), the closest approximation.  in the
in the 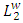 norm satisfies
norm satisfies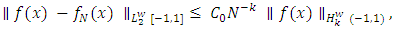 where
where  is a constant that depends only on the chosen norm, not on
is a constant that depends only on the chosen norm, not on 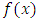 or
or 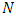 .Proof. Start by defining the Jacobi polynomial
.Proof. Start by defining the Jacobi polynomial 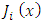 as follows:
as follows: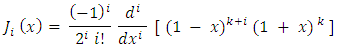 Next, we’ll use the properties of Jacobi polynomials to expand the error term
Next, we’ll use the properties of Jacobi polynomials to expand the error term 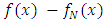 as a series of Jacobi polynomials:
as a series of Jacobi polynomials: 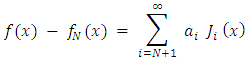 Where
Where 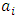 are the expansion coefficients given by:
are the expansion coefficients given by: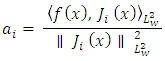 Here,
Here, 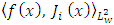 w represents the inner product of
w represents the inner product of 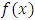 and
and 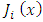 in the
in the 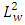 norm, and
norm, and 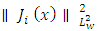 is the norm of
is the norm of  in the
in the  norm. Now, we’ll use the Sobolev space property to estimate
norm. Now, we’ll use the Sobolev space property to estimate 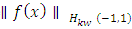 . The Sobolev norm is defined as:
. The Sobolev norm is defined as: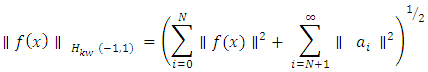 Using Cauchy-Schwarz inequality, we can bound
Using Cauchy-Schwarz inequality, we can bound 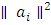 as follows:
as follows: Combining the expressions from the previous steps, we get:
Combining the expressions from the previous steps, we get:  We can bound
We can bound 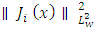 using properties of Jacobi polynomials and
using properties of Jacobi polynomials and 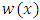 . Since
. Since  are orthogonal with respect to the weight function
are orthogonal with respect to the weight function  in the
in the 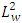 norm, we have:
norm, we have: 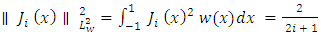 Plugging this result into the previous expression, we get:
Plugging this result into the previous expression, we get: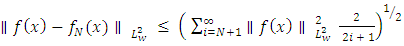 Now, we can estimate the sum in the above expression by an integral:
Now, we can estimate the sum in the above expression by an integral: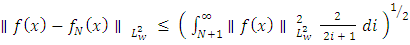 Since
Since  , we have
, we have  which means that
which means that  is bounded by
is bounded by 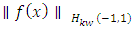 .Finally, we can simplify and bound the expression:
.Finally, we can simplify and bound the expression: This establishes the desired inequality:
This establishes the desired inequality: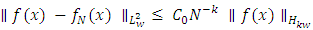 Where
Where 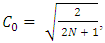 and the constant
and the constant  depends only on the chosen norm, not on
depends only on the chosen norm, not on  or
or 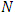 . This completes the proof of Theorem 3.2. As per Theorem 3.2, the convergence rate of the Jacobi polynomial approximation is
. This completes the proof of Theorem 3.2. As per Theorem 3.2, the convergence rate of the Jacobi polynomial approximation is  . The core principles and the convergence properties of the proposed method derive from the Jacobi Polynomial Approximation Theorem.
. The core principles and the convergence properties of the proposed method derive from the Jacobi Polynomial Approximation Theorem. 3.3. Theorem
- (Jacobi Polynomial Approximation Theorem) For any function f in
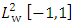 .and
.and  as a natural number, there exists a unique polynomial approximation
as a natural number, there exists a unique polynomial approximation 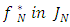 , the polynomial space of degree at most N with Jacobi polynomials, that minimizes the norm:
, the polynomial space of degree at most N with Jacobi polynomials, that minimizes the norm: where
where  is defined in terms of the orthogonal Jacobi polynomials
is defined in terms of the orthogonal Jacobi polynomials  as:
as: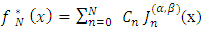 Here, the coefficients
Here, the coefficients  are determined by the inner product of
are determined by the inner product of 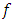 and the Jacobi polynomials:
and the Jacobi polynomials: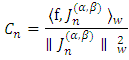 Proof. We aim to prove the existence and uniqueness of a polynomial
Proof. We aim to prove the existence and uniqueness of a polynomial 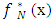 in
in 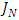 that minimizes the norm
that minimizes the norm 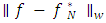 using Jacobi polynomials. We express
using Jacobi polynomials. We express  as a linear combination of the Jacobi polynomials
as a linear combination of the Jacobi polynomials 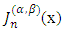 up to degree
up to degree 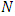 , i.e.,
, i.e., 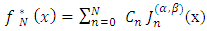 . To minimize
. To minimize 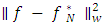 , where
, where we leverage the orthogonality property of Jacobi polynomials: if
we leverage the orthogonality property of Jacobi polynomials: if  then
then 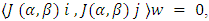 and if
and if 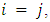 then
then 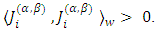 By taking derivatives with respect to
By taking derivatives with respect to 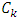 and setting them equal to zero, we find
and setting them equal to zero, we find 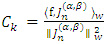 , yielding coefficients that minimize the norm and provide
, yielding coefficients that minimize the norm and provide  . To establish uniqueness, assuming two polynomials
. To establish uniqueness, assuming two polynomials 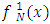 and
and  minimizing
minimizing 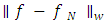 , we observe
, we observe 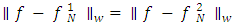 . After repeating the minimization process, we find that the coefficients for both polynomials are identical, confirming the uniqueness of the approximation. To adapt the Jacobi polynomials for the interval
. After repeating the minimization process, we find that the coefficients for both polynomials are identical, confirming the uniqueness of the approximation. To adapt the Jacobi polynomials for the interval 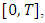 the domain is transformed by:
the domain is transformed by:  We approximate the solution functions
We approximate the solution functions  and
and 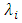 , with
, with 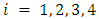 , for the FPBVPs by a sum of shifted Jacobi polynomials:
, for the FPBVPs by a sum of shifted Jacobi polynomials: | (10) |
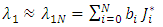 | (11) |
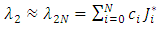 | (12) |
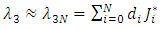 | (13) |
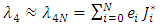 | (14) |
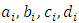 and
and 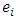 are coefficients to be determined, and
are coefficients to be determined, and 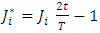 for
for 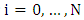 denote the shifted Jacobi polynomials on the interval [0, T].The approximate values for the first derivatives of
denote the shifted Jacobi polynomials on the interval [0, T].The approximate values for the first derivatives of  and
and 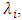 with
with 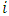 ranging from 1 to 4, are represented as:
ranging from 1 to 4, are represented as: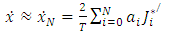 | (15) |
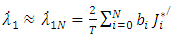 | (16) |
 | (17) |
 | (18) |
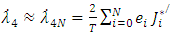 | (19) |
 | (20) |
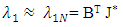 | (21) |
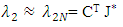 | (22) |
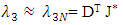 | (23) |
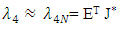 | (24) |
 | (25) |
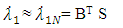 | (26) |
 | (27) |
 | (28) |
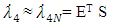 | (29) |
 and
and  denote the coefficient vectors, J* is the vector of modified Jacobi polynomials, and S represents the scaled derivatives of these polynomials. In the Tau method, one integrates these equations, substituting Equations (20) through (29) into the original differential equations to construct the residuals:
denote the coefficient vectors, J* is the vector of modified Jacobi polynomials, and S represents the scaled derivatives of these polynomials. In the Tau method, one integrates these equations, substituting Equations (20) through (29) into the original differential equations to construct the residuals: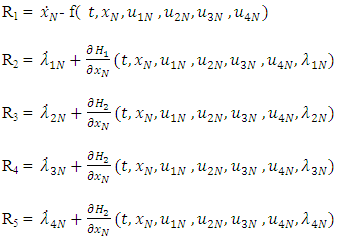 These residuals are minimized by multiplying them by
These residuals are minimized by multiplying them by 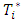 and integrating over the interval
and integrating over the interval 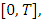 setting the result to zero, which leads to an algebraic system:
setting the result to zero, which leads to an algebraic system: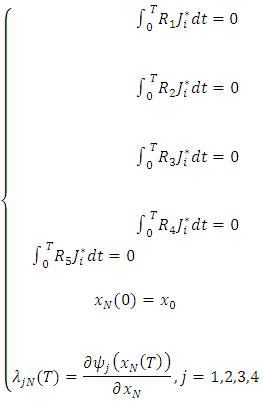 The coefficients of the vectors
The coefficients of the vectors 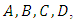 and
and 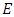 are determined by solving this system.
are determined by solving this system.4. Exemplary Demonstration
- This part evaluates the application of the Jacobi polynomial approach (JTM) on a bioeconomic model’s differential game to assess the method’s precision and computational effectiveness. In this ecological-economic context, four companies competitively exploit a shared regenerative natural asset (consider a fisheries scenario, for instance). The rationale for choosing this particular bioeconomic framework is its complex nonlinear structure of (FPBVPs). This complexity is more pronounced than in several other economic models, such as those involving strategic marketing decisions like in Sorger [26]. Such complexity provides a robust test for the JPA’s precision and computational efficiency. We define the temporal evolution of the shared renewable resource’s population within the time span
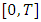 via the subsequent state dynamic and initial state expression [27]:
via the subsequent state dynamic and initial state expression [27]:
 where the smooth function
where the smooth function 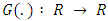 signifies the resource’s intrinsic proliferation rate, taking the logistic growth form as
signifies the resource’s intrinsic proliferation rate, taking the logistic growth form as  with r embodying the intrinsic proliferation rate and k the environment’s carrying threshold. Here,
with r embodying the intrinsic proliferation rate and k the environment’s carrying threshold. Here, 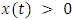 is the population magnitude of the resource at any time
is the population magnitude of the resource at any time  , while
, while 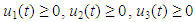 and
and 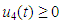 represent the respective harvesting efforts of the enterprises at any given time
represent the respective harvesting efforts of the enterprises at any given time 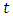 , and
, and 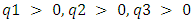 and
and  are the catch efficiency parameters. For any enterprise
are the catch efficiency parameters. For any enterprise  from the set {1, 2, 3, 4}, the cumulative benefit throughout the interval
from the set {1, 2, 3, 4}, the cumulative benefit throughout the interval  is stated a
is stated a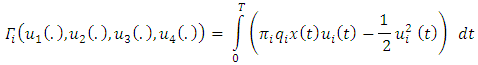 where
where 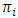 denotes the per-unit revenue from the resource for the
denotes the per-unit revenue from the resource for the 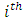 firm. The term
firm. The term 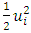 is indicative of the cost incurred due to harvesting at the effort
is indicative of the cost incurred due to harvesting at the effort 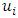 [27].To deduce the Nash equilibria for the companies in this ecological-economic interaction, the Hamiltonian for each firm is formulated as:
[27].To deduce the Nash equilibria for the companies in this ecological-economic interaction, the Hamiltonian for each firm is formulated as: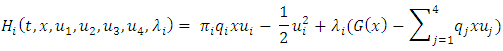 Minimizing
Minimizing 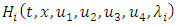 with respect to
with respect to 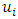 gives the (OLNE) for each entity
gives the (OLNE) for each entity  as:
as: | (30) |
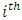 agent is given by:
agent is given by: | (31) |
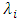 . The FPBVPs for this differential game are characterized by a series of equations corresponding to state, control, and adjoint variables for every firm
. The FPBVPs for this differential game are characterized by a series of equations corresponding to state, control, and adjoint variables for every firm 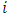 . Assume that the state equation’s unique trajectory, respecting the initial condition, is signified by
. Assume that the state equation’s unique trajectory, respecting the initial condition, is signified by  , and the unique solutions of the adjoint dynamics conforming to the terminal conditions are
, and the unique solutions of the adjoint dynamics conforming to the terminal conditions are 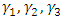 , and
, and 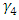 , each pertaining to an individual competitor. According to the ensuing theorem, these conditions uniquely describe the (OLNE) for the quartet of players in the presented bioeconomic game.
, each pertaining to an individual competitor. According to the ensuing theorem, these conditions uniquely describe the (OLNE) for the quartet of players in the presented bioeconomic game. 4.1. Theorem
- The exclusive (OLNE) for the described differential game is uniquely determined by
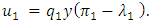 | (32) |
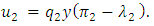 | (33) |
 | (34) |
 | (35) |
 , where
, where 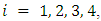 we consider the following optimal control formulations:• For competitor 1:
we consider the following optimal control formulations:• For competitor 1: under the constraint:
under the constraint: 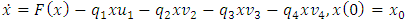 • For competitor 2:
• For competitor 2: 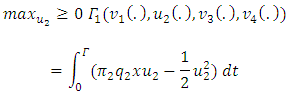 with the boundary condition:
with the boundary condition: 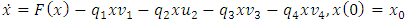
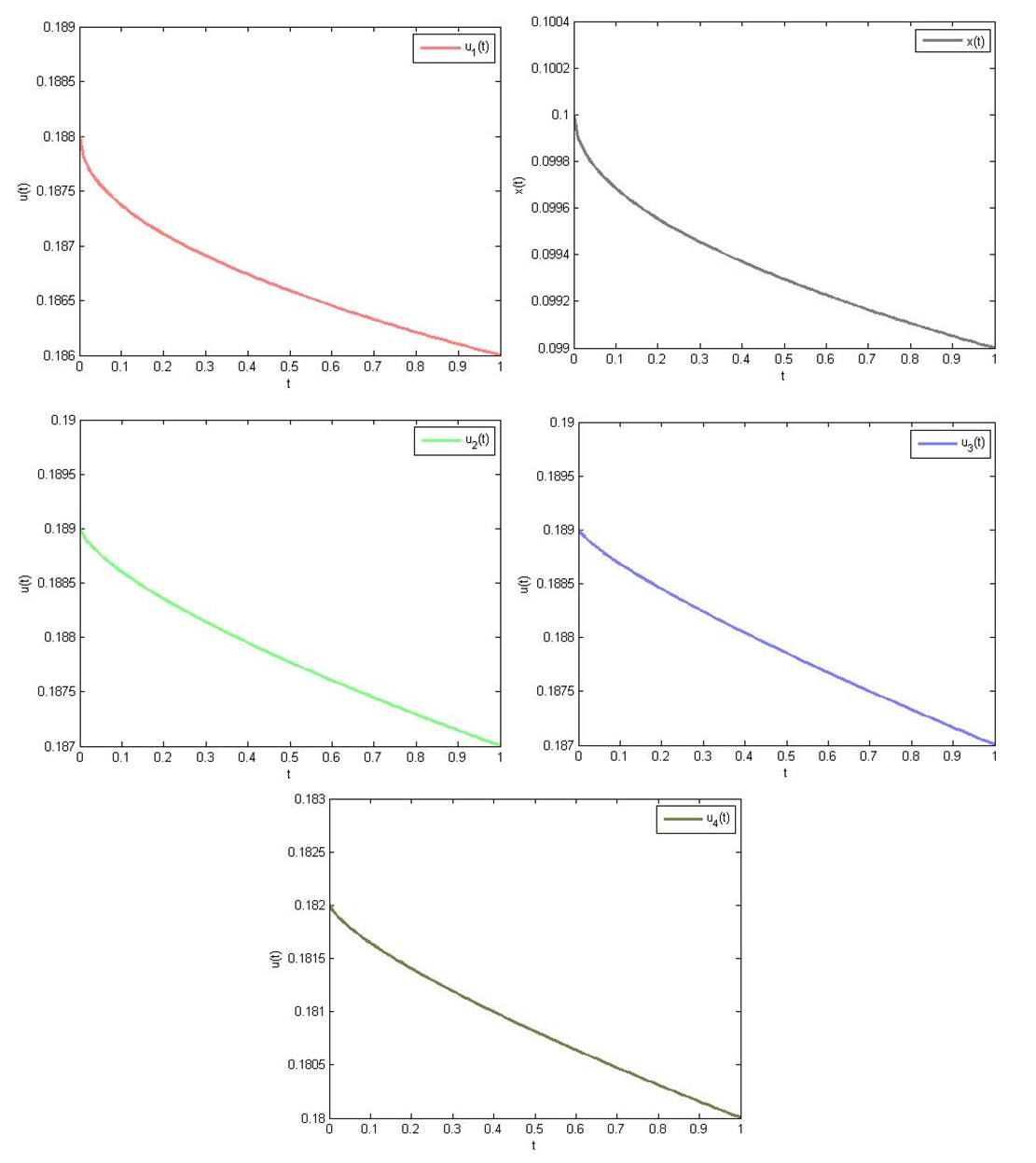 | Figure 1. Plots of approximate (OLNE) for exemplary demonstration when N = 14 |
- The behavior and constraints for competitors 3 and 4 follow suit. For each participant
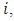 the integrand of the performance measure
the integrand of the performance measure 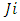 demonstrates concavity as a function of
demonstrates concavity as a function of  indicated by:
indicated by: 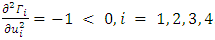 . The remaining part of the proof would similarly address the calculations for the other competitors [28]. The system of FPBVPs constitutes a series of nonlinear differential equations with segmented boundary conditions which usually do not permit an analytical solution. The parameters for a standard scenario are provided as:
. The remaining part of the proof would similarly address the calculations for the other competitors [28]. The system of FPBVPs constitutes a series of nonlinear differential equations with segmented boundary conditions which usually do not permit an analytical solution. The parameters for a standard scenario are provided as: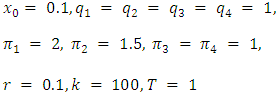 This system of FPBVPs also incorporates the equations for
This system of FPBVPs also incorporates the equations for  and
and 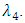 To resolve these FPBVPs, we consider approximations for
To resolve these FPBVPs, we consider approximations for 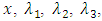 and
and 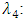
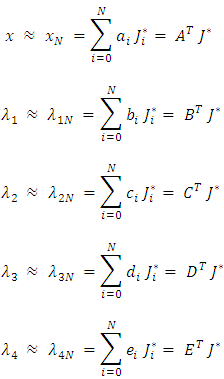 In this approximation,
In this approximation, 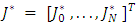 represents the column vector of shifted Jacobi Polynomials. For
represents the column vector of shifted Jacobi Polynomials. For  , representing the differential equation of
, representing the differential equation of 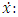
 For
For 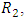 expressing the dynamics of
expressing the dynamics of 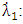
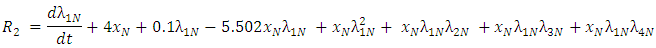 For
For 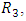 depicting the evolution of
depicting the evolution of 
 For
For 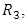 which constitutes the differential equation for
which constitutes the differential equation for 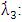
 wherein
wherein  and
and 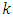 are specific constants akin to those in preceding formulae. For
are specific constants akin to those in preceding formulae. For  the differential equation for
the differential equation for 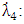
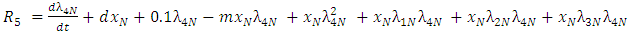 where
where 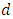 and
and 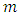 are constants, consistent with the framework of earlier equations.The numerical outcomes for the optimal payoff functions
are constants, consistent with the framework of earlier equations.The numerical outcomes for the optimal payoff functions  , and
, and 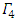 with varying
with varying 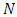 values are presented in the following tables. The graphs of approximate solutions for (OLNE) for
values are presented in the following tables. The graphs of approximate solutions for (OLNE) for  are given in Figure (1).
are given in Figure (1).
|
5. Conclusions
- This research marks a significant stride in the field of economic game theory and computational economics by introducing an efficient algorithmic approach through the (JTM) method. By demonstrating the JTM’s capability to solve complex differential games more accurately than traditional methods, this paper contributes to the precision of economic forecasts and decision-making processes. The implications of these findings have the potential to refine economic models, optimize market strategies, and improve regulatory policies. Looking ahead, the application of JTM could catalyze advancements in financial engineering, market analysis, and resource management, shaping the future of economic theory and practice.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML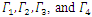 for the four-player illustration with JTM
for the four-player illustration with JTM