1. Introduction

In cooperative games, the most difficult economic problem is to identify how the gains from cooperation should be shared. A pioneering study that addresses this issue is that of Shapley (1953). He considers a cooperative game in characteristic function form and proposes a solution designed to distribute fairly the gains of the coalition of players. This result has many applications, particularly in economics, as well as in social and political science. Remarkably, Shapley proved that the proposed value is the unique value which satisfies four axioms. The first (Efficiency) says that players share among them the resources available to the grand coalition. The second (Additivity) requires that the value be additive on the space of all games. The third (Symmetry) requires that players who make the same marginal contribution to any coalition should have the same value. The last (Null player) requires that players who have zero marginal contribution to any coalition must have zero payoffs.

The Null Player axiom, stating that "players who make no marginal contribution in any coalition must have zero payoffs", is challenging because, for the survival of a group, it is necessary that some transfer of the gains is made to any such player.

The solidarity value was first introduced by Sprumont (1990). In the solidarity value the individual marginal contribution is replaced by the average of the marginal contributions of all players belonging to a coalition. Nowak and Radzik (1994) characterize this value axiomatically by means of the same axioms as those found used for the Shapley value but replacing the null player axiom by the A-null player axiom (A-null stands for average null). A player receives zero if the average of the marginal contributions is across all coalitions to which he (she) belongs. Nowak and Radzik (1994) have proposed a new solution for cooperative TU games which they entitle "the solidarity value". If a player wants to join a coalition, he will receive a fraction of the benefits which depends on the average contribution of players in this coalition. If the marginal contribution of the player is higher than the average contribution of the coalition, he will offer a part of his contribution to the coalition. This has positive effects on players whose marginal contribution does not reach the level of the average contribution of the coalition.

In the solidarity solutions proposed in literature by Nowak and Radzik (1994) it is assumed that, in a coalition, all players with a marginal contribution higher than the average contribution of the coalitions must exhibit solidarity towards the others. This can lead to situations where the poor (a player with small marginal contributions) can, through transfers, achieve a more favorable status, and sometimes can attain a social level near to the productive players.

To summarize, the Shapley value does not allow for solidarity, so that unproductive player gains zero payoff. The equal division value divides the surplus equally among the players (extreme kind of solidarity). The principle of solidarity conceived in this work, can be made between Shapley value and Solidarity value: the player decides to give, with his consent, and without expecting the slightest compensation for his contribution. Each player can give a fraction of his own payoff and favor one or several players without disadvantaging other players in the game. For more literature on solidarity value, we can see Calvo and al. (2013), Lambo and al. (2015), Béal and al. (2017), Hu and al. (2018), Nléndoum and al. (2020) and Zou and al. (2023).

The aim of the paper is to identify how the gains in a cooperative game should be shared in the presence of a solidary players (forming a coalition 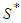) and non-solidary players. The new value is denoted by 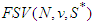. The rest of this paper is organized as follows. Section 2 is devoted to basic definitions. Section 3 introduces the free solidarity value. We provide the axiomatic characterization of this value in Section 4. The conclusions are presented in Section 5. The proofs are stated in an appendix (section 6).

2. The Shapley Value, the Solidarity Value

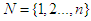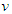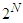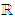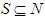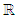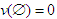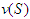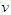We consider a coalitional form game with transferable utility (every coalition can divide its worth in any possible way among its members) on a finite set of players . Such a game is designated by a function from the set of all coalitions to , and assigns to each coalition a real value in with . The real represents the total payoff or rent the coalition can get in the game and it is considered as a monetary value (players having similar preferences) in the case of cooperative TU-games. In most interesting economic applications, the function 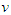is super-additive, so that it is efficient for the players to form the grand coalition, 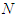. The question then arises of how to divide .

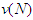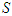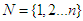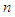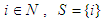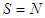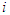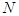A coalition is a subset of the set of players. For is a coalition of one player (singleton), is a coalition of all the players in the game (grand coalition), for simplicity we use and for the singleton coalition and for the grand coalition. For any coalition 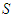or 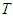, let us denote by 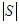(respectively 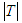) the cardinal (the number of players) of 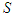(respectively of 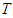). We also use

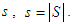For a game 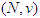, to divide 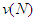we use a value function. A value function 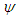which associates to each player 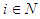a real number 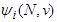which represents the payoff of player 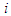when he participates in the game 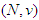. Let denote by 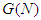the space of coalitional form games with transferable utility and 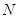the fixed set of players.

The famous Shapley Value assigns an expected marginal contribution to each player in the game with respect to a uniform distribution over the set of all permutations on the set of players. Shapley proved that the proposed value is the unique value which satisfies four acceptable axioms. The first (Efficiency) says that players distribute among themselves the resources available to the grand coalition. The second (Additivity) requires that the value be additive on the space 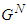. The third (Symmetry) requires that players who make the same marginal contribution to any coalition, have the same value. The last (Null player) requires that players whose marginal contribution is null with respect to every coalition must have zero payoffs.

The Shapley Value depends on the marginal contribution of player in all the coalitions he can join. Let 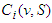be the marginal contribution of player 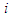in the coalition 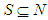in the game 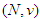. This contribution can be formally defined as follows:

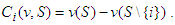The Shapley Value 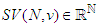is given by:

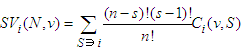(1)

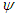Theorem 1 [Shapley 1953] A value on 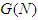satisfies Efficiency, Additivity, Symmetry and the Null player axiom, if and only if 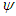is the Shapley Value, i.e.,

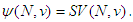Nowak and Radzik (1994) have proposed a value named the Solidarity Value. This new value attributes to any player 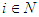the average marginal contribution of all players in the same coalition 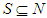. Let 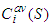be the average contribution of coalition 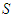containing a particular player 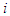in the game 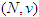. In this case, all the players forming 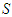have 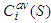as their contribution.

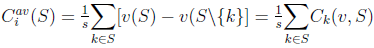The Solidarity Value (NRV) of a TU-game 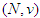is given by: for each ,

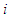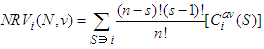(2)

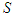The (NRV) is computed like the Shapley value but replacing the marginal contribution of a player by the average marginal contribution. Compared to Shapley (1953), the only new axiom introduced by Nowak and Radzik (1994) is the A-Null Player Axiom: if it happens that every coalition containing player 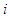has a null average contribution then player 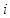gets nothing from the game .

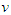A-Null Player: If 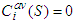for every coalition 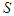containing 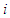, then 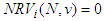. Player 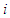is said to be an A-null player. There is clearly no relation between the null player and the A-null player concepts.

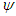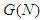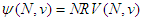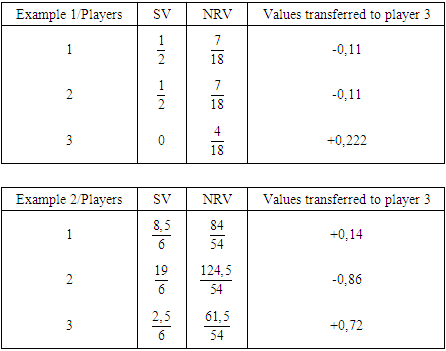
Theorem 2 [Nowak and Radzik 1994] A value on , satisfies the Efficiency, Additivity, Symmetry and A-Null player axioms if and only if , i.e., 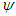is the solidarity value.

Let us consider some examples through which we compute the (SV), (NR) values and the amount of the transfer from rich players to poor players.

Example 1 (Three Brothers):¹

Players 1, 2 and 3 are brothers and they live together. Players 1 and 2 together can make a profit of one unit, that is, 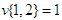. Player 3 is a disabled person and can contribute nothing to any coalition. Therefore, 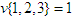. Furthermore, we have 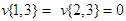. Finally, we assume that 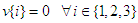for every player 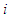. This is a classical unanimity game. The Shapley value of the game is 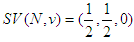. If players 1 and 2 take responsibility for their brother (player 3), then the solidarity value .

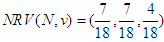Example 2: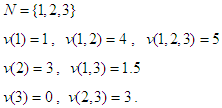

Remark

As it is cited in Nowak and Radzik (page 44) the solidarity values works as follow: If a player 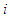joins a coalition 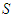and if its marginal contribution is greater than the average marginal contribution, player 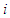offers some part of his/her marginal contribution to the coalition 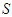to support one or more weaker members of 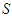. Now if for some player 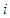, the marginal contribution is smaller than the average marginal contribution, then player 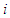benefits from joining coalition 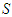. So, for a given player say 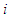when varying the coalition 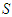containing the player 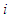, it happened that player 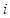benefits from the fact that he (or she) has been accepted to became a new member of a coalition 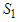, and not when he (or she) became member of another coalition 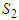. For example 1, players 1 and 2 transfer 0,222 of their values to the null player 3. In example 2, player 3 is not a null player, and he receives 0,72 and has a value near to player 1's value. Initially, player 1 has three times the value of player 3, player 1 receives 0,14 from player 2. It is clear that solidarity in example 2 is supported only by player 2. Initially (with Shapely value) the player 1 has 28,33% of the total amount (here=5), while player 2 has 63,33% and player 3 has 8,33%. With the solidarity value, the value of player 1 increases to 31,11%, the value of player 2 decreases to 46,11% and the value of player 3 increases to 22,77%. Why player 1 should benefit from solidarity?. The solidarity value can lead to situations where through transfers the unproductive players can achieve a more favorable status, and the productive players can also benefit. The solidarity is supported only by higher productive players. From example 2, it is strategic for player 1 to be solidary player, as it is shown he (or she) benefits from solidarity. In the next section we present a method for a possible formation of a coalition containing the unproductive players and one or more player productive accepting to be solidary player under the condition that they did not accept that a productive player will profit from the solidarity that they did.

3. The Free Solidarity Value

Let us now suppose that some players decide to be solidary and others not solidary. Thus we have two types of players: solidary and not-solidary players. As we have seen in example 2 some players strategically can benefit from solidarity. We denote this coalition grouping of solidary players and unproductive players by 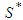. Among solidary players, each will have 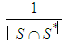of the sum of their marginal contributions every time they find themselves in the same coalition .

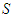When the coalition is mixed, formed by both types of players, and to reflect a certain social behavior of the players in a game, we define the following two types of contributions:

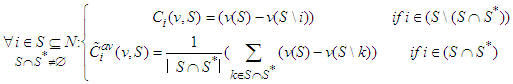Every non-solidary player 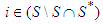will have a value depending on its marginal contribution 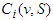, and every solidary player 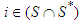will have a value according to its average marginal contribution .

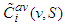Note that, contrary to the seminal paper of Nowak and Radzik (1994), the average marginal contribution 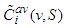that we propose through the last formula may be partial, if the players of the same coalition are not all solidary.

The Free solidarity value 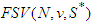of a cooperative TU-game 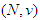is given by:

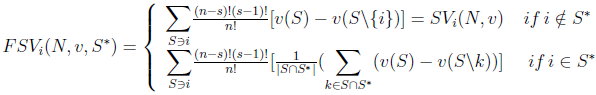(3)

We present a method of the formation of a coalition containing the unproductive players and one or more productive players accepting to be solidary players under the condition that they will did not accept that one or more productive players will profit from the solidarity that they did. If the case occurs they refuse to be solidarity players.

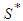A possible formation of : We assume that players are ordered as:

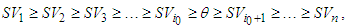Where 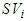is the Shapley value of player 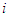and 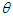is some exogenous value separating the players into two coalitions: the productive players and the unproductive (or with weak production) players.

1. 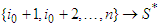. The unproductive players initially form the coalition .

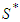2. Productive players can accept to be solidary or not. Respecting the order of the productive players in 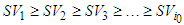. Let 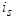be the first player accepting to be solidary, 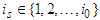. Then 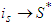. The coalition 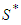contains the player .

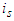3. If some player 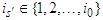with 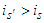joins the coalition 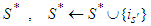. The grand coalition 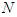is partitioned into 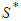and 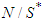. At this state the values of players can be given by 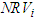for players in 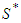and 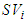for players in 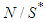. If player 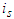observes that 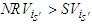, player 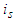leaves the coalition 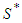and 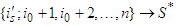. The solidarity is supported only by player 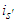. Now if 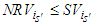, and if 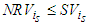, then .

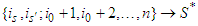4. And so on.

This procedure can give two solutions:

1. 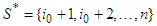. Which means that the solidarity players do not exist. In this case we assume 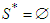and players divide the value following Shapley value.

2. 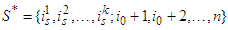, where 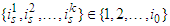are productive and solidary players.

Let compute the FSV for examples 1 and 2.

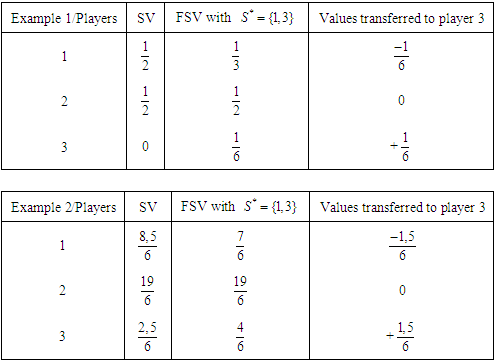Here the transfer from player 1 to player 3 is 0,16 for example 1, and 0,25 for example 2.

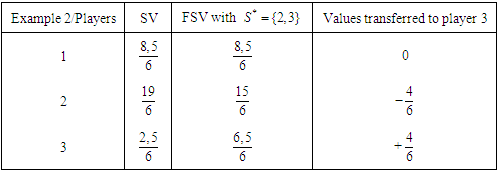Here player 2 transfers 0,66 of his value to player 3.

Remarks

1. According to the Shapley value, the players behave in an individual way. Every player will have a value which depends only on its own marginal contribution in the coalitions which it can form. They are not obliged to help their weaker partners.

2. With the Solidarity Value, all the players who make a contribution to the coalitions which is greater than the average marginal contribution should support their weaker partners. As we have seen some productive players can benefit from solidarity.

3. With the free solidarity value, the not-solidarity player is not punished because he does not agree to help any body, and therefore he is going to be able to control his acts of solidarity to remain at least as satisfied as possible. Following the procedure of the formation of , the possible coalitions in examples 1 and 2 are given by: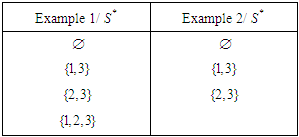

4. An Axiomatic Characterization

Let given the space 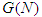of coalitional form games with transferable utility and 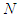the fixed set of players. Let 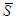and 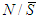a partition of the grand coalition, such a partition is called a 2-partitions of 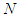(we assume that 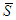can be empty). It is assumed that if players are grouped in a given 2-partition of 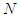, this should not affect the characteristic function 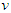, for each 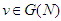. For each 2-partition of 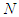, 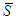and 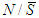and for each game 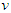, let 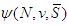be the value of players in 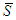and let 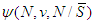the value of players in .

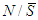Axiom A(1), Efficiency (Eff): For any 2-partition of 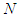, 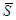and 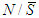and for any game ;

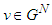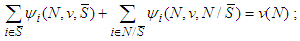Axiom A(2), Additivity (Add): For any 2-partitions of 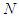, 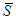and 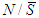and for any game ;

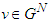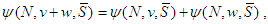
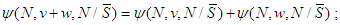Axiom (A3), Unaffected Allocation - UA): For any 2-partitions of 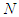, 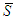and 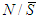and for any game ;

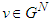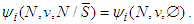The value of the players in 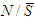is the same than the value when all players are regrouping in the grand coalition. We can define the unaffected allocation differently by saying: when players form 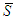this should not affect the values of the other players who are stay out;

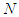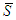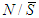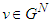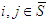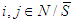Axiom A(4), Conditional Symmetry (Cond Sym): For any 2-partitions of , and and for any game ; Players i,j are said to be conditionally symmetric, if or and .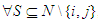

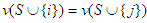Conditionally symmetric players i,j have the same value, ;

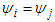Axiom A(5): (Conditional Null player: Cond-null player): For any 2-partitions of 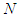, 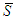and 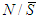and for any game 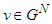; A player 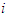is said to be a Cond-null player if, (1) 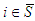and the average marginal contribution is null when 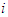joins any coalition, or (2) 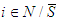and the marginal contribution is null when 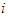joins any coalition.

If a player 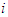is conditional Null player then his or here value is zero, that is .

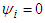Axiom A(3) is new, and it means that for every 2-partitions of 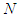, the values of players in 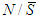are not affected by the partition. The 2-partitions affects juste the values of players in .

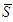Axioms A(1)--A(2) are standard.

Axiom A(4): As we have two types of players: those belonging to 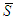and those belonging to 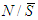. One cannot compare two players of different types according to their marginal contributions. It is for this reason that we supposed a comparison according to their membership. If it happens that in every coalition 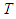containing two players of the same type, they make the same marginal contributions, then they should be rewarded equally.

Axiom A(5) can be seen as a combination of the Null Player Axiom of Shapley (1953) and the A-null Player Axiom of Nowak and Radzik (1994).

For a given player 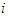, the two and only two possible cases are, 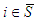or 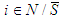. (1) If 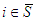and if for every coalition 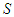containing player 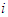has a null average contribution; or (2) if 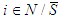if for every coalition 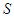containing player 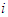has a null marginal contribution. Axiom A(5) says that the player 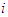in this two distinct cases must receive zero.

The following is the main results of the paper, the proofs are done in the appendix.

Theorem 1:

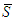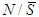Let a 2-partitions and of 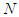. A value 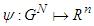satisfies Efficiency, Conditional Symmetry, Additivity, Unaffected Allocation of Non-Solidary Players and a Conditional Null Player axiom for each game 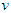if and only if

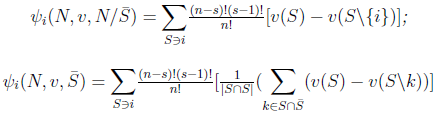Corollary 1:

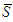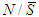Let a 2-partitions and of 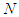such that 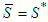. Assume that the axioms of Theorem 1 are satisfied each 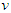. Then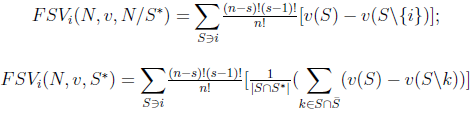

5. Discussion and Concluding Remarks

A cooperative games with transferable utilities with possibly two types of players is studied, players in 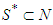willingly share their payoffs with themselves to a certain extent even though some of them are unproductive (i.e., they have principles of solidarity), and the others (those in 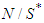) do not. These differences among players are endogenous, thus each

player cannot strategically choose which group he or she belongs to. A principle of solidarity has already discussed in literature on solutions for usual TU games. Nowak and Radzik (1994) introduce players average marginal contributions to each coalition and define the solidarity value, which is an expectation of each player's average marginal contributions. This value has a clear contrast with the well-known Shapley value (Shapley 1953), which is an expectation of each player's marginal contributions. The solidarity value represents a situation where all players have principles of solidarity, and hence players in a coalition completely share one's marginal contributions to the coalition among them, while the Shapley value (Shapley 1953) represents a situation where no one has principles of solidarity. These two existing values study only extreme cases: all players have the principle of solidarity or not.

The proposed value in this paper is an intermediate situation between the solidarity value and the Shapley value by dividing players into two groups in advance. The main contribution is an axiomatic characterization of the free solidarity value. Given a game 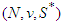, the free solidarity value assigns the solidarity value-like payoffs for players in 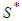(these players completely share one's marginal contributions to the existing players who are in the same type), and the Shapely value payoffs for players in 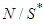. This value is characterized by five axioms of A(1) efficiency, A(2) additivity, A(3) unaffected allocation of non-solidarity players, A(4) conditional symmetry, and A(5) conditional null player. This characterization is in parallel with those of the Shapley value and the solidarity value, each of which is characterized by efficiency (corresponding to A(1)), additivity (to A(2)), symmetry (to A(4)), and a null player (resp. A-null player) axiom (to A(5)). The proof is not trivial and the axiom A(3) plays a critical role for distinguishing result from existing ones, and this axiom requires that redistributions among solidarity players do not affect the payoffs for non-solidarity players. We have also looked to a possible formation of 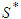under the condition that solidarity cannot be benefit to productive players. As it can be seen from example 2, the solidarity (NR) is supported only by the higher productive player (player 2), can this be true in general is an open question.

6. Appendix: Proof of Theorem 3

For the proof of the Theorem 3, let first look to the unanimity game 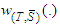expressed in the following definition. It is shown that the values of a unanimity game satisfying the axioms are uniquely defined. Each game can be expressed as a linear combination of unanimity games. We then deduce that the value is unique. The last point of the proof consists in showing that the analytical given value FSV satisfies the axioms. The set of solidarity players is assumed non empty. However, in the definition of the unanimity game given below, we consider the two cases when solidarity set exists (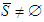) and when no solidarity set exists (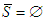).² For the proof we follow the same steps as Nowak and Razik (1994). To be precise, we will divide the proof as some Lemmas, in which the proof uses one or moore axioms.

Definition: (Unanimity Game)

Let 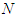be a set of 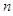agents and 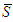the coalition of solidary players. For 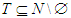, the unanimity games 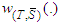are such that}

1. If the coalition of solidary players 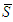is not empty.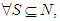

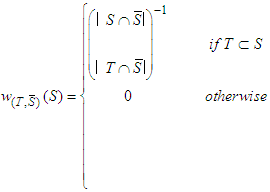(4)

Where .

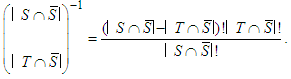2. If the coalition of solidary players is empty.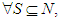

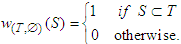(5)

Lemma 1

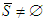Let assume that . the game has the following properties:

1. If 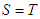, then

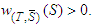2. If with ,

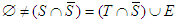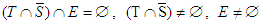then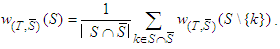

Proof:

1. W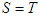hen then,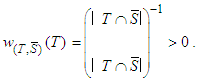

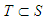2. If with 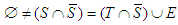, ,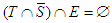, ,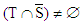 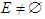then

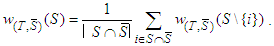Using the expression for 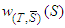in (4), we have:

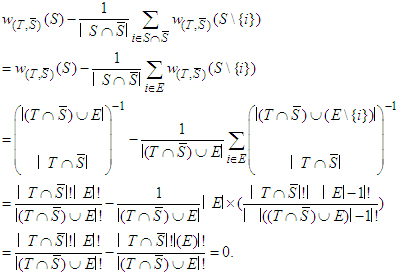(6)

Lemma 2:

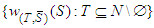The set is a linear basis for .

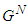Proof: Follows from Nowak and Radzik (1994).

Lemma 3:

Whatever its type, any player who is not in T is a Cond-null player in the game 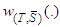, i.e., the marginal contribution (when 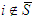) or the average marginal contribution (when 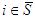) of a player is equal to 0, and thus by A5, ,

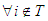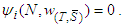Proof: Let consider the case

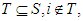• If 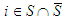. Let write

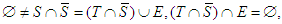Then 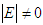, otherwise 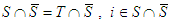and 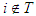(which is a contradiction).

From Lemma 1,

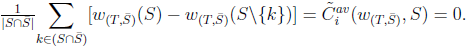• If .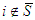

It's clear that 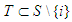since 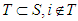, and 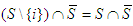. Then 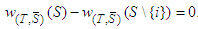So, 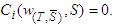Thus by A(5) we can say that, 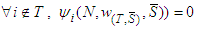i.e., it is a Cond-null player.

Lemma 4:

Every two players i, j of the same type in 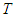are conditionally symmetric in the game 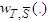. From Cond Sym axiom i, j have the same value.

Proof: Let show that for each i,j such that 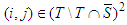or 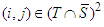we have 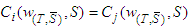, for each coalition 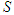containing 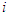and 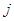. It is obvious from .

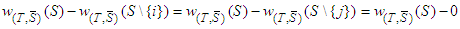Lemma 5:

Assume efficiency, unaffected allocation and conditional symmetry. Then

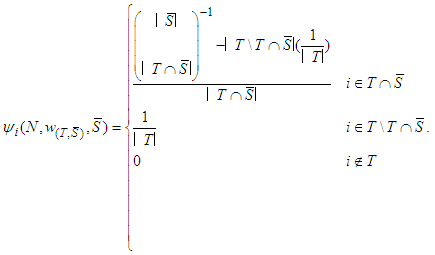Therefore for each constant

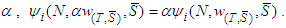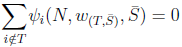Proof: Since is efficient, and (from Lemma 3) then;

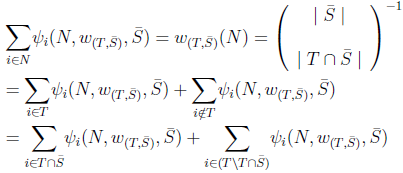From the unaffected allocation of non-solidary players axiom, we have

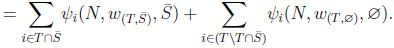Then,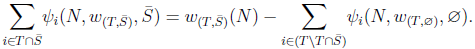

The unanimity games defined by (5) are those used for characterizing Shapley value, it is known that 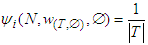for 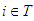(Shapley 1953).

Then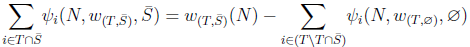

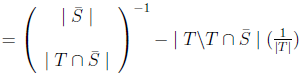1. For any player 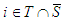will have

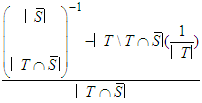2. For any player 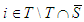will have .

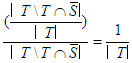3. For any player 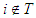will have zero.

Then

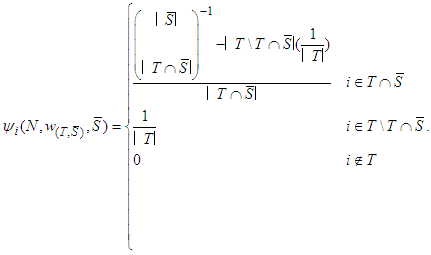Therefore for each constant

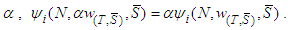Lemma 6:

Assume efficiency, unaffected allocation, conditional symmetry and additivity. Let 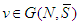, then 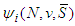is uniquely defined.

Proof: From the previous Lemmas and the additivity axiom,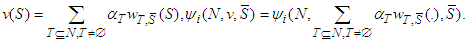

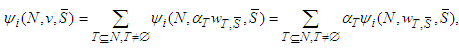
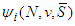is then uniquely defined.

Proof of Theorem 3: From the previous Lemmas it suffice to show the existence of the free solidarity value. Letting 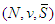be a TU game, we consider our proposed solution, defined by (3). We are going to check whether this allocation satisfies the axioms. The first axiom is trivial.

• Eff:

We know that the Shapley value satisfies Efficiency:

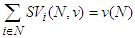but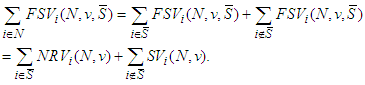

Therefore it suffices to prove that

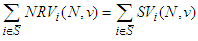Otherwise it suffices to prove that

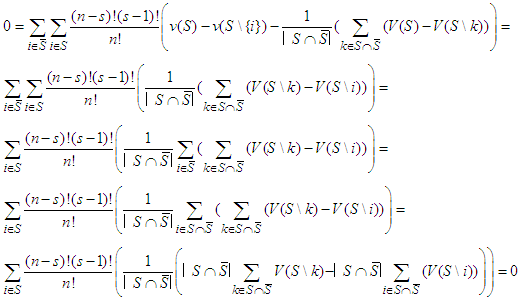Which proves that is an efficient value.

• Cond-null: Let be a Cond-null player:

1. If , i.e.,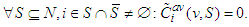

So in this case, .

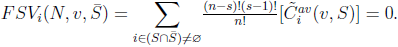2. If 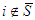, i.e,

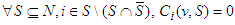So .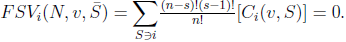

Thus, the free solidarity value satisfies the Cond-null Axiom when 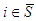or when .

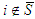• Cond Sym: Let 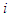and 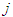be conditionally symmetric players:

By A(4), for all 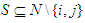we have

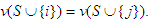1. if :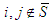

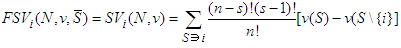Which can be written 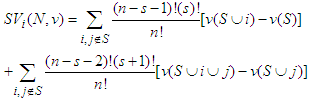as:

As 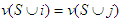for each coalition 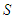not containing 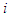and 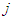, then 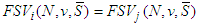; the free solidarity value satisfies Cond Sym when .

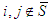2. if 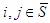we have:

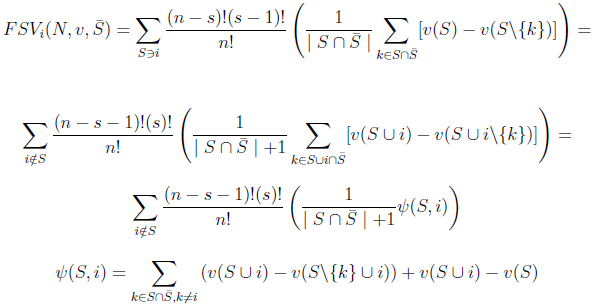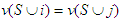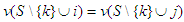Now, as and , then 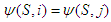. The free solidarity value satisfies Cond Sym when .

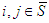• Unaffected Allocation of Non-solidary Players

For a game 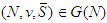, for all 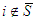, we have:

• Add: FSV is linear, so Add is satisfied.

Note

*This paper is a revisited version of the working paper: Free Solidarity Value, 2015, University of Caen Basse Normandie, Center of research in Economics and Management (CREM, UMR CNRS 6211).

1. Nowak and Radzik [1994].

2. 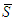contains some productive players and the unproductive players. When 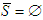, then no productive players accept to be solidary.