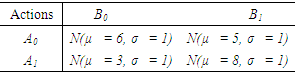-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2022; 11(1): 1-5
doi:10.5923/j.jgt.20221101.01
Received: Jul. 28, 2022; Accepted: Dec. 5, 2022; Published: Dec. 23, 2022

Equilibrium in Multi-stage Game Playing with Dynamic Programming
Beidi Qiang
Southern Illinois University Edwardsville, Edwardsville, IL, USA
Correspondence to: Beidi Qiang, Southern Illinois University Edwardsville, Edwardsville, IL, USA.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the problem of multi-stage game playing is studied in a decision theory framework. The conditional strategies of payers are examined under the assumption of perfect information about previously played stages. The equilibrium is defined in analogy to the Nash equilibrium and the existence of such equilibrium is discussed mathematically through the idea of dynamic programming and backward induction. An example in a two-players zero-sum game setting is analyzed with details and the solution of the equilibrium strategy is presented.
Keywords: Multi-stage game, Dynamic game, Nash equilibrium, Dynamic programming
Cite this paper: Beidi Qiang, Equilibrium in Multi-stage Game Playing with Dynamic Programming, Journal of Game Theory, Vol. 11 No. 1, 2022, pp. 1-5. doi: 10.5923/j.jgt.20221101.01.
Article Outline
1. Introduction
- In game theory, Nash equilibrium is one of the most well-studied solutions to a single-stage non-cooperative game. An equilibrium in the game is defined as no player can do better by unilaterally changing his strategy. It is proved that if mixed strategies are allowed, then a game with a finite number of players and finitely many pure strategies has at least one Nash equilibrium [1]. The problem of finding equilibrium in various single-stage game settings has been studied in the literature. In reality, dynamic game playing over time is more complex than one game. Instead, decision-makers are expected to play one game followed by another, or maybe several other games. It is tempting to view each game independently and assume players do not make any attempt to link them. If each player treats every game independently, equilibrium can be studied for each of the stage games in turn. However, this approach ignores any real issues concerning sequential behavior, if we consider the games played sequentially as stages of a larger game and players can observe the outcomes of each game before another game is played. If players are rational and forward-looking, they should view the sequence of decision-making as part of one large game. And if they do, we expect their actions to be dependent on the outcome of the previous games. The existence and solutions of equilibrium for dynamic games are well-studied in the literature. The existence of sub-game equilibria in simultaneous move games with finite actions was discussed by Fudenberg and Levine 1983 [2]. Kreps and Wilson [3] proposed the concept of sequential equilibrium and Myerson [4], in his key paper in 1986, discussed the sequential communication equilibrium in multi-stage games with communication mechanisms that can be implemented by a central mediator. There has been a surge of discussions in multistage game playing with various designs of dynamic mechanisms and information systems. For example, Renault, Solan, and Vieille [5] studied a dynamic model of information provision with a greedy disclosure policy, and He and Sun [6] discussed the existence of subgame-perfect equilibria in dynamic games with simultaneous moves.In this paper, we discuss details of conditional decision-making in a multi-stage game with players choosing their actions simultaneously at each stage. Games at each stage are played sequentially, with actions and information from previous games unfolding, but the payoffs were delayed until the sequence ends. These games form a general class of dynamic games with many applications in economics and political science. We define the settings of a multi-stage game and its equilibrium in section 2. The existence of equilibrium in this game setting is discussed through the idea of backward induction in section 3. An example of a simple game with two players and two stages is presented in section 4. Concluding remarks are discussed in section 5.
2. The Setting of a Multi-Stage Game
- Consider a multi-stage game with
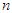 players and finite
players and finite 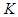 stages. At each stage, player
stages. At each stage, player 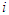 , has a finite strategy space
, has a finite strategy space 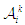 . Let
. Let 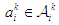 denote the pure strategy chosen by player
denote the pure strategy chosen by player 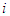 at stage
at stage 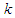 . Then
. Then 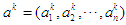 is the profile of strategies used by each player at stage
is the profile of strategies used by each player at stage 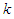 , where
, where 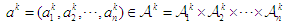 . Assume the game at each stage is a simultaneous move game, i.e a normal-form game. At stage
. Assume the game at each stage is a simultaneous move game, i.e a normal-form game. At stage 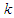 , the outcome for player
, the outcome for player 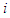 is denoted by
is denoted by 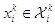 and the combined outcome for all players is denoted by vector
and the combined outcome for all players is denoted by vector 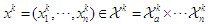 . Assume the combined outcome at stage
. Assume the combined outcome at stage 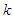 comes from a joint distribution that is known given the joint choice of actions, i.e.
comes from a joint distribution that is known given the joint choice of actions, i.e. 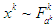 , where
, where 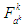 depends on the joint action
depends on the joint action 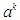 . Assume each game is played in a distinct period and also that after each stage is completed, all players observe the outcome of that stage and all outcomes gained before that stage, i.e.
. Assume each game is played in a distinct period and also that after each stage is completed, all players observe the outcome of that stage and all outcomes gained before that stage, i.e. 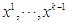 are observed for each player at stage
are observed for each player at stage 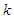 . It is plausible that the action of each player at stage
. It is plausible that the action of each player at stage 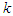 will depend on the observed outcome at previous stages. In this setting, the outcomes of previous stages become common knowledge, and players are allowed to make conditional strategies for future games based on past outcomes.
will depend on the observed outcome at previous stages. In this setting, the outcomes of previous stages become common knowledge, and players are allowed to make conditional strategies for future games based on past outcomes. 2.1. The Payoff
- The games are played sequentially, and the total payoffs from the sequence of games will be evaluated using the sequence of outcomes at the end of the games, i.e. after stage
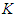 . Suppose each player receives a real number payoff or reward. The reward function
. Suppose each player receives a real number payoff or reward. The reward function 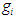 for player
for player 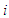 is defined as a function of the outcomes of all
is defined as a function of the outcomes of all 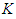 stages, i.e.
stages, i.e. 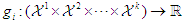 . The joint reward function for all players is then defined as
. The joint reward function for all players is then defined as 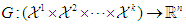 , where
, where 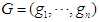 . With the reward function defined, the expected reward of each player can be calculated when the joint strategies at all stages are given. Given the joint actions at all stages
. With the reward function defined, the expected reward of each player can be calculated when the joint strategies at all stages are given. Given the joint actions at all stages 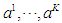 , the expected reward for player
, the expected reward for player 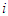 is defined as
is defined as 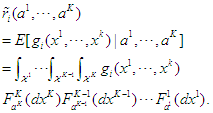
2.2. Mixed Strategy
- In a general setting, at a given stage, each player is allowed to have mixed strategy, i.e. players choose actions based on a probability distribution of possible pure strategies at the stage. Consider the decision function for player
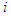 at stage
at stage 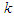 ,
, 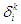 , as a function from the product space of the previous outcome space
, as a function from the product space of the previous outcome space 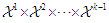 to the probability space of strategies at stage
to the probability space of strategies at stage 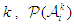 . And the joint decision function for all players at stage
. And the joint decision function for all players at stage 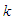 is then denoted by
is then denoted by 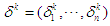 , where
, where 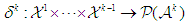 .Assume the joint reward
.Assume the joint reward 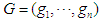 at the end of the game is defined the same as above. Given the joint mixed strategies at all stages,
at the end of the game is defined the same as above. Given the joint mixed strategies at all stages, 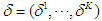 , the expected reward for player
, the expected reward for player 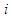 is can be calculated as
is can be calculated as 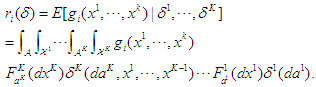
2.3. Definition of Equilibrium
- In a single-stage game, the Nash equilibrium is achieved when no player can increase his own expected payoff by switching his strategy. A collection of mixed strategies for all players,
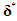 , is considered to be the equilibrium strategies if for all
, is considered to be the equilibrium strategies if for all 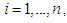 ,
, 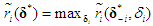 where
where 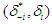 denotes a new set of mixed strategies when only player
denotes a new set of mixed strategies when only player 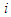 switched from mixed strategy
switched from mixed strategy 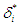 to
to  . Due to the multi-stage nature of the game, the decisions for all players are made stage by stage based on the previously observed outcomes. The equilibrium joint strategies of the game is thus defined sequentially as no players can be better off by switching to another strategy at each stage conditionally on observed previous outcomes. The joint mixed strategies for all players at all stages
. Due to the multi-stage nature of the game, the decisions for all players are made stage by stage based on the previously observed outcomes. The equilibrium joint strategies of the game is thus defined sequentially as no players can be better off by switching to another strategy at each stage conditionally on observed previous outcomes. The joint mixed strategies for all players at all stages 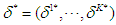 , is considered to be an equilibrium if at any stage
, is considered to be an equilibrium if at any stage 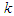 given outcomes from stage 1 to
given outcomes from stage 1 to 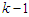 , for all player
, for all player 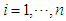 . The expected reward of player
. The expected reward of player 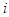 at the equilibrium satisfies the following,
at the equilibrium satisfies the following,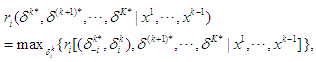 where
where 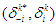 denotes a new joint randomized decision at stage k when only player
denotes a new joint randomized decision at stage k when only player 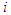 switched from
switched from 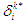 to
to 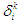 .
. 3. The Existence of Equilibrium
- It has been shown that there is a Nash equilibrium for every single-stage finite game when mixed strategies are allowed. The proof of existence is outlined in Nash's original paper using Kakutani fixed-point theorem [7]. We now extend the discussion to a multi-stage game using the idea of dynamic programming and backward induction, which was developed by Richard E. Bellman [8]. The essence of dynamic programming is to simplify a complicated optimization problem by breaking it down into simpler sub-problems recursively. The nature of a multi-stage game allows us to break the game down into a sequence of sub-games over discrete time, with each sub-game as a finite non-cooperative game. Starting from the end of the game, we first examine the last stage and identify what strategy would be most optimal at that moment. We then backtrack and determine what to do at the second-to-last time the decision. This process continues backward until one has determined a sequence of optimal actions for every possibility at every point. Consider the last stage, stage
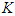 , of the game when the outcomes of the previous stages are observed. The expected reward based on the joint decision of all players at the last stage,
, of the game when the outcomes of the previous stages are observed. The expected reward based on the joint decision of all players at the last stage, 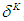 , is given by
, is given by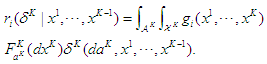 When the outcomes from stage 1 through
When the outcomes from stage 1 through 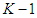 , i.e.
, i.e. 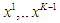 are observed, the game at the last stage becomes a single stage game, which has an equilibrium as proved by Nash [7]. Denote the equilibrium decision at stage
are observed, the game at the last stage becomes a single stage game, which has an equilibrium as proved by Nash [7]. Denote the equilibrium decision at stage 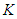 based on previous observations as
based on previous observations as 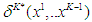 and the equilibrium expected reward given outcomes from stage 1 to
and the equilibrium expected reward given outcomes from stage 1 to 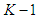 is given by
is given by 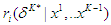 . If the players follow the equilibrium strategy
. If the players follow the equilibrium strategy 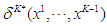 at stage K, then the expected reward can be written as
at stage K, then the expected reward can be written as Assume all players follow joint strategy
Assume all players follow joint strategy  at stage
at stage  , now consider stage
, now consider stage  given the information of previous outcomes up to stage
given the information of previous outcomes up to stage 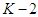 . The expected reward is then given as
. The expected reward is then given as 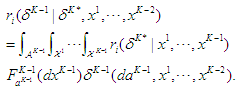 This again becomes a single-stage game, and Nash equilibrium exists. Denote the equilibrium decision at stage
This again becomes a single-stage game, and Nash equilibrium exists. Denote the equilibrium decision at stage 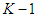 as
as 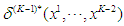 and the equilibrium expected reward given outcomes from stage 1 to
and the equilibrium expected reward given outcomes from stage 1 to 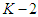 is given by
is given by 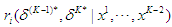 . Repeat the process sequentially for stage
. Repeat the process sequentially for stage 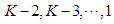 . We can then find an equilibrium decision for all stages,
. We can then find an equilibrium decision for all stages, 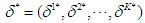 .
.4. An Example
4.1. A Game with 2-Stages
- Consider a simple game with
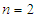 players and
players and 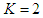 stages. Players are non-cooperative and play simultaneously. Player
stages. Players are non-cooperative and play simultaneously. Player 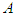 has 2 pure strategies to choose from at each stage, denoted by
has 2 pure strategies to choose from at each stage, denoted by 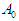 and
and 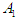 . Similarly, player
. Similarly, player 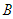 also has 2 possible pure strategies,
also has 2 possible pure strategies, 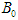 and
and 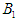 . Assume the outcomes for player A and B are the same at each stage, and follow a distribution
. Assume the outcomes for player A and B are the same at each stage, and follow a distribution 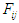 , if player
, if player 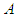 choose pure strategy
choose pure strategy 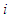 and player
and player 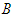 choose pure strategy
choose pure strategy 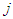 at the stage, i.e.
at the stage, i.e. 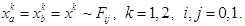 Assume mixed strategies are allowed. Let
Assume mixed strategies are allowed. Let 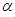 denote the probability of player A choosing pure strategy
denote the probability of player A choosing pure strategy 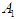 and
and 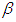 be the probability of player B choosing strategy
be the probability of player B choosing strategy 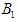 .
. 4.2. The Reward Function
- Consider the zero-sum game, in which the sum of rewards for players
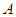 and player
and player 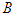 equals zero. Consider the situation that the goal of player
equals zero. Consider the situation that the goal of player 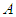 in this game is to reach a threshold
in this game is to reach a threshold 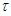 and the opponent
and the opponent 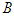 wants the opposite. Furthermore, assume the game stops whenever the threshold
wants the opposite. Furthermore, assume the game stops whenever the threshold 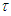 is achieved. Thus, the reward function at the end of the game is given by
is achieved. Thus, the reward function at the end of the game is given by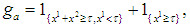 where
where 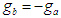 . The expected reward function is then given by
. The expected reward function is then given by 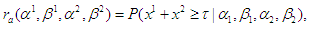 where
where 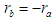 .
.4.3. Computing the Mixed Equilibria
- We compute the mixed equilibrium strategy through backtracking. Start with stage 2 given the outcome in stage 1 and assume the threshold has not been achieved, i.e.
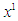 is known and less than
is known and less than 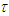 . The expected reward for player A is then given by
. The expected reward for player A is then given by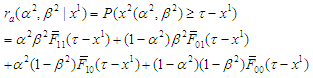 Now the problem at stage 2 becomes a single-stage zero-sum game, where the equilibrium can be obtained using the min-max decision rule (see, for example, [9]). The optimal strategies and the corresponding equilibrium at stage 2 are given by
Now the problem at stage 2 becomes a single-stage zero-sum game, where the equilibrium can be obtained using the min-max decision rule (see, for example, [9]). The optimal strategies and the corresponding equilibrium at stage 2 are given by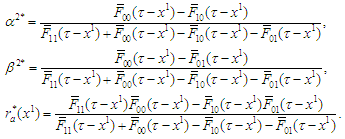 Now consider the first stage assuming the players follow the optimal strategies given above at the second stage.
Now consider the first stage assuming the players follow the optimal strategies given above at the second stage. 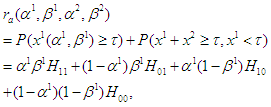 where
where 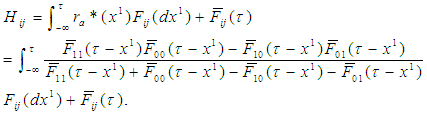 Now the game again becomes a single-stage zero-sum game, where the equilibrium can be obtained as follows
Now the game again becomes a single-stage zero-sum game, where the equilibrium can be obtained as follows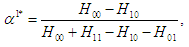 | (1) |
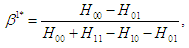 | (2) |
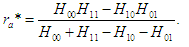 | (3) |
4.4. Numerical Calculation and Simulation
- Assume the outcomes for players A and B are the same at each stage and follow normal distributions (with different means and standard deviation 1). The distributions of the outcomes for each combination of actions are listed in table 1. Assume mixed strategies are allowed. The goal of player
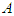 in this game is to reach a threshold
in this game is to reach a threshold 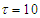 and the opponent
and the opponent 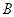 wants the opposite. The game stops whenever the threshold
wants the opposite. The game stops whenever the threshold 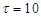 is achieved. The expected reward for player A is then given by
is achieved. The expected reward for player A is then given by 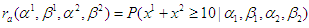 .
.
|
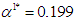 and
and 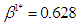 (equation (1) and (2)). The integrations in the calculation of
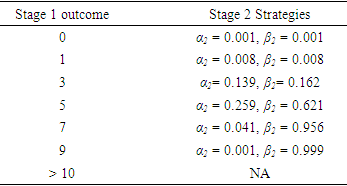
(equation (1) and (2)). The integrations in the calculation of 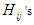 are numerical approximations since the integrals can not be obtained in closed form. The strategies of both players A and B in stage 2 will vary depending on the outcome from stage 1. Table 2 listed some examples of strategies played in the second stage. In the last example, since the goal has been achieved in stage 1, the game stopped without going into the second stage.
are numerical approximations since the integrals can not be obtained in closed form. The strategies of both players A and B in stage 2 will vary depending on the outcome from stage 1. Table 2 listed some examples of strategies played in the second stage. In the last example, since the goal has been achieved in stage 1, the game stopped without going into the second stage.
|
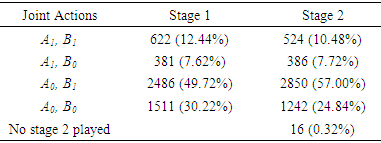
 ) for 3438 games which are 68.94% out of 5000 games. The number of times and the proportion of each joint action played at each stage are listed in Table 3.
) for 3438 games which are 68.94% out of 5000 games. The number of times and the proportion of each joint action played at each stage are listed in Table 3.
|
5. Discussion and Remarks
- In this paper, we focus on conditional decision-making in a multi-stage game with players choosing their actions simultaneously in the absence of coalitions. We defined and showed the existence of the multi-stage equilibrium. We also provide algorithm steps toward the calculation of such equilibrium using dynamic programming. Opposed to the traditional non-cooperative game setting, the joint actions of a cooperative multi-stage game can also be studied. In fact, John von Neumann and Morgenstern [10] presented a theory that analyzes various of types of coalitions that can be formed. A prefigured discussion of backward induction in a 2-person zero-sum setting is provided in their book. The multi-stage game setting discussed in this paper assumes a simultaneous game at each stage, i.e. player chooses their action without knowledge of the actions chosen by other players. Sequential behavior within a stage can also be added to the game setting, which allows the possibility that players to move in turns in each sub-game. The sequential game at each stage can be analyzed mathematically using combinatorial game theory. Equilibrium can be found using backward induction if perfect information is assumed [11]. Sequential playing simply adds an additional layer to the current dynamics.Perfect information about outcomes at previous stages is assumed in the setting of a multi-stage game. However, it is possible to imagine a game where some stages are played before the outcomes of previous stages are observed. If no information from previous stages is observed at all, the game at each stage can be treated as no different from a single-stage simultaneous game. If some, but not all the information is revealed, the analysis can become complicated depending on the structure of the information. If not all players are conscious of the other players' actions and payoffs at each stage, the backward induction analysis will not be easily applied [12].
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML