-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2021; 10(1): 1-9
doi:10.5923/j.jgt.20211001.01
Received: Mar. 18, 2021; Accepted: Apr. 26, 2021; Published: Apr. 30, 2021

About Competition Between Firms: Equilibrium or Disruption?
Olivier Lefebvre
Olivier Lefebvre Consultant, Paris, France
Correspondence to: Olivier Lefebvre, Olivier Lefebvre Consultant, Paris, France.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

One resumes the notion of “monopolistic competition” or product differentiation. The model used is Bertrand competition, the demands being deduced from the consumers’ utilities. A consumer is represented by a point ui in the cube 0 ≤ ui ≤ 1, ui being the utility of the product i for him. The product differentiation is when the points representing the consumers are in the facets of the cube ui = 1. One studies the mathematical properties of the equilibrium. Some of them correspond to the characteristics of product differentiation, which are: (1) all the consumers make a purchase. When the products are differentiated, the firms are innovative (since the preferred product of a consumer has a utility which is maximal). And innovation has been defined “struggle against no consumption” (Christensen) (2) each firm has its “garden”, consumers in the facet ui = 1 for the firm Ei. A firm keeps the consumers in its “garden”, provided its price is not too high (3) given the existence of “gardens” the profits are sufficient. Product differentiation is symmetrical, and disruption is dissymmetrical: the disruptive firm has a “garden” with a utility higher than the utilities of the “gardens” of its competitors. One demonstrates that the profit of a disruptive firm increases. The goals of the paper are: - To set out a model which describes product differentiation and disruption; - To explore the possibilities of the model used (Bertrand competition, the demands being deduced from the consumers’ utilities). The author has already used this model to study a particular kind of merger: when the merger is profitable, the bought asset being closed down. It is a sign of saturated market. Even, it could be a criterium (for saturated markets) interesting for fintechs. Also, the model allows discriminating non differentiating innovation (when there is product differentiation and all the utilities increase) and differentiating innovation (disruption: only the utility of the product of the disruptive firm increases). One shows that differentiating innovation provides more profit, always, but non differentiating innovation could provide no more profit. Finally, the model is also useful to study the effects of cannibalization. In the paper, a tractable example is set out, allowing to answer this question: is it in the interest of a disruptive firm to buy and close down a competitor before disruption? If the competitor cannibalizes the product of the disruptive firm very much, it is better to buy and close down this competitor.
Keywords: Innovation, Disruption, Bertrand competition, Cannibalization
Cite this paper: Olivier Lefebvre, About Competition Between Firms: Equilibrium or Disruption?, Journal of Game Theory, Vol. 10 No. 1, 2021, pp. 1-9. doi: 10.5923/j.jgt.20211001.01.
Article Outline
1. Introduction
- One starts from the notion of “monopolistic competition”. It was very popular among economists in the 30’s. It is a trade-off between the interests of the firms and consumers. Thanks to differentiated products the firms can choose high enough prices and their profits are sufficient. Concerning the consumers, they benefit from diverse products. More accurately, “monopolistic competition” is between “perfect differentiation of the products” and “price war”.- “Perfect differentiation of the products” means separate markets. Each firm chooses the monopoly price. There is no effect on the customers of a firm, of the prices chosen by the other firms. It is favorable to firms, which can choose enough high prices.- “Price war” means that the products are not enough differentiated, and this makes each firm decrease its price to get customers. Finally, the prices are low and the firms make no profit. It has been described as the Bertrand paradox [1]. Of course, it is favorable to consumers. “Monopolistic competition” means that the products are partially substitutable and enough differentiated. The important idea is: each firm has its “garden” (or captive customers), customers that the firm is sure to keep (even if there is a condition on the price, which should not be too high). At the equilibrium, each firm has chosen a not too high price, and benefits from its “garden”. Therefore, the profits are sufficient. Unfortunately, the two models of “monopolistic competition”, the Chamberlain’s one and the Hotelling’s one, were … erroneous [2]. It has been demonstrated later. When one applies the definition of Nash equilibrium very accurately, one demonstrates that the models were erroneous. Tirole, a French economist who was awarded the Nobel prize of economics, demonstrated that there was an error in the Chamberlain’ model [2]. And researchers demonstrated that the Hotelling’s model was erroneous [3]. In this article one proposes a new definition of “monopolistic competition”. The method is Bertrand competition, the demands being deduced from the consumers ‘utilities [4]. The “garden” of a firm Ei is the consumers with a utility ui = 1, if 1 is the maximal price. Each firm keeps the consumers in its garden, provided that its price is the lowest (for instance, if the prices are equal, each firm has for customers exactly the consumers in its garden). To simplify, one considers only three competitors and one supposes that the costs are equal to 0. The plan of the paper is:- First, one sets out the method which is used.- Then one studies the mathematical properties of the “monopolistic competition”. One demonstrates the existence of a Nash equilibrium, thanks to the Sperner’s lemma. One shows that the characteristics of product differentiation are described by the model.- One has to define “disruption”. The disruption is when one of the firms increases the utility of the consumers in its “garden”. For instance, E1 is disruptive if the utility for the consumers in its garden increases from 1 to 1, 5, while u2 = 1 and u3 = 1. In the general case, when a firm Ei increases the utilities of the consumers ui from ui to ui + k (k > 0) its profit Pi increases. One demonstrates it. However, in the particular case of “monopolistic competition” there is a difficulty. One has to set out another demonstration.- One presents two tractable examples.- A goal of the paper being to explore the possibilities of the model used, one quotes some results already achieved. They concern the profitability of mergers of some kind, when the bought asset is closed down after the merger. The model can be used also to show that there are two kinds of innovation: non differentiating innovation and differentiating innovation. And it can be used to study the role of cannibalization.- A tractable example is presented, showing the role of cannibalization. The question which is posed is the best choice for a firm which wants to disrupt: before disruption, it can buy and manage a competitor, or buy and close down it, or make no purchase. - In the Conclusion one tries to explain why disruption is an attractive choice for entrepreneurs. Also, one considers the possible following of these works.
2. The Method
- One uses the model of Bertrand competition the demands being deduced from the utilities of the consumers. This method has already been used by the author in several articles [4].The utilities for the consumers of the three products sold (u1, u2, u3) are in a cube 0 ≤ ui ≤ 1. For prices (p1, p2, p3) (0 ≤ pi ≤1) the demand Di corresponds to a “pocket” where are the consumers preferring the product of Ei and buying it. For instance, for E1 the conditions are:
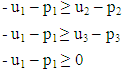 | (1) |
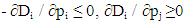 | (2) |
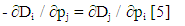 | (3) |
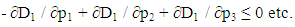 | (4) |
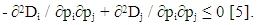 | (5) |
3. Definition of the “Monopolistic Competition”
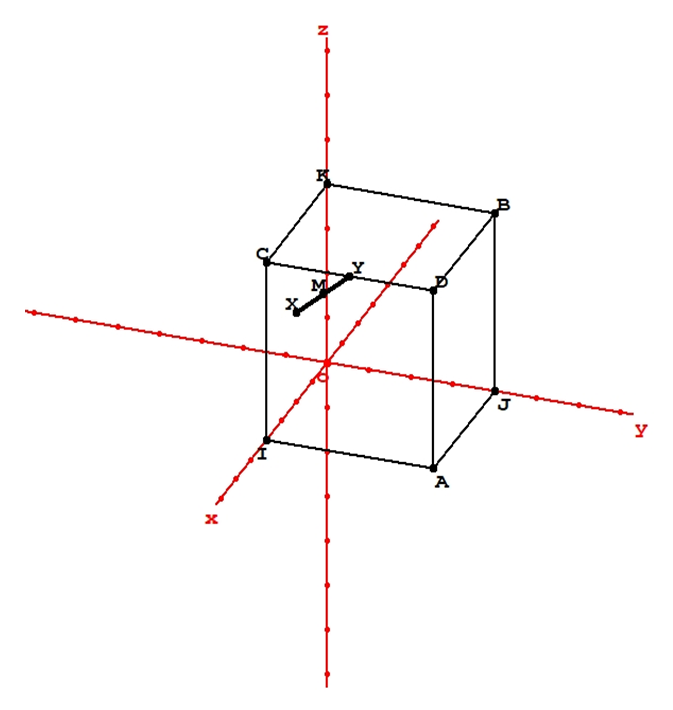
- Each firm Ei has its garden, the consumers in the facet ui = 1. All the consumers are in a garden.One sets out the particular mathematical properties of the “monopolistic competition”. The property P2 is very interesting from an economic point of view: it states that an equal increase of the prices does not change the demands. It shows why the “monopolistic competition” is advantageous for the firms: if they increase prices all together, no firm loses customers. For instance, in the symmetrical case, the prices can be 1, the maximal price, each firm keeps its “garden” (demand 1/3) and each profit is 1/3. Also, one demonstrates that there is a Nash equilibrium, thanks to the Sperner’s lemma. It is not necessary, since the Poincaré Miranda theorem could be used (the “monopolistic competition” is a particular case of Bertrand competition). But it is interesting in itself, and allows to handle the mathematical properties of the “monopolistic competition”. These mathematical properties are useful to make some demonstrations, later in the paper.These mathematical properties are:P1. For any (p1, p2, p3), all the consumers buy some product. This is obvious. Any consumer belongs to the garden of a firm Ei. Therefore ui - pi = 1 - pi ≥ O. This consumer buys the product of Ei, or another, if the net utility is more. Therefore D1 + D2 + D3 is constant. If the sum which is constant is 1: D1 + D2 + D3 = 1. P2. When (p1, p2, p3) is changed in (p1 + k, p2 + k, p3+ k) the demands remain the same. Take the example of D1 and consider (1). The two first inequalities remain valid. Now, if a consumer buying the product of E1 belongs to the garden of E1, u1 – p1 = 1 – p1 ≥ 0 remains valid. This consumer remains in the garden of E1. If the consumer buying the product of E1 belongs to the garden of E2 u2 = 1 and the first inequality u1 – p1 ≥ u2 – p2 = 1 – p2 ≥ 0 shows that u1 – p1 ≥ 0. It is the same if the consumer belongs to the garden of E3. Not only the demands but the first and second derivatives are constant when the prices increase of k. The demands are constant along a “ray” that is to say a segment parallel to the bisector (0, 0, 0), (1, 1, 1), linking an internal facet to an external facet. An example or ray is the segment (½, 0, ½), (1, ½, 1) (figure 1). One can choose a “basis” on a ray, some point M0 and all the points on the ray are represented by a parameter x: OM= OM0 + X, X being the vector (x, x, x). For instance, one can choose the middle of the ray described before, as a basis: M (¾, ¼, ¾). The parameter varies from -¼ to +¼. There is this mathematical relationship: ∂D1 / ∂p1 + ∂D1 / ∂p2 + ∂D1 / ∂p3 = 0 (and the same for j = 2 and j = 3). P3. The profit varies in a linear way along a ray. If a “basis” is chosen on the ray the price pi varies from pi0 + x1 to pi0 + x2. Therefore, the profit Pi is Pi = (pi0 + x) Di. The demand Di is constant. The profit varies in a linear way. P4 There is this mathematical relationship: ∂2D1 / ∂p12 + ∂2D1 / ∂p1∂p2 + ∂2D1 / ∂p1∂p3 = 0 (the same for j = 2 and j = 3) (6). Since D1 is constant along a ray: ∂D1 / ∂p1 + ∂D1 / ∂p2 + ∂D1 / ∂p3 = 0. The relationship (6) is obtained by deriving in p1. Also, ∂P1 / ∂p1 + ∂P1 / ∂p2 + ∂P1 / ∂p3 = D1, deriving in p1: ∂2P1 / ∂p12 + ∂2P1 / ∂p1∂p2 + ∂2P1 / ∂p1∂p3 = ∂D1 / ∂p1 < 0. Now we can demonstrate the existence of Nash equilibrium using the Sperner’s lemma.
4. Defining Disruption
- There is disruption when the gardens are not symmetrical. For instance, E1 is disruptive if u1 = 1 ,5 in its garden while u2 = 1 in the garden of E2 and u3 = 1 in the garden of E3. One defines disruption:E1 (the firm which is disruptive) increases of k (k > 0) the utilities u1 of the consumers. Therefore, the new demands are:D’1 = D1 (p1 - k, p2, p3)D’2 = D2 (p1 - k, p2, p3)D’3 = D3 (p1 - k, p2, p3).And the new profits are:P’1 = p1 D’1 P’2 = p2 D’2P’3 = p3 D’3One demonstrates that (k being small): dp2 ≤ 0, dp3 ≤ 0, dP1 ≥ 0, dP2 ≤ 0, dP3 ≤ 0. The effect (of E1 being a disruptive firm) is that the profit of E1 increases, and the profits of E2 and E3 decrease. One needs the hypothesis: the determinant of the Jacobian aij = ∂2Pi / ∂pi∂pj (i: from 1 to 3, j: from 1 to 3) is negative. The conditions (C1, C2) are sufficient but … there is a hurdle.If one considers the first tractable example presented in the paper later, one sees that the Jacobian is not defined at the equilibrium point (p1 = p2 = p3 = ½). Indeed, it could be frequent, when there is symmetry of the utilities. One calculates the demand in different cases such as p1 < p2 < p3, or p2 < p1 < p3 etc. The formulas for the demand being different is every case, possibly when p1 = p2 =p3, there is no continuity of the second derivative. And the Jacobian is not defined. In the tractable example there are different second derivatives for pi < ½ and pi > ½. But the conditions C1 and C2 are fulfilled. Considering that a price is fixed, the two other ones varying, on the bisector the reaction functions have two tangents (one below, one above the bisector, for the reaction R1). In other words, the reaction functions are made up of two different “strands” (one below, one above the bisector, for R1). One proposes a particular demonstration for this case which does not use the Jacobian (since it is not defined). One needs to demonstrate two lemmas.There are two equilibriums:- E (p10, p20, p30) is the initial equilibrium. One knows that it exists and is unique (in the case of the tractable example, because the utilities are symmetrical).- E’ (p’10, p”20, p’30) is the equilibrium after the increase of the utilities u1 (from u1 to u1 + k, k > 0). One knows that it exists (thanks to the Poincaré Miranda theorem) and one supposes it is unique. One calls S a sequence of “steps” S1 S2 S3 S1S2 S3… Si being the step when Ei maximizes its profit, the two other prices being constant. One will demonstrate that dP1 ≥ 0 (k being small) using only the conditions C1 and C2.Lemma 1: one passes from E to E’ thanks to the sequence S with: dp1 > 0 (dp1 < k), at the step 1, dp2 < 0 at the step 2, dp3 < 0 at the step 3, dp1 < 0 at the step 4 etc. One considers the deformation of the reaction functions. At each step the right strand is to consider since the rection function is made up of two “strands”. One uses inequalities such as: ∂2P1 / ∂p12 ≤ O, ∂2P1 / ∂p1∂p2 ≥ 0 etc. The decreasing sequences of the pi being bounded, there is convergence toward a limit, which is (p’10, p’20, p’30). By continuity the limit is E’, a point where a firm does not need to adjust its choice. One knows dp2 < 0 and dp3 < 0, when one passes from E to E’. One has: dP1 = -kp1 ∂D1 / ∂p1 + p1 ∂D1 / ∂p2 dp2 + p1∂D1 / ∂p3 dp3. If one demonstrates dp2 > -k (│dp2│< k) and dp3 < -k │dp3│ < k), then dP1 < 0, since dP1 > -kp1 (∂D1 / ∂p1 + ∂D1 / ∂p2 + ∂D1 / ∂p3) = 0 (Property P2).Lemma 2: When one passes from E to E’, dp2 < 0 and │dp2│ < k. The same for p3.One starts at the point P (p10, p20 – k, p30 - k) to go to E’ thanks to the sequence S. At the point P, the ∂P’I / ∂pi are positive. P’1 = p1 D1 (p1 – k, p2, p3)∂P’1 / ∂p1 = D1 (p1 – k, p2, p3) + p1 ∂D1 (p1 – k, p2, p3) / ∂p1.At the point P, ∂P’1 / ∂p1 = 0. P’2 = p2 D2 (p1 – k, p2, p3)∂P’2 / ∂p2 = D2 (p1 – k, p2, p3) + p2 ∂D2 (p1 – k, p2, p3) / ∂p2. At the point P, ∂P’2 / ∂p2 = -k ∂D2 / ∂p2 > 0.Also, ∂P’3 / ∂p3 > 0. Therefore, the sequences of pi are increasing. And they are bounded. They converge to (p’10, p’20, p’30). One knows: p20 – p’20 > 0 and p30 – p’30 > 0. Therefore, dp2 > -k and dp3 > -k.Notice that one has no proof that the equilibrium is stable (for small variations of the prices). One has not the condition of the determinant of the Jacobian which is negative, since the Jacobian is not defined. And the convergence of S when one starts from E or P does not prove the stability. The definition of the stability of the equilibrium is: for any sequence of steps (infinite, with each firm making an infinity of steps) and starting from any point, there is convergence.
5. Tractable Examples
- The first tractable example is interesting because … the demands are not linear. One supposes a density of utility which is areal, homogeneously distributed on the external facets of the cube ui = 1 (this density is equal to 1/3) (figure 2). The formulas for the demands depend of inequalities such as p1 < p2 < p3 etc.
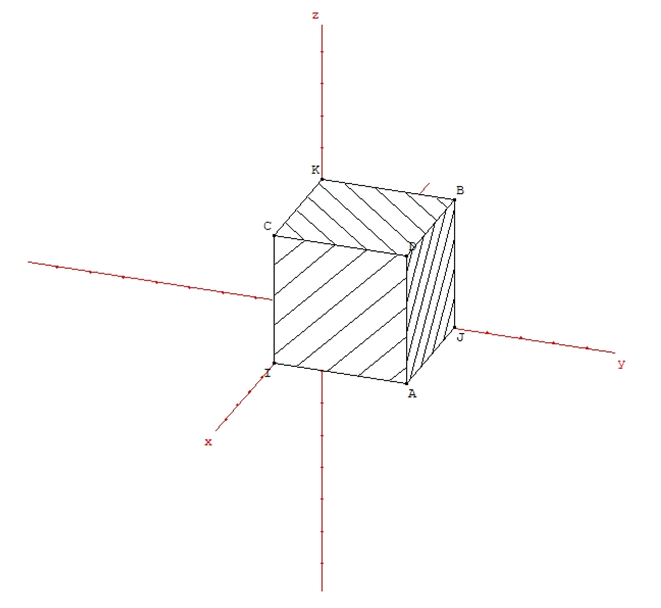 | Figure 2. In the first tractable example the density is areal, homogeneous and distributed on the external facets of the cube. These facets are stripped on the figure |
 | Figure 3. The density in the case of the second tractable example is shown. It is linear, homogeneous and distributed on the second bisectors in the external facets of the cube |
6. About the Possibilities of the Model Used
- A goal of this paper is to show the possibilities of the model used (Bertrand competition, the demands being deduced from the consumers ‘utilities). The model can be used to study the profitability of a merger, when the asset which is bought is closed, to discriminate between non differentiating innovation and differentiating innovation, and study the effects of cannibalization:Profitability of buy and close down.This kind of operation, to buy an asset and to close down it, which is supposed to be profitable (otherwise the managers would not have decided it) seems rare. Indeed, it is discrete, because the Opinion disapproves any destruction of means of production. In France, several years ago, the firm UPM (United Paper Mills) decided to close a site where paper was produced, in a village (Docelles). During a night, members of the staff destroyed the machine. It was made by night, not because it was illegal, but because it was scandalous. The destroyed machine could not be resold, and the firm lost money. But another unit of the same firm should benefit from higher prices. This compensates and besides the loss of money. It is the same calculation than in the case of “buy and close down”.The topic is interesting for several reasons:- The question of the regulator’s reaction is posed. He could disapprove this operation, which shrinks competition. But his opposition is easy to circumvent. It is easy to not invest in a branch, or to not invest enough, and some day one has to close it.- The profitability of an operation “buy and close down” is obviously a sign of saturated market. In case of Bertrand competition, a merger is always profitable (given some conditions). The profitability of a merger cannot be the sign of a saturated market. But the profitability of an operation “buy and close down” implies a strong strategic effect, because of less competition. It is explained by the saturation of a market. Two causes (when a market is saturated) are possible: (1) a competitor creates low utility for consumers, is obliged to choose a low price and “steals” customers from the other competitors (2) the products are not enough differentiated, that is to say the Bertrand paradox applies. The model used allows to present tractable models of the two kinds [4].- When the “buy and close down” is profitable, it is a reason more to choose the merger (“buy and manage”), because there is an insurance. Often to “integrate” the bought firm in the buying firm is difficult [7]. Quarrels between the two teams of managers can raise. If the “buy and close down” is profitable, it is easy to make pressure on the team of managers of the bought firm (“if you do not cooperate, we can close down the asset, it will remain profitable”). Therefore, the profitability of the “buy and close down”, if it exists, incites to merge.Non differentiating innovation and differentiating innovation.There is non differentiating innovation when an innovation is beneficial to all the competitors. In the model, all the utilities ui become ui + k (k> 0). If at the start there is product differentiation, the “gardens” correspond to the utility 1 + k. The profits increase. But there is a drawback: when the increase of all the utilities is the same, there is less product differentiation. An easy calculation which is not set out in this paper, shows this: non differentiating innovation can trigger a kind of saturated market (at the start, a “buy an close down” is not profitable, then after non differentiating innovation it becomes profitable). Let us give an “example of non-differentiating innovation. The dressmaker Karl Lagerfeld (1939 – 2019) made his career in Paris and was notorious. He worked in many firms which were in competition: in high fashion (Chanel, Fendi and his own firm), in ready to wear (Chloe, H&M) and even in sale on line (NetaPorter). Thanks to his talent, he brought innovation in several firms in competition. Therefore, the consumers ‘utilities increased. The consequence was that the profits of the firms in which he worked increased (and himself won more money). This seems to be a digression but perhaps is not. The author has stated in a paper that there is a production function of the modern artist [8]. An artist has to be visible (participating in galas, events, having a humanitarian activity, appearing in medias … to have an “image”) and to be creative (in his works). The artist’s gain is an increasing function of the two factors (visibility and creativity). In this sense, Karl Lagerfeld was really a moderncartist. He wqas an entrepreneur in visibility and creativity. His prolific activity is accurately depicted in the book “Karl Lagerfeld de A à Z” [9].At the opposite, differentiating innovation (disruption) is beneficial to a single firm, the disruptive firm. But a disruptive firm should not “buy and close down” a competitor. It is to shrink competition thanks to a means that the regulator could refuse. In his book “The innovator’s dilemma”, Christensen has explained that a firm the market of which is threatened by innovating competitors will react by protecting its market, aiming at keeping its customers thanks to an upgrade of its product. It is risky because some day the new products could replace its own [10]. Of course, there is the temptation to buy and close down the innovating firm which is a threat. The threatening firm could also be bought then its development is slowed. A famous example is Instagram bought by Facebook. It has been said that years later, Instagram could have become a real leader (as Facebook), but it has been bought by Facebook. This is made possible by the fact that it is difficult to value a start-up (in the fields of Information Technologies or bio-engineering, for instance). Examples are given in the article “Antitrust and innovation: welcoming and protecting disruption” [11]. Recently fears have appeared that the regulation in the USA, could slacken. This fear is expressed in the Philippon’s book “The great reversal: how America has given up on free markets” [12]. All this shows that the profitability of operations of “buy and close down” is an interesting topic. Since disruption is wished and welcomed, one fears an incumbent which “buys and closes down” a small, innovating firm which threats its market or its product. Effects of cannibalization.The model can be used to study the effects of cannibalization. One gives a tractable example in the following chapter.
7. A Tractable Example on Disruption
- There are often portfolios of brands in many fields: technology, fashion (clothes, leather goods, jewelry …) or medias. These brands are often in competition. These portfolios of brands in competition pose puzzling questions. Is it in the interest of the owner to choose a disruptive strategy for one of his firms, given that it will harm the other very much? Is it not in his interest to choose disruption for one of his firms and close down another? These questions could be interesting for the regulator, too. Possibly, the regulator could disagree, if the owner of several firms in competition buys a firm with the intention of not developing it, perhaps of closing down it (to develop another firm he owns). One can use the second tractable example set out in the paper to illustrate the effect of cannibalization.The disruption can be achieved in three ways: - At the start, there is equilibrium with three firms, “monopolistic competition”. One calls this game E (as equilibrium).- At the start, the disruptive firm E1 has bought E3 and will keep it. One calls this game BM (as Buy and Manage).- At the start, the disruptive firm E1 has bought E3 and will close down it. One calls this game BC (as Buy and Close down).The calculations show that E is less profitable than BC, which is less profitable than BM. How to explain that BC is less profitable than BM? In case of BC, the disruptive firm does not benefit from the profit of E3, but there is no cannibalization. At the opposite, in case of BM, the disruptive firm E1 benefits from the profit of E3, but there is cannibalization (that is to say, E3 “steals” customers from E1, and the margin is less, because p3 < p1). The calculations are needed to know what is more profitable (BM or BC).One can put it in other words. Consider BM, after disruption. One passes to BC by closing E3 (p3 = 1), then the two prices p1 and p2 change and the two profits P1 and P2 change, also. What happens when p3 becomes equal to 1? There are three kinds of customers of E3: (1) those choosing E1. It is the effect “end of cannibalization”, since these customers will allow the margin p1 instead of p3 (and p1 > p3) (2) those choosing E2 who are customers lost for E1 and (3) those choosing no purchase, who are also customers lost for E1. The demand for E1 has decreased (D1 is less after p3 → 1 than D1 + D3 before). After, there are changes of p1 and p2, and one does not know the change of D1. The calculations show that the demand D1 is less, after the close down. This explains that the profit is less. And this, notwithstanding the cannibalization which no more exists. The outcome is “reassuring” for the regulator. A disruptive firm should not buy a competitor then close down it. It should buy it and keep it. Notice that one has only examined a particular case.This question is interesting, since the disruptive firm benefits from high margins during a first period, only. There are three periods. During the first one the disruptive firm has a behavior described by speed and brand. The goal is growth. It has to make its product well known and attractive for customers. The high margins do not last a long time because during the second and third period there are entries and imitators [10]. The two last periods are necessary to make the prices of the new products lower, which is a condition of disruption according to Christensen (the products are “affordable and accessible”). During the first period, there are priorities and other goals like reduction of the costs or upgrading the distribution of the product, are neglected. And in this first period, the disruptive firm could be interested in buying a competitor, if it allows more profit.
8. Conclusions
- One has modelled “monopolistic competition”, or product differentiation, thanks to a method which is presented in the paper: Bertrand competition, the demands being deduced from the consumers’ utilities. The mathematical properties of the equilibrium, the existence of which is demonstrated, correspond to the characteristics of product differentiation: all the consumers buy a product, the competitors benefit from a “garden” (a set of customers easily kept) and the profits are sufficient. Disruption is defined: the “garden” of the disruptive firm has a utility which is more than the utilities of the “gardens” of the other competitors. One demonstrates that the profit of a firm which disrupts, increases.A goal of the paper is to explore the possibilities of the method presented. This method allows to study these topics: the profitability of mergers when the asset which is bought is closed down, the difference between non differentiating innovation and differentiating innovation (disruption) and the effects of cannibalization. Tractable examples are set out, which allow to illustrate how the method can be used. For instance, a tractable example brings an answer to the question: What it the most profitable for a disruptive firm: to “buy and manage” a competitor, to “buy and close down” it or to make no purchase? This question implies to study the effects of cannibalization.Could this method be upgraded? One can deal with this question considering three aspects:- The choice of three players. It is chosen to simplify. It would be easy to generalize the game to n players.- Neglecting the costs. Let us recall the difference between “disruptive innovation” and “efficient innovation” according to Christensen. We have already quoted the definition of “disruptive innovation”. The efficient innovation is an innovation which does not concern the product, but triggers a decrease of the costs [13]. Since the goal of this paper is to study disruptive innovation, to neglect the costs is without consequences.- The problem of moral obsolescence. It can be understood thanks to a cognitive bias, sometimes called the “dolphin bias”. It has been described, among other cognitive biases, by Nassim Taleb [14]. It concerns an inquiry on these questions: “How much money do you want to give to save dolphins?” and “How much money do you want to give to save kids from some illness?”. The results are not the same if the questions are posed separately or simultaneously. If the questions are separately posed the answers could be 50 dollars (first question) and 30 dollars (second question). If the questions are simultaneously posed, the order is reverse: 30 dollars (first question) and 50 dollars (second question). In other words, evaluation of something depends on information. When the consumers having chosen the old product are informed on the new product, their evaluation of the utility of the old product decreases (in particular when the usage implies networks). In the model used on the paper, in case of disruption one could change u1 into u1 + k (k>0), E1 being the disruptive firm, u2 into u2 – k2 (k2 > 0) and u3 into u3 – k3 (k3 > 0), E2 and E3 being the other competitors. This means that the profit P1 would increase more, and the profits P2 and P3 decrease more.The model used seems interesting, in particular, because it provides a criterium for saturated markets (the profitability of “buy and close down”). Perhaps practical applications should be possible. Market studies provide a cloud of points representing the utilities of the consumers. It corresponds approximately to an analytical function, or not. If not, a computer could be used to find the Nash equilibrium (provided that it exists and is unique). After, to calculate if the “buy and close down” is profitable, or not, should be feasible. If the “buy and close down” is profitable, it is a criterium indicating that the market is saturated.
Note
- 1. For Christensen, «disruptive innovation» allows products which are more useful and more accessible. It is the motor of economic growth. For instance, the progress in computer technology allowed mainframe computers, then personal computers, and finally smartphones.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML