-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2020; 9(1): 8-12
doi:10.5923/j.jgt.20200901.02

The President’s Dilemma: Open-up versus Lock-down Amid COVID-19 - Using Game Theory to Study the Optimal Strategies to Combat the Pandemic
Jason J. Wang
Associate Professor and Health Economist, Department of Medicine, Zucker School of Medicine at Hofstra/Northwell, Manhasset, NY, USA
Correspondence to: Jason J. Wang, Associate Professor and Health Economist, Department of Medicine, Zucker School of Medicine at Hofstra/Northwell, Manhasset, NY, USA.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Between controlling the virus and boosting the economy, it has become a “President’s Dilemma”, in which determining the optimal time to open-up the economy while still being able to contain the virus is the president’s top priority. In this study, we utilize game theory examples to illustrate various scenarios of the President’s Dilemma and provide possible game theory tools to obtain the optimal solutions. For the normal simultaneous game, the Nash equilibrium is at (Open-up, Lock-down). For the GDP vs mortality game, Open-up is a more cost-effective option. In the Bayesian game, if the proportion of the governors siding with the president q>=1/3, the President would choose Open-up while if q<1/3, he would choose Lock-down. The Stackelberg game point out the possible study path to figure out the leader-follower roles and related factors.
Keywords: COVID-19, President’s Dilemma, Bayesian game, Cost-effectiveness Analysis, Stackelberg equilibrium
Cite this paper: Jason J. Wang, The President’s Dilemma: Open-up versus Lock-down Amid COVID-19 - Using Game Theory to Study the Optimal Strategies to Combat the Pandemic, Journal of Game Theory, Vol. 9 No. 1, 2020, pp. 8-12. doi: 10.5923/j.jgt.20200901.02.
Article Outline
1. Introduction
- Since the eruption of the 2019 Novel Coronavirus (COVID-19) in Wuhan, Hubei, China in late 2019, it has quickly become a global pandemic. As of April 29, 2020, there have been over three million confirmed cases with over 218,000 deaths in 185 countries. In the United States, there have been over one million confirmed cases and over 60,000 deaths. [1] [2] [3] COVID-19 has already materially surpassed other coronaviruses such as SARS and MERS in infected cases and mortality. This pandemic has not only taken many lives but has also significantly impacted the economy. While fighting to control the virus is important, getting the economy back onto its normal course is also vital for the country. To control COVID-19, countries across the world have utilized various tactics. Aside from fast testing and tracing, these tactics also include social-distancing, stay-at-home orders, quarantining, and total lock-down. These methods have shown great efficacy in containing the virus, with China already have ended its lock-down in early April. [4] In the United States, where the president has imposed travel restrictions and all 50 states are under a major disaster declaration and are practicing social distancing and various other mechanisms, the country is currently in a state of lock-down. Although these steps have proven effective in “bending the curve” and slowing down the virus transmission, they also have slowed down the economy significantly. For example, China’s economy shrank 6.8% in the first Quarter of 2020 compared with the year-ago period, the first such contraction since Beijing began reporting quarterly gross domestic product in 1992. [5] According to Morgan Stanley, there will be a 38% drop in second-quarter U.S. GDP. [6] So, between controlling the virus and boosting the economy, it has become a “President’s Dilemma”, in which determining the optimal time to open-up the economy while still being able to contain the virus is the president’s top priority. The president has since touted the idea of opening-up the economy on May 1st [7] while the majority of state governors and public health experts still believe it is best to keep it “locked-down” for a longer period of time so that the virus will be better contained. Considering that this is an election year, the overall economic performance (GDP growth, stock market performance, and unemployment rate) is a top priority for the president but conflicts with procedures to control COVID-19 (in terms of tested cases, confirmed cases, and mortality). On the other hand, governors may prefer to first prioritize controlling the spread of the virus to limit mortality. The two parties’ priorities are seemingly in conflict. However, without the cooperation of the other party, the decisions of the president or the governors can only have partial efficacy. Presuming that the vaccines are at least one-year away [8] and that there are no effective bio-medications to treat the cases in the foreseeable future [9], this dilemma will likely not be resolved quickly.The aim of this study is to illustrate various scenarios of the President’s Dilemma and provide possible game theory tools to obtain the optimal solutions. We think this is a topic of great importance as we are creating useful guidelines for other countries that are, or will be, impacted by COVID-19 and for policymakers and researchers to prepare for future pandemics.
2. The President’s Dilemma
- In a simplified game theory setting, we have two players: the president (P) and the governors (G). Each player has two strategies: Open-up or Lock-down. Their preferences may vary from maximizing the probability of winning re-election (the president’s) to controlling the virus and minimizing the mortality (governors’). These strategies are time-sensitive (Open-up may mean to open up on May 1st, 2020 and Lock-down may instead mean to keep it locked down at that point) and are illustrative of the current situation. Figure 1 shows a portrayal of this game setting.
 | Figure 1. Strategies and Utilities |
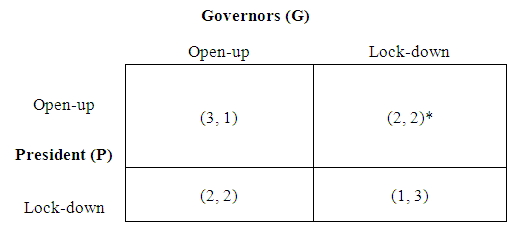 | Figure 2. Demonstrative Utility Levels |
3. Cost-Effectiveness Analysis
- We can also look at the two key elements impacted by the strategies as proxies of the utilities: GDP and Mortality. GDP encompasses stock market and unemployment, and can be used as a proxy for the overall economy. Mortality can proportionally represent the confirmed cases and thus the loss of quality adjusted life year (QALY), such that QALY equals mortality times a factor f, where f is an annualized factor related to the loss of QALY due to mortality and treatment of the infected cases, with f>>1. Figure 3 is an example to show the corresponding GDP (trillion $) and mortality (million deaths) based on some projections. [10] [11] [12]
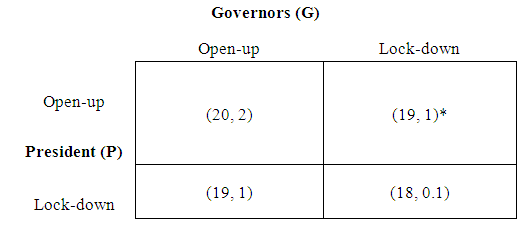 | Figure 3. GDP vs Mortality |
4. Bayesian Game Setting
- Given that certain governors may have political reasons to side with the president, the final strategy might be a mixed one. For example, in a Bayesian game setting, we have two types of governors: a certain percentage q of the governors who would prefer to be consistent with the president’s strategy, whereas 1-q of the governors will still be focusing on the virus control. With incomplete information of a governor’s type and an incentive to avoid conflicting strategies, the president’s payoff levels may be different from the numbers shown in Figure 2. First, for those governors who choose to focus on virus control (Lock-down type), the utility levels may look like the following (Figure 4a).
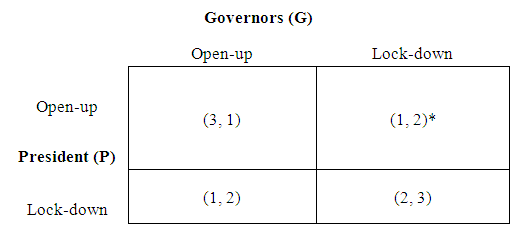 | Figure 4a. Utility Levels with the Virus-Control-First Governors |
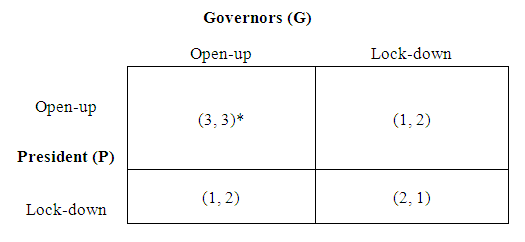 | Figure 4b. Utility Levels with the President-First Governors |
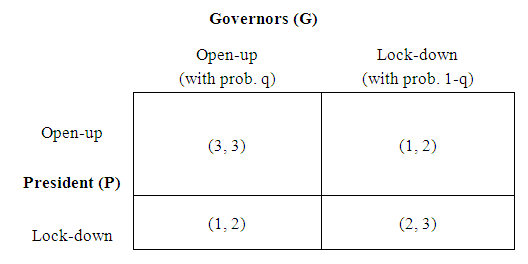 | Figure 4c. Utility Levels with Two Types of Governors |
5. The Stackelberg Model
- Based on the situation, another useful game theory tool to solve the President’s Dilemma is the Stackelberg model. We assume both the president (P) and the governors (G) choose a strategy that is rational and maximizes their utility. Decisions are influenced by the current status of COVID-19, economic factors, as well as other variables such as elections and international considerations. A decision prevails if its utility level is the highest among all the possible choices. In our current study, we assume that the players make their decisions not only with their own utility in mind, but also with consideration of the other player’s strategy as well. Following Bjorn and Vuong, [13] Hiedemann, [14] Kooreman, [15], and Wang [16], we put our study into a Stackelberg framework. A Stackelberg model is a two-player non-cooperative game model, with one player behaving as a leader while the other behaving as a follower. The leader is the person who makes the first decision (decision rule), while considering the follower's possible decisions (reaction functions). Once the leader makes his or her decision, the follower then makes his or her corresponding decision. This is a sequential process. We denote the following states:
 The above is defined as a joint decision.Following McFadden’s random utility hypothesis, [17] we define the utility functions here.P’s expected utility level corresponding to
The above is defined as a joint decision.Following McFadden’s random utility hypothesis, [17] we define the utility functions here.P’s expected utility level corresponding to 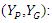
 | (1) |
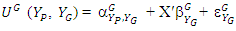 | (2) |
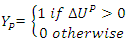 | (3) |
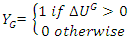 | (4) |
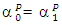 and
and 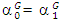 then the model collapse to a Bivariate-Probit Model, where there is no leader-follower relationship. This makes the bivariate-probit model a special case of the Stackelberg model. Assuming the President is the leader, the extensive game is displayed in Figure 5. Utilizing the backward induction method, we can obtain a sub-game perfect Stackelberg equilibrium. The same can be done with the governors as the leader.We can then derive the likelihood function as the following:
then the model collapse to a Bivariate-Probit Model, where there is no leader-follower relationship. This makes the bivariate-probit model a special case of the Stackelberg model. Assuming the President is the leader, the extensive game is displayed in Figure 5. Utilizing the backward induction method, we can obtain a sub-game perfect Stackelberg equilibrium. The same can be done with the governors as the leader.We can then derive the likelihood function as the following: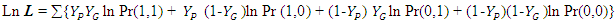 | (5) |
 With enough information about the preferences and factors for various events and time points, we can utilize this process to obtain the Stackelberg equilibrium, to test the leader-follower roles, and to evaluate the factors impacting the optimal decisions.
With enough information about the preferences and factors for various events and time points, we can utilize this process to obtain the Stackelberg equilibrium, to test the leader-follower roles, and to evaluate the factors impacting the optimal decisions. 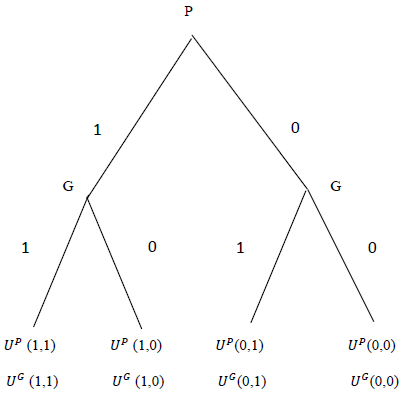 | Figure 5. The Extensive Form of the Stackelberg Game |
6. Discussion
- Game theory can provide great tools for public health and clinical studies. In the past, we have studied optimal strategies for EHR vendors and providers for system upgrades [18], identifying the leadership roles in decision making, [16] [19] and we working on projects to use game theory for medical studies. In the era of big data, game theory provides very effective and accurate methods for public health and clinical studies. For example, as we have shown earlier, the Stackelberg model includes the conventional bivariate-probit model a special case. The methods we used in this study can be applied to other research areas such as the shared decision making between doctors and patients. For example, for prostate cancer patients, there are two options: active treatment or active surveillance. What factors impact the final decision making, who is the leader in that decision between the doctors and patients, which is the optimal decision that leads to the best outcomes in various subgroups? These are all legitimate and critical questions that we are working on to get them answered. Another scenario is cancer treatment between procedures (CT/RT) and medication (Tamoxifen etc.). The third project that we are working on is to build a Bayesian game theory model to study the decision for non-symptomatic patients with small unruptured intercranial aneurysms. Current guidelines recommend radiographic follow-up of small UIAs at regular intervals with CTA or MRA to assess change in size and/or morphology. Patients might not always agree with their physician’s recommendation. Herein, we employ game theory to study the interactions between physicians and patients to determine how conflict and cooperation affect the care of small UIAs. Even for the COVID-19 cases, with enough data, we would like to know the decision making process behind certain drugs such as hydroxychloroquine, [20] and their effectiveness among different patient groups.
7. Conclusions
- In this study, we have illustrated various scenarios of the President’s Dilemma, including a normal simultaneous game, a cost effectiveness analysis in a game theory setting, a Bayesian game, and a Stackelberg game. For each of the scenarios, we have provided game theory tools to reach the optimal solutions. For the normal simultaneous game, the Nash equilibrium is at (Open-up, Lock-down). For the GDP vs mortality game, Open-up is a more cost-effective option. In the Bayesian game, if the proportion of the governors siding with the president q>=1/3, the President would choose Open-up while if q<1/3, he would choose Lock-down. The Stackelberg game point out the possible study path to figure out the leader-follower roles and related factors. With the possibility of multiple open-up and lock-down cycles, we may utilize more game theory tools (such as repeated game) to study this dilemma. This is a topic of great importance as we are creating useful guidelines for other countries that are, or will be, impacted by COVID-19 and for policymakers and researchers to prepare for future pandemics.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML