Shahd H. Alkaraz, Essam El-Seidy, Neveen S. Morcos
Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt
Correspondence to: Shahd H. Alkaraz, Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we deduce a new mathematical technique to define the winning game Tic-Tac-Toe. The results were placed in a 3x3 matrix and initial conversions were performed on the rows to find all possible win states. Programming languages were used to find the matrix to determine the diagonal wins. A simulation algorithm is presented to predict the win, or draw of a game by knowing the first move of a player. The game of Tic-Tac-Toe is simulated by using a Min-max algorithm.
Keywords:
Zaminamina Draft, Games, Combinatorics, Strategies, Decision Theory, Game Theory, Group Theory, Minimax Algorithm
Cite this paper: Shahd H. Alkaraz, Essam El-Seidy, Neveen S. Morcos, Tic-Tac-Toe: Understanding the Minimax Algorithm, Journal of Game Theory, Vol. 9 No. 1, 2020, pp. 1-7. doi: 10.5923/j.jgt.20200901.01.
1. Introduction
A game is an activity or sport usually involving skill, knowledge, or chance, which follows fixed rules and tries to win according to specific rules and principles guiding it. It includes indigenous Ghanaian games like, Pampanaa, Pi lolo, Alikoto, Kyemper, Adwoa Ata and many others [1,2]. These Combinatorial (traditional) games, in past times have been highly regarded by the elderly and young people in our society.Today, these traditional games are gradually declining and are replaced by computer aged games like Rubiks cube, Brick game, Super Mario, and the countless Facebook games. A typical example is the zaminamina board game, a traditional Ghanaian board game that is drawn using pen on a paper with different items that are used to identify both players. Example, player O (noughts) and player X (crosses). zaminamina draft is a term used in Ghana to refer to the game originated and played by the Muslims or the Fulani. The game which uses a combination of tricks that is essential part of the combinatorial game theory is similar to Shisima from Kenya, Tapatan from Philippines, Mu Torere from New Zealand among others [1,2]. It’s a simple fun game played with two players. There is a 3x3 grid formed by two vertical and two horizontal lines. And different from the games in other cultures designed as a 4x4 grid, an isosceles triangle with a line of symmetry and a mid-point line or an eight-star inscribed in a circle. It is commonly known in north America as the Tic-Tac-Toe. The zaminamina board game is played for fun, meanwhile it can be the very basis for kids to embrace mathematical knowledge and strong logical foundation when clearly defined and modelled with mathematics. It is on these grounds that this research was conducted to unveil the mathematical concepts behind the game.This type of games is considered one of the combinatorial games that should satisfy the following conditions:1. There are two players who alternate moves [1,3,4];2. There are no chance devices—hence no dice or shuffling of cards;3. There is perfect information, all possible moves are known to both players and, if needed, the whole history of the game as well;4. Play ends, regardless even if the players do not alternate moves, the game must reach a conclusion;5. The last move determines the winner, Normal play: last player to move wins. Mis `ere play: last player to move loses!
1.1. Different Names and Types for the Zaminamina Draft Game
Many board games share the element of trying to be the first to get in-a-row, and all of these games are Two-person zero-sum game involves only two players, in which the gain of one player equals the loss (payoffs) to the other player so that the total sum is zero, including Three Men’s Morris, Nine Men’s Morris, Pente, Gomoku, Qubic, Connect Four, Quarto, Gobblet, Order and Chaos, Toss Across, and Mojo.The zaminamina draft game have several variations which are modern computer games that can be traced back to ancient Egypt. Initially called Tic-Tac-Toe game, it was played by the ancient Egyptians in the Roman Empire, around the first century BC of which it was named Terni lapilli (three pebbles at a time) and instead of having any number of pieces, each player only had three, thus they had to move them around to empty spaces to keep playing [1,5]. Everything has an origin and zaminamina draft game which is currently the name given to the three in a row game had its initial names and different looks. There are different names of the game recently.Gomoku [1,6], also known as Gobang or five in a row is another abstract strategy boardgame which originated from the Japanese language gomokunarabe. It is traditionally played with Go (black and white stones) on a Go board, using 1515 of the 1919 grid intersections [1,7]. This is shown in Figure 1.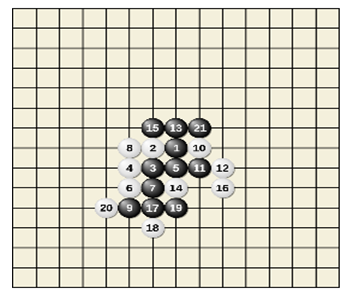 | Figure 1. Gomoku |
A modification of the gomoku game is Renju shown in Figure 2 requires 5marbles in a row or column of diagonal to signify a win for that player. | Figure 2. Renj |
Other equivalent version of the zaminamina board game is the SOS 8x8 board game in Figure 3. The objective of the game is for each player to attempt to create the straight sequence S-O-S among connected squares (either diagonally, horizontally, or vertically), and to create as many such sequences as they can [1,8].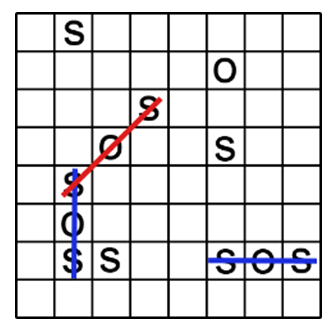 | Figure 3. SOS 8x8 board game |
A wide variation of zaminamina board game is the Ultimate Tic-Tac-Toe 3x3 grid game in which each of the nine grid squares are also divided into nine different sub squares indicating a total of 81 squares on the board. The mini squares are known as the local board and the main squares are known as the global board. This game is complex due to its nature. Before a player can even have an upper hand on a global square on the global board, that player needs to have a 3 in a row (vertical, horizontal or diagonal) before he can place either an X or an O on the global board indicating dominance [1,9]. A player wins when he gets 3 in a row (vertical, horizontal, or diagonal). This is shown in Figure 4.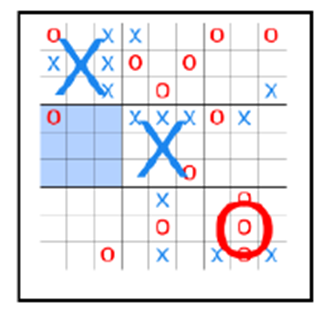 | Figure 4. Ultimate Tic-Tac-Toe |
Notakto is a Tic-Tac-Toe variant, also known as neutral or impartial Tic-Tac-Toe. According to [1,10], Notakto is a combination of tic tac toe and Nim played across one or several boards with both of the players playing the same piece (an” X” or” O”). The game ends when all the boards contain a three-in-a-row of X’s, at which point the player to have made the last move loses the game. With this type of game, the first player to complete 3 in a row loses the game and the player to complete 3 in a row last wins the game. This is shown in Figure 5. 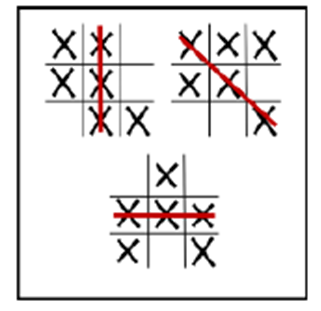 | Figure 5. Notakto |
Number Scrabble is a mathematical game where players take turns to select numbers from 1 to 9 without repeating any numbers previously used, and the first player to ac-cumulate a personal total of exactly 15 wins the game [1,11]. This is shown in Figure 6.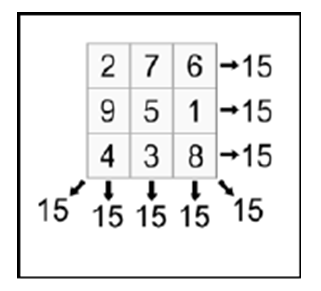 | Figure 6. Number Scrabble |
Order and Chaos is a variant of the Tic-Tac-Toe on a 66-game board invented by [1,12]. The player Order strives to create a five-in-a-row of either 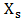 or
or 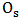 . The opponentChaos endeavors to prevent this. Unlike typical boardgames, both players control both sets of pieces (
. The opponentChaos endeavors to prevent this. Unlike typical boardgames, both players control both sets of pieces (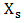 and
and 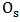 ). The game starts with the board empty. Order plays first, then turns alternate. On each turn, a player places either an X or an O on any open square. Once played, pieces cannot be moved, thus Order and Chaos can be played using pencil and paper [1,13]. Order aims to get five like pieces in a row either vertically, horizontally, or diagonally. Chaos aims to fill the board without completion of a line of five like pieces. as is shown in Figure 7.
). The game starts with the board empty. Order plays first, then turns alternate. On each turn, a player places either an X or an O on any open square. Once played, pieces cannot be moved, thus Order and Chaos can be played using pencil and paper [1,13]. Order aims to get five like pieces in a row either vertically, horizontally, or diagonally. Chaos aims to fill the board without completion of a line of five like pieces. as is shown in Figure 7. 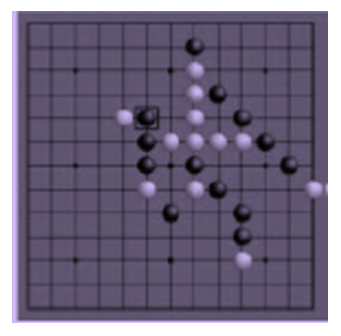 | Figure 7. Order and Chaos |
Below we will specialize in talking about the initial Tic-Tac-Toe game that consists of 3x3 grid.
2. Strategic Form of the Tic-Tac-Toe Game
There are several strategies of playing a game that will either bring you a win or a loss. The situation where a player gets a strong win is when the opponent player plays a strong lose that is to say he or she plays a mistake and the other player plays a pure strategy game to win. The strategic form of a two-person zero-sum game is given by a triplet (X, Y, A), where:a) X is a nonempty set, the set of strategies of Player I.b) Y is a nonempty set, the set of strategies of Player II.c) A is a real-valued function defined on 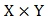 which is the 3x3 matrix grid board representation.
which is the 3x3 matrix grid board representation. 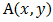 is a real number for every
is a real number for every 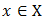 and every
and every 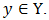 Assuming player I chooses
Assuming player I chooses 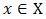 and Player II chooses
and Player II chooses 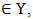 each unaware of the choice of the other. Then their choices are made known and Player I win the amount
each unaware of the choice of the other. Then their choices are made known and Player I win the amount 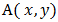 from player II. Which indicates that the mistake of player I will give player II the chance of winning the game. When
from player II. Which indicates that the mistake of player I will give player II the chance of winning the game. When 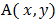 is positive, it indicates a win for Player I and if
is positive, it indicates a win for Player I and if 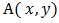 is negative, it indicates a loss of Player I over Player II. Thus,
is negative, it indicates a loss of Player I over Player II. Thus, 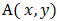 represents the winnings of player I and the losses of player II.Taking the case of
represents the winnings of player I and the losses of player II.Taking the case of 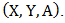 The various pure strategies of both players are that player I which is
The various pure strategies of both players are that player I which is 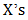 pure strategy is to have a winning game and player II which is a
pure strategy is to have a winning game and player II which is a 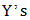 pure strategy is also to have a winning game. If both players only play with the mindset of playing an average game thereby not aiming at winning but blocking the other player from winning the game thereby bringing it to a tie. This is called mixed strategy.
pure strategy is also to have a winning game. If both players only play with the mindset of playing an average game thereby not aiming at winning but blocking the other player from winning the game thereby bringing it to a tie. This is called mixed strategy.
3. Representation of the Tic-Tac-Toe Game
The Tic-Tac-Toe game is a two-person, zero-sum game which involves either two people or a player and the computer. It is a nine square grid of which each player has only four plays to justify his winning strategies. In the absence of that, the opponent then devises a strategy to either win or bring it to a tie.The Tic-Tac-Toe game uses an alternative model known as the strategic form which represents the game as a matrix in table form. With the strategic form, we assume that both players select strategies before the game is played and uses those strategies in turn. In their first play, we define a strategy for player I and a responding strategy for player II. The payoffs matrix is shown in Table 1.Table 1. A Payoff Matrix between Player I and Player II
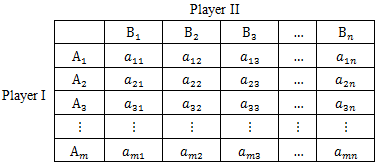 |
| |
|
Player I control rows  which are his choices and player II controls column
which are his choices and player II controls column  The game is specified by the sets of strategies available to both players and the payoff matrix. The payoff matrix tables in Table.1.
The game is specified by the sets of strategies available to both players and the payoff matrix. The payoff matrix tables in Table.1.  specifies the gain or profit to player I where
specifies the gain or profit to player I where 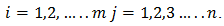 The two players select their strategies, and when player I uses strategy i and player II uses strategy j, player I receives the payoff
The two players select their strategies, and when player I uses strategy i and player II uses strategy j, player I receives the payoff 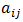 from player II. A positive number is a gain for player I and a negative number is a loss (a gain for player II). A gain to one player is a loss to the other, thus providing the zero-sum feature.
from player II. A positive number is a gain for player I and a negative number is a loss (a gain for player II). A gain to one player is a loss to the other, thus providing the zero-sum feature.
3.1. Matrix Representation of the Game Board
The Tic-Tac-Toe game has 9! =362,880 ways of filling up each square with any of the numbers from 1 to 9. Table 2. show some of the possible outcomes of the game board.Table 2. Some Possible Matrix Table of the Game Board
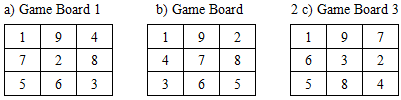 |
| |
|
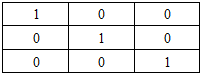
The game board in Table 2. is transformed to Row Reduced Echelon Form (RREF) in MATLAB giving out the diagonal possible wins as shown in Table 3. The possible wins were then used to design the game in Python language. The possible allocations of the plays were distorted in this way together with the corresponding results: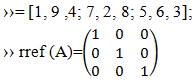
Table 3. Row Reduced Echelon Form of Matrix Table 2. (a), (b) or (c)
 |
| |
|
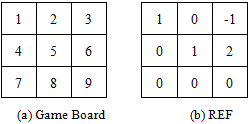
Apart from the distorted matrix, if players are to play the game in a hierarchical arrangement with player (I) playing all odd numbers and player (II) playing all even numbers, the result will not give a win. This is stems from the fact that the RREF does not produce a leading diagonal of 1 with all other entries being zero. Table 4. shows the hierarchical arrangement in matrix form and its corresponding game loss is proven by yielding a result in row echelon form (REF).Table 4. Hierarchical Arrangement of Numbers and Their RREF
 |
| |
|
3.2. Symmetry of the Game
A game is said to be symmetric if it is finite, having a square matrix and skew symmetric.The Tic-Tac-Toe game is symmetric because of its square nature and its rules in playing amongst both players. The grid is formed by two horizontal and two vertical lines, making it a 3×3 grid There are nine places that can be filled with nougats or crosses or empty position Hence, there are 39 = 19,683 possible states Each place is unique. The aim of filling the nine spaces can be considered as filling the sequence of nine boxes.Therefore, there are 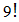 = 362,880 ways to fill the
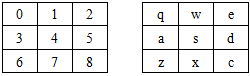
= 362,880 ways to fill the 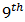 position The game can be converted to a huge tree of maximum of 19,683 nodes and 362,880 edges However, most of the states are just the reflections Therefore, these can be eliminated There are only three types of moves initially, namely – Corner, Edge and Centre. As shown in Table 5. the positions 0,2,6,8 are called ‘Corner’, 1,3,5,7 are called ‘Edge’ and position 4 is called ‘centre’ position. Further these positions are represented corresponding to qwerty keyboard inputs: q, w, e, a, s, d, z, x, c [1,14,15,16].
position The game can be converted to a huge tree of maximum of 19,683 nodes and 362,880 edges However, most of the states are just the reflections Therefore, these can be eliminated There are only three types of moves initially, namely – Corner, Edge and Centre. As shown in Table 5. the positions 0,2,6,8 are called ‘Corner’, 1,3,5,7 are called ‘Edge’ and position 4 is called ‘centre’ position. Further these positions are represented corresponding to qwerty keyboard inputs: q, w, e, a, s, d, z, x, c [1,14,15,16].Table 5. Board Position Corresponding to keyboard Input
 |
| |
|
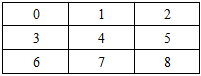
As a result, it is only necessary to consider squares 4, 3 and 0 for player I and a reduced number of squares for player II. Any moves left out are symmetric to one of those shown. Because player I goes first, the three possible plays are in square 4, 3 and 0. Given the choice of player I, player II has several remaining squares as a possible response. The symmetric nature of the game is shown in Table 6.Table 6. Symmetric Matrix Table of Tic-Tac-Toe Game Board
 |
| |
|
As experienced players observe, the result of the game is completely determined after the first player  and the second player
and the second player  have played, assuming neither player makes a mistake. Representing a win for as the value 1, a tie with a 0, and a win for as -1. Figure 8. shows the decision tree based on the first two plays. The results of the game given the first two plays are shown in the Figure 8.
have played, assuming neither player makes a mistake. Representing a win for as the value 1, a tie with a 0, and a win for as -1. Figure 8. shows the decision tree based on the first two plays. The results of the game given the first two plays are shown in the Figure 8.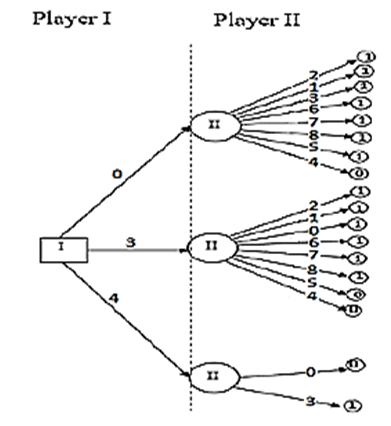 | Figure 8. Decision tree for first two plays in the Tic-Tac-Toe game |
The game is always a tie when the successive plays are made intelligently.which is a model game calling the extensive form depicts the sequential nature of the game. Even for this simple situation, the extensive form can be very large. If we had not recognized the symmetry of the game and the fact that only the first two moves are important, the tree would be very complex.
4. Winning Strategy for Tic-Tac-Toe Game
A cross ‘X’ in any of the 0,2,6,8 corner places is the best first move.The opponent player will choose from the one of the vacant places. If a ‘X’ is placed at centre at position 4, then check for corner places 0, 2, 6, and 8 and select the vacant position such that it is in accordance with the previous move This is a case of confirmed win. In case the place 4 is not empty then place the cross anywhere in 0,2,6,8 such that it is in accordance with the previous move the opponent will try to block this move and insert in between so as to avoid the player’s win. Then further move can be calculated as discussed in algorithm section.
4.1. Minimax Algorithm
Min-max is a decision-making algorithm which uses decision theory, game theory, statistics and philosophy to calculate the optimal move It is a two-player game. The mechanism evaluates minimum lose and maximum profit [17,18,19]. This logic can also be extended to play more complicated game like chess, checkers etc.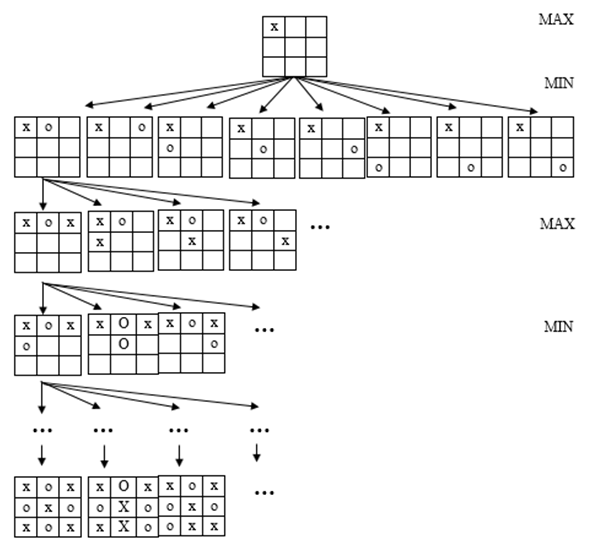 | Figure 9. Reduction of sample tree using min- max algorithm |
In the Tic-Tac-Toe game, a player tries to ensure two cases:• Maximize a player’s own chances of win.• Minimize opponent’s chances of win. Maximize profit: The profit can be maximized by either fork or win. Fork: Initially player will create opportunity where he can win in two ways.Win: If there two same X or O in a row, then play the third to get three in a row. Minimize Loss: The loss can be minimized by a block.Block: If two ‘x’ or ‘o’ of the opponent are in a row then block it, or else block opponents fork.
4.2. Logic Used by Simulator
There are two possibilities, as any one of the two players can start first [20,21,22] Firstly, consider the case when the opponent starts first, then there are following cases that can be generated:1. Opponent fills centre position 4.2. Opponent fills side position 1,3,5,7.3. Opponent fills corner position 0,2,6,8 Considering the case that  player chooses middle square Then the middle row, middle column and the two diagonals are booked Therefore, the other player is left with the option of
player chooses middle square Then the middle row, middle column and the two diagonals are booked Therefore, the other player is left with the option of  and
and 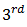 row and column Out of these four options, some will be again blocked in future moves by the opponentNow this player has following two possibilities:a. Filling the corner positionb. Filling edge positionFigure 10(a) and (b) shows the case when the opponent places a naught in the centre place and the other player places a cross at either position 0 or 8. The player books one row and one column by filling the corner positions. In figure 10(c) and (d), the player books an edge square, so in this case either one row or one column is booked. However, in both these cases there exists a case to win, so a random move can be chosen.
row and column Out of these four options, some will be again blocked in future moves by the opponentNow this player has following two possibilities:a. Filling the corner positionb. Filling edge positionFigure 10(a) and (b) shows the case when the opponent places a naught in the centre place and the other player places a cross at either position 0 or 8. The player books one row and one column by filling the corner positions. In figure 10(c) and (d), the player books an edge square, so in this case either one row or one column is booked. However, in both these cases there exists a case to win, so a random move can be chosen. | Figure 10. (a), (b), (c) and (d): Places booked by player when the opponent choses centre place |
5. Simulation the Draw and Win Payoffs
This simulation of tic tac toe needs input from QWERTY keyboard as shown in Table.5., here to book positions 0,1,2,3,4,5,6,7 and 8; keys q, w, e, a, s, d, z, x and c are used respectively.The two cases of the simulator outputs are discussed in next section. First case involves when there is a draw and in second case the player loses.
5.1. Case I
Initially player is offered the first move Hence the player can choose any position as shown in figure 11(a). To choose top left corner, key 'q' is pressed as the algorithm has nothing to evaluate, so it places ‘O’ in the centre, as shown in figure 11(b).Player again enters another corner. Now algorithm calculates the min profit of ‘X’ player and hence place ‘O’ in between as shown in figure 11(c). Then player puts a ‘X’ so that the opponent player doesn’t win in next move. The algorithm calculates max profit in the next step and places a ‘O’ at the position ‘a’. This is shown in figure 11(d). Thus, leading to a draw. This is as shown in figure 11(e). | Figure 11. a) Enter the position; b) Player choses top-left corner to place cross; c) Player again enters another corner; d) Player puts a ‘X’ to block the opponent; e) A draw |
5.2. Case II
This is the case which will result in player’s loss. In this case player plays the first move by placing X in position ‘q’. The algorithm plays the random move i.e. places a ‘O’ in the middle (as shown in figure 12(a) and 12(b)). After the player plays 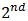 move and places a ‘X’ in middle row, first column i.e. position ‘a’, the game moves to a state where there is a less possibility of winning of the player. Hence, it calculates a step that is optimum or winning. However, there is no winning step, so computer plays the step to block the player’s winning move. So, it places a ‘O’ at position ‘Z’. To block the computer from winning, the player places a ‘X’ at top right corner. The computer computes the next optimum move at position ‘1’ and places a ‘O’ at position ‘w’. Now the player places a ‘X’ in middle row. The computer computes its next move at position ‘7’ and places a ‘O’ in bottom row middle column. The computer wins this game. These moves are shown in figure 12(a)-12(h).
move and places a ‘X’ in middle row, first column i.e. position ‘a’, the game moves to a state where there is a less possibility of winning of the player. Hence, it calculates a step that is optimum or winning. However, there is no winning step, so computer plays the step to block the player’s winning move. So, it places a ‘O’ at position ‘Z’. To block the computer from winning, the player places a ‘X’ at top right corner. The computer computes the next optimum move at position ‘1’ and places a ‘O’ at position ‘w’. Now the player places a ‘X’ in middle row. The computer computes its next move at position ‘7’ and places a ‘O’ in bottom row middle column. The computer wins this game. These moves are shown in figure 12(a)-12(h). | Figure 12. a) Players lead move; b) Computer’s move; c) Player choses position ‘a’; d) Computer’s move; e) Player choses position ‘e’; f) Computer choses position ‘1’; g) Player choses middle row; h) Computer wins |
6. Conclusions
This paper aims at deducing an intelligent mathematical technique for playing a winning game in Tic-Tac-Toe game. Also, to distort the results into a 3x3 matrix and perform an elementary row operation on the results to establish all possible wins. During the study, the3x3 square matrix was distorted and MATLAB was used to distort the matrix to establish all the possible wins.The paper presents an algorithm to predict the win cases or draw cases of the Tic-Tac-Toe game the algorithm is implemented in Java using min max algorithm. The concept of graph theory or combinational game theory is utilized to implement this game. This algorithm calculates only one step ahead using min-max algorithm In an ideal scenario, a player must calculate all the possibilities to ensure the success Tic-Tac-Toe is a small game hence an unbeatable algorithm can be developed because the state space tree generated will be small For future research study, this game algorithm can be extended to simulate other complicated games like chess and checkers However, in case of chess there are 64 squares with two players. This leads to several possibilities.
References
| [1] | K. Elvis Donkoh, Rebecca Davis, Emmanuel D.J Owusu-Ansah, A. Emmanuel Antwi, Michael Mensah, Application of combinatorial techniques to the Ghanaian Board Game Zaminamina Draft, European Journal of Pure and Applied Mathematics, Vol. 12, No. 1, 2019. |
| [2] | The Decline of Traditional Games, Retrieved from http://gijonlinenews.com/?p=3086. 2016. |
| [3] | R.J. Nowakowski, Welter’s Game, Sylver Coinage. Dots-and-Boxes, in: R.K. Guy (Ed.). Combinatorial Games, Proc. Symp. Appl. Math., Vol. 43, American Mathematical Society, Providence, RI, pp. 155182. 1996. |
| [4] | S. F. Aviezri Combinatorial Games: Selected bibliography with a succinct gourmet introduction, Available on library.msri.org/books/Book56/les/62fraenkel.pdf 2009. |
| [5] | C. Zaslavsky, Tic-Tac-Toe and other three in (I row games from ancient Egypt to the modern computer, New York: Thomas Y. Crowell. 1982. |
| [6] | Japan 101.Gomoku - Japanese Board Game 2014. |
| [7] | L. V. Allis. Searching for Solutions in Games and Artificial Intelligence (PDF), Ph.D. thesis, University of Limburg, The Netherlands. p. 123, ISBN 90-900748-8-0 1994. |
| [8] | S. Ferguson, Thomas Part I: Impartial Combinatorial Games (PDF), Game Theory (2nd ed.), Mathematics Department, UCLA, p. I-8. 2014. |
| [9] | Orlin, Ben. Ultimate Tic-Tac-Toe. Math with Bad Drawings. 2013. |
| [10] | Cram, Scott. Secrets of Nim (Notakto). 2016. |
| [11] | A. Michon, John The Game of JAM: An Isomorph of Tic-Tac-Toe. The American Journal of Psychology. Vol. 80, Issue 1, 137140. doi:10.2307/1420555, 1967. |
| [12] | Stephen Ostermiller. Tic-Tac-Toe Strategy, Retrievedfrom https://blog.ostermiller.org/Tic-Tac-Toe-strategy. |
| [13] | Cassan, Ferdinand de. Austrian Games Museum, Retrieved from www.ludorium.at. |
| [14] | B. Brendan O’Donoghue, "Min-Max Approximate Dynamic Programming", IEEE Multi-Conference on Systems and Control, pp. 28-30, 2011. |
| [15] | R.L, Rivest, "Game Tree Searching by Min / Max Approximation", Artificial Intelligence 12(1), pp. 77-96, 1988. |
| [16] | J Chen,.; Wu, I.; W Tseng,.; B Lin,.; and C Chang,. “Job-level alpha-beta search”, IEEE Transactions on Computational Intelligence and AI in Games, 2014. |
| [17] | S. Gelly,; , L. Kocsis; M Schoenauer; M Sebag,.; D Silver,.; Szepesvári,; C. O.Teytaud,; “The grand challenge of computer Go: Monte Carlo tree search and extensions”, Communications of the ACM, 55(3), 2012. |
| [18] | Y. Cai and C. Daskalakis, "On minmaxtheorems for multiplayer games", 22nd Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '11), pp. 217-234, 2011. |
| [19] | C. Daskalakis, C. H. Papadimitriou, Continuous Local Search. In: SODA 2011. |
| [20] | B. Huang, "Pruning Game Tree by Rollouts", 29th AAAI Conference on Artificial Intelligence, pp. 1165-1173, 2015. |
| [21] | S. Gal, “A discrete search game”, SIAM Journal of Applied Mathematics 27(4), pp. 641-648, 1974. |
| [22] | H. W. Kuhn, Classics in Game Theory, Princeton University Press, 1997. |








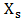 or
or 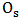 . The opponentChaos endeavors to prevent this. Unlike typical boardgames, both players control both sets of pieces (
. The opponentChaos endeavors to prevent this. Unlike typical boardgames, both players control both sets of pieces (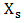 and
and 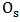 ). The game starts with the board empty. Order plays first, then turns alternate. On each turn, a player places either an X or an O on any open square. Once played, pieces cannot be moved, thus Order and Chaos can be played using pencil and paper [1,13]. Order aims to get five like pieces in a row either vertically, horizontally, or diagonally. Chaos aims to fill the board without completion of a line of five like pieces. as is shown in Figure 7.
). The game starts with the board empty. Order plays first, then turns alternate. On each turn, a player places either an X or an O on any open square. Once played, pieces cannot be moved, thus Order and Chaos can be played using pencil and paper [1,13]. Order aims to get five like pieces in a row either vertically, horizontally, or diagonally. Chaos aims to fill the board without completion of a line of five like pieces. as is shown in Figure 7. 
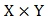 which is the 3x3 matrix grid board representation.
which is the 3x3 matrix grid board representation. 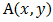 is a real number for every
is a real number for every 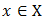 and every
and every 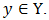 Assuming player I chooses
Assuming player I chooses 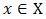 and Player II chooses
and Player II chooses 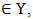 each unaware of the choice of the other. Then their choices are made known and Player I win the amount
each unaware of the choice of the other. Then their choices are made known and Player I win the amount 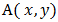 from player II. Which indicates that the mistake of player I will give player II the chance of winning the game. When
from player II. Which indicates that the mistake of player I will give player II the chance of winning the game. When 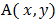 is positive, it indicates a win for Player I and if
is positive, it indicates a win for Player I and if 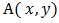 is negative, it indicates a loss of Player I over Player II. Thus,
is negative, it indicates a loss of Player I over Player II. Thus, 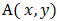 represents the winnings of player I and the losses of player II.Taking the case of
represents the winnings of player I and the losses of player II.Taking the case of 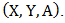 The various pure strategies of both players are that player I which is
The various pure strategies of both players are that player I which is 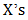 pure strategy is to have a winning game and player II which is a
pure strategy is to have a winning game and player II which is a 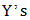 pure strategy is also to have a winning game. If both players only play with the mindset of playing an average game thereby not aiming at winning but blocking the other player from winning the game thereby bringing it to a tie. This is called mixed strategy.
pure strategy is also to have a winning game. If both players only play with the mindset of playing an average game thereby not aiming at winning but blocking the other player from winning the game thereby bringing it to a tie. This is called mixed strategy. 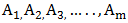 which are his choices and player II controls column
which are his choices and player II controls column 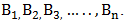 The game is specified by the sets of strategies available to both players and the payoff matrix. The payoff matrix tables in Table.1.
The game is specified by the sets of strategies available to both players and the payoff matrix. The payoff matrix tables in Table.1. 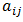 specifies the gain or profit to player I where
specifies the gain or profit to player I where 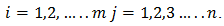 The two players select their strategies, and when player I uses strategy i and player II uses strategy j, player I receives the payoff
The two players select their strategies, and when player I uses strategy i and player II uses strategy j, player I receives the payoff 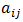 from player II. A positive number is a gain for player I and a negative number is a loss (a gain for player II). A gain to one player is a loss to the other, thus providing the zero-sum feature.
from player II. A positive number is a gain for player I and a negative number is a loss (a gain for player II). A gain to one player is a loss to the other, thus providing the zero-sum feature.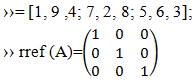
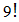 = 362,880 ways to fill the
= 362,880 ways to fill the 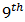 position The game can be converted to a huge tree of maximum of 19,683 nodes and 362,880 edges However, most of the states are just the reflections Therefore, these can be eliminated There are only three types of moves initially, namely – Corner, Edge and Centre. As shown in Table 5. the positions 0,2,6,8 are called ‘Corner’, 1,3,5,7 are called ‘Edge’ and position 4 is called ‘centre’ position. Further these positions are represented corresponding to qwerty keyboard inputs: q, w, e, a, s, d, z, x, c [1,14,15,16].
position The game can be converted to a huge tree of maximum of 19,683 nodes and 362,880 edges However, most of the states are just the reflections Therefore, these can be eliminated There are only three types of moves initially, namely – Corner, Edge and Centre. As shown in Table 5. the positions 0,2,6,8 are called ‘Corner’, 1,3,5,7 are called ‘Edge’ and position 4 is called ‘centre’ position. Further these positions are represented corresponding to qwerty keyboard inputs: q, w, e, a, s, d, z, x, c [1,14,15,16].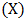 and the second player
and the second player 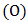 have played, assuming neither player makes a mistake. Representing a win for as the value 1, a tie with a 0, and a win for as -1. Figure 8. shows the decision tree based on the first two plays. The results of the game given the first two plays are shown in the Figure 8.
have played, assuming neither player makes a mistake. Representing a win for as the value 1, a tie with a 0, and a win for as -1. Figure 8. shows the decision tree based on the first two plays. The results of the game given the first two plays are shown in the Figure 8.

 player chooses middle square Then the middle row, middle column and the two diagonals are booked Therefore, the other player is left with the option of
player chooses middle square Then the middle row, middle column and the two diagonals are booked Therefore, the other player is left with the option of  and
and  row and column Out of these four options, some will be again blocked in future moves by the opponentNow this player has following two possibilities:a. Filling the corner positionb. Filling edge positionFigure 10(a) and (b) shows the case when the opponent places a naught in the centre place and the other player places a cross at either position 0 or 8. The player books one row and one column by filling the corner positions. In figure 10(c) and (d), the player books an edge square, so in this case either one row or one column is booked. However, in both these cases there exists a case to win, so a random move can be chosen.
row and column Out of these four options, some will be again blocked in future moves by the opponentNow this player has following two possibilities:a. Filling the corner positionb. Filling edge positionFigure 10(a) and (b) shows the case when the opponent places a naught in the centre place and the other player places a cross at either position 0 or 8. The player books one row and one column by filling the corner positions. In figure 10(c) and (d), the player books an edge square, so in this case either one row or one column is booked. However, in both these cases there exists a case to win, so a random move can be chosen.

 move and places a ‘X’ in middle row, first column i.e. position ‘a’, the game moves to a state where there is a less possibility of winning of the player. Hence, it calculates a step that is optimum or winning. However, there is no winning step, so computer plays the step to block the player’s winning move. So, it places a ‘O’ at position ‘Z’. To block the computer from winning, the player places a ‘X’ at top right corner. The computer computes the next optimum move at position ‘1’ and places a ‘O’ at position ‘w’. Now the player places a ‘X’ in middle row. The computer computes its next move at position ‘7’ and places a ‘O’ in bottom row middle column. The computer wins this game. These moves are shown in figure 12(a)-12(h).
move and places a ‘X’ in middle row, first column i.e. position ‘a’, the game moves to a state where there is a less possibility of winning of the player. Hence, it calculates a step that is optimum or winning. However, there is no winning step, so computer plays the step to block the player’s winning move. So, it places a ‘O’ at position ‘Z’. To block the computer from winning, the player places a ‘X’ at top right corner. The computer computes the next optimum move at position ‘1’ and places a ‘O’ at position ‘w’. Now the player places a ‘X’ in middle row. The computer computes its next move at position ‘7’ and places a ‘O’ in bottom row middle column. The computer wins this game. These moves are shown in figure 12(a)-12(h). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





