-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2019; 8(2): 38-41
doi:10.5923/j.jgt.20190802.03

The Shifted Alliance System of Last Nim Game
Hassan El Kady, Essam El-Seidy
Department of Mathematics, Faculty of Science, Ain Shams University, Egypt
Correspondence to: Hassan El Kady, Department of Mathematics, Faculty of Science, Ain Shams University, Egypt.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We introduce a class of impartial combinatorial game which is the multi-player Last Nim game, denoted by 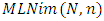 in which there are N piles of counters which are linearly ordered, the move will be, the n-player will remove any positive integer of counters from the last pile, we will introduce this
in which there are N piles of counters which are linearly ordered, the move will be, the n-player will remove any positive integer of counters from the last pile, we will introduce this 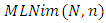 with Shifted Standard alliance system by 1, denoted by
with Shifted Standard alliance system by 1, denoted by 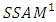 in which each player will prefer winning for another player over himself. The Aim is to determine the game value of the positions of
in which each player will prefer winning for another player over himself. The Aim is to determine the game value of the positions of 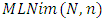 where
where 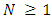 is the number of piles and
is the number of piles and 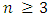 is the number of players and we will present the possible
is the number of players and we will present the possible 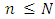 and determine the game value in this case.
and determine the game value in this case.
Keywords: Shifted, Alliance, MLNim(N,n), Nim and Impartial combinatorial game
Cite this paper: Hassan El Kady, Essam El-Seidy, The Shifted Alliance System of Last Nim Game, Journal of Game Theory, Vol. 8 No. 2, 2019, pp. 38-41. doi: 10.5923/j.jgt.20190802.03.
Article Outline
1. Introduction
- Combinatorial game theory is a part of mathematics science committed to concentrate the ideal procedure in perfect information data games where commonly two players are included. In a 2-player perfect information game two players substitute moves until one of them cannot move at this turn. Among the games of this sorts, as a non-comprehensive rundown, are Nim Bouton [1], Fraenkel and Lorberbom [2], Flammenkamp [3], Holshouser [4], Albert and Nowakowski [5], Liu and Zhao [6], End-Nim (Albert and Nowakowski [7]), and so on. Last Nim with two players presented by Friedman [8] is played with heaps of counters which are straightly requested. The two players alternate removing any position whole number of counters from the last heap. Under normal play, all P-positions of Last Nim with two players are those containing an odd number of heaps containing one counter.
1.1. Multi-Player Combinatorial Game
- Amid the most recent couple of years. The theory of 2-player perfect information games has been generally examined. Normally, it is important to sum up however much as could reasonably be expected of the theory of n-player games. In 2-player perfect information games, one can discuss what the result of the diversion ought to be, at the point when every players play it right, i.e. at the point when every player embraces an ideal strategy yet when there are multiple players', it may not well discuss similar thing. For example, it might so happen that one of the players can help any of the players to win, yet at any rate, he himself needs to lose. Along these lines, the result of the game relies upon how alliances are shaped among the players, in past studies a few conceivable outcomes were researched: multi-player without alliance, multi-player with two alliances and multi-player with alliance system.
1.1.1. Multi-Player without Alliance
- N-player Nim game has been submitted without alliance by Li [9]. Straffin [10] tried to classify the three player Nim game with somewhat restrictive assumption regarding the behavior of each player. This work investigated by Loeb [11] by introducing the concept of stable alliance (where an alliance member wins) the work done by Propp [12] analyzed the conditions required to allow one player has a winning strategy against the combined force of the other. Cincotti [13] gave an analysis of n-player partisan games.
1.1.2. Multi-Player with Two Alliances
- Kelly ([14], [15]) introduced one bonded Nim, denoted by OBN, which is considered as one pile Nim with two alliance and n-player, any player in this will help his alliance to win, under normal play, the player who removes the last counter will win but under misere play, the player who removes the last counter will lose. The general structures of two alliances were introduced by Zhao and Liu [16].
1.1.3. Multi-Player with Alliance System
- Krawec ([17], [18]) considered that every player has a fixed set of alliance, i.e. he will arrange according to preference and this alliance system will be known before beginning the game and this alliance system presented by a matrix. Also he improved a method of analyzing the impartial combinatorial game with n player and considered that one of the players play randomly with no strategy, El-Seidy, El kady and Nassar [19] studied the multi-player Last Nim with any alliance system and they made a program which solved the game for any alliance system.
1.1.4. Multiple-Player with Alliance System with Pass
- Liu and Yang [20] studied the multiple-player Last Nim when the standard alliance matrix adopted in, this matrix we will explain it below, each of n players either removes any positive integer of counters from the last pile or makes a choice 'pass'. Once a 'pass' option is used, the total number s of passes decreases by 1. When all s passes are used, no player may ever 'pass' again. A pass option can be used at any time, up to the penultimate move, but cannot be used at the end of the game, he determined the game value of the game with different number of piles and players.
2. Multiple-Player Last Nim with Alliance
- In this section, we will introduce the Multiple-player Last Nim with alliance and we will introduce the alliance system, the standard alliance system and the game value function which help us to get our results.
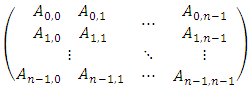 where
where 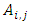 determines which player is most preferred choice for the player
determines which player is most preferred choice for the player 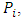 and the left-most entries being more preferred over the right-most entries.Definition 2.1. The standard allaince matrix (for brevity SAM) where
and the left-most entries being more preferred over the right-most entries.Definition 2.1. The standard allaince matrix (for brevity SAM) where 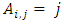
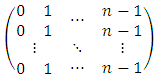 If we adopt SAM then for each
If we adopt SAM then for each 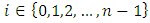 , player
, player 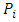 prefers
prefers 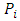 over
over 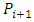 over… over
over… over 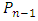 over
over 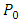 over … over
over … over 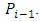 Definition 2.2. Using above definitions, Krawec [17] introduced a function
Definition 2.2. Using above definitions, Krawec [17] introduced a function 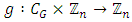 (where
(where 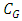 denotes the set of all impartial combinatorial games,
denotes the set of all impartial combinatorial games, 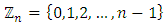 )
)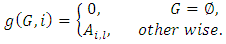 | (1) |
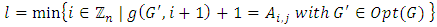 Using the above equation Liu and Yang [20] considered any position of MLNim(N; n) as
Using the above equation Liu and Yang [20] considered any position of MLNim(N; n) as 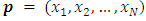 which has two options are
which has two options are 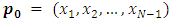 and
and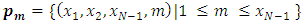 then the game value function takes the form:
then the game value function takes the form: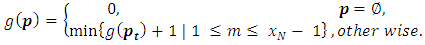 | (2) |
3. The Shifted Alliance System of Multi-Player Last Nim
- We introduce another alliance matrix is called the shifted alliance matrix by r (for brevity
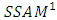 ) in this matrix
) in this matrix 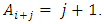 If
If 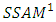 is adoptedwe have
is adoptedwe have 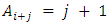 then
then 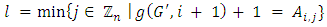
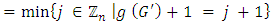
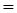
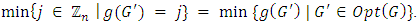
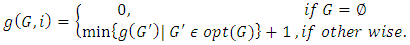 | (3) |
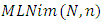 as a vector
as a vector 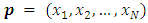 that can move in two ways. To it, which are
that can move in two ways. To it, which are 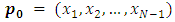 and
and 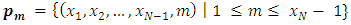 therefore, the game value function will take the following form
therefore, the game value function will take the following form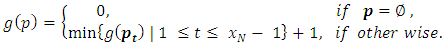 Definition 3.2. the alliance matrix will be shifted by 1 and will take the form:
Definition 3.2. the alliance matrix will be shifted by 1 and will take the form: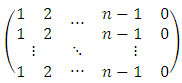 If we adopt
If we adopt 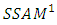 then for each
then for each 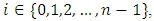 player
player 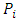 prefers
prefers 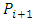 over
over 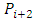 over…over
over…over 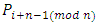 over
over 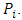 Theorem 3.3. For MLNim(N,n) and consider any position vector
Theorem 3.3. For MLNim(N,n) and consider any position vector 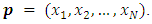 If
If 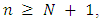 thus
thus 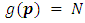 for all
for all 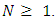 Proof. First for
Proof. First for 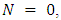 then
then 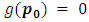 because
because 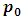 has no any position can move to it. We will continue by induction on
has no any position can move to it. We will continue by induction on 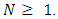 (i) If
(i) If 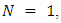 by induction on
by induction on 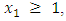 we will prove that
we will prove that 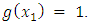 If
If 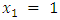 we have
we have 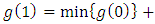
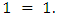 For
For 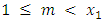 suppose that
suppose that 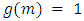 then
then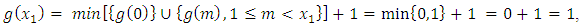 then for all
then for all 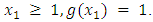 (ii) Suppose that for
(ii) Suppose that for 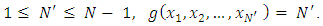 We will take any
We will take any 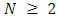 and by induction on
and by induction on 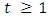 we will prove that
we will prove that 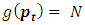 Base case:
Base case: 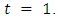 Then
Then 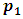 can move to only one position
can move to only one position 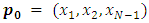 with
with 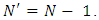 By induction assumption on
By induction assumption on 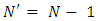 we have
we have 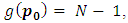 then
then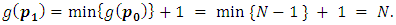 Induction step:
Induction step: 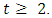 For all
For all 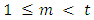 suppose that
suppose that 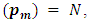 then
then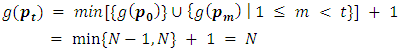 | (4) |
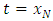 then
then 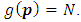 Theorem 3.4. For MLNim(n+d,n) and consider any position vector
Theorem 3.4. For MLNim(n+d,n) and consider any position vector 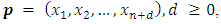
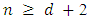 then
then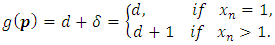 | (5) |
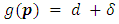 by induction on
by induction on 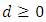 (I) If
(I) If 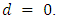 For
For 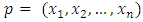 we will prove that
we will prove that 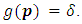 We have two cases:(i) If
We have two cases:(i) If 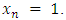 we will prove that
we will prove that 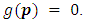 Let
Let 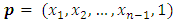 then
then 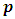 has only one position can move to it, which is
has only one position can move to it, which is 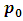 which is a vector position of
which is a vector position of 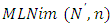 such that
such that 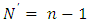 thus
thus 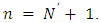 Theorem (3.3) gives that
Theorem (3.3) gives that 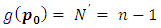 then
then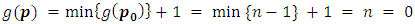 (ii) For
(ii) For 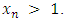 We will prove that
We will prove that 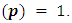 we will prove by induction on
we will prove by induction on 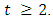 If
If 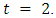 Then
Then 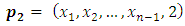 has two positions can move to it
has two positions can move to it 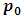 and
and 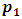 . For
. For 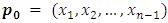 which is a position vector of
which is a position vector of 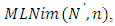 where
where 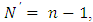 then
then 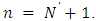 Theorem (3.3) gives
Theorem (3.3) gives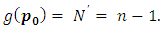 For
For 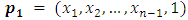 which has only one position can move to it, which is
which has only one position can move to it, which is 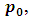 then
then 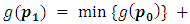
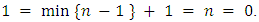 Then
Then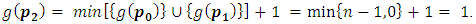 Induction step:
Induction step: 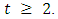 Assume that
Assume that 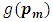 = 1 for
= 1 for 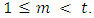 Then
Then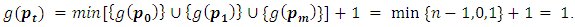 (II) Induction step:
(II) Induction step: 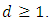 Assume that
Assume that 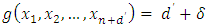 for
for 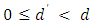 and
and 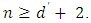 we will prove that
we will prove that 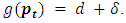 We have
We have 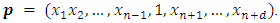 By induction on
By induction on 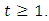 If
If 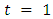 then
then 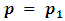 has only one position can move to it, which is
has only one position can move to it, which is 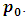 The induction assumption then
The induction assumption then 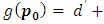
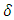 then
then 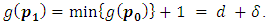 Induction step:
Induction step: 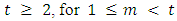 suppose that
suppose that 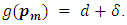 Thus
Thus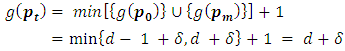 | (6) |
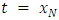 , then
, then 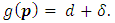 Theorem 3.5. For MLNim(N,n) and consider any position vector
Theorem 3.5. For MLNim(N,n) and consider any position vector 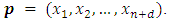 If
If 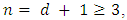 thus,
thus,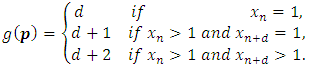 | (7) |
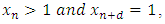 then
then 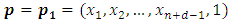 has only one option
has only one option 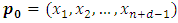 , by letting
, by letting 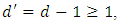 we have
we have 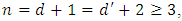 then by theorem (3.4) we have
then by theorem (3.4) we have 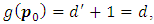 thus
thus 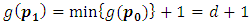 Hence
Hence 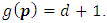 (ii) If
(ii) If 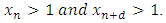 By induction on
By induction on 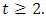 Base case:
Base case: 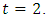 Now
Now 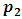 has two options
has two options 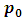 and
and 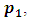 from (i) we have
from (i) we have 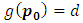 and
and 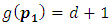 then
then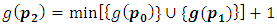
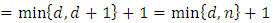
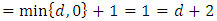 (iii) If
(iii) If 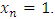 We will prove that
We will prove that 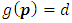 by induction on
by induction on 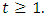 Base case:
Base case: 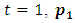 has only one option
has only one option 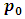 of
of 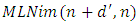 where
where 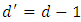 then
then 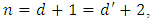 by theorem (3.4)
by theorem (3.4) 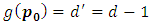 then
then 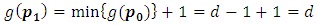 Induction step:
Induction step: 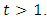 Suppose that
Suppose that 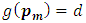 such that
such that 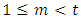 then
then 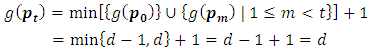 | (8) |
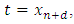 we have
we have 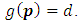
4. Conclusions
- In or article we studied the multi-player Last Nim game in the case of the shifted alliance matrix by one this mean that the each player not prefer himself to win but he prefers the next player who plays after him and we studied the game value function in different cases:• If the
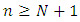 , where
, where 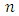 is the number of players and
is the number of players and 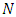 is the number of piles we proved that
is the number of piles we proved that 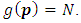 This means that the game value function equal the number of piles.• If
This means that the game value function equal the number of piles.• If 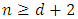 where
where 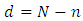 we proved that
we proved that 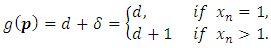
5. Future Work
- All results given by our paper is based on the assumption that the shifted standard alliance matrix by 1 is adopted and we considered our game without pass.In the future we will do the following:(i) apply the shifted alliance matrix in case of MLNim(N,n) with pass.(ii) We will study the MLNim(N,n) for the shifted alliance matrix by
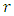 for
for 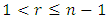 .(iii) we will apply the shifted alliance matrix on different games like Small Nim, Subtraction, games, Wythoff's game, etc.
.(iii) we will apply the shifted alliance matrix on different games like Small Nim, Subtraction, games, Wythoff's game, etc. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML