Wesam B. Zorik, Essam EL-Seidy, Entisarat M. Elshobaky
Department of Mathematics, Faculty of Science, Ain Shamus University, Cairo, Egypt
Correspondence to: Wesam B. Zorik, Department of Mathematics, Faculty of Science, Ain Shamus University, Cairo, Egypt.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Zero Determinant (ZD) strategies is a new class of probabilistic and conditional strategies discovered by Press and Dyson which has been applied on two players. ZD strategies for multiple players will be explored where the application of ZD has been taken on Iterated three-player Prisoner’s Dilemma Game (IPDG) with two actions C or D. It is assumed that the results in the case of the three players correspond to what was obtained in the case of two players with different calculation methods. It is interesting, although the player who adopts ZD strategies can determine the opponent’s payoffs in a unilateral way. And with an extortion strategy, he can impose a linear relationship between the expected return for him and the expected payoff of other players, but he cannot determine his own score. Also, the yield matrix was determined in the case of three players.
Keywords:
Iterated Prisoner’s Dilemma Game IPDG, Payoff Matrix, Multi-player Game, Zero, Determinate Strategy, Extortionate strategies
Cite this paper: Wesam B. Zorik, Essam EL-Seidy, Entisarat M. Elshobaky, Zero-Determinate Strategies for Iterated Three-Player Game, Journal of Game Theory, Vol. 8 No. 2, 2019, pp. 32-37. doi: 10.5923/j.jgt.20190802.02.
1. Introduction
The mathematical theory of games was invented by John von Neumann and Oskar Morgenstern. When they published their book "Theory of Games and Economic Behavior" 1944 [1]. As an extension of this theory, Nash classified a game as either non-cooperative game or cooperative game. And set the notation of an equilibrium point (Nash equilibrium) of a non-cooperative game in 1949 [2]. Game theory generally refers to the study of mathematical models that describe the behavior of logical decision-makers. It is widely used in many fields such as economics [3,4], political science [5], Network [6], biology [7], Computer Science [8], etc., and can be used to model many real-world scenarios. Games are classified into: Zero-sum game, symmetric game, coordination game, sequential, simultaneous game, etc. [9]. And we are interested in the symmetric games such as prisoner’s dilemma.
1.1. Prisoner’s Dilemma Game
Prisoner’s Dilemma PD was originally framed by Merrill Flood and Melvin Dresher while working at Rand corporation in 1950. Albert W. Tucker formalized the game with prison sentence rewards and named it "Prisoner's Dilemma". PD Game is the best-known strategy game in social science. And a very useful tool for strategic decision-making [10]. The PD Game is called the Iterated Prisoner’s Dilemma Game (IPDG) when the same players repeat the game many times, each player has the chance to deduce the style of play for the other party. And a repeated game allows a player to analyze the game and eliminate the strategies that will never be used [11]. In iterated 2x2 Prisoner’s Dilemma Game IPDG, two players face each other and each has two choices either cooperate (D) or defect (C). Each player gets scores based on his choice compared to choosing his opponents. And makes his decision without knowing the next step of other players. If the two players choose cooperate (C) they are rewarded with R. If one defects (D), the defectors gets an even larger payoff T, while the cooperator gets a small payoff S. If both choose defect (D), then both get a payment P. The classical payoff matrix for the PD game must satisfy inequalities: T > R > P > S where the Nash equilibrium of the game is mutual defection, whereas 2R > T+S makes mutual cooperation the globally best outcomes [12]. The payoff matrix for one round of PD game represented by [12, 13]: 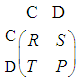 | (1) |
Where the payoff vector can be determined for the players X, Y by SX =(R, S, T, P), SY =(R, S, T, P). Actually, it is not clear which strategy is the best when the PD game is repeated infinitely and meets the same players many times. As a result, in 2012 Press and Dyson dramatically changed people’s understanding of this problem by deriving what they called Zero Determinant ZD strategies [13]. There is particular interest in a subset of ZD strategies, called extortion strategies [13,17,18], through which an extortion linear relationship can be imposed between the players’ scores by the player who use ZD strategies. In iterated play of a fixed game, it is possible to believe that a player say Y with longer memory of past outcomes has advantage over a more forgetful player say X. But in fact, it can be proved that for any strategy of the longer-memory player Y, X’s score is exactly the same as if Y has had played a certain short-memory strategy [13-15].
1.2. Three-Player IPDG
ZD strategies in IPDG can be extended naturally to include more than two players in the game so focus on the iterated three- player game. Where in the one round there are eight possible outcomes (states) xyz = {CCC, CCD, CDC, CDD, DCC, DCD, DDC, DDD} [16,19,20]. Where x, y and z represent X’s, Y’s and Z’s choices respectively, C for cooperate and D for defect. For X, both states are considered CCD and CDC are the same because the important is the cooperation of one of the players and defection the otherwhile it is not important for him which one of the other players cooperate or defect, this is point of view of other players as well. Therefore, a strategy vector for each player consist of 8-dimentional vector with 6 independent variables. A memory-one strategy represented by eight tuples specifying the probability of cooperation in the current round given the outcome of the previous move whether it was cooperation or defection. Therefore, according to the previous eight outcomes X’s strategy can be represented by the vector 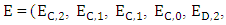
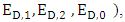 Y’s strategy by the vector
Y’s strategy by the vector 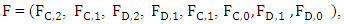 and Z’s strategy by the vector
and Z’s strategy by the vector 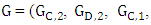
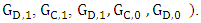 The possibility of cooperation can be denoted by
The possibility of cooperation can be denoted by 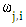 : j denotes player
: j denotes player 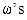 previous move and i represents the number of cooperating of
previous move and i represents the number of cooperating of 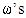 opponents in the previous round,
opponents in the previous round, 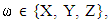
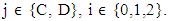 For example, if
For example, if 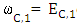 denote the probability that X player play cooperate after the outcome CDC or CCD in the previous round, and
denote the probability that X player play cooperate after the outcome CDC or CCD in the previous round, and 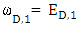 denote the probability that X player play cooperate after the outcome DCD or DDC in the previous round, this point of view applies for each player.
denote the probability that X player play cooperate after the outcome DCD or DDC in the previous round, this point of view applies for each player.
1.2.1. Three-Player IPDG
According to the previous section, we have the payoff matrix for three-player PD game as following: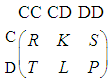 | (2) |
Where T > R > L > K > P > S should be satisfied [19]. And according to the outcome of choices for the players we have the following payoff vectors for players X, Y and Z respectively. S1 = (R, K, K, S, T, L, L, P), S2 = (R, K, T, L, K, S, L, P), S3 = (R, T, K, L, K, L, S, P).
2. Zero-Determinate Strategy for Three-Player IPDG
In this section, the focus is on determining the payoff of players when using ZD strategies.
2.1. The Transition Matrix for Three-player IPDG
For three-player, impose X player uses E strategy, Y player uses F strategy, and Z player uses G strategy. Accordingly, the transition matrix from one state to another M=(m)i,j can be obtained as following [16].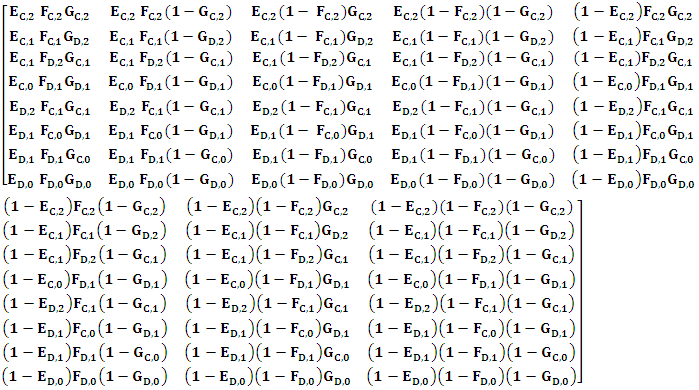 | (3) |
For example, to illustrate the previous matrix symbols, the element m4,5 denoting the probability of moving from the previous state CDD, to the current state DCC. Keeping in mind players X, Y and Z always select C in the current state. Because M has a unit eigenvalue, the matrix M՜ = M-I is singular, with zero determinant. Then the stationary vector V of the Markov matrix, or any vector proportional to it, satisfies [13]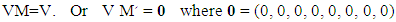 | (4) |
Applying Cramer’s rule to M՜ With det (M՜) =0, we get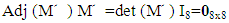 | (5) |
Where adj 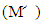 denote the adjunct matrix of
denote the adjunct matrix of 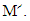 For the Markov chain with unique limiting distribution where the solution of the equation V M՜ = 0 (or V M = V) is unique up to a scalar factor [21,22]. That means that the solution of V M՜ = 0 is one dimensional since M՜ is 8x8 matrix with rank (M՜) = 7. Therefore adj (M՜) must be nonzero matrix. Without loss of generality we may assume that the eighth row of adj (M՜) is nonzero. Equations (4), (5) implies that every row of adj(M՜) is proportional to V. Choosing the eighth row, we see that the component of V is 7x7 matrices formed from the first seven columns of M՜. The determinant of M՜ is unchanged after some elementary column operations on matrix M՜. Now, a formula for the dot product of the limiting distribution vector V with an arbitrary eight-dimensional vector k = (k1, k2, k3, k4, k5, k6, k7, k8) is V. k ≡ D (E, F, G, k) Where D is the 8x8 determinate. f = D (E, F, G, k) =Det
For the Markov chain with unique limiting distribution where the solution of the equation V M՜ = 0 (or V M = V) is unique up to a scalar factor [21,22]. That means that the solution of V M՜ = 0 is one dimensional since M՜ is 8x8 matrix with rank (M՜) = 7. Therefore adj (M՜) must be nonzero matrix. Without loss of generality we may assume that the eighth row of adj (M՜) is nonzero. Equations (4), (5) implies that every row of adj(M՜) is proportional to V. Choosing the eighth row, we see that the component of V is 7x7 matrices formed from the first seven columns of M՜. The determinant of M՜ is unchanged after some elementary column operations on matrix M՜. Now, a formula for the dot product of the limiting distribution vector V with an arbitrary eight-dimensional vector k = (k1, k2, k3, k4, k5, k6, k7, k8) is V. k ≡ D (E, F, G, k) Where D is the 8x8 determinate. f = D (E, F, G, k) =Det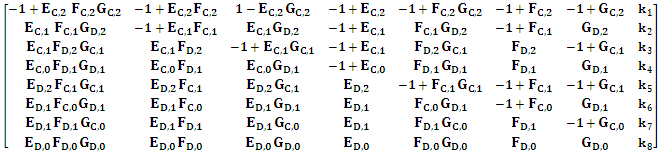 | (6) |
This result is very interesting because the determinate (E, F, G, k) has a special feature: its fourth column: 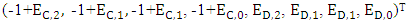 is solely under the control of X player. Its sixth column:
is solely under the control of X player. Its sixth column: 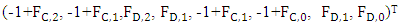 is solely under the control of Y player. Its seventh column:
is solely under the control of Y player. Its seventh column: 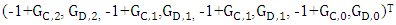 is solely under the control of Z player. We denote the transpose of fourth, sixth and seventh columns by
is solely under the control of Z player. We denote the transpose of fourth, sixth and seventh columns by 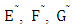 respectively.
respectively.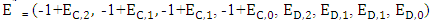 | (7) |
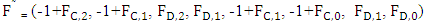 | (8) |
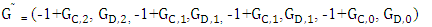 | (9) |
Then in the stationary state, the expected scores for players X, Y and Z respectively. 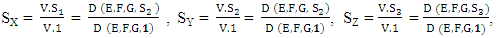 | (10) |
Where 1= (1, 1, 1, 1, 1, 1, 1, 1). Because the scores in (10) depends linearly on the expected payoff vector of each player. Then, we can perform linear combination of the expected payoffs of the three players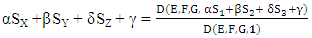 | (11) |
Now, equation (11) allows much control of the game by the players. Because players X, Y, and Z have the same possibility of choosing unilateral strategies that will make the determinant in the numerators vanish. That is, if X choose a strategy that satisfies 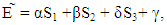 or if Y choose a strategy that satisfies
or if Y choose a strategy that satisfies 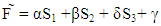 or if Z choose a strategy that satisfies
or if Z choose a strategy that satisfies 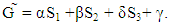 Then the determinate vanishes and a linear relation between the three scores became
Then the determinate vanishes and a linear relation between the three scores became 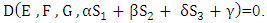 So that the linear relation
So that the linear relation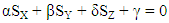 | (12) |
will be enforced. And this is called Zero-determinate ZD strategies.Note: Since 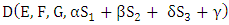 has its fourth column fully controlled by X player, so if X choosing strategy satisfying
has its fourth column fully controlled by X player, so if X choosing strategy satisfying 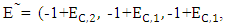
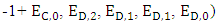
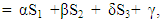 then the fourth column and eighth column of the
then the fourth column and eighth column of the 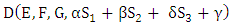 will be identical,
will be identical, 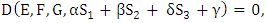 and
and 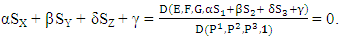
3. The Outcomes When One Player Using ZD Strategies
In this part the results of ZD strategies will be presented also, some kinds of ZD strategies which mentioned in press and Dyson paper will be studied.i. A player using ZD strategies can unilaterally set the opponent’s expected payoff to a value within a certain range.ii. A player using ZD strategies may tries to set his own expected payoff but it will fail. iii. A player using ZD strategies can demand a large share of the total payoffs over the mutual defection value, in this case ZD strategies are called, according to press and Dyson, extortionate strategies.Suppose an X-player is using ZD strategies and the strategy analysis will be applied to the X player.
3.1. X Unilaterally Set’s Y’s and Z’s Scores
One specialization of ZD strategies allows X to unilaterally set Y’s and Z’s scores. Where X needs only to play a fixed strategy satisfying 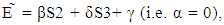 which depends on the strategy of the X-player and independent on the strategy of both players Y and Z. Then the desired strategy is:
which depends on the strategy of the X-player and independent on the strategy of both players Y and Z. Then the desired strategy is: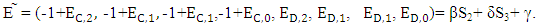 That is implies to
That is implies to 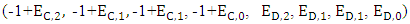
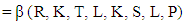
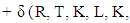
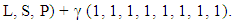 Then
Then 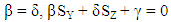 and the expected score for X player is
and the expected score for X player is 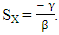 The following can be observed The six equations with six independent variables that can solve for
The following can be observed The six equations with six independent variables that can solve for 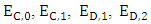 in terms of
in terms of 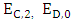 "mutual cooperation and mutual defection". Then from the two equations of mutual cooperation and mutual defection we can get the allowed values range of
"mutual cooperation and mutual defection". Then from the two equations of mutual cooperation and mutual defection we can get the allowed values range of 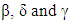 as follows:
as follows: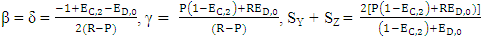 Thus, SY + SZ are actually a weighted average of double mutual defection payoff (2P) and mutual cooperation payoff (2R). Since
Thus, SY + SZ are actually a weighted average of double mutual defection payoff (2P) and mutual cooperation payoff (2R). Since 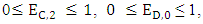 the range of expected payoff values of Y’s and Z’s can be determined unilaterally by X in the range from 2R and 2P. Then ifi.
the range of expected payoff values of Y’s and Z’s can be determined unilaterally by X in the range from 2R and 2P. Then ifi. 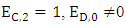 then, SY + SZ = 2Rii.
then, SY + SZ = 2Rii. 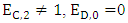 then, SY + SZ = 2PWe must have
then, SY + SZ = 2PWe must have 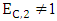 or,
or, 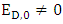 to calculate SY + SZ. Because If
to calculate SY + SZ. Because If 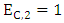 and,
and, 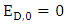 then the strategy for X player is
then the strategy for X player is 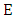 = (1, 1, 1, 1, 0, 0, 0, 0) is not valid strategy.
= (1, 1, 1, 1, 0, 0, 0, 0) is not valid strategy.
3.2. X Tries to Set Her Own Score
If X Tries to set his expected payoff, then set 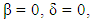 in
in 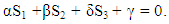 Thus
Thus 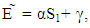 and
and 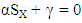 Which leads to the expected score for X player is
Which leads to the expected score for X player is 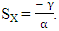 Then
Then 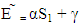 implies to
implies to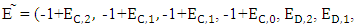
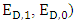
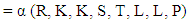
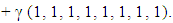 Then,
Then, 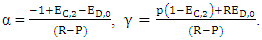 After the mathematical calculations can be obtained in the final form of the strategy of the player X
After the mathematical calculations can be obtained in the final form of the strategy of the player X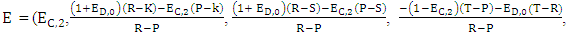
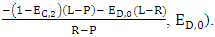 Obviously from strategy of player X,
Obviously from strategy of player X, 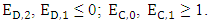 Hence the only one feasible solution is P = (1, 1, 1, 1, 0, 0, 0, 0), if X uses this strategy the fourth column of M՜ have all elements to be zero. Therefore, X cannot unilaterally set its own score.
Hence the only one feasible solution is P = (1, 1, 1, 1, 0, 0, 0, 0), if X uses this strategy the fourth column of M՜ have all elements to be zero. Therefore, X cannot unilaterally set its own score.
3.3. X Demands and Extortionate Share
It is possible to ask what might happen if X tries to enforce an extortionate share of payoffs to ensure a greater payoff? To answer this question will expresses the linear relation 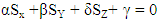 using another form
using another form 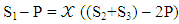 | (13) |
Where 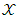 is called extortionate factor. By multiplying both sides of (13) by nonzero parameter
is called extortionate factor. By multiplying both sides of (13) by nonzero parameter 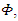 that used to ensure the feasibility of the strategy, then
that used to ensure the feasibility of the strategy, then 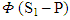
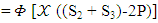
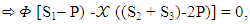 X need to choose a strategy satisfying
X need to choose a strategy satisfying 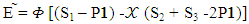 | (14) |
It’s implies to 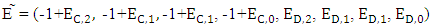
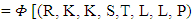
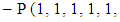
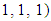
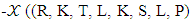
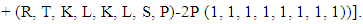 Then after the mathematical calculations can be obtained in the final form of the strategy of the player X.
Then after the mathematical calculations can be obtained in the final form of the strategy of the player X. 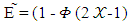
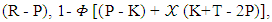
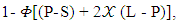
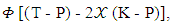
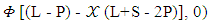 that is called extortionate strategy. Taking into account that the range value of
that is called extortionate strategy. Taking into account that the range value of 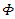 and
and 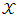 must be determined to achieve that
must be determined to achieve that 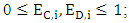 i = 0, 1, 2. Alex will study in the following cases.The case
i = 0, 1, 2. Alex will study in the following cases.The case 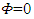 is formally allowed but produces only the singular strategy (1, 1, 1, 1, 0, 0, 0, 0). While The case
is formally allowed but produces only the singular strategy (1, 1, 1, 1, 0, 0, 0, 0). While The case 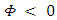 leading to
leading to 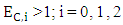 which is not valid strategy. Thus, it is required that
which is not valid strategy. Thus, it is required that 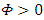 . It’s clear that, feasible strategy exists for allowed range of
. It’s clear that, feasible strategy exists for allowed range of 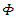
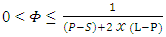 | (15) |
Now the values of the 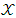 should be determined where it is realized that
should be determined where it is realized that 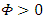 .
.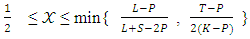 | (16) |
From (16) can be observed 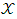 is different from IPD for two players where
is different from IPD for two players where 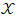 can take any value. According to (14) it is clear that the payoff of X player depends on the strategy of players Y, and Z. In which if both the Y and Z players use the all c strategy F = (1, 1, 1, 1, 1, 1, 1, 1), G = (1, 1, 1, 1, 1, 1, 1, 1), The player X will get bigger scores than if any one of the other players played defective. So, if X player uses the extortionate strategy and the other two players plays all C Strategy then the scores of players X, Y, and Z will maximize, in this case the X player scores will be greater than the other two players themselves. Therefore, X’s, Y’s, and Z’s maximum payoff when facing an extortionate player are given by.
can take any value. According to (14) it is clear that the payoff of X player depends on the strategy of players Y, and Z. In which if both the Y and Z players use the all c strategy F = (1, 1, 1, 1, 1, 1, 1, 1), G = (1, 1, 1, 1, 1, 1, 1, 1), The player X will get bigger scores than if any one of the other players played defective. So, if X player uses the extortionate strategy and the other two players plays all C Strategy then the scores of players X, Y, and Z will maximize, in this case the X player scores will be greater than the other two players themselves. Therefore, X’s, Y’s, and Z’s maximum payoff when facing an extortionate player are given by. | (17) |
example 3.1From Axelord’s payoff values we consider (T, R, L, K, P, S) = (5, 4, 3, 2, 1, 0) where T > R > L > K > P > S. In this casethe range of 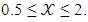 If X player using:i. 𝒳 =0.5, this gives 𝛷=0.33, SX = 9.33, SY = SZ = 4.ii. 𝒳 =2. Then 𝛷=0.2, SX =11, SY = SZ =2.8.Iii. 𝒳 =2. Then 𝛷=0.11, SX = 12.11, SY = SZ = 2.
If X player using:i. 𝒳 =0.5, this gives 𝛷=0.33, SX = 9.33, SY = SZ = 4.ii. 𝒳 =2. Then 𝛷=0.2, SX =11, SY = SZ =2.8.Iii. 𝒳 =2. Then 𝛷=0.11, SX = 12.11, SY = SZ = 2.
4. Conclusions
The following results were obtained when the X player used ZD strategies:i. In a unilaterally way, the player X can determine for its opponent a certain payoff if using strategy satisfying 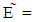
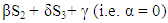 and Calculations have shown that this payoff ranges from 2P and 2R. ii. If X player trying to use a ZD strategies to set his expected payoff by using strategy. Satisfying
and Calculations have shown that this payoff ranges from 2P and 2R. ii. If X player trying to use a ZD strategies to set his expected payoff by using strategy. Satisfying 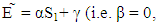
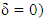 he will be disappointed. Because his technique leading to one possible strategy (1,1,1,1,0,0,0,0) which is not valid strategy, it leads to that the matrix
he will be disappointed. Because his technique leading to one possible strategy (1,1,1,1,0,0,0,0) which is not valid strategy, it leads to that the matrix 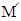 equal to zero. Then X can't be able to set his expected payoff.iii. Finally, X player can enforce a linear relationship to obtain an extortionate strategy and guaranteed a greater payoff than its opponents by using a strategy satisfying
equal to zero. Then X can't be able to set his expected payoff.iii. Finally, X player can enforce a linear relationship to obtain an extortionate strategy and guaranteed a greater payoff than its opponents by using a strategy satisfying 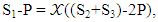 choosing a suitable range for both
choosing a suitable range for both 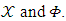 Where
Where 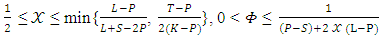 should be satisfied. The payoff to player X is far greater than the payoff earned by each other player of his opponents and this is thanks to its use of extortion strategy. In the future, we are looking for the possibility of using X player for ZD strategies and trying to help one of its opponents to get a bigger payoff than another player or Try to apply ZD strategies on a number of actions more than just two actions.
should be satisfied. The payoff to player X is far greater than the payoff earned by each other player of his opponents and this is thanks to its use of extortion strategy. In the future, we are looking for the possibility of using X player for ZD strategies and trying to help one of its opponents to get a bigger payoff than another player or Try to apply ZD strategies on a number of actions more than just two actions.
References
| [1] | John Von Neumann and Oskar Morgenstern: Theory of Games and Economic Behavior (1994). |
| [2] | John F Nash, (1950). Equilibrium points in n-person games. Proceedings of the National Academy of Sciences of the United States of America, Vol. 36, No. 1. (Jan. 15, 1950), pp. 48-49. |
| [3] | Nicolae, A., Gheorghe, S., (2012). How Contemporary Stays the Prisoner’s Dilemma in Economics? Romanian Statistical Review Supplement, 60(2): 23-28. |
| [4] | James W Friedman.yGame Theory with Applications to Economics, Oxford university press, New York, 1986. |
| [5] | Snyder, G.H., (1971). "Prisoner's Dilemma" and" Chicken" Models in International Politics. International Studies Quarterly, 15(1): 66-103. |
| [6] | Chen, X., Fu, F., Wang, L., (2007). Prisoner's Dilemma on Community Networks. Physica A: Statistical Mechanics and Its Applications. |
| [7] | PETER HAMMERSTEIN, REINHARD SELTEN. GAME THEORY AND EVOLUTIONARY BIOLOGY. Handbook of Game Theory, Volume 2. Elsevier Science B.V., 1994 (929-993). |
| [8] | Joseph Y. Halpern (2007). Computer Science and Game Theory: A Brief Survey. Cornell University. |
| [9] | M. Shahrabi Farahani, M. Sheikhmohammady. A review on symmetric games: theory, comparison and applications. International Journal of Applied Operational Research. Vol. 4, No. 3, pp. 91-106, Summer 2014. |
| [10] | William Poundstone (1922). Prisoner’s Dilemma. A Division of Random House, New York. |
| [11] | Abdellah Salhi, Hugh Glaser, David De Roure and John Putney (1996). The Prisoners' Dilemma Revisited. |
| [12] | Martin A. Nowak, Karl Sigmund, Esam El-Sedy. Automata, repeated games and noise. Journal of mathematical biology. springer 1995. |
| [13] | William H. Press, And Freeman J. Dyson. Iterated Prisoner’s Dilemma Contains Strategies That Dominate Any Evolutionary Opponent’s in Pnas (2012). |
| [14] | Ch. Hauert and H. G. Schuster (1997). Effects of Increasing the Number of Players and Memory Size in The Iterated Prisoner’s Dilemma: A Numerical Approach, A Numeric Approach. Proc Biol Sci 264:513:519. |
| [15] | JingChen, Aleksey Zinger. The robustness of zero-determinant strategies iIterated Prisoner׳s Dilemma games, Volume 357, Pages 46-54. |
| [16] | Liming Pan, Dong Hao, Zhigai Rong, and Tao Zhou. Zero-Determinate Strategies in The Iterated Public Goods Game, Scientific Reports Volume 5, Article Number: 13096 (2015). |
| [17] | Christian Hilbe, Martin A. Nowak, Arne Traulsen. Adaptive Dynamics of Extortion and Compliance. Matjaz Perc, University of Maribor, Slovenia. |
| [18] | Attila Szolnoki and Matjaž Perc. Evolution of extortion in structured populations. Phys. Rev. E 89, 022804. |
| [19] | Essam El-Seidy, Entisarat M. Elshobaky, And Karim M. Soliman. Two Population Three-Player Prisoner’s Dilemma Game. Applied Mathematics and Computation (2016), 277 44-53. |
| [20] | Essam El-Seidy, Karim.M. Soliman. Iterated symmetric three-player prisoner’s dilemma game. Applied Mathematics and Computation. |
| [21] | Mark A. Pinsky, Samuel Karlin. An Introduction to Stochastic Modeling, 4th Edition Academic Press. |
| [22] | David A. Levin, Yuval Peres, Elizabeth L. Wilmer. Markov Chains and Mixing Times American Mathematical Society. |



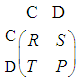
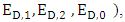 Y’s strategy by the vector
Y’s strategy by the vector 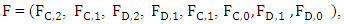 and Z’s strategy by the vector
and Z’s strategy by the vector 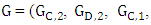
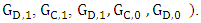 The possibility of cooperation can be denoted by
The possibility of cooperation can be denoted by 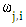 : j denotes player
: j denotes player 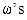 previous move and i represents the number of cooperating of
previous move and i represents the number of cooperating of 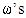 opponents in the previous round,
opponents in the previous round, 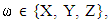
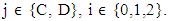 For example, if
For example, if 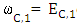 denote the probability that X player play cooperate after the outcome CDC or CCD in the previous round, and
denote the probability that X player play cooperate after the outcome CDC or CCD in the previous round, and 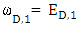 denote the probability that X player play cooperate after the outcome DCD or DDC in the previous round, this point of view applies for each player.
denote the probability that X player play cooperate after the outcome DCD or DDC in the previous round, this point of view applies for each player.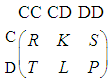
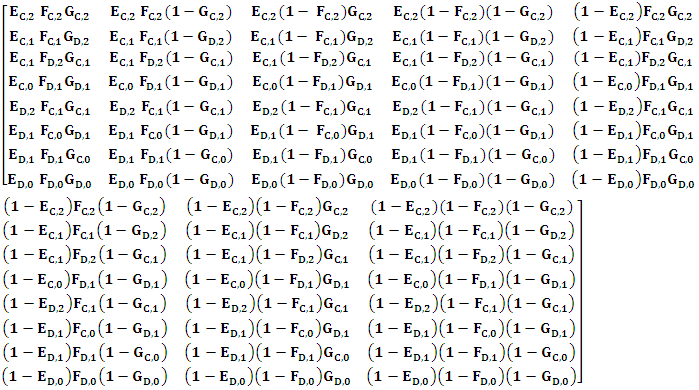
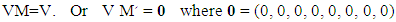
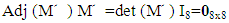
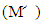 denote the adjunct matrix of
denote the adjunct matrix of  For the Markov chain with unique limiting distribution where the solution of the equation V M՜ = 0 (or V M = V) is unique up to a scalar factor [21,22]. That means that the solution of V M՜ = 0 is one dimensional since M՜ is 8x8 matrix with rank (M՜) = 7. Therefore adj (M՜) must be nonzero matrix. Without loss of generality we may assume that the eighth row of adj (M՜) is nonzero. Equations (4), (5) implies that every row of adj(M՜) is proportional to V. Choosing the eighth row, we see that the component of V is 7x7 matrices formed from the first seven columns of M՜. The determinant of M՜ is unchanged after some elementary column operations on matrix M՜. Now, a formula for the dot product of the limiting distribution vector V with an arbitrary eight-dimensional vector k = (k1, k2, k3, k4, k5, k6, k7, k8) is V. k ≡ D (E, F, G, k) Where D is the 8x8 determinate. f = D (E, F, G, k) =Det
For the Markov chain with unique limiting distribution where the solution of the equation V M՜ = 0 (or V M = V) is unique up to a scalar factor [21,22]. That means that the solution of V M՜ = 0 is one dimensional since M՜ is 8x8 matrix with rank (M՜) = 7. Therefore adj (M՜) must be nonzero matrix. Without loss of generality we may assume that the eighth row of adj (M՜) is nonzero. Equations (4), (5) implies that every row of adj(M՜) is proportional to V. Choosing the eighth row, we see that the component of V is 7x7 matrices formed from the first seven columns of M՜. The determinant of M՜ is unchanged after some elementary column operations on matrix M՜. Now, a formula for the dot product of the limiting distribution vector V with an arbitrary eight-dimensional vector k = (k1, k2, k3, k4, k5, k6, k7, k8) is V. k ≡ D (E, F, G, k) Where D is the 8x8 determinate. f = D (E, F, G, k) =Det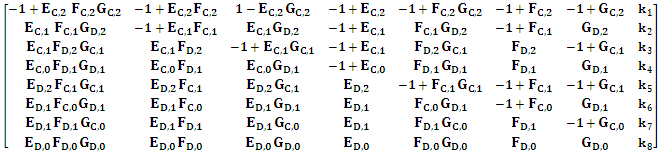
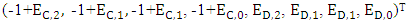 is solely under the control of X player. Its sixth column:
is solely under the control of X player. Its sixth column: 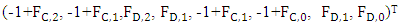 is solely under the control of Y player. Its seventh column:
is solely under the control of Y player. Its seventh column: 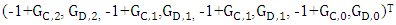 is solely under the control of Z player. We denote the transpose of fourth, sixth and seventh columns by
is solely under the control of Z player. We denote the transpose of fourth, sixth and seventh columns by 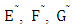 respectively.
respectively.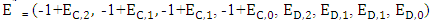
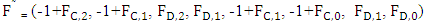
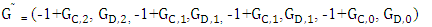
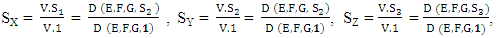
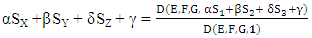
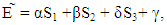 or if Y choose a strategy that satisfies
or if Y choose a strategy that satisfies 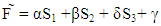 or if Z choose a strategy that satisfies
or if Z choose a strategy that satisfies 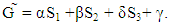 Then the determinate vanishes and a linear relation between the three scores became
Then the determinate vanishes and a linear relation between the three scores became 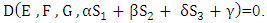 So that the linear relation
So that the linear relation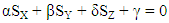
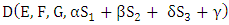 has its fourth column fully controlled by X player, so if X choosing strategy satisfying
has its fourth column fully controlled by X player, so if X choosing strategy satisfying 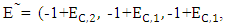
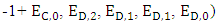
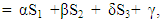 then the fourth column and eighth column of the
then the fourth column and eighth column of the 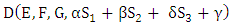 will be identical,
will be identical, 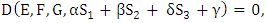 and
and 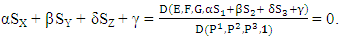
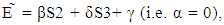 which depends on the strategy of the X-player and independent on the strategy of both players Y and Z. Then the desired strategy is:
which depends on the strategy of the X-player and independent on the strategy of both players Y and Z. Then the desired strategy is: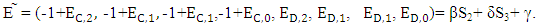 That is implies to
That is implies to 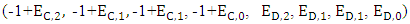
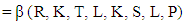
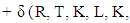
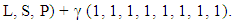 Then
Then 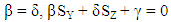 and the expected score for X player is
and the expected score for X player is 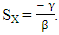 The following can be observed The six equations with six independent variables that can solve for
The following can be observed The six equations with six independent variables that can solve for 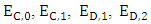 in terms of
in terms of 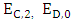 "mutual cooperation and mutual defection". Then from the two equations of mutual cooperation and mutual defection we can get the allowed values range of
"mutual cooperation and mutual defection". Then from the two equations of mutual cooperation and mutual defection we can get the allowed values range of 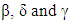 as follows:
as follows: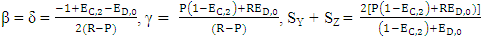 Thus, SY + SZ are actually a weighted average of double mutual defection payoff (2P) and mutual cooperation payoff (2R). Since
Thus, SY + SZ are actually a weighted average of double mutual defection payoff (2P) and mutual cooperation payoff (2R). Since 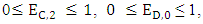 the range of expected payoff values of Y’s and Z’s can be determined unilaterally by X in the range from 2R and 2P. Then ifi.
the range of expected payoff values of Y’s and Z’s can be determined unilaterally by X in the range from 2R and 2P. Then ifi. 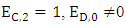 then, SY + SZ = 2Rii.
then, SY + SZ = 2Rii. 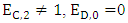 then, SY + SZ = 2PWe must have
then, SY + SZ = 2PWe must have 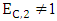 or,
or, 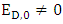 to calculate SY + SZ. Because If
to calculate SY + SZ. Because If 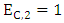 and,
and, 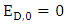 then the strategy for X player is
then the strategy for X player is 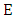 = (1, 1, 1, 1, 0, 0, 0, 0) is not valid strategy.
= (1, 1, 1, 1, 0, 0, 0, 0) is not valid strategy.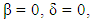 in
in 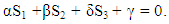 Thus
Thus 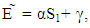 and
and 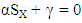 Which leads to the expected score for X player is
Which leads to the expected score for X player is 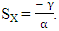 Then
Then 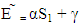 implies to
implies to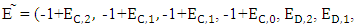
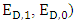
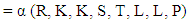
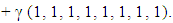 Then,
Then, 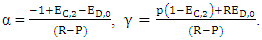 After the mathematical calculations can be obtained in the final form of the strategy of the player X
After the mathematical calculations can be obtained in the final form of the strategy of the player X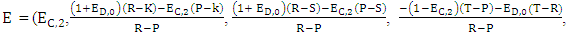
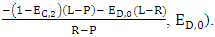 Obviously from strategy of player X,
Obviously from strategy of player X, 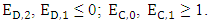 Hence the only one feasible solution is P = (1, 1, 1, 1, 0, 0, 0, 0), if X uses this strategy the fourth column of M՜ have all elements to be zero. Therefore, X cannot unilaterally set its own score.
Hence the only one feasible solution is P = (1, 1, 1, 1, 0, 0, 0, 0), if X uses this strategy the fourth column of M՜ have all elements to be zero. Therefore, X cannot unilaterally set its own score. 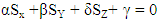 using another form
using another form 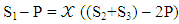
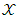 is called extortionate factor. By multiplying both sides of (13) by nonzero parameter
is called extortionate factor. By multiplying both sides of (13) by nonzero parameter 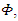 that used to ensure the feasibility of the strategy, then
that used to ensure the feasibility of the strategy, then 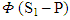
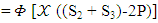
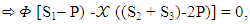 X need to choose a strategy satisfying
X need to choose a strategy satisfying 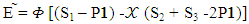
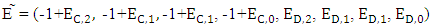
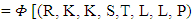
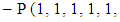
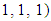
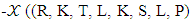
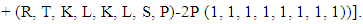 Then after the mathematical calculations can be obtained in the final form of the strategy of the player X.
Then after the mathematical calculations can be obtained in the final form of the strategy of the player X. 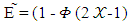
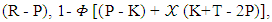
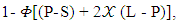
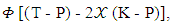
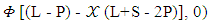 that is called extortionate strategy. Taking into account that the range value of
that is called extortionate strategy. Taking into account that the range value of 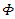 and
and 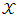 must be determined to achieve that
must be determined to achieve that 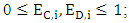 i = 0, 1, 2. Alex will study in the following cases.The case
i = 0, 1, 2. Alex will study in the following cases.The case 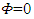 is formally allowed but produces only the singular strategy (1, 1, 1, 1, 0, 0, 0, 0). While The case
is formally allowed but produces only the singular strategy (1, 1, 1, 1, 0, 0, 0, 0). While The case 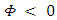 leading to
leading to 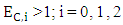 which is not valid strategy. Thus, it is required that
which is not valid strategy. Thus, it is required that 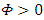 . It’s clear that, feasible strategy exists for allowed range of
. It’s clear that, feasible strategy exists for allowed range of 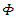
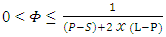
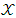 should be determined where it is realized that
should be determined where it is realized that 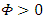 .
.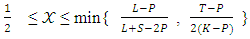
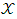 is different from IPD for two players where
is different from IPD for two players where 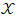 can take any value. According to (14) it is clear that the payoff of X player depends on the strategy of players Y, and Z. In which if both the Y and Z players use the all c strategy F = (1, 1, 1, 1, 1, 1, 1, 1), G = (1, 1, 1, 1, 1, 1, 1, 1), The player X will get bigger scores than if any one of the other players played defective. So, if X player uses the extortionate strategy and the other two players plays all C Strategy then the scores of players X, Y, and Z will maximize, in this case the X player scores will be greater than the other two players themselves. Therefore, X’s, Y’s, and Z’s maximum payoff when facing an extortionate player are given by.
can take any value. According to (14) it is clear that the payoff of X player depends on the strategy of players Y, and Z. In which if both the Y and Z players use the all c strategy F = (1, 1, 1, 1, 1, 1, 1, 1), G = (1, 1, 1, 1, 1, 1, 1, 1), The player X will get bigger scores than if any one of the other players played defective. So, if X player uses the extortionate strategy and the other two players plays all C Strategy then the scores of players X, Y, and Z will maximize, in this case the X player scores will be greater than the other two players themselves. Therefore, X’s, Y’s, and Z’s maximum payoff when facing an extortionate player are given by.
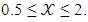 If X player using:i. 𝒳 =0.5, this gives 𝛷=0.33, SX = 9.33, SY = SZ = 4.ii. 𝒳 =2. Then 𝛷=0.2, SX =11, SY = SZ =2.8.Iii. 𝒳 =2. Then 𝛷=0.11, SX = 12.11, SY = SZ = 2.
If X player using:i. 𝒳 =0.5, this gives 𝛷=0.33, SX = 9.33, SY = SZ = 4.ii. 𝒳 =2. Then 𝛷=0.2, SX =11, SY = SZ =2.8.Iii. 𝒳 =2. Then 𝛷=0.11, SX = 12.11, SY = SZ = 2.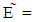
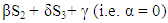 and Calculations have shown that this payoff ranges from 2P and 2R. ii. If X player trying to use a ZD strategies to set his expected payoff by using strategy. Satisfying
and Calculations have shown that this payoff ranges from 2P and 2R. ii. If X player trying to use a ZD strategies to set his expected payoff by using strategy. Satisfying 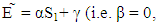
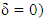 he will be disappointed. Because his technique leading to one possible strategy (1,1,1,1,0,0,0,0) which is not valid strategy, it leads to that the matrix
he will be disappointed. Because his technique leading to one possible strategy (1,1,1,1,0,0,0,0) which is not valid strategy, it leads to that the matrix 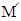 equal to zero. Then X can't be able to set his expected payoff.iii. Finally, X player can enforce a linear relationship to obtain an extortionate strategy and guaranteed a greater payoff than its opponents by using a strategy satisfying
equal to zero. Then X can't be able to set his expected payoff.iii. Finally, X player can enforce a linear relationship to obtain an extortionate strategy and guaranteed a greater payoff than its opponents by using a strategy satisfying 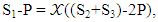 choosing a suitable range for both
choosing a suitable range for both 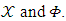 Where
Where 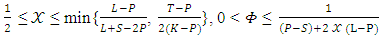 should be satisfied. The payoff to player X is far greater than the payoff earned by each other player of his opponents and this is thanks to its use of extortion strategy. In the future, we are looking for the possibility of using X player for ZD strategies and trying to help one of its opponents to get a bigger payoff than another player or Try to apply ZD strategies on a number of actions more than just two actions.
should be satisfied. The payoff to player X is far greater than the payoff earned by each other player of his opponents and this is thanks to its use of extortion strategy. In the future, we are looking for the possibility of using X player for ZD strategies and trying to help one of its opponents to get a bigger payoff than another player or Try to apply ZD strategies on a number of actions more than just two actions.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML