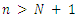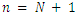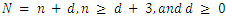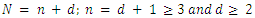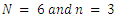-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2019; 8(2): 25-31
doi:10.5923/j.jgt.20190802.01

Algorithm for Multilple Player Last Nim for Any Alliance System
Essam El_Seidy, Hassan El Kady, Dieaa I. Nassr
Department of Mathematics, Faculty of Science, Ain Shams University, Egypt
Correspondence to: Essam El_Seidy, Department of Mathematics, Faculty of Science, Ain Shams University, Egypt.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The Last Nim game is an impartial combinatorial game studied only in the case of the standard alliance matrix. In this paper, we consider the Last Nim game with N linearly ordered nonempty piles containing counters, and n players for any alliance matrix. For this, we give an algorithm to get the winner, the tree of all possibilities of the game, and the best strategy for the winner. For the practical result, we implement this algorithm using C++ language and give some examples.
Keywords: Game Theory, Combinatorial game, Nim Game and MLNim(N,n)
Cite this paper: Essam El_Seidy, Hassan El Kady, Dieaa I. Nassr, Algorithm for Multilple Player Last Nim for Any Alliance System, Journal of Game Theory, Vol. 8 No. 2, 2019, pp. 25-31. doi: 10.5923/j.jgt.20190802.01.
Article Outline
1. Introduction
- Combinatorial game theory is an important branch of game theory and a pure strategy game with no chance. It is played by two or more players who play alternately, they can move to a finite number of positions. All players have a complete knowledge of the game, such as Hackenbuch, Chess, Tic Tac Toe and Nim. W.A.Liu and J.Yang [1] introduced the multi-player last Nim when the standard alliance matrix is adopted.E.El-Seidy, S.E.S.Hussein and A.T.Alabdala [2], that is, the combinatorial game is with perfect information. The determination of the winner in the combinatorial game is based on normal play or misere play. In the normal game, the player who makes the last legal move wins, while in the misere play, the player making the last legal move makes the next player the winner. There are two main types of combinatorial play, impartial play and partizan play. In the impartial game, all players have the same option and the same position. e.g., Nim and Hachenbuch . In the game of partizan, each player has a different position that can move and all players play according to the same rules. e.g., Chess and Tic Tac Toe. The Nim game is an impartial game played alternately by two players. The game is a set of piles where these piles are ordered linearly and in each pile a number of counters. The player step is taken by removing any number of piles from any pile. Nim game is introduced by Bouton [3], Albert MH and Nowakowski [4], Flammenkamp et al. [5], Holshouser et. al. [6], Liu and Zhao [7]. There are many types for the Nim games, We conclude these results as follows:• Circular Nim, this game was introduced by Matthieu Dufour and Silvia [8] is an impartial combinatorial game consisting of several piles of counters placed in a circle. The player chooses m consecutive piles. The player removes at least one counter from one or more piles of the m consecutive piles. The player who makes the last move wins.• The Classical Game of Fibonacci Nim, this game was introduced by Michael J. Whinihan [9], there is a pile of n stones (counters) and players make moves by removing stones under certain constraints. A player must remove at least one stone from the pile and if a player removes m stones, the next player should remove at most 2m stones. The first player cannot remove all the stones.• Nim on Graph by M. Fukuyama [10] is an impartial game played by two players. It contains an undirected graph in which each edge is assigned to a positive integer. To start the game, place an indicator at a vertex called the starting position. Both players take turns and the move can be summarized as follows: Choose an edge incident with the vertex containing the indicator piece. Decrease this edge to any strictly smaller non-negative integer. Move the piece to the adjacent vertex along this edge. If each edge incident with the piece has zero value, then the player to play is the loser and the game is over.• Small Nim game, this game was introduced by W.A.Liu and J.J. Zhou [11], in this game there are linearly ordered piles containing counters where a player makes a move by removing any number of counters in a pile of the smallest number of counters. The player who cannot make a move loses the game.• _ End Nim game, this game was introduced by Albert MH and Nowakowski RJ [12], there are two players called Left and Right and a vector (string) of nonempty piles containing counters. Both players take turns by removing one or more counters, the player on the left removing counters from the leftmost nonempty pile and the player on the right removing counters from the rightmost nonempty pile, unless do not stay a pile. The player who can not make a move loses.• Last Nim game, this game was introduced by Friedman E. [13], there are linearly ordered piles containing counters where a player takes his turn by removing any number of counters from the last pile. In the normal play, the player who makes the last move wins. While in misere play, the last player who cannot make a move wins.In recent years, games of two players have been the subject of a comprehensive study.These games are normal to be generalized to three players or even to
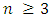 players to be called multiplayer games. In addition, multiplayer games are studied in different forms. For example, multi-player without alliance [14-18] multi-player with two alliances [19,20] and multi-players with a system of alliances [22,23].In this article, we give Algorithms 3.1, 3.2 and 3.3 to determine the game value function of the multi-player Last Nim game for any alliance matrix. In addition, the _rst move can be made by any player. i.e., it is not necessary for P0 to perform the first move. As a result, the game value function and the winner player are modified according to the player who makes the first move. Therefore, we denote the player who make the first move in our implementation by
players to be called multiplayer games. In addition, multiplayer games are studied in different forms. For example, multi-player without alliance [14-18] multi-player with two alliances [19,20] and multi-players with a system of alliances [22,23].In this article, we give Algorithms 3.1, 3.2 and 3.3 to determine the game value function of the multi-player Last Nim game for any alliance matrix. In addition, the _rst move can be made by any player. i.e., it is not necessary for P0 to perform the first move. As a result, the game value function and the winner player are modified according to the player who makes the first move. Therefore, we denote the player who make the first move in our implementation by 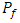 .The paper is organized as follows. In Sect 2, we give some basic concepts of the multi-player last Nim game. New Algorithms to compute the game value function of the Last multi-player last Nim game for any alliance matrix are presented in Sect 3. In Sect 4, we give the result of our implementation. Section 5 includes the conclusion.
.The paper is organized as follows. In Sect 2, we give some basic concepts of the multi-player last Nim game. New Algorithms to compute the game value function of the Last multi-player last Nim game for any alliance matrix are presented in Sect 3. In Sect 4, we give the result of our implementation. Section 5 includes the conclusion.2. Multi-player Last Nim with Alliance System
- The following definitions are to summarize the last Name with alliance alliance system [1, 22]Definition 2.1 (Multiple players Last Nim). Given linearly ordered N piles
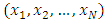 where each pile has counters. There are
where each pile has counters. There are 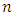 players who take turn by removing any number of counters from the last nonempty pile (containing at least one counter). If each pile has zero value, then the player to play is the winner and the game is over. We denote this game by
players who take turn by removing any number of counters from the last nonempty pile (containing at least one counter). If each pile has zero value, then the player to play is the winner and the game is over. We denote this game by 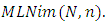 Definition 2.2 (Krawec [22, 23]). (i) Assume that the players are given by
Definition 2.2 (Krawec [22, 23]). (i) Assume that the players are given by 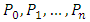 . The player
. The player 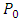 makes the first move followed by
makes the first move followed by 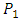 and so on. The Player
and so on. The Player 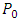 has to play again after
has to play again after 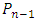 has played. i.e.,
has played. i.e., 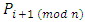 is
is 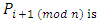 the next player after
the next player after 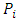 .(ii) For a game G with n players, the game value
.(ii) For a game G with n players, the game value 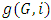 is a non-negative integer less than
is a non-negative integer less than 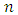 that specifes the winner in relation to the player pi. , that is, if
that specifes the winner in relation to the player pi. , that is, if 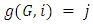 then the player
then the player 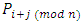 has a winning strategy.(iii) An endgame, denoted by _ is a game which has no legal move is available.(iv) The options of G, denoted by opt(G) is the set of all cases the current player can move to it.Definition 2.3. (i) For a game G with n players, an alliance matrix is an
has a winning strategy.(iii) An endgame, denoted by _ is a game which has no legal move is available.(iv) The options of G, denoted by opt(G) is the set of all cases the current player can move to it.Definition 2.3. (i) For a game G with n players, an alliance matrix is an 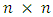 matrix which takes the form:
matrix which takes the form: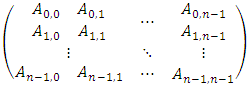 where
where 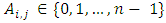 The row
The row 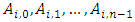 gives the linear order of priority of the desired winner relative to the player
gives the linear order of priority of the desired winner relative to the player 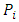 where the player
where the player 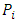 prefers the player
prefers the player 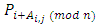 more than the player
more than the player 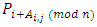 if
if 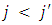 .(ii) The Standard Alliance Matrix, denoted by SAM in which
.(ii) The Standard Alliance Matrix, denoted by SAM in which 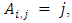 i.e., the player
i.e., the player 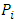 prefers player
prefers player 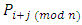 more than the player
more than the player 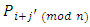 if
if 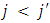 This matrix takes the following form:
This matrix takes the following form: Example 2.4.If
Example 2.4.If 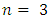 and
and  Definition 2.5 (The Game Value Function [22]). The game value function is given by
Definition 2.5 (The Game Value Function [22]). The game value function is given by 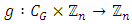 (where
(where 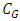 denotes the set of all impartial combinatorial games,
denotes the set of all impartial combinatorial games, 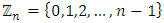 )
)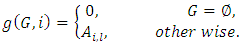 where:
where: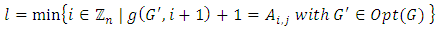 Wen An Liu and Juan Yang (2017) [1] generalized the game value function for any game position for
Wen An Liu and Juan Yang (2017) [1] generalized the game value function for any game position for 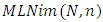 as a vector
as a vector 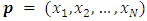 that can move in two ways. to it, which are
that can move in two ways. to it, which are 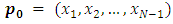 and
and 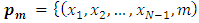
 therefore the game value function will take the following form:
therefore the game value function will take the following form: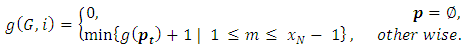
3. Algorithm
- In this section, we present algorithms that can be used to compute the game value function of the Last Nim multi-player game for any alliance matrix and the first move can be performed by any player. We describe the formate of game state in every move and then present Algorithms 3.1 and 3.2 to build the tree of all possible moves (cases) of the game recursively. After that, we use this tree as input for Algorithm 3.3 to compute the game value function. i.e., find the winner. Let the state of the game be described by the player who has the order to move and counters remaining in each pile during the game. We write the state as
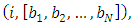 where
where 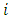 is the player number (
is the player number (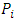 is the player to move), N is the number of piles and
is the player to move), N is the number of piles and 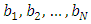 is a list of piles' counter.Algorithm 3.1.Input:
is a list of piles' counter.Algorithm 3.1.Input: 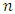 is the number of players, a list
is the number of players, a list 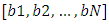 of piles' counter. i.e.
of piles' counter. i.e. 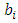 is the counter in the pile
is the counter in the pile 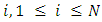 Output: tr is the tree of all possible cases of the game.Begin1.
Output: tr is the tree of all possible cases of the game.Begin1. 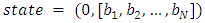 2. set state to be the root of tr3. call Algorithm 3.2 for the root state
2. set state to be the root of tr3. call Algorithm 3.2 for the root state 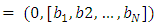 4. return trEndIn the following algorithm, we have the pile bi will be emptied before the pile
4. return trEndIn the following algorithm, we have the pile bi will be emptied before the pile 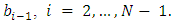 Algorithm 3.2.Input: n is the number of players, the current state = (k; [b1; b2; : : : ; bN]); where Pk is the current player and
Algorithm 3.2.Input: n is the number of players, the current state = (k; [b1; b2; : : : ; bN]); where Pk is the current player and 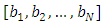 is a list of piles' counter.Output: recursively return the tree of all possible cases.Begin1. if game over then2. return3. end if4.
is a list of piles' counter.Output: recursively return the tree of all possible cases.Begin1. if game over then2. return3. end if4. 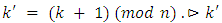 is the next player5.
is the next player5. 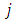 is the last nonempty pile.6. for
is the last nonempty pile.6. for 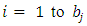 do7. append child
do7. append child 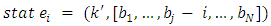 for the current state8. recursive call Algorithm 3.2 for the child
for the current state8. recursive call Algorithm 3.2 for the child 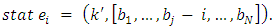 9. end forEndWe give Algorithm 3.3 to find the winner.Algorithm 3.3.Input: tr is the tree of all possible moves (cases) of the game, n is the number of players,M is the alliance matrix, root is the root of tr.Output: the winner of tr.Begin1. let
9. end forEndWe give Algorithm 3.3 to find the winner.Algorithm 3.3.Input: tr is the tree of all possible moves (cases) of the game, n is the number of players,M is the alliance matrix, root is the root of tr.Output: the winner of tr.Begin1. let 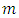 be the number of children of root2. if
be the number of children of root2. if 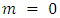 then3. return the winner is root4. end if5. define
then3. return the winner is root4. end if5. define 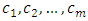 to be the children of root6. for
to be the children of root6. for 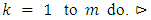 looping through children7. let trk be the subtree with root
looping through children7. let trk be the subtree with root 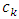 8. recursively call Algorithm 3.3 for the subtree
8. recursively call Algorithm 3.3 for the subtree 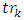 9. end for10. let rootId be the player in root11. for
9. end for10. let rootId be the player in root11. for 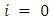 to
to 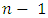 do.
do.  looping through players according priority12. for
looping through players according priority12. for 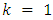 to
to 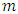 do.
do.  looping through winners of subtrees13. let
looping through winners of subtrees13. let 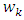 be the winner of
be the winner of 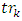 14. if
14. if 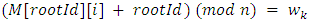 then15. return the winner state is
then15. return the winner state is 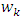 16. end if17. end for18. end forEnd
16. end if17. end for18. end forEnd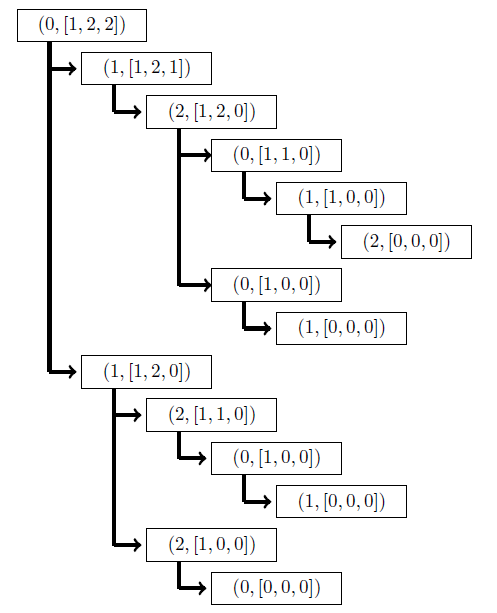 | Figure 1. Tree of All Possible Cases |
 In the case where 0 is the _rst player, we have the tree of all possible cases that is constructed, recursively, by Algorithms 3.1 and 3.2 as in Figure 1.The winner is the player 2; where the game steps are:
In the case where 0 is the _rst player, we have the tree of all possible cases that is constructed, recursively, by Algorithms 3.1 and 3.2 as in Figure 1.The winner is the player 2; where the game steps are: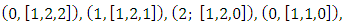
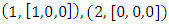
4. Implementation
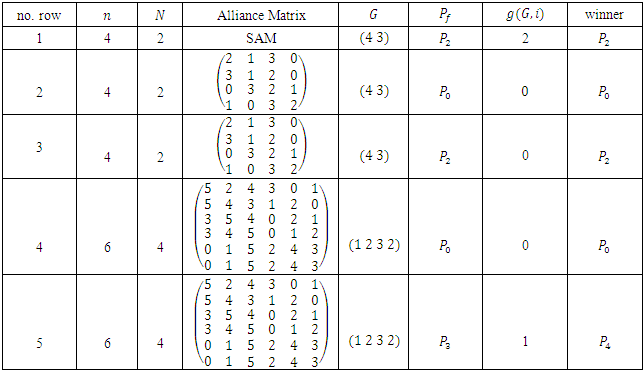
- We give a simple implementation of Algorithms 3.1, 3.2 and 3.3. The implementation was written in the C++ language. Our platform was Pentium IV 3.2 GHz with windows operating system, we present some results of our implementation for multiple players last Nim game with different cases of N (of piles) and n (of players). In addition, we have examples of last Nim game with different alliance matrices and we indicate that any change in the alliance matrix leads to a change in the game value function and the winner. The result can be summarized as the following:1. In table 1, we use our implementation to find the game value of multiple players last Nim with different alliance matrices in the case
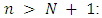 Accordingly, we confirm that the output of our implementation agree with the result of W.A.Liu and J.Yand [1] in the case of the standard alliance matrix.2. In table 2, we consider the case n = N +1; then we compute the game value function and the winner according to various alliance matrices. The outputs confirm the resultof W.A.Liu and J.Yang [1]. In this case, the result of W.A.Liu and J.Yang [1] gives the game value function equal to the number of piles if the last pile contains one counter and if the last pile contains several counters, it equals to zero., i.e.
Accordingly, we confirm that the output of our implementation agree with the result of W.A.Liu and J.Yand [1] in the case of the standard alliance matrix.2. In table 2, we consider the case n = N +1; then we compute the game value function and the winner according to various alliance matrices. The outputs confirm the resultof W.A.Liu and J.Yang [1]. In this case, the result of W.A.Liu and J.Yang [1] gives the game value function equal to the number of piles if the last pile contains one counter and if the last pile contains several counters, it equals to zero., i.e.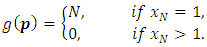 3. Wen An Liu and Juan Yang [1] studied the game value in the case of
3. Wen An Liu and Juan Yang [1] studied the game value in the case of 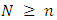 and defined the variable
and defined the variable 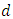 the difference between the number of piles and the number of players, i.e.
the difference between the number of piles and the number of players, i.e. 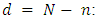 In this case, we denote the game by
In this case, we denote the game by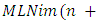
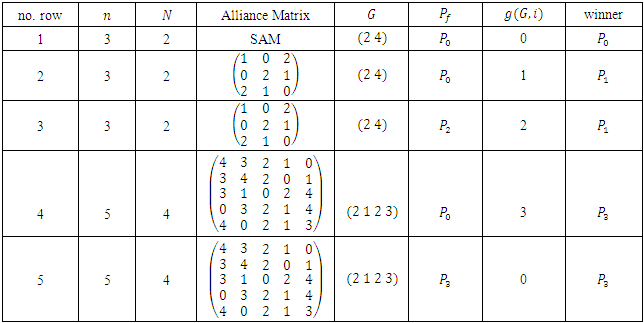
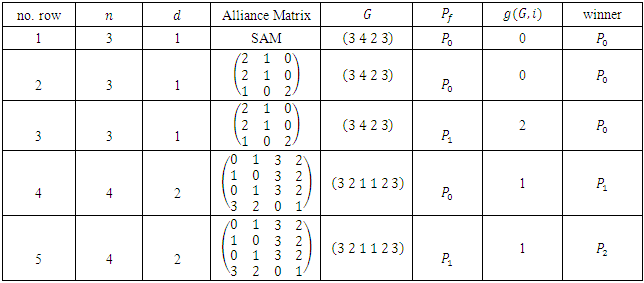
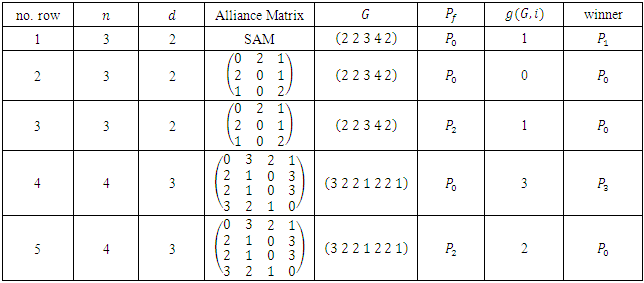
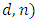 and give examples for various alliance matrices.(a) In table 3, we give the output of the implementation for
and give examples for various alliance matrices.(a) In table 3, we give the output of the implementation for 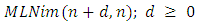 and
and 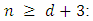 The output confirms the result of W.A.Liu and J.Yang [1], in this case, the game value is given by:
The output confirms the result of W.A.Liu and J.Yang [1], in this case, the game value is given by: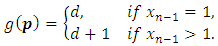 (b) In table 4, we give the output of the implementation for
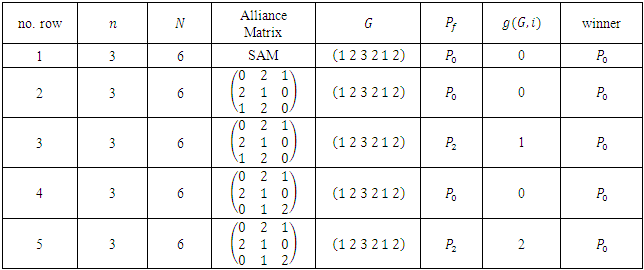
(b) In table 4, we give the output of the implementation for 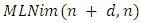 and
and 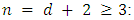 The output confirms the result of W.A.Liu and J.Yang [1], where in this case, the game value is given by:
The output confirms the result of W.A.Liu and J.Yang [1], where in this case, the game value is given by: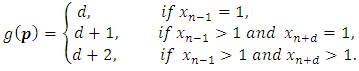 (c) In table 5, we give the output of the implementation for
(c) In table 5, we give the output of the implementation for 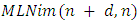 and
and 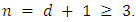 The output confirms the result of W.A.Liu and J.Yang [1], where in this case, the game value is given by:
The output confirms the result of W.A.Liu and J.Yang [1], where in this case, the game value is given by: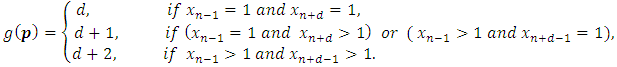 4. Wen An Liu and Juan Yang [1] give the game value function for
4. Wen An Liu and Juan Yang [1] give the game value function for 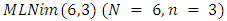 where the alliance matrix is the standard matrix by:
where the alliance matrix is the standard matrix by: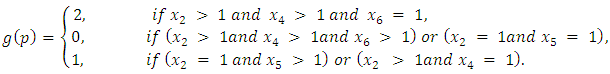
|
|
|
|
|
|
5. Conclusions
- In this paper, we proposed an algorithm for the latest Nim multi-player game with any alliance system. In [1], W.A.Liu and J.Yang have studied the game value function in the case of the standard alliance matrix with the number of piles N and the number of players
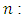 To the best of our knowledge, no results were taken into account with an alliance matrix different from the standard one. Therefore, the algorithm proposed in this article is the first attempt to calculate the game value function of the Last Nim multiplayer game for any alliance matrix. We implemented this algorithm in C ++ language. The entries for our implementation are the initial state of the Nim game, the alliance matrix, and the player making the first move. The outputs are the winning player, the tree of all possible moves of the game and the winning strategy to which the winning player must play. We also performed the implementation in the case of the standard alliance matrix in order to compare our result with those of W.A.Liu and J.Yang and we saw that the result is identical in the different cases of N and n.
To the best of our knowledge, no results were taken into account with an alliance matrix different from the standard one. Therefore, the algorithm proposed in this article is the first attempt to calculate the game value function of the Last Nim multiplayer game for any alliance matrix. We implemented this algorithm in C ++ language. The entries for our implementation are the initial state of the Nim game, the alliance matrix, and the player making the first move. The outputs are the winning player, the tree of all possible moves of the game and the winning strategy to which the winning player must play. We also performed the implementation in the case of the standard alliance matrix in order to compare our result with those of W.A.Liu and J.Yang and we saw that the result is identical in the different cases of N and n. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML