Yeremia Maroutian
11806 Miles Ave Apt. 112, Cleveland Oh. 44105, USA
Correspondence to: Yeremia Maroutian , 11806 Miles Ave Apt. 112, Cleveland Oh. 44105, USA.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper for fuzzy cooperative games we generalize the classical Shapley value through using one of the known approaches for its redefinition. For fuzzy cooperative games formalized as well the Shapley axioms. For the fuzzy pre-value of Shapley we research certain of known properties that hold true for classical Shapley value.
Keywords:
Fuzzy cooperative games, Fuzzy coalition, Fuzzy Shapley pre-value
Cite this paper: Yeremia Maroutian , The Shapley Pre-value for Fuzzy Cooperative Games, Journal of Game Theory, Vol. 8 No. 1, 2019, pp. 16-24. doi: 10.5923/j.jgt.20190801.03.
1. Introduction
The cooperative fuzzy games reflect type of situations in which for players allowed to take part in coalitions with participation levels that can vary from non-cooperation to full cooperation. Fuzzy coalitions describe levels of participation at which players involved in cooperation. The reward for players in this type of games defines depending on their level of cooperation.An important topic of research for fuzzy cooperative theory is the extension of existing in classical theory decision concepts on fuzzy games. It is known, that not every classical concept has its natural counterpart for fuzzy games. At the same time some results in classical theory allow to be transformed on fuzzy case, with of course significant differences.The concept of fuzzy sets as a continuum of grades of membership for the members of sets has been introduced by Zadeh (1965). Let N= {1, 2… n} be the set of all players. We will call uzzy coalition an n-dimensional vector 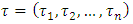 with
with 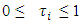 for each
for each 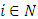 . A cooperative fuzzy game with the players set N is a pair
. A cooperative fuzzy game with the players set N is a pair 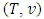 , where
, where 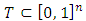 , is the set of fuzzy coalitions and
, is the set of fuzzy coalitions and 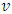 is the characteristic function of that game that maps a real number to each fuzzy coalition.The cooperative fuzzy games reflect type of situations in which for players allowed to take part in coalitions with participation levels that can vary from non-cooperation to full cooperation. Fuzzy coalitions reflect levels of participation at which players involved in cooperation. The reward for a player in this type of games defines depending on level of cooperation.An important topic of research for fuzzy cooperative theory is the extension of existing in classical theory decision concepts on fuzzy games. It is known, that not every classical concept has its natural counterpart for fuzzy games. At the same time some results in classical theory allow to be transformed on fuzzy case, with of course significant differences.Shapley value is the most studied concept in the classical cooperative theory. It’s generalization for the fuzzy games considered as one of the important topics for the fuzzy theory of games.There are known different approaches for extension of classical Shapley value on fuzzy cooperative games. Have been obtained different fuzzy values that depend on applied approaches. It pays to separate the Aubin’s (1981) diagonal value, which represents itself an integral formula for the Shapley value. For this and some other values it is specific, that they do not use all of the information that is in the square of fuzzy coalitions (in our case the latter one is an n-dimensional unit cube). The mentioned fact separates types of games to what the fuzzy Shapley value suitable. The value proposed by Tsurumi et al (2001) represents of itself a payoff vector for each fuzzy game that depends on the final formed coalition. Hwang and Liao (2009) gave a concept of value that results to a fuzzy Shapley value, where a payoff obtained for each level of participation. Jimenez-Losada et al. (2019) for the fuzzy cooperative games propose a new extension of the Shapley value that improves the known classical Shapley value for fuzzy cooperative games.Among the known axiomatizations for the fuzzy Shapley values can be separated Shapley (1953), Myerson (1980), Young (1985), Weber (1988), Hart and Mas-Colell ((1989), Casajus (2014). Each one of them demonstrates certain interesting properties of the Shapley value.This research in its entirety contains novel results. New is the offered approach on generalizing the classical Shapley value for the fuzzy coalition game. Among the aspects what are new in fuzzy theory should be separated the constructed functional, point of minimum for what is the fuzzy Shapley value. In classical cooperative games a payment for each player in coalition is a component of certain traditional payoff vector. In contrast to that for the discussed fuzzy model the payoff is a function
is the characteristic function of that game that maps a real number to each fuzzy coalition.The cooperative fuzzy games reflect type of situations in which for players allowed to take part in coalitions with participation levels that can vary from non-cooperation to full cooperation. Fuzzy coalitions reflect levels of participation at which players involved in cooperation. The reward for a player in this type of games defines depending on level of cooperation.An important topic of research for fuzzy cooperative theory is the extension of existing in classical theory decision concepts on fuzzy games. It is known, that not every classical concept has its natural counterpart for fuzzy games. At the same time some results in classical theory allow to be transformed on fuzzy case, with of course significant differences.Shapley value is the most studied concept in the classical cooperative theory. It’s generalization for the fuzzy games considered as one of the important topics for the fuzzy theory of games.There are known different approaches for extension of classical Shapley value on fuzzy cooperative games. Have been obtained different fuzzy values that depend on applied approaches. It pays to separate the Aubin’s (1981) diagonal value, which represents itself an integral formula for the Shapley value. For this and some other values it is specific, that they do not use all of the information that is in the square of fuzzy coalitions (in our case the latter one is an n-dimensional unit cube). The mentioned fact separates types of games to what the fuzzy Shapley value suitable. The value proposed by Tsurumi et al (2001) represents of itself a payoff vector for each fuzzy game that depends on the final formed coalition. Hwang and Liao (2009) gave a concept of value that results to a fuzzy Shapley value, where a payoff obtained for each level of participation. Jimenez-Losada et al. (2019) for the fuzzy cooperative games propose a new extension of the Shapley value that improves the known classical Shapley value for fuzzy cooperative games.Among the known axiomatizations for the fuzzy Shapley values can be separated Shapley (1953), Myerson (1980), Young (1985), Weber (1988), Hart and Mas-Colell ((1989), Casajus (2014). Each one of them demonstrates certain interesting properties of the Shapley value.This research in its entirety contains novel results. New is the offered approach on generalizing the classical Shapley value for the fuzzy coalition game. Among the aspects what are new in fuzzy theory should be separated the constructed functional, point of minimum for what is the fuzzy Shapley value. In classical cooperative games a payment for each player in coalition is a component of certain traditional payoff vector. In contrast to that for the discussed fuzzy model the payoff is a function 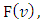 which satisfies to modified analogues of Shapley axioms. These axioms again have been newly formulated here. In different of values that obtained according to listed approaches, the Shapley value we propose defined for games on the unit cube that satisfy to the condition of integrability. That is much weaker condition than the requirement of being differentiable which is in case of Shapley’s some other fuzzy extensions. It makes essentially wider the class of fuzzy games to what the defined our way fuzzy Shapley value can be applied. For the fuzzy pre-value we research certain of known properties that hold true for classical Shapley value.Results included in paper devoted to generalizing of the classical Shapley value for fuzzy cooperative games, through one of the known approaches. According to that approach the classical Shapley value is the point of minimum for a certain functional on the set of all pre-imputations. Included in Section 2 preliminary facts and definitions that refer to cooperative games, the classical functional, fuzzy coalitions, and a simpler form for functional in case of fuzzy games, formulated fuzzy analogues of Shapley axioms. Has been defined the functional
which satisfies to modified analogues of Shapley axioms. These axioms again have been newly formulated here. In different of values that obtained according to listed approaches, the Shapley value we propose defined for games on the unit cube that satisfy to the condition of integrability. That is much weaker condition than the requirement of being differentiable which is in case of Shapley’s some other fuzzy extensions. It makes essentially wider the class of fuzzy games to what the defined our way fuzzy Shapley value can be applied. For the fuzzy pre-value we research certain of known properties that hold true for classical Shapley value.Results included in paper devoted to generalizing of the classical Shapley value for fuzzy cooperative games, through one of the known approaches. According to that approach the classical Shapley value is the point of minimum for a certain functional on the set of all pre-imputations. Included in Section 2 preliminary facts and definitions that refer to cooperative games, the classical functional, fuzzy coalitions, and a simpler form for functional in case of fuzzy games, formulated fuzzy analogues of Shapley axioms. Has been defined the functional 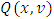 for the fuzzy case. Section 3 devoted to finding of a function
for the fuzzy case. Section 3 devoted to finding of a function 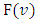 that minimizes
that minimizes  . For functions
. For functions  participating in the expression of functional
participating in the expression of functional 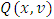 , formulated the requirements at what for the function
, formulated the requirements at what for the function 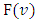 hold true the Shapley axioms. In section 4 has been discussed the properties of function
hold true the Shapley axioms. In section 4 has been discussed the properties of function 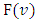 . It has been proven, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the pre-value
. It has been proven, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the pre-value 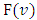 coincides with the classical Shapley pre-value.Further, has been obtained necessary and sufficient conditions at what the function
coincides with the classical Shapley pre-value.Further, has been obtained necessary and sufficient conditions at what the function 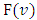 satisfies to the strengthened dummy’s axiom. Has been proven a preposition that allows constructing functions
satisfies to the strengthened dummy’s axiom. Has been proven a preposition that allows constructing functions 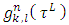 , which satisfy to the strengthen dummy’s axiom with fewer players.
, which satisfy to the strengthen dummy’s axiom with fewer players.
2. Preliminary Facts and Definitions
In SOBOLEV A. (1978) for classical cooperative games has been proved that the Shapley vector is a point of the set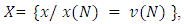 on what the functional
on what the functional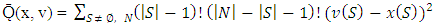 gets its minimum.That property of Shapley vector allows using it as an alternative definition. The defined that way Shapley vector in its turn by a quite natural way can be extended on fuzzy cooperative games.Let T be the set of all fuzzy coalitions, i.e.
gets its minimum.That property of Shapley vector allows using it as an alternative definition. The defined that way Shapley vector in its turn by a quite natural way can be extended on fuzzy cooperative games.Let T be the set of all fuzzy coalitions, i.e. 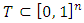 . A coalition in its classical sense is a peak of the cube T, or more precisely, that peak for what
. A coalition in its classical sense is a peak of the cube T, or more precisely, that peak for what For a measure
For a measure 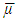 that concentrated on peaks
that concentrated on peaks 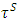 of the cube
of the cube 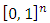 and accepts values
and accepts values 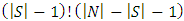 the expression for
the expression for 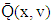 can be rewritten in a simpler form:
can be rewritten in a simpler form: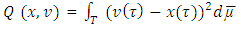 On the cube T instead of
On the cube T instead of 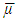 one can take an arbitrary measure and define the value
one can take an arbitrary measure and define the value 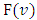 for a game
for a game 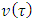 as a point on what the newly obtained functional
as a point on what the newly obtained functional 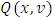 will reach its minimum.Farther we will choose a measure such that the function
will reach its minimum.Farther we will choose a measure such that the function 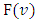 would possess with properties defined by axioms, similar to Shapley axioms for classical cooperative games.Below formulated analogs of Shapley axioms for fuzzy cooperative games.A1 (Symmetry) Let π is an injection from the set
would possess with properties defined by axioms, similar to Shapley axioms for classical cooperative games.Below formulated analogs of Shapley axioms for fuzzy cooperative games.A1 (Symmetry) Let π is an injection from the set 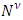 on
on 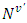 such, that for each coalition
such, that for each coalition 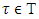
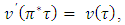 where
where 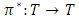 is a map, for what
is a map, for what 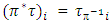 .Then, for all
.Then, for all 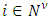
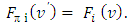 A.2 (Pareto optimality)
A.2 (Pareto optimality)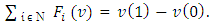 The unusual form of this axiom compared with its classical analogue caused by the fact that the possibility of
The unusual form of this axiom compared with its classical analogue caused by the fact that the possibility of 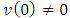 not excluded.A.3 (Inefficiency of ‘dummy’) If in the game
not excluded.A.3 (Inefficiency of ‘dummy’) If in the game 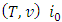 is a player such, that
is a player such, that 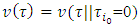 , for arbitrary
, for arbitrary 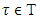 , then
, then 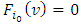 . The expression
. The expression 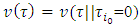 means, that the value of the coalition
means, that the value of the coalition 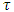 in the game
in the game 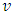 equals to the same value for the coalition with
equals to the same value for the coalition with 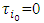 .A.4 (Aggregation) If
.A.4 (Aggregation) If 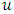 and
and 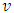 are games with the same set of coalitions T and
are games with the same set of coalitions T and 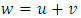 , then
, then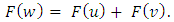 Besides A.3 we will also deal with its strengthened form. There will be a need for the next definition.Definition 1. We will say that the game
Besides A.3 we will also deal with its strengthened form. There will be a need for the next definition.Definition 1. We will say that the game 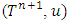 derived from the game
derived from the game 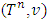 by adding to it a ‘dummy’ player
by adding to it a ‘dummy’ player 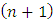 , if for every coalition
, if for every coalition 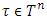 and every
and every 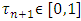 takes place:
takes place: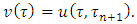 A3’. (The strengthened axiom of ‘dummy’) Holds true
A3’. (The strengthened axiom of ‘dummy’) Holds true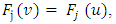 for arbitrary
for arbitrary 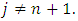 The A3’ otherwise, means that including a ‘dummy’ in a game does not change gains of other players.It is obvious, that if A.2 remains true, then the A.3 follows from A.3’.In general the choice of measure µ is not unique. Partially as such a measure can be also
The A3’ otherwise, means that including a ‘dummy’ in a game does not change gains of other players.It is obvious, that if A.2 remains true, then the A.3 follows from A.3’.In general the choice of measure µ is not unique. Partially as such a measure can be also 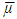 . The axiom A.1 holds true, if the measure has been defined the same way on all of the sides of the cube.Let now consider the following sets. For arbitrary
. The axiom A.1 holds true, if the measure has been defined the same way on all of the sides of the cube.Let now consider the following sets. For arbitrary 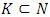 and
and 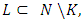 denote by
denote by 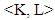 the following set:
the following set: 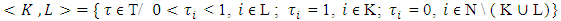
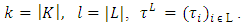 Sets <K, L> actually are the faces of the cube
Sets <K, L> actually are the faces of the cube 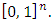 We will deal with the case, when on each one of its faces measure defined by a density function
We will deal with the case, when on each one of its faces measure defined by a density function 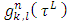 . To satisfy axiom A.1 will be accepted that
. To satisfy axiom A.1 will be accepted that 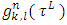 are symmetric, none negative functions of their arguments. As a result, we will have the following functional:
are symmetric, none negative functions of their arguments. As a result, we will have the following functional: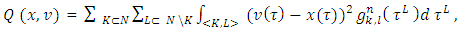 where
where 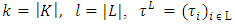 .Our goal is finding relations between the functions
.Our goal is finding relations between the functions 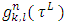 so that the function
so that the function 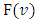 which minimizes functional
which minimizes functional 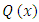 , has satisfied to axioms A.3 and A.3’.
, has satisfied to axioms A.3 and A.3’.
3. Pre-value for Fuzzy Cooperative Games
Below we will find explicit formula for the function 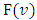 , which minimizes functional
, which minimizes functional 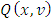 . At the same time for functions
. At the same time for functions 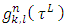 participating in the expression of functional
participating in the expression of functional 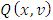 , we will formulate requirements so that with them hold true the Shapley axioms for
, we will formulate requirements so that with them hold true the Shapley axioms for 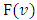 .Farther we will use the defined below magnitudes:
.Farther we will use the defined below magnitudes: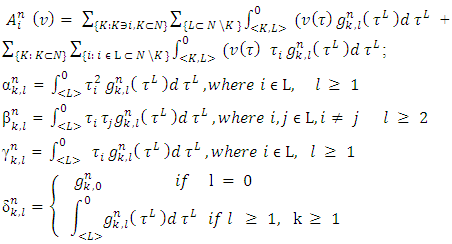 Let extend definitions of
Let extend definitions of 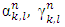 for
for  and
and 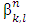 for
for 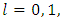 by accepting that
by accepting that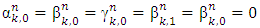 . Besides, let also accept that
. Besides, let also accept that 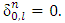 Further we will need to deal with numbers:
Further we will need to deal with numbers: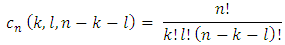 We denote:
We denote: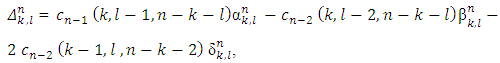 and
and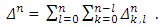 Preposition 1. If
Preposition 1. If 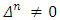 , then the functional Q(x, v) on the set
, then the functional Q(x, v) on the set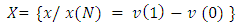 its minimum by x accepts on the vector
its minimum by x accepts on the vector 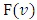 with following components:
with following components: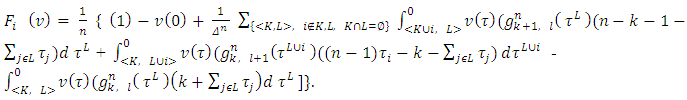 | (1) |
Proof. The vector on what functional 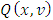 reaches its minimum, according to the method of Lagrange’s multipliers should satisfy to the following system of linear equations:
reaches its minimum, according to the method of Lagrange’s multipliers should satisfy to the following system of linear equations: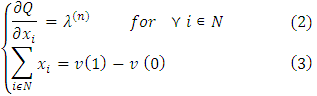 To write these equations in explicit form we need to find the partial differentials of
To write these equations in explicit form we need to find the partial differentials of 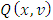 :
: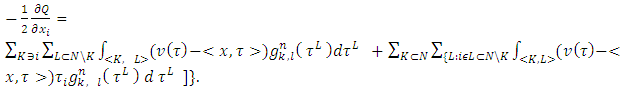 There will be need as well for the following notations:
There will be need as well for the following notations: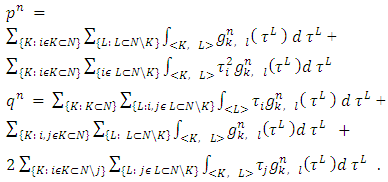 We need to prove that
We need to prove that 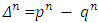 . So, let rewrite the expressions for
. So, let rewrite the expressions for 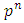 and
and 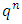 in different forms:
in different forms: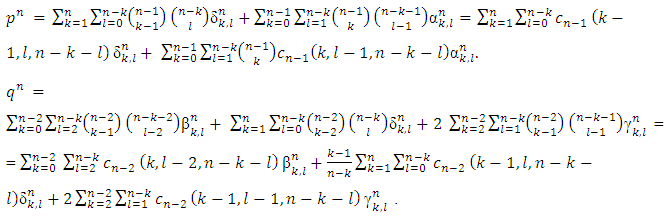 As far as above we redefined the magnitudes
As far as above we redefined the magnitudes 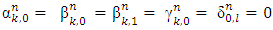 , so, while figuring out the difference
, so, while figuring out the difference 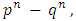 we can formally extend summing by the index k from 0 to n and by the index l from 0 to
we can formally extend summing by the index k from 0 to n and by the index l from 0 to 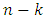 . That will result the required equality instantly.Further, by using the defined above notations we can rewrite (2) - (3) in an equivalent form:
. That will result the required equality instantly.Further, by using the defined above notations we can rewrite (2) - (3) in an equivalent form: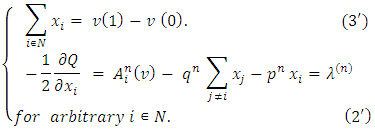 Summing equations (2’) by i and taking in account the (3’), we will obtain, that
Summing equations (2’) by i and taking in account the (3’), we will obtain, that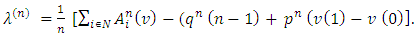 That expression for
That expression for 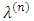 together with the system (2’) – (3’) gives:
together with the system (2’) – (3’) gives: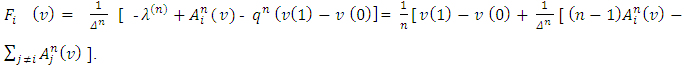 Submitting in this formula the expression for
Submitting in this formula the expression for 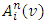 and uniting the integrals with coinciding domains of integration, we will have the following expression for
and uniting the integrals with coinciding domains of integration, we will have the following expression for 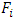
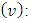
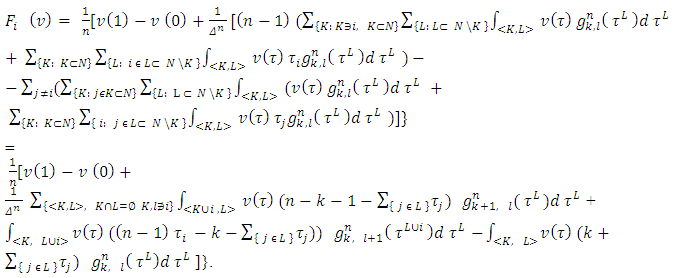 As a result we have obtained the required formula (2.1).Remark.1. In general the solution
As a result we have obtained the required formula (2.1).Remark.1. In general the solution 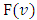 for system (2) - (3) is unique for arbitrary (and not only for not negative) functions
for system (2) - (3) is unique for arbitrary (and not only for not negative) functions 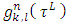 , which participate in
, which participate in 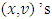 expression. The obtained that way solution for system (2) - (3) still can be accepted as some analogue for the Shapley function, despite of that it already may not minimize the functional
expression. The obtained that way solution for system (2) - (3) still can be accepted as some analogue for the Shapley function, despite of that it already may not minimize the functional 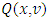 .Remark.2. For a functional
.Remark.2. For a functional 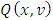 with arbitrary measure μ the
with arbitrary measure μ the 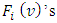 expression becomes much simpler. So let
expression becomes much simpler. So let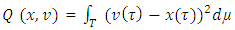 By using the following notations,
By using the following notations,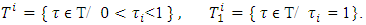 We can rewrite the expression for
We can rewrite the expression for 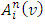 the following way:
the following way: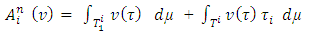 By submitting that expression for
By submitting that expression for 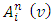 in the formula for
in the formula for 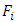
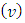 , we will have that
, we will have that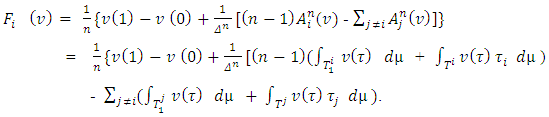 | (4) |
Proposition 2. Let 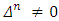 . For the function
. For the function 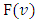 to satisfy axiom A3 it is necessary and sufficient, that hold true the following equations:
to satisfy axiom A3 it is necessary and sufficient, that hold true the following equations: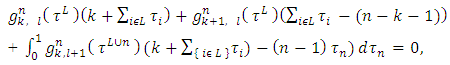 | (5) |
For such pairs 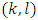 that
that 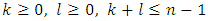 , besides
, besides 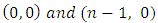 . In addition will also take place the following equations:
. In addition will also take place the following equations: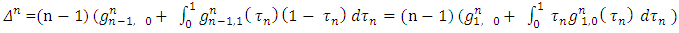 | (6) |
Proof. We will derive the conditions (5) based on axiom A3. That way we will prove the necessity of our statement. While doing so, due to the reversibility of applied judgments we will also prove the sufficiency of this proposition.We will accept, that the player n is a ‘dummy’, i.e. 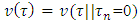 , for all
, for all 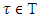 .The integral equations below take place due to the ‘dummies’ property:
.The integral equations below take place due to the ‘dummies’ property: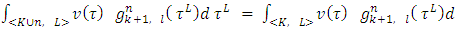 | (7) |
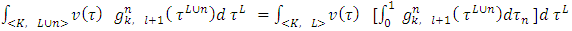 | (8) |
From formula (1) for the component 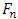
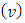 by using equalities (7) and (8), we will obtain the following expression:
by using equalities (7) and (8), we will obtain the following expression: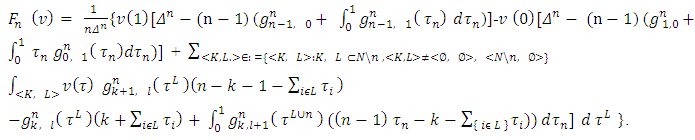
 based on the axiom A3. At the same time
based on the axiom A3. At the same time 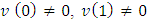 and
and 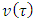 is for arbitrary coalition
is for arbitrary coalition 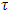 . From there, the expressions in square brackets should be equal to 0. Hence, as a result we will obtain the equations (5) and (6).To conclude it is remaining to show, that the equations (6) can be derived from (5), to what will be devoted the rest of the proof.Let consider the following magnitudes:
. From there, the expressions in square brackets should be equal to 0. Hence, as a result we will obtain the equations (5) and (6).To conclude it is remaining to show, that the equations (6) can be derived from (5), to what will be devoted the rest of the proof.Let consider the following magnitudes: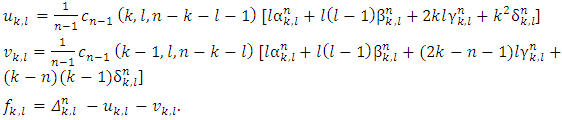 | (9) |
That statement we will prove trough the next four lemmas.Lemma 1. Takes place the following equation: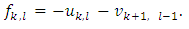 | (10) |
Proof. Let 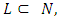 and
and 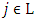 . We will consider the integral below:
. We will consider the integral below: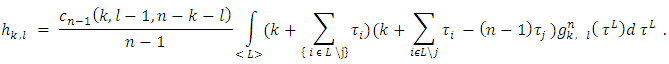 Let transform the sub integral expression by using the symmetry of functions
Let transform the sub integral expression by using the symmetry of functions 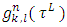 and invented in the beginning notations:
and invented in the beginning notations: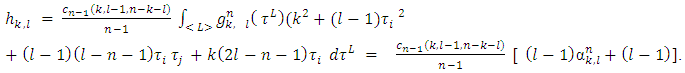 The expression below we will obtain by applying the condition (5) to the integral
The expression below we will obtain by applying the condition (5) to the integral 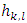 :
: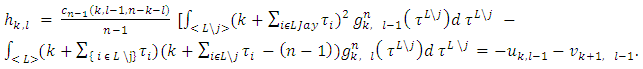 That is what has been required to prove.Lemma 2. For every
That is what has been required to prove.Lemma 2. For every 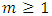 , takes place the following presentation:
, takes place the following presentation: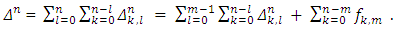 | (12) |
Proof. This statement we will prove by using the method of mathematical induction.1. Let prove first, that the statement is correct for 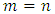 . Really, as far as
. Really, as far as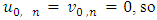
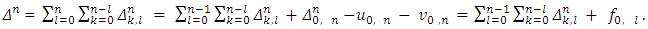 2. Accept that the expression (12) is correct for arbitrary m. We will use the formula (11) of the Lemma 1, as well as the equalities:
2. Accept that the expression (12) is correct for arbitrary m. We will use the formula (11) of the Lemma 1, as well as the equalities: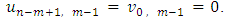 Below we have performed some quite natural transformations:
Below we have performed some quite natural transformations: 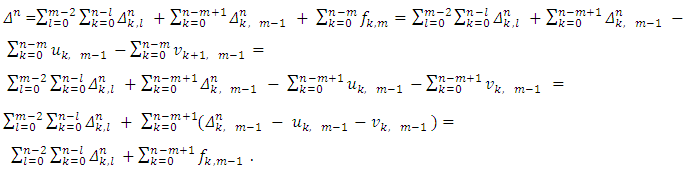 The lemma has been proved.
The lemma has been proved.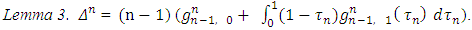 Proof. For
Proof. For 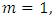 according to presentation from the Lemma 2,
according to presentation from the Lemma 2,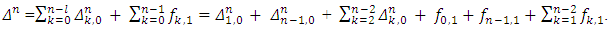 Based on formulas (11) and (10),
Based on formulas (11) and (10),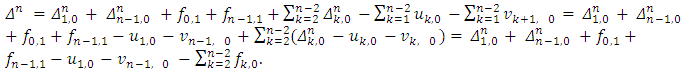 Let submit in the obtained expression submit values for the following magnitudes:
Let submit in the obtained expression submit values for the following magnitudes: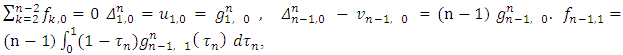 We will have the final expression
We will have the final expression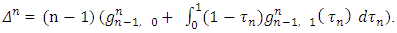
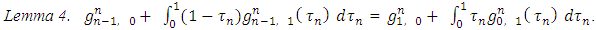 Proof. Below we are integrating the equality (5) by the domain
Proof. Below we are integrating the equality (5) by the domain 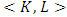 and using the notations above:
and using the notations above: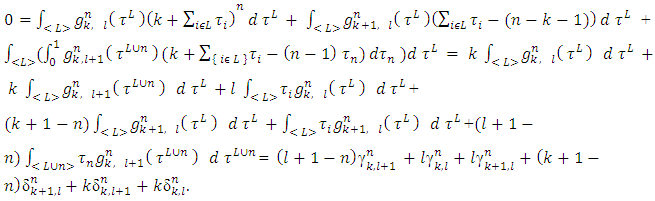 If to multiply the equalities above by
If to multiply the equalities above by 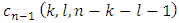 and sum them by all pairs
and sum them by all pairs 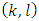 ,for what takes place the (5), then we will obtain:
,for what takes place the (5), then we will obtain: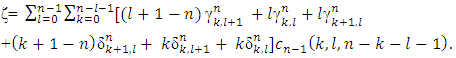 As far as
As far as 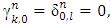 so we will have, that
so we will have, that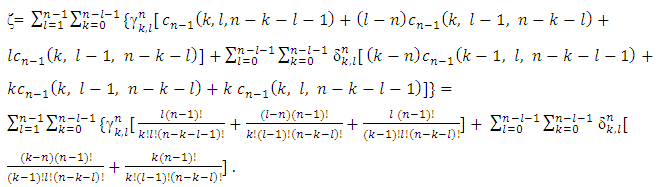 Expressions in the square brackets are equal to each other:
Expressions in the square brackets are equal to each other: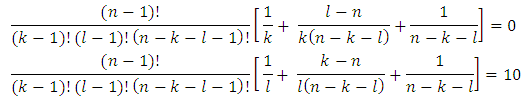 As a result
As a result 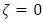 .Now recall that (5) takes place for pairs
.Now recall that (5) takes place for pairs 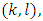 where that
where that 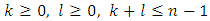 , besides the pairs
, besides the pairs 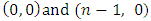 .If in the written above expression to separate from the sum members that correspond to pairs
.If in the written above expression to separate from the sum members that correspond to pairs 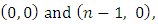 then based on (5) the remaining will be equal to 0.The separated members will give us the following expression:
then based on (5) the remaining will be equal to 0.The separated members will give us the following expression: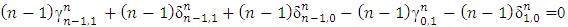 By substituting the values for participating magnitudes, we will obtain what has been required:
By substituting the values for participating magnitudes, we will obtain what has been required: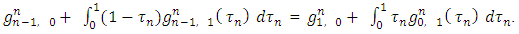 The last two lemmas conclude the proof of preposition 2.
The last two lemmas conclude the proof of preposition 2.
4. Properties of the Function F(ν)
Let 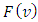 be the pre-value for the game
be the pre-value for the game 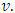 That means, it is the point on what the functional
That means, it is the point on what the functional 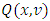 reaches its minimum, and participating in
reaches its minimum, and participating in 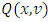 functions
functions 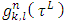 satisfy to the specified for
satisfy to the specified for 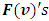 Shapley axioms conditions.In this paragraph we will show, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the prevalue
Shapley axioms conditions.In this paragraph we will show, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the prevalue 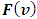 coincides with the Shapley prevalue for the classical game. Further, we will obtain necessary and sufficient conditions at what the function
coincides with the Shapley prevalue for the classical game. Further, we will obtain necessary and sufficient conditions at what the function 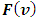 satisfies to the strengthened dummies axiom. We will also prove a preposition allowing constructing functions
satisfies to the strengthened dummies axiom. We will also prove a preposition allowing constructing functions 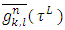 that satisfy to the axiom
that satisfy to the axiom 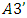 for fewer players.4.1. Fuzzy games we are going to deal with defined through certain n dimensional distribution functions
for fewer players.4.1. Fuzzy games we are going to deal with defined through certain n dimensional distribution functions 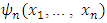 , that are continuous by each one of their arguments and satisfy to following condition:
, that are continuous by each one of their arguments and satisfy to following condition: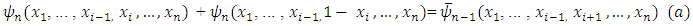 where
where 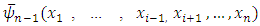 is some
is some 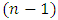 dimensional distribution function of variables
dimensional distribution function of variables 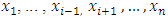 and possesses with the same kind of properties as functions
and possesses with the same kind of properties as functions 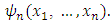 Preposition 3. Let
Preposition 3. Let 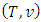 is a fuzzy game that obtained from a classical game
is a fuzzy game that obtained from a classical game 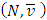 by the following way:
by the following way: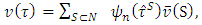 | (13) |
where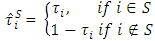 and
and 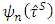 is a function that satisfies to the condition
is a function that satisfies to the condition 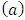 . If
. If 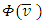 is the Shapley prevalue for game
is the Shapley prevalue for game 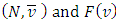 the prevalue for fuzzy game
the prevalue for fuzzy game 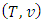 then
then 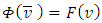 .Proof. Let
.Proof. Let 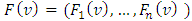 is the solution for system
is the solution for system 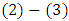 of game
of game 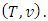 By using the explicit expression (4) for
By using the explicit expression (4) for 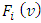 and formula (13) we can prove that
and formula (13) we can prove that 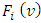 allows some linear representation that depends on
allows some linear representation that depends on 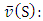
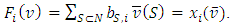
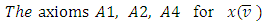 hold true due to properties of
hold true due to properties of 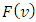 . So to prove our statement, we need to show, that for
. So to prove our statement, we need to show, that for 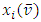 (takes place the ‘dummies’ axiom. So, we need to prove that if a player
(takes place the ‘dummies’ axiom. So, we need to prove that if a player 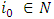 is a dummy in the game
is a dummy in the game 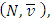 then
then 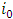 is so also in
is so also in 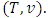 Let for all
Let for all 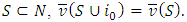 Then
Then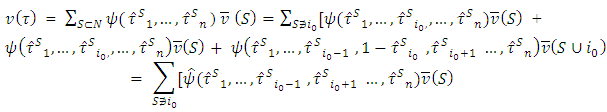 By the other side:
By the other side: 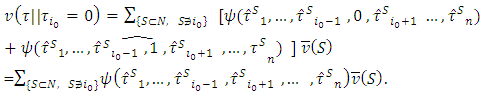 From there
From there 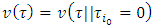 , and hence,
, and hence, 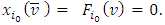 As a result we have obtained that the prevalue
As a result we have obtained that the prevalue 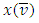 satisfies to all of the Shapley axioms, which means, that
satisfies to all of the Shapley axioms, which means, that 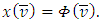 Remark. In a special case, when players participate in coalition independently of each other, i.e., when
Remark. In a special case, when players participate in coalition independently of each other, i.e., when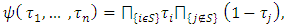 then
then 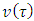 is a multilinear extension of Owen. One can check it easily, that then for functions
is a multilinear extension of Owen. One can check it easily, that then for functions 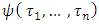 takes place the condition
takes place the condition 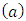 .Below we will derive relations that concern to the strengthened axiom of ‘dummy’.Preposition 4. Let
.Below we will derive relations that concern to the strengthened axiom of ‘dummy’.Preposition 4. Let 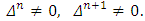 The function
The function 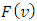 in an
in an 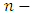 person game satisfies to the strengthened ‘dummies’ axiom if and only if, when for all such pairs
person game satisfies to the strengthened ‘dummies’ axiom if and only if, when for all such pairs 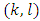 that
that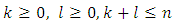 , besides the
, besides the 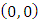 and
and 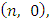 takes place the following equation:
takes place the following equation: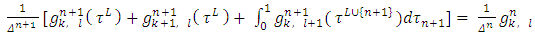 | (14) |
and the equation (5) for the 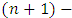 players game:
players game: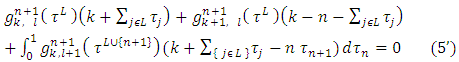 Proof. Necessity. The equation
Proof. Necessity. The equation 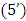 follows from the Proposition2, because, if the axiom A2. holds true, then A3 follows from the A3’.The same way, as we did it in case of formula (2.1), let again write the expression for
follows from the Proposition2, because, if the axiom A2. holds true, then A3 follows from the A3’.The same way, as we did it in case of formula (2.1), let again write the expression for 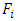
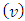 by separating the player
by separating the player 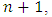 while summing by the side
while summing by the side 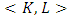 of the cube and replacing
of the cube and replacing 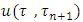 by
by 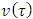 , based on the equation
, based on the equation 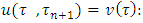
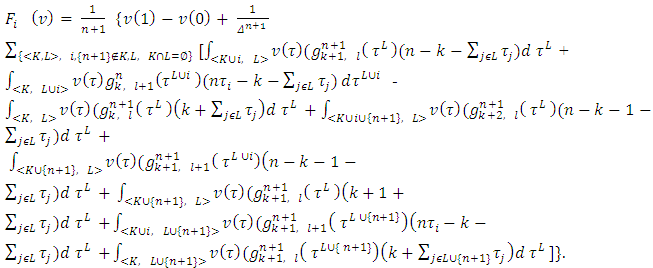 | (15) |
The formula (1) also gives as an expression for 
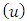 . According to the strengthened axiom of ‘dummy’, gains for the same player
. According to the strengthened axiom of ‘dummy’, gains for the same player 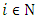 in both of the games
in both of the games 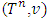 and
and 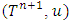 are the same. That is the reason because of what the obtained for
are the same. That is the reason because of what the obtained for 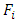
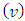 and
and 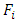
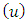 expressions are equal. Let write that equation:
expressions are equal. Let write that equation: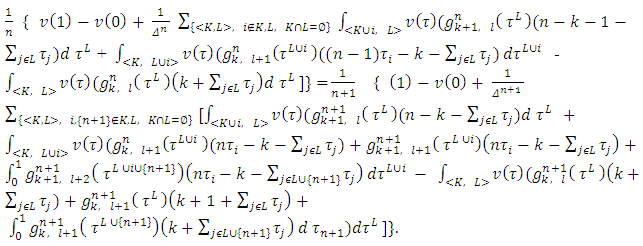 By equalizing coefficients at
By equalizing coefficients at 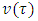 for similar coalitions in both of the sides of equation we will obtain relations that connect functions
for similar coalitions in both of the sides of equation we will obtain relations that connect functions 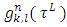 and
and 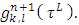 Forms of the mentioned coefficients depend on the cubes sides to what coalition
Forms of the mentioned coefficients depend on the cubes sides to what coalition 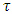 belongs. More precisely, to which one of the sets
belongs. More precisely, to which one of the sets 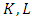 or
or 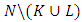 belongs the player i. Besides that special views have the coefficients at
belongs the player i. Besides that special views have the coefficients at 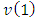 and
and 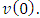 As a result we will have, that the equality
As a result we will have, that the equality 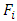
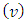 =
= 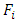
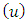 (i.e. the axiom A3’) is equivalent to the following five relations.The equality of coefficients at
(i.e. the axiom A3’) is equivalent to the following five relations.The equality of coefficients at 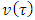 for
for 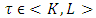 , where
, where 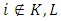 (besides the side
(besides the side 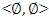 ) gives as the relation:
) gives as the relation: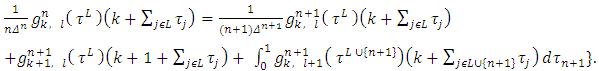 | (16) |
for all pairs 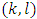 that
that 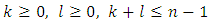 , besides the pair
, besides the pair 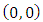 .For the sides
.For the sides 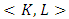 , where
, where 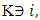 besides the side
besides the side 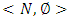 , we will obtain the following relation:
, we will obtain the following relation: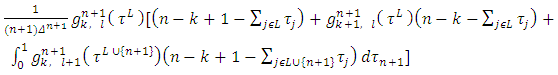 | (17) |
which takes place for all pairs 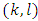 that
that 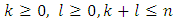 , besides the pair
, besides the pair 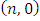 .For the sides
.For the sides 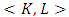 , where
, where 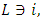 we will obtain the following relation:
we will obtain the following relation: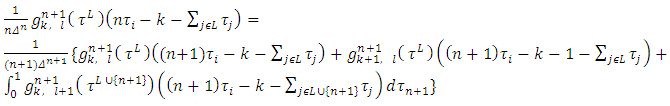 | (18) |
which is correct for all pairs 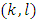 that
that 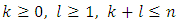 .Finally, by equalizing the coefficients at
.Finally, by equalizing the coefficients at 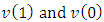 we will obtain
we will obtain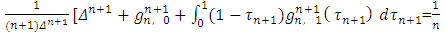 | (19) |
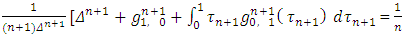 | (20) |
Adding to each other the equalities (16) and (17) we will obtain that (14) takes place for pairs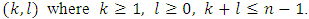 Adding to each other equalities (16) and (18) and dividing the sum by
Adding to each other equalities (16) and (18) and dividing the sum by 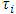 we will obtain that (14) takes place for pairs
we will obtain that (14) takes place for pairs 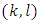 where
where 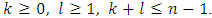 Subtracting from each other the equalities (16) and (18) and dividing the result by
Subtracting from each other the equalities (16) and (18) and dividing the result by 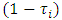 we will have that (14) takes place for pairs
we will have that (14) takes place for pairs 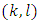 , where
, where 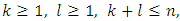 besides the pair
besides the pair 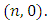 So, we have proved that the equality (14) takes place for all pairs
So, we have proved that the equality (14) takes place for all pairs 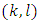 that
that 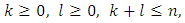 besides the pairs
besides the pairs 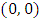 and
and 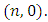 The Proposition takes place for pairs
The Proposition takes place for pairs 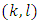 , where has been proved fully.Below proved one more proposition that allows constructing functions
, where has been proved fully.Below proved one more proposition that allows constructing functions 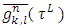 such that for
such that for 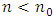 satisfy equations (5) if they do the same for
satisfy equations (5) if they do the same for 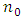 .Proposition 5. Let for some
.Proposition 5. Let for some 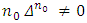 and for functions
and for functions 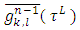 ,
,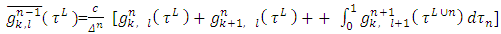 | (21) |
take place equations (5). Then 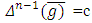 and functions
and functions 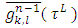 satisfy to the equation (5) too.Proof. The equation
satisfy to the equation (5) too.Proof. The equation 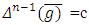 can be proved by using equations (21) and the known earlier formula, but this time for
can be proved by using equations (21) and the known earlier formula, but this time for 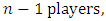 i.e.
i.e.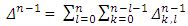 To check that functions
To check that functions 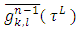 satisfy (5) it is enough using the formula (21) to figure out taking part in (5) magnitudes that written for (n−1), and after that summing them by taking in account that the (5) takes place for the n −game.3. Below are examples for the sets of none negative functions that satisfy to ‘dummies’ axiom in case of some fixed number of players n.Example 1. Simplest is the set of functions
satisfy (5) it is enough using the formula (21) to figure out taking part in (5) magnitudes that written for (n−1), and after that summing them by taking in account that the (5) takes place for the n −game.3. Below are examples for the sets of none negative functions that satisfy to ‘dummies’ axiom in case of some fixed number of players n.Example 1. Simplest is the set of functions 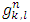 defined the following way:
defined the following way: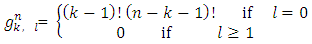 Gain of a player in case of defined functions depends only on game’s value on the peaks of cube
Gain of a player in case of defined functions depends only on game’s value on the peaks of cube 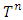 , which are the coalitions in the classical sense. The functional
, which are the coalitions in the classical sense. The functional 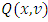 in its turn coincides with the functional
in its turn coincides with the functional 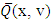 that defined for classical cooperative games.Example 2. Let for some n define functions
that defined for classical cooperative games.Example 2. Let for some n define functions 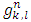 the following way:
the following way: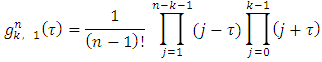
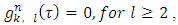 and by using the formula below recurrently define
and by using the formula below recurrently define 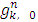 :
: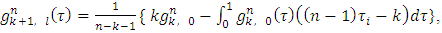 where one can choose
where one can choose 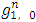 arbitrary, but big enough to get
arbitrary, but big enough to get 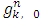 none negative.For l=0 equations (5) immediately follow from the formula that recurrently defines theFunctions
none negative.For l=0 equations (5) immediately follow from the formula that recurrently defines theFunctions 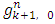 .For l=1 we have:
.For l=1 we have: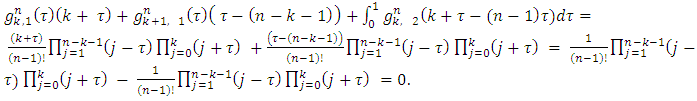 Further we will apply the Proposition 5, by accepting that
Further we will apply the Proposition 5, by accepting that 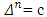 . Let check, that for
. Let check, that for 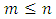 the functions
the functions 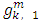 can be defined by the formula (21):
can be defined by the formula (21):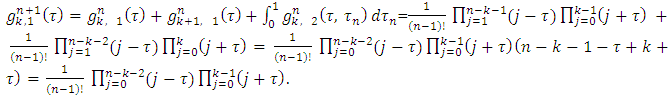 That way we have constructed example of functions
That way we have constructed example of functions 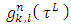 that satisfy to the axiom
that satisfy to the axiom 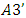 for some number of players n that does not succeed to certain
for some number of players n that does not succeed to certain  However, doing the same for arbitrary n this method unfortunately does not allow.We should mention, that in this example essential are only those coalitions, which get described by peaks and the line segments that connect adjacent peaks of cube
However, doing the same for arbitrary n this method unfortunately does not allow.We should mention, that in this example essential are only those coalitions, which get described by peaks and the line segments that connect adjacent peaks of cube 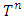 .Example 3. For
.Example 3. For 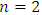 to axiom A3 satisfy the following functions that defined on square:
to axiom A3 satisfy the following functions that defined on square: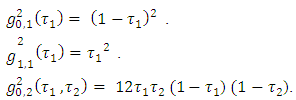 Remark 4. All of the functions
Remark 4. All of the functions 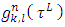 that constructed in examples above satisfy to the following condition:
that constructed in examples above satisfy to the following condition: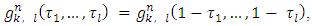 which can be considered as another property for the distribution functions
which can be considered as another property for the distribution functions 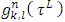 .As a conclusion the author would like to appreciate any information about copyright breach of these results.
.As a conclusion the author would like to appreciate any information about copyright breach of these results.
ACKNOWLEDGEMENTS
The author thanks the editor and two anonymous referees for their helpful suggestions.
References
| [1] | AUBIN JP (1981). Cooperative fuzzy games. Math Oper.res 6: 1-13. |
| [2] | CASAJUS A. (2013). The Shapley value without efficiency and additivity. Mathematical Social Sciences 68(1): 1-4. |
| [3] | HART S. and MAS-COLELL A. (1989). Potential, value and consistency. Econometrica 57(3): 589-614. |
| [4] | HWANG Y.A. and LIAO Y.H. (2009). The consistent value of fuzzy games. Fuzzy Sets and Systems 160: 644-656. |
| [5] | JIMENENEZ-LOSADA A. et al. (2019). A new Shapley value for games with fuzzy coalitions. Fuzzy Sets and Systems. January 20019. |
| [6] | MYERSON R.B. (1980). Conferences structures and fair allocation rules. International Journal of Game Theory 9: 169-182. |
| [7] | SHAPLEY L.S. (1953). A value for n-person games, in: The Shapley Value, A.W. Tucker and H. Kuhn (Eds.), Annals of Mathematics Studies, Vol. 28. Princeton University Press: 307-317. |
| [8] | SOBOLEV A. (1978). Nonlinear analogues of Shapley function. – Modern Directions in Game Theory - Vilnius, pp.119-126. (In Russian). |
| [9] | TSURUMI M., TANINO T. and INUIGUCHI, M. (2001). A Shapley function on a class of cooperative fuzzy games. European Journal of Operational Research 129: 596-618. |
| [10] | WEBER R.J. (1988). Probabilistic values for games. In: The Shapley Value. Roth A.R. (eds). Cambridge University Press. |
| [11] | YOUNG H.P. (1985). Monotonic solutions of cooperative games. International Journal of Game Theory 14: 65-72. |
| [12] | ZADEH L. A. (1965). Fuzzy sets. Information Control 8: 338-353. |


 with
with 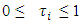 for each
for each 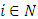 . A cooperative fuzzy game with the players set N is a pair
. A cooperative fuzzy game with the players set N is a pair 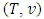 , where
, where 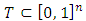 , is the set of fuzzy coalitions and
, is the set of fuzzy coalitions and 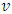 is the characteristic function of that game that maps a real number to each fuzzy coalition.The cooperative fuzzy games reflect type of situations in which for players allowed to take part in coalitions with participation levels that can vary from non-cooperation to full cooperation. Fuzzy coalitions reflect levels of participation at which players involved in cooperation. The reward for a player in this type of games defines depending on level of cooperation.An important topic of research for fuzzy cooperative theory is the extension of existing in classical theory decision concepts on fuzzy games. It is known, that not every classical concept has its natural counterpart for fuzzy games. At the same time some results in classical theory allow to be transformed on fuzzy case, with of course significant differences.Shapley value is the most studied concept in the classical cooperative theory. It’s generalization for the fuzzy games considered as one of the important topics for the fuzzy theory of games.There are known different approaches for extension of classical Shapley value on fuzzy cooperative games. Have been obtained different fuzzy values that depend on applied approaches. It pays to separate the Aubin’s (1981) diagonal value, which represents itself an integral formula for the Shapley value. For this and some other values it is specific, that they do not use all of the information that is in the square of fuzzy coalitions (in our case the latter one is an n-dimensional unit cube). The mentioned fact separates types of games to what the fuzzy Shapley value suitable. The value proposed by Tsurumi et al (2001) represents of itself a payoff vector for each fuzzy game that depends on the final formed coalition. Hwang and Liao (2009) gave a concept of value that results to a fuzzy Shapley value, where a payoff obtained for each level of participation. Jimenez-Losada et al. (2019) for the fuzzy cooperative games propose a new extension of the Shapley value that improves the known classical Shapley value for fuzzy cooperative games.Among the known axiomatizations for the fuzzy Shapley values can be separated Shapley (1953), Myerson (1980), Young (1985), Weber (1988), Hart and Mas-Colell ((1989), Casajus (2014). Each one of them demonstrates certain interesting properties of the Shapley value.This research in its entirety contains novel results. New is the offered approach on generalizing the classical Shapley value for the fuzzy coalition game. Among the aspects what are new in fuzzy theory should be separated the constructed functional, point of minimum for what is the fuzzy Shapley value. In classical cooperative games a payment for each player in coalition is a component of certain traditional payoff vector. In contrast to that for the discussed fuzzy model the payoff is a function
is the characteristic function of that game that maps a real number to each fuzzy coalition.The cooperative fuzzy games reflect type of situations in which for players allowed to take part in coalitions with participation levels that can vary from non-cooperation to full cooperation. Fuzzy coalitions reflect levels of participation at which players involved in cooperation. The reward for a player in this type of games defines depending on level of cooperation.An important topic of research for fuzzy cooperative theory is the extension of existing in classical theory decision concepts on fuzzy games. It is known, that not every classical concept has its natural counterpart for fuzzy games. At the same time some results in classical theory allow to be transformed on fuzzy case, with of course significant differences.Shapley value is the most studied concept in the classical cooperative theory. It’s generalization for the fuzzy games considered as one of the important topics for the fuzzy theory of games.There are known different approaches for extension of classical Shapley value on fuzzy cooperative games. Have been obtained different fuzzy values that depend on applied approaches. It pays to separate the Aubin’s (1981) diagonal value, which represents itself an integral formula for the Shapley value. For this and some other values it is specific, that they do not use all of the information that is in the square of fuzzy coalitions (in our case the latter one is an n-dimensional unit cube). The mentioned fact separates types of games to what the fuzzy Shapley value suitable. The value proposed by Tsurumi et al (2001) represents of itself a payoff vector for each fuzzy game that depends on the final formed coalition. Hwang and Liao (2009) gave a concept of value that results to a fuzzy Shapley value, where a payoff obtained for each level of participation. Jimenez-Losada et al. (2019) for the fuzzy cooperative games propose a new extension of the Shapley value that improves the known classical Shapley value for fuzzy cooperative games.Among the known axiomatizations for the fuzzy Shapley values can be separated Shapley (1953), Myerson (1980), Young (1985), Weber (1988), Hart and Mas-Colell ((1989), Casajus (2014). Each one of them demonstrates certain interesting properties of the Shapley value.This research in its entirety contains novel results. New is the offered approach on generalizing the classical Shapley value for the fuzzy coalition game. Among the aspects what are new in fuzzy theory should be separated the constructed functional, point of minimum for what is the fuzzy Shapley value. In classical cooperative games a payment for each player in coalition is a component of certain traditional payoff vector. In contrast to that for the discussed fuzzy model the payoff is a function 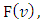 which satisfies to modified analogues of Shapley axioms. These axioms again have been newly formulated here. In different of values that obtained according to listed approaches, the Shapley value we propose defined for games on the unit cube that satisfy to the condition of integrability. That is much weaker condition than the requirement of being differentiable which is in case of Shapley’s some other fuzzy extensions. It makes essentially wider the class of fuzzy games to what the defined our way fuzzy Shapley value can be applied. For the fuzzy pre-value we research certain of known properties that hold true for classical Shapley value.Results included in paper devoted to generalizing of the classical Shapley value for fuzzy cooperative games, through one of the known approaches. According to that approach the classical Shapley value is the point of minimum for a certain functional on the set of all pre-imputations. Included in Section 2 preliminary facts and definitions that refer to cooperative games, the classical functional, fuzzy coalitions, and a simpler form for functional in case of fuzzy games, formulated fuzzy analogues of Shapley axioms. Has been defined the functional
which satisfies to modified analogues of Shapley axioms. These axioms again have been newly formulated here. In different of values that obtained according to listed approaches, the Shapley value we propose defined for games on the unit cube that satisfy to the condition of integrability. That is much weaker condition than the requirement of being differentiable which is in case of Shapley’s some other fuzzy extensions. It makes essentially wider the class of fuzzy games to what the defined our way fuzzy Shapley value can be applied. For the fuzzy pre-value we research certain of known properties that hold true for classical Shapley value.Results included in paper devoted to generalizing of the classical Shapley value for fuzzy cooperative games, through one of the known approaches. According to that approach the classical Shapley value is the point of minimum for a certain functional on the set of all pre-imputations. Included in Section 2 preliminary facts and definitions that refer to cooperative games, the classical functional, fuzzy coalitions, and a simpler form for functional in case of fuzzy games, formulated fuzzy analogues of Shapley axioms. Has been defined the functional 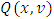 for the fuzzy case. Section 3 devoted to finding of a function
for the fuzzy case. Section 3 devoted to finding of a function 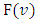 that minimizes
that minimizes 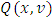 . For functions
. For functions 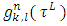 participating in the expression of functional
participating in the expression of functional 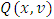 , formulated the requirements at what for the function
, formulated the requirements at what for the function 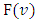 hold true the Shapley axioms. In section 4 has been discussed the properties of function
hold true the Shapley axioms. In section 4 has been discussed the properties of function 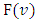 . It has been proven, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the pre-value
. It has been proven, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the pre-value 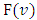 coincides with the classical Shapley pre-value.Further, has been obtained necessary and sufficient conditions at what the function
coincides with the classical Shapley pre-value.Further, has been obtained necessary and sufficient conditions at what the function 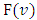 satisfies to the strengthened dummy’s axiom. Has been proven a preposition that allows constructing functions
satisfies to the strengthened dummy’s axiom. Has been proven a preposition that allows constructing functions 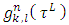 , which satisfy to the strengthen dummy’s axiom with fewer players.
, which satisfy to the strengthen dummy’s axiom with fewer players.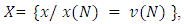 on what the functional
on what the functional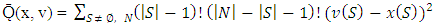 gets its minimum.That property of Shapley vector allows using it as an alternative definition. The defined that way Shapley vector in its turn by a quite natural way can be extended on fuzzy cooperative games.Let T be the set of all fuzzy coalitions, i.e.
gets its minimum.That property of Shapley vector allows using it as an alternative definition. The defined that way Shapley vector in its turn by a quite natural way can be extended on fuzzy cooperative games.Let T be the set of all fuzzy coalitions, i.e. 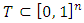 . A coalition in its classical sense is a peak of the cube T, or more precisely, that peak for what
. A coalition in its classical sense is a peak of the cube T, or more precisely, that peak for what For a measure
For a measure 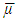 that concentrated on peaks
that concentrated on peaks 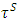 of the cube
of the cube 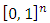 and accepts values
and accepts values 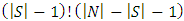 the expression for
the expression for 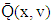 can be rewritten in a simpler form:
can be rewritten in a simpler form: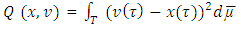 On the cube T instead of
On the cube T instead of 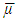 one can take an arbitrary measure and define the value
one can take an arbitrary measure and define the value 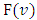 for a game
for a game 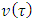 as a point on what the newly obtained functional
as a point on what the newly obtained functional 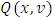 will reach its minimum.Farther we will choose a measure such that the function
will reach its minimum.Farther we will choose a measure such that the function 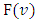 would possess with properties defined by axioms, similar to Shapley axioms for classical cooperative games.Below formulated analogs of Shapley axioms for fuzzy cooperative games.A1 (Symmetry) Let π is an injection from the set
would possess with properties defined by axioms, similar to Shapley axioms for classical cooperative games.Below formulated analogs of Shapley axioms for fuzzy cooperative games.A1 (Symmetry) Let π is an injection from the set 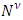 on
on 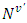 such, that for each coalition
such, that for each coalition 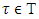
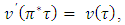 where
where 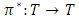 is a map, for what
is a map, for what 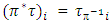 .Then, for all
.Then, for all 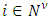
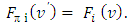 A.2 (Pareto optimality)
A.2 (Pareto optimality)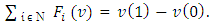 The unusual form of this axiom compared with its classical analogue caused by the fact that the possibility of
The unusual form of this axiom compared with its classical analogue caused by the fact that the possibility of 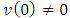 not excluded.A.3 (Inefficiency of ‘dummy’) If in the game
not excluded.A.3 (Inefficiency of ‘dummy’) If in the game 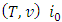 is a player such, that
is a player such, that 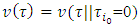 , for arbitrary
, for arbitrary 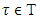 , then
, then 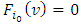 . The expression
. The expression 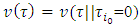 means, that the value of the coalition
means, that the value of the coalition 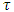 in the game
in the game 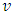 equals to the same value for the coalition with
equals to the same value for the coalition with 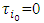 .A.4 (Aggregation) If
.A.4 (Aggregation) If 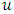 and
and 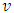 are games with the same set of coalitions T and
are games with the same set of coalitions T and 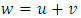 , then
, then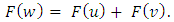 Besides A.3 we will also deal with its strengthened form. There will be a need for the next definition.Definition 1. We will say that the game
Besides A.3 we will also deal with its strengthened form. There will be a need for the next definition.Definition 1. We will say that the game 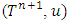 derived from the game
derived from the game 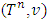 by adding to it a ‘dummy’ player
by adding to it a ‘dummy’ player 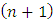 , if for every coalition
, if for every coalition 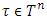 and every
and every 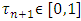 takes place:
takes place: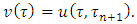 A3’. (The strengthened axiom of ‘dummy’) Holds true
A3’. (The strengthened axiom of ‘dummy’) Holds true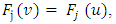 for arbitrary
for arbitrary 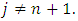 The A3’ otherwise, means that including a ‘dummy’ in a game does not change gains of other players.It is obvious, that if A.2 remains true, then the A.3 follows from A.3’.In general the choice of measure µ is not unique. Partially as such a measure can be also
The A3’ otherwise, means that including a ‘dummy’ in a game does not change gains of other players.It is obvious, that if A.2 remains true, then the A.3 follows from A.3’.In general the choice of measure µ is not unique. Partially as such a measure can be also 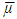 . The axiom A.1 holds true, if the measure has been defined the same way on all of the sides of the cube.Let now consider the following sets. For arbitrary
. The axiom A.1 holds true, if the measure has been defined the same way on all of the sides of the cube.Let now consider the following sets. For arbitrary 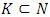 and
and 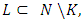 denote by
denote by 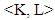 the following set:
the following set: 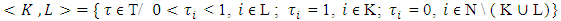
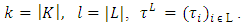 Sets <K, L> actually are the faces of the cube
Sets <K, L> actually are the faces of the cube 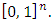 We will deal with the case, when on each one of its faces measure defined by a density function
We will deal with the case, when on each one of its faces measure defined by a density function 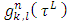 . To satisfy axiom A.1 will be accepted that
. To satisfy axiom A.1 will be accepted that 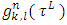 are symmetric, none negative functions of their arguments. As a result, we will have the following functional:
are symmetric, none negative functions of their arguments. As a result, we will have the following functional: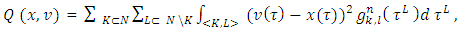 where
where 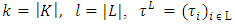 .Our goal is finding relations between the functions
.Our goal is finding relations between the functions 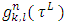 so that the function
so that the function 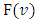 which minimizes functional
which minimizes functional 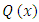 , has satisfied to axioms A.3 and A.3’.
, has satisfied to axioms A.3 and A.3’.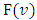 , which minimizes functional
, which minimizes functional 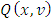 . At the same time for functions
. At the same time for functions 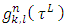 participating in the expression of functional
participating in the expression of functional 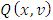 , we will formulate requirements so that with them hold true the Shapley axioms for
, we will formulate requirements so that with them hold true the Shapley axioms for 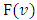 .Farther we will use the defined below magnitudes:
.Farther we will use the defined below magnitudes: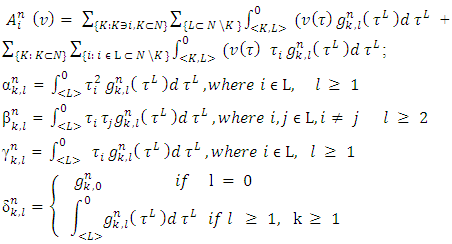 Let extend definitions of
Let extend definitions of 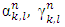 for
for 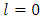 and
and 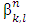 for
for 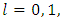 by accepting that
by accepting that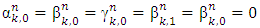 . Besides, let also accept that
. Besides, let also accept that 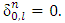 Further we will need to deal with numbers:
Further we will need to deal with numbers: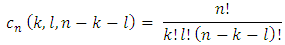 We denote:
We denote: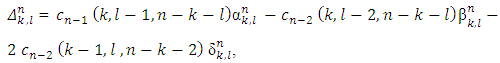 and
and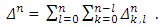 Preposition 1. If
Preposition 1. If 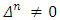 , then the functional Q(x, v) on the set
, then the functional Q(x, v) on the set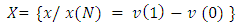 its minimum by x accepts on the vector
its minimum by x accepts on the vector 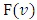 with following components:
with following components: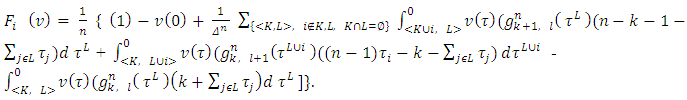
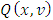 reaches its minimum, according to the method of Lagrange’s multipliers should satisfy to the following system of linear equations:
reaches its minimum, according to the method of Lagrange’s multipliers should satisfy to the following system of linear equations: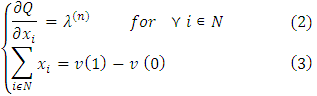 To write these equations in explicit form we need to find the partial differentials of
To write these equations in explicit form we need to find the partial differentials of 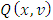 :
: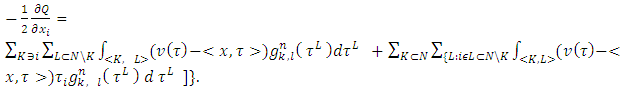 There will be need as well for the following notations:
There will be need as well for the following notations: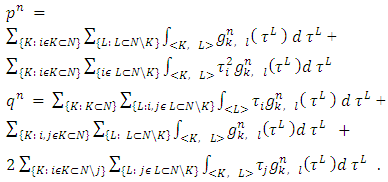 We need to prove that
We need to prove that 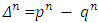 . So, let rewrite the expressions for
. So, let rewrite the expressions for 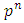 and
and 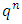 in different forms:
in different forms: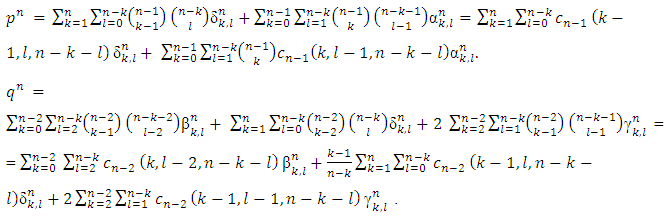 As far as above we redefined the magnitudes
As far as above we redefined the magnitudes 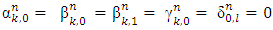 , so, while figuring out the difference
, so, while figuring out the difference 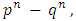 we can formally extend summing by the index k from 0 to n and by the index l from 0 to
we can formally extend summing by the index k from 0 to n and by the index l from 0 to 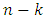 . That will result the required equality instantly.Further, by using the defined above notations we can rewrite (2) - (3) in an equivalent form:
. That will result the required equality instantly.Further, by using the defined above notations we can rewrite (2) - (3) in an equivalent form: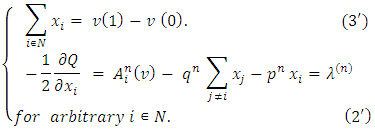 Summing equations (2’) by i and taking in account the (3’), we will obtain, that
Summing equations (2’) by i and taking in account the (3’), we will obtain, that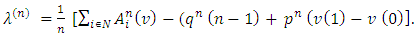 That expression for
That expression for 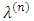 together with the system (2’) – (3’) gives:
together with the system (2’) – (3’) gives: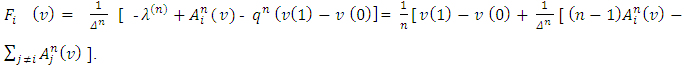 Submitting in this formula the expression for
Submitting in this formula the expression for 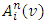 and uniting the integrals with coinciding domains of integration, we will have the following expression for
and uniting the integrals with coinciding domains of integration, we will have the following expression for 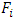
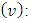
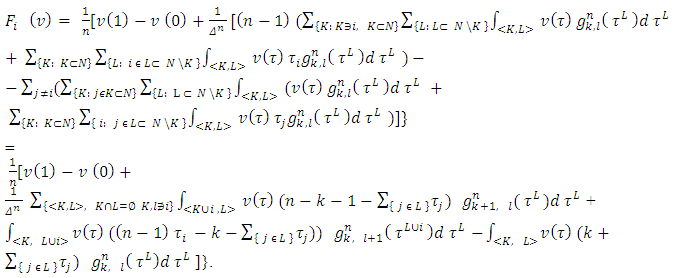 As a result we have obtained the required formula (2.1).Remark.1. In general the solution
As a result we have obtained the required formula (2.1).Remark.1. In general the solution 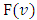 for system (2) - (3) is unique for arbitrary (and not only for not negative) functions
for system (2) - (3) is unique for arbitrary (and not only for not negative) functions 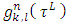 , which participate in
, which participate in 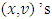 expression. The obtained that way solution for system (2) - (3) still can be accepted as some analogue for the Shapley function, despite of that it already may not minimize the functional
expression. The obtained that way solution for system (2) - (3) still can be accepted as some analogue for the Shapley function, despite of that it already may not minimize the functional 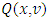 .Remark.2. For a functional
.Remark.2. For a functional 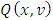 with arbitrary measure μ the
with arbitrary measure μ the 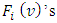 expression becomes much simpler. So let
expression becomes much simpler. So let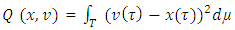 By using the following notations,
By using the following notations,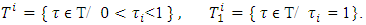 We can rewrite the expression for
We can rewrite the expression for 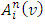 the following way:
the following way: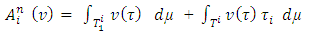 By submitting that expression for
By submitting that expression for 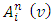 in the formula for
in the formula for 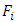
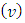 , we will have that
, we will have that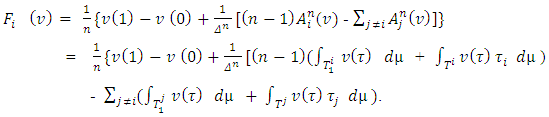
 . For the function
. For the function 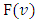 to satisfy axiom A3 it is necessary and sufficient, that hold true the following equations:
to satisfy axiom A3 it is necessary and sufficient, that hold true the following equations: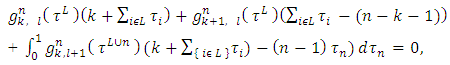
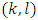 that
that  , besides
, besides 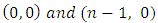 . In addition will also take place the following equations:
. In addition will also take place the following equations: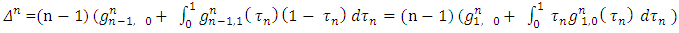
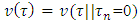 , for all
, for all 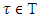 .The integral equations below take place due to the ‘dummies’ property:
.The integral equations below take place due to the ‘dummies’ property: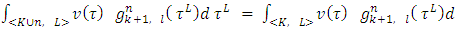
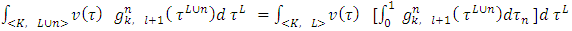
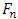
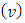 by using equalities (7) and (8), we will obtain the following expression:
by using equalities (7) and (8), we will obtain the following expression: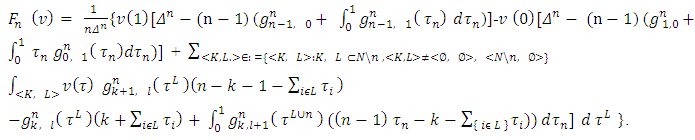
 based on the axiom A3. At the same time
based on the axiom A3. At the same time 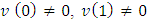 and
and 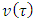 is for arbitrary coalition
is for arbitrary coalition 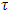 . From there, the expressions in square brackets should be equal to 0. Hence, as a result we will obtain the equations (5) and (6).To conclude it is remaining to show, that the equations (6) can be derived from (5), to what will be devoted the rest of the proof.Let consider the following magnitudes:
. From there, the expressions in square brackets should be equal to 0. Hence, as a result we will obtain the equations (5) and (6).To conclude it is remaining to show, that the equations (6) can be derived from (5), to what will be devoted the rest of the proof.Let consider the following magnitudes: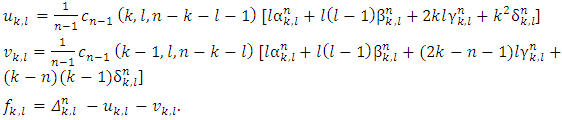
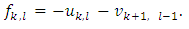
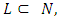 and
and 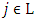 . We will consider the integral below:
. We will consider the integral below: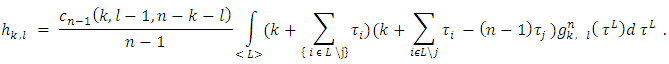 Let transform the sub integral expression by using the symmetry of functions
Let transform the sub integral expression by using the symmetry of functions 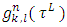 and invented in the beginning notations:
and invented in the beginning notations: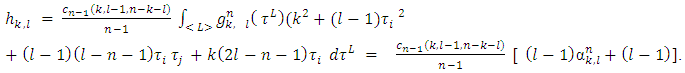 The expression below we will obtain by applying the condition (5) to the integral
The expression below we will obtain by applying the condition (5) to the integral 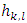 :
: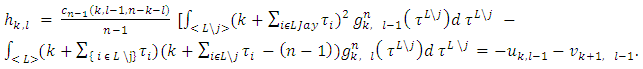 That is what has been required to prove.Lemma 2. For every
That is what has been required to prove.Lemma 2. For every 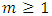 , takes place the following presentation:
, takes place the following presentation: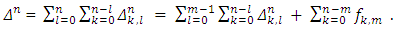
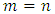 . Really, as far as
. Really, as far as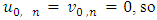
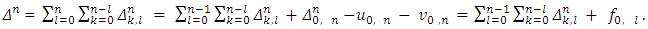 2. Accept that the expression (12) is correct for arbitrary m. We will use the formula (11) of the Lemma 1, as well as the equalities:
2. Accept that the expression (12) is correct for arbitrary m. We will use the formula (11) of the Lemma 1, as well as the equalities: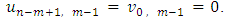 Below we have performed some quite natural transformations:
Below we have performed some quite natural transformations: 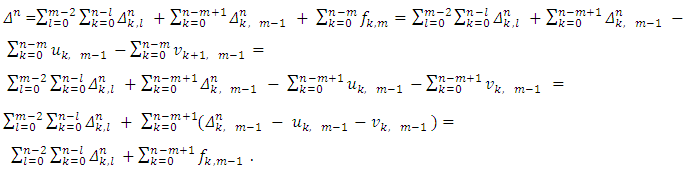 The lemma has been proved.
The lemma has been proved.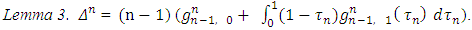 Proof. For
Proof. For 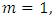 according to presentation from the Lemma 2,
according to presentation from the Lemma 2,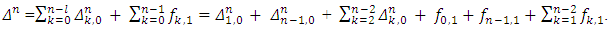 Based on formulas (11) and (10),
Based on formulas (11) and (10),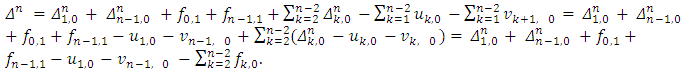 Let submit in the obtained expression submit values for the following magnitudes:
Let submit in the obtained expression submit values for the following magnitudes: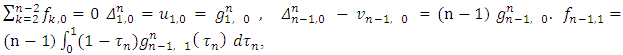 We will have the final expression
We will have the final expression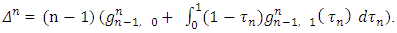
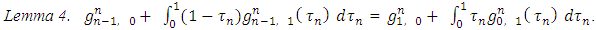 Proof. Below we are integrating the equality (5) by the domain
Proof. Below we are integrating the equality (5) by the domain 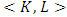 and using the notations above:
and using the notations above: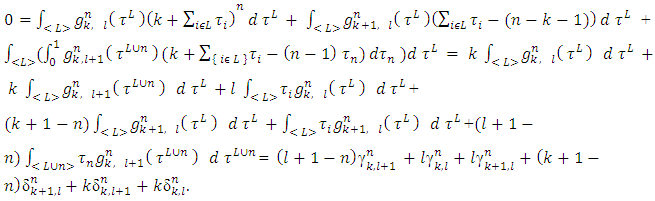 If to multiply the equalities above by
If to multiply the equalities above by 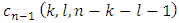 and sum them by all pairs
and sum them by all pairs 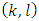 ,for what takes place the (5), then we will obtain:
,for what takes place the (5), then we will obtain: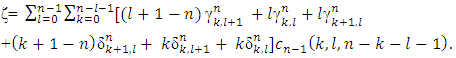 As far as
As far as 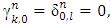 so we will have, that
so we will have, that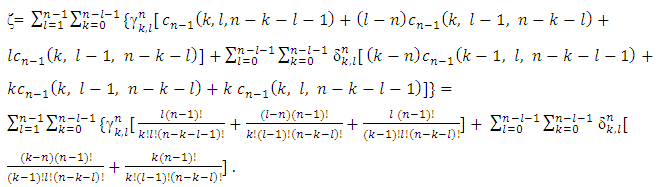 Expressions in the square brackets are equal to each other:
Expressions in the square brackets are equal to each other: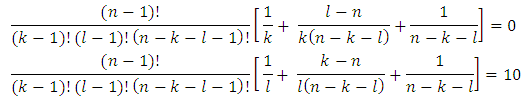 As a result
As a result 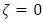 .Now recall that (5) takes place for pairs
.Now recall that (5) takes place for pairs 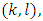 where that
where that 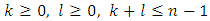 , besides the pairs
, besides the pairs 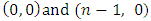 .If in the written above expression to separate from the sum members that correspond to pairs
.If in the written above expression to separate from the sum members that correspond to pairs 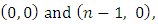 then based on (5) the remaining will be equal to 0.The separated members will give us the following expression:
then based on (5) the remaining will be equal to 0.The separated members will give us the following expression: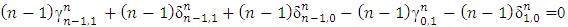 By substituting the values for participating magnitudes, we will obtain what has been required:
By substituting the values for participating magnitudes, we will obtain what has been required: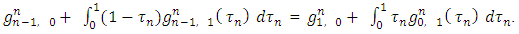 The last two lemmas conclude the proof of preposition 2.
The last two lemmas conclude the proof of preposition 2. be the pre-value for the game
be the pre-value for the game 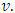 That means, it is the point on what the functional
That means, it is the point on what the functional 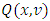 reaches its minimum, and participating in
reaches its minimum, and participating in 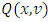 functions
functions 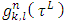 satisfy to the specified for
satisfy to the specified for 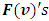 Shapley axioms conditions.In this paragraph we will show, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the prevalue
Shapley axioms conditions.In this paragraph we will show, that for a class of fuzzy games obtained from the classical cooperative games through the Owen’s multilinear extension, the prevalue 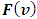 coincides with the Shapley prevalue for the classical game. Further, we will obtain necessary and sufficient conditions at what the function
coincides with the Shapley prevalue for the classical game. Further, we will obtain necessary and sufficient conditions at what the function 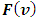 satisfies to the strengthened dummies axiom. We will also prove a preposition allowing constructing functions
satisfies to the strengthened dummies axiom. We will also prove a preposition allowing constructing functions 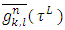 that satisfy to the axiom
that satisfy to the axiom 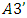 for fewer players.4.1. Fuzzy games we are going to deal with defined through certain n dimensional distribution functions
for fewer players.4.1. Fuzzy games we are going to deal with defined through certain n dimensional distribution functions 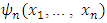 , that are continuous by each one of their arguments and satisfy to following condition:
, that are continuous by each one of their arguments and satisfy to following condition: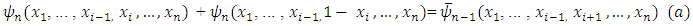 where
where 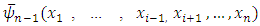 is some
is some 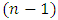 dimensional distribution function of variables
dimensional distribution function of variables 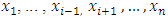 and possesses with the same kind of properties as functions
and possesses with the same kind of properties as functions 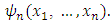 Preposition 3. Let
Preposition 3. Let 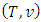 is a fuzzy game that obtained from a classical game
is a fuzzy game that obtained from a classical game 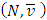 by the following way:
by the following way: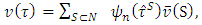
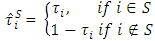 and
and 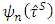 is a function that satisfies to the condition
is a function that satisfies to the condition 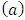 . If
. If 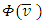 is the Shapley prevalue for game
is the Shapley prevalue for game 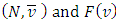 the prevalue for fuzzy game
the prevalue for fuzzy game 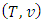 then
then 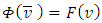 .Proof. Let
.Proof. Let 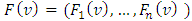 is the solution for system
is the solution for system 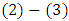 of game
of game 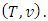 By using the explicit expression (4) for
By using the explicit expression (4) for 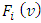 and formula (13) we can prove that
and formula (13) we can prove that 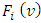 allows some linear representation that depends on
allows some linear representation that depends on 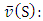
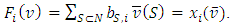
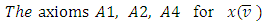 hold true due to properties of
hold true due to properties of 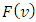 . So to prove our statement, we need to show, that for
. So to prove our statement, we need to show, that for 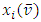 (takes place the ‘dummies’ axiom. So, we need to prove that if a player
(takes place the ‘dummies’ axiom. So, we need to prove that if a player 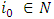 is a dummy in the game
is a dummy in the game 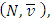 then
then 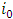 is so also in
is so also in 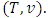 Let for all
Let for all 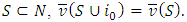 Then
Then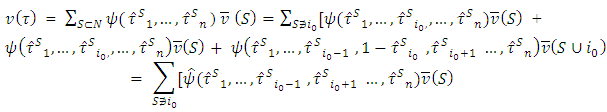 By the other side:
By the other side: 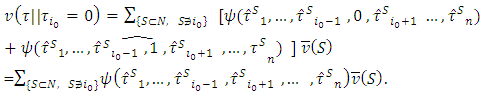 From there
From there 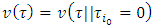 , and hence,
, and hence, 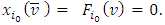 As a result we have obtained that the prevalue
As a result we have obtained that the prevalue 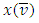 satisfies to all of the Shapley axioms, which means, that
satisfies to all of the Shapley axioms, which means, that 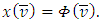 Remark. In a special case, when players participate in coalition independently of each other, i.e., when
Remark. In a special case, when players participate in coalition independently of each other, i.e., when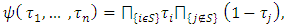 then
then 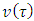 is a multilinear extension of Owen. One can check it easily, that then for functions
is a multilinear extension of Owen. One can check it easily, that then for functions 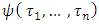 takes place the condition
takes place the condition 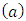 .Below we will derive relations that concern to the strengthened axiom of ‘dummy’.Preposition 4. Let
.Below we will derive relations that concern to the strengthened axiom of ‘dummy’.Preposition 4. Let 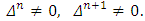 The function
The function 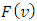 in an
in an 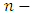 person game satisfies to the strengthened ‘dummies’ axiom if and only if, when for all such pairs
person game satisfies to the strengthened ‘dummies’ axiom if and only if, when for all such pairs 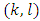 that
that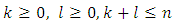 , besides the
, besides the 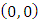 and
and 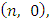 takes place the following equation:
takes place the following equation: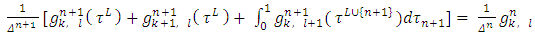
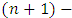 players game:
players game: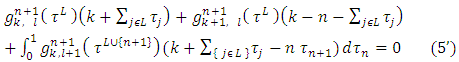 Proof. Necessity. The equation
Proof. Necessity. The equation 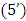 follows from the Proposition2, because, if the axiom A2. holds true, then A3 follows from the A3’.The same way, as we did it in case of formula (2.1), let again write the expression for
follows from the Proposition2, because, if the axiom A2. holds true, then A3 follows from the A3’.The same way, as we did it in case of formula (2.1), let again write the expression for 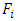
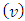 by separating the player
by separating the player 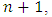 while summing by the side
while summing by the side 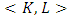 of the cube and replacing
of the cube and replacing 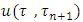 by
by 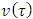 , based on the equation
, based on the equation 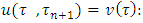
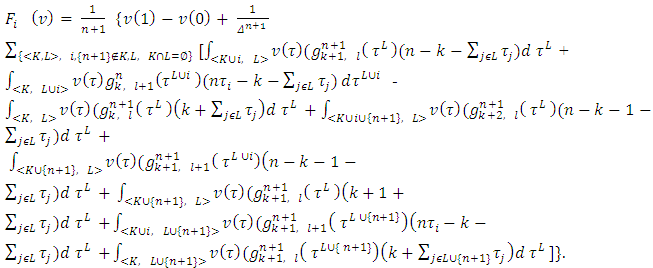

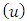 . According to the strengthened axiom of ‘dummy’, gains for the same player
. According to the strengthened axiom of ‘dummy’, gains for the same player 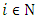 in both of the games
in both of the games 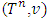 and
and 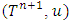 are the same. That is the reason because of what the obtained for
are the same. That is the reason because of what the obtained for 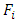
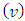 and
and 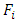
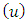 expressions are equal. Let write that equation:
expressions are equal. Let write that equation: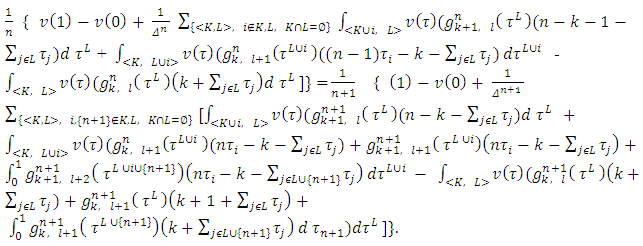 By equalizing coefficients at
By equalizing coefficients at 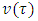 for similar coalitions in both of the sides of equation we will obtain relations that connect functions
for similar coalitions in both of the sides of equation we will obtain relations that connect functions 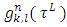 and
and 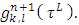 Forms of the mentioned coefficients depend on the cubes sides to what coalition
Forms of the mentioned coefficients depend on the cubes sides to what coalition 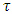 belongs. More precisely, to which one of the sets
belongs. More precisely, to which one of the sets 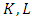 or
or 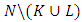 belongs the player i. Besides that special views have the coefficients at
belongs the player i. Besides that special views have the coefficients at 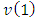 and
and 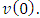 As a result we will have, that the equality
As a result we will have, that the equality 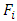
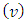 =
= 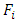
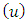 (i.e. the axiom A3’) is equivalent to the following five relations.The equality of coefficients at
(i.e. the axiom A3’) is equivalent to the following five relations.The equality of coefficients at 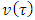 for
for 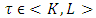 , where
, where 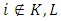 (besides the side
(besides the side  ) gives as the relation:
) gives as the relation: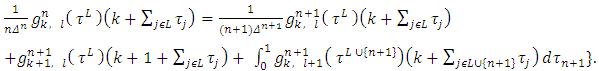
 that
that  , besides the pair
, besides the pair 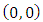 .For the sides
.For the sides 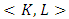 , where
, where  besides the side
besides the side 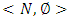 , we will obtain the following relation:
, we will obtain the following relation: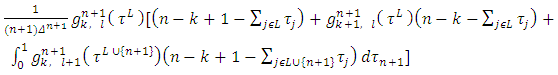
 that
that  , besides the pair
, besides the pair  .For the sides
.For the sides 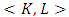 , where
, where 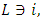 we will obtain the following relation:
we will obtain the following relation: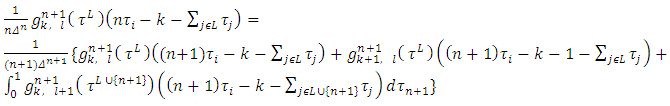
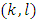 that
that 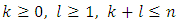 .Finally, by equalizing the coefficients at
.Finally, by equalizing the coefficients at 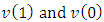 we will obtain
we will obtain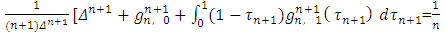
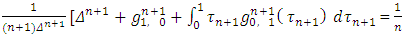
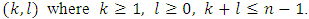 Adding to each other equalities (16) and (18) and dividing the sum by
Adding to each other equalities (16) and (18) and dividing the sum by 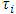 we will obtain that (14) takes place for pairs
we will obtain that (14) takes place for pairs 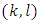 where
where 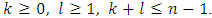 Subtracting from each other the equalities (16) and (18) and dividing the result by
Subtracting from each other the equalities (16) and (18) and dividing the result by 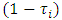 we will have that (14) takes place for pairs
we will have that (14) takes place for pairs 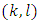 , where
, where 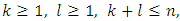 besides the pair
besides the pair 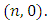 So, we have proved that the equality (14) takes place for all pairs
So, we have proved that the equality (14) takes place for all pairs 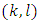 that
that 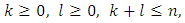 besides the pairs
besides the pairs 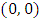 and
and 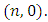 The Proposition takes place for pairs
The Proposition takes place for pairs 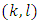 , where has been proved fully.Below proved one more proposition that allows constructing functions
, where has been proved fully.Below proved one more proposition that allows constructing functions 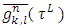 such that for
such that for 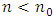 satisfy equations (5) if they do the same for
satisfy equations (5) if they do the same for 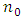 .Proposition 5. Let for some
.Proposition 5. Let for some 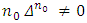 and for functions
and for functions 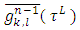 ,
,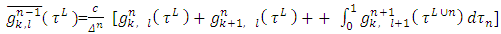
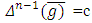 and functions
and functions 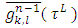 satisfy to the equation (5) too.Proof. The equation
satisfy to the equation (5) too.Proof. The equation 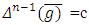 can be proved by using equations (21) and the known earlier formula, but this time for
can be proved by using equations (21) and the known earlier formula, but this time for 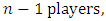 i.e.
i.e.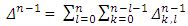 To check that functions
To check that functions 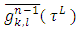 satisfy (5) it is enough using the formula (21) to figure out taking part in (5) magnitudes that written for (n−1), and after that summing them by taking in account that the (5) takes place for the n −game.3. Below are examples for the sets of none negative functions that satisfy to ‘dummies’ axiom in case of some fixed number of players n.Example 1. Simplest is the set of functions
satisfy (5) it is enough using the formula (21) to figure out taking part in (5) magnitudes that written for (n−1), and after that summing them by taking in account that the (5) takes place for the n −game.3. Below are examples for the sets of none negative functions that satisfy to ‘dummies’ axiom in case of some fixed number of players n.Example 1. Simplest is the set of functions 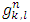 defined the following way:
defined the following way: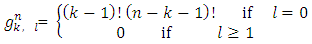 Gain of a player in case of defined functions depends only on game’s value on the peaks of cube
Gain of a player in case of defined functions depends only on game’s value on the peaks of cube 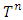 , which are the coalitions in the classical sense. The functional
, which are the coalitions in the classical sense. The functional 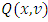 in its turn coincides with the functional
in its turn coincides with the functional 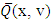 that defined for classical cooperative games.Example 2. Let for some n define functions
that defined for classical cooperative games.Example 2. Let for some n define functions 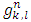 the following way:
the following way: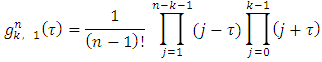
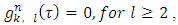 and by using the formula below recurrently define
and by using the formula below recurrently define 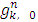 :
: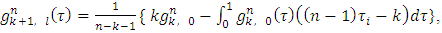 where one can choose
where one can choose 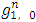 arbitrary, but big enough to get
arbitrary, but big enough to get 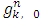 none negative.For l=0 equations (5) immediately follow from the formula that recurrently defines theFunctions
none negative.For l=0 equations (5) immediately follow from the formula that recurrently defines theFunctions 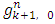 .For l=1 we have:
.For l=1 we have: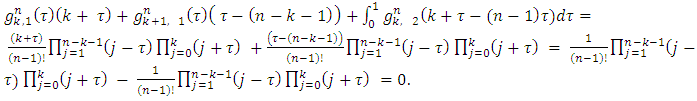 Further we will apply the Proposition 5, by accepting that
Further we will apply the Proposition 5, by accepting that 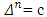 . Let check, that for
. Let check, that for 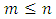 the functions
the functions 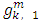 can be defined by the formula (21):
can be defined by the formula (21):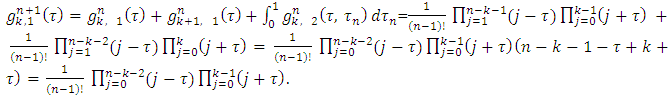 That way we have constructed example of functions
That way we have constructed example of functions 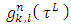 that satisfy to the axiom
that satisfy to the axiom 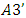 for some number of players n that does not succeed to certain
for some number of players n that does not succeed to certain 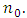 However, doing the same for arbitrary n this method unfortunately does not allow.We should mention, that in this example essential are only those coalitions, which get described by peaks and the line segments that connect adjacent peaks of cube
However, doing the same for arbitrary n this method unfortunately does not allow.We should mention, that in this example essential are only those coalitions, which get described by peaks and the line segments that connect adjacent peaks of cube 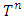 .Example 3. For
.Example 3. For 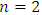 to axiom A3 satisfy the following functions that defined on square:
to axiom A3 satisfy the following functions that defined on square: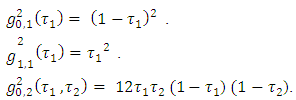 Remark 4. All of the functions
Remark 4. All of the functions 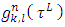 that constructed in examples above satisfy to the following condition:
that constructed in examples above satisfy to the following condition: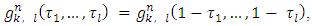 which can be considered as another property for the distribution functions
which can be considered as another property for the distribution functions 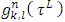 .As a conclusion the author would like to appreciate any information about copyright breach of these results.
.As a conclusion the author would like to appreciate any information about copyright breach of these results. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML