Alexander Munson
Division of Integrated Sciences, Wilson College, Chambersburg, PA, United States
Correspondence to: Alexander Munson, Division of Integrated Sciences, Wilson College, Chambersburg, PA, United States.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
We consider the question whether a pillage game can have infinitely many stable sets under certain regularity and dominance conditions. We establish a rigidity result in continuous pillage games. This property implies that in any continuous pillage game, an allocation's dominance structure is essentially determined by local regularity behaviours of the power function. Using this property, we derive a weak convergence theorem on the power set of the n-players near any point in the allocation space by passing any sequence of allocations through specially constructed filters subject to geometric, parity, and unidirectionality conditions. Combining these results, a sufficient condition for the theoretical existence of an infinite set of stable sets is proposed. We also discuss the extension of our results in the wider scope where some of the conditions are lifted.
Keywords:
Cooperative game theory, Pillage games, Stable set
Cite this paper: Alexander Munson, Cyclicity in Cooperative Games – A Theoretical Model for an Infinite Order of Stable Sets in Pillage Games, Journal of Game Theory, Vol. 8 No. 1, 2019, pp. 1-8. doi: 10.5923/j.jgt.20190801.01.
1. Introduction
Cooperative games require players to examine their individual strategies as well as to coordinate with other players to maximize the payoff of a subset of related players. These subsets give rise to the concept of coalitions. In pillage games which are a type of cooperative games, a coalition's strength is measured by its current possession of a given set of goods.As with other cooperative games, stable sets are a key interest. Conceptually, stable sets are locus of allocations for a coalition where once all the players in the coalition attain one such allocation of the goods, they suffer a loss in valuation determined by the power function against players outside of the coalition if one player unilaterally moves away from such allocation, i.e. a dynamic equilibrium is reached, similar to an attractor in a dynamical system. Jordan proved that the cardinality of any given stable set in continuous pillage games is finite [1]. McKenzie, Kerber and Rowat showed that the cardinality of an internally stable set is bounded above by 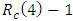 where
where 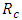 is the diagonal multicolor Ramsey number and c is the number of players in the game [2]. Examining strictly monotonic sequences in dimensions greater than 1, Saxton showed that
is the diagonal multicolor Ramsey number and c is the number of players in the game [2]. Examining strictly monotonic sequences in dimensions greater than 1, Saxton showed that 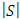 , the cardinality of a stable set in an n-player pillage game satisfies
, the cardinality of a stable set in an n-player pillage game satisfies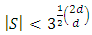 | (1) |
where 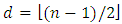 is the floor function [3]. Using measure theory, Beardon and Rowat was able to represent any internally stable set as a finite union of sets satisfying certain pairwise comparison conditions, thereby proving that a stable set's topological dimension in an n-player, m-good pillage game is bounded above by
is the floor function [3]. Using measure theory, Beardon and Rowat was able to represent any internally stable set as a finite union of sets satisfying certain pairwise comparison conditions, thereby proving that a stable set's topological dimension in an n-player, m-good pillage game is bounded above by 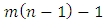 [4].These properties on stable sets prompted the question: can there be a pillage game with infinitely many stable sets, namely is there a pillage game where the collection of stable set is of order
[4].These properties on stable sets prompted the question: can there be a pillage game with infinitely many stable sets, namely is there a pillage game where the collection of stable set is of order 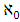 or greater? This question is significant in cooperative games. Historically, Shapley found examples of cooperative games that have infinitely many stable sets by using characteristic functions [5]. In pillage games, McKenzie, Kerber, and Rowat constructed an example of a pillage game with multiple independent stable sets [2]. Thus the above question deserves some serious consideration. In this paper, we give a partial answer to this question. We consider the case of a single good continuous pillage game with non-empty core under a forward dominance structure. We examine a theoretical model of a continuous pillage game satisfying the forward dominance condition. The creation of a concrete model depends on a function satisfying the numerical constraints that permits these conditions. Examples will be given in this paper, we defer the task of finding a concrete example satisfying the many numerical properties set forth in his paper since such a concrete example requires the careful coding by a computer language specialist who encodes these properties in an algorithm and tests it on a work station with sufficient computing power to effect such concrete examples. As such, the primary contribution of this paper is theoretical. The format of this paper is as follows: section 2 of the paper gives the basic background of pillage games. Section 3 introduces a basic property of continuous pillage games - a rigidity theorem. This theorem gives the local structure of dominance in an infinite sequence of allocations as it approaches its limit point. In section 4, using the rigidity theorem, we establish a weak convergence theorem on the dominance structure of any sequence of allocations by using ultrafilters that select subsequences based on geometric properties, unidirectionality conditions, and parity comparison conditions. In section 5, we combine the above results to show a theoretical model in which a set of sufficient conditions for an infinite set of stable sets exists under a cyclic forward dominance structure.In the discussions of section 6, we provide a possible future approach to the study of pillage games and indeed cooperative games in general by highlighting certain fibre bundle properties embedded in pillage games and the possibility of a representation theorem for power functions. The fibre bundle properties are a signature property satisfied by pillage games without the requirement of continuity. Fibre bundles considerations are connected to measure-theoretic integrations in the broader sense. Integration over the base in a fibre bundle points to a representation theorem for pillage games similar to the Riesz representation theorem in classical functional analysis. As a result, fundamental questions in these games such as dominance, stability, and power dynamics among coalitions can be examined through questions about their respective fibre-theoretic analogues such as minimax plateau studies, fibre neighbourhood investigations, and local-global duality studies on function spaces over the fibre bases.
or greater? This question is significant in cooperative games. Historically, Shapley found examples of cooperative games that have infinitely many stable sets by using characteristic functions [5]. In pillage games, McKenzie, Kerber, and Rowat constructed an example of a pillage game with multiple independent stable sets [2]. Thus the above question deserves some serious consideration. In this paper, we give a partial answer to this question. We consider the case of a single good continuous pillage game with non-empty core under a forward dominance structure. We examine a theoretical model of a continuous pillage game satisfying the forward dominance condition. The creation of a concrete model depends on a function satisfying the numerical constraints that permits these conditions. Examples will be given in this paper, we defer the task of finding a concrete example satisfying the many numerical properties set forth in his paper since such a concrete example requires the careful coding by a computer language specialist who encodes these properties in an algorithm and tests it on a work station with sufficient computing power to effect such concrete examples. As such, the primary contribution of this paper is theoretical. The format of this paper is as follows: section 2 of the paper gives the basic background of pillage games. Section 3 introduces a basic property of continuous pillage games - a rigidity theorem. This theorem gives the local structure of dominance in an infinite sequence of allocations as it approaches its limit point. In section 4, using the rigidity theorem, we establish a weak convergence theorem on the dominance structure of any sequence of allocations by using ultrafilters that select subsequences based on geometric properties, unidirectionality conditions, and parity comparison conditions. In section 5, we combine the above results to show a theoretical model in which a set of sufficient conditions for an infinite set of stable sets exists under a cyclic forward dominance structure.In the discussions of section 6, we provide a possible future approach to the study of pillage games and indeed cooperative games in general by highlighting certain fibre bundle properties embedded in pillage games and the possibility of a representation theorem for power functions. The fibre bundle properties are a signature property satisfied by pillage games without the requirement of continuity. Fibre bundles considerations are connected to measure-theoretic integrations in the broader sense. Integration over the base in a fibre bundle points to a representation theorem for pillage games similar to the Riesz representation theorem in classical functional analysis. As a result, fundamental questions in these games such as dominance, stability, and power dynamics among coalitions can be examined through questions about their respective fibre-theoretic analogues such as minimax plateau studies, fibre neighbourhood investigations, and local-global duality studies on function spaces over the fibre bases.
2. Fundamentals of Pillage Games
A single good n-player pillage game is a game among the set I of the n players 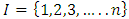 dividing a single good/commodity where the players' shares of the good are represented as vectors in the convex hull X with vertex at unity on each of the n axes in
dividing a single good/commodity where the players' shares of the good are represented as vectors in the convex hull X with vertex at unity on each of the n axes in 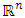 :
: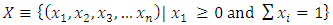 | (2) |
Each element 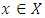 is called an allocation of the good. Given an allocation x, its utility with respect to a subset of players
is called an allocation of the good. Given an allocation x, its utility with respect to a subset of players 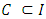 is measured by a real-valued function called the power function
is measured by a real-valued function called the power function 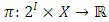 satisfying the three order axioms:
satisfying the three order axioms: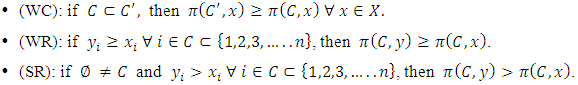 The notation
The notation 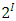 denotes the power set of the n players. Thus a pillage game is a triple
denotes the power set of the n players. Thus a pillage game is a triple 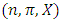 with the above properties. If there is the additional requirement that for each
with the above properties. If there is the additional requirement that for each 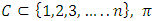 is continuous on the allocation variable x, then we call
is continuous on the allocation variable x, then we call 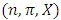 a continuous pillage game.An allocation a dominates another allocation b, denoted as
a continuous pillage game.An allocation a dominates another allocation b, denoted as 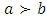 if
if 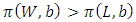 where
where 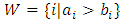 and
and 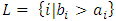 . We call W the win set and L the lose set. The idea of dominance measured by the power function is that given an allocation, a more dominant player can move toward another allocation that confers higher utility. The power function therefore both informs and is informed by the allocation structures. Thus its properties are of critical interest in pillage games.Given
. We call W the win set and L the lose set. The idea of dominance measured by the power function is that given an allocation, a more dominant player can move toward another allocation that confers higher utility. The power function therefore both informs and is informed by the allocation structures. Thus its properties are of critical interest in pillage games.Given 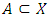 , the dominion of A, denoted as
, the dominion of A, denoted as 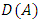 is the set of allocations that are dominated by some element of
is the set of allocations that are dominated by some element of 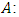
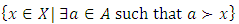 . Thus
. Thus 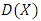 is the set of allocations that are dominated by at least one other allocation. The core, denoted as K, is the set of un-dominated allocations, i.e.
is the set of allocations that are dominated by at least one other allocation. The core, denoted as K, is the set of un-dominated allocations, i.e. 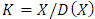 . A set A is said to satisfy internal stability if dominance does not occur between allocations of
. A set A is said to satisfy internal stability if dominance does not occur between allocations of 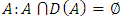 . Clearly the core K is both internally stable and contained in any internally stable set. A is said to satisfy external stability if
. Clearly the core K is both internally stable and contained in any internally stable set. A is said to satisfy external stability if 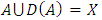 . A set A is called a stable set if it satisfies both internal and external stability. Jordan showed that an internally stable set of a pillage game can contain only finitely many allocations [1].
. A set A is called a stable set if it satisfies both internal and external stability. Jordan showed that an internally stable set of a pillage game can contain only finitely many allocations [1].
3. A Rigidity Theorem
Let 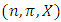 be a continuous pillage game. Let
be a continuous pillage game. Let 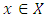 be an allocation. If A and B are two non-empty and non-intersecting subsets of
be an allocation. If A and B are two non-empty and non-intersecting subsets of 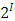 , then the power function can assume any of the following 3 all-inclusive but mutually exclusive relations on A and B at x:
, then the power function can assume any of the following 3 all-inclusive but mutually exclusive relations on A and B at x: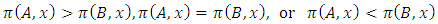 Definition 1. Let x be an allocation in a continuous pillage game
Definition 1. Let x be an allocation in a continuous pillage game 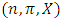 .(1) Let
.(1) Let 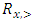 denote the set of all non-empty and non-intersecting pairs of sets
denote the set of all non-empty and non-intersecting pairs of sets 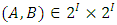 such that
such that 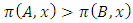 .(2) Similarly, let
.(2) Similarly, let 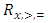 denote the set of all non-empty and non-intersecting pairs of sets
denote the set of all non-empty and non-intersecting pairs of sets 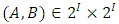 such that
such that 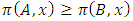 .Theorem 1. Given a continuous pillage game
.Theorem 1. Given a continuous pillage game 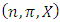 , let
, let 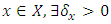 such that
such that 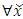 with
with 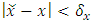 , we have
, we have 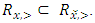 Here
Here 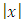 is the Euclidean norm on
is the Euclidean norm on 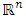 .Proof. We examine the disjoints sets
.Proof. We examine the disjoints sets 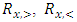 , and
, and 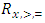 . Let
. Let 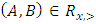 , by definition,
, by definition, 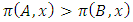 . Denote
. Denote 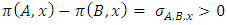 . Notice
. Notice 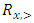 is a finite set because the power set
is a finite set because the power set 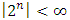 . In fact
. In fact 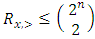 | (3) |
Assume without the loss of generality that 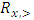 has cardinality m:
has cardinality m: 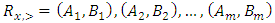 . We also have the corresponding
. We also have the corresponding 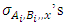 , one for each pair of
, one for each pair of 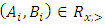 . The continuity of
. The continuity of  means that the power function
means that the power function 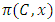 is continuous on the allocation variable x given a fixed set
is continuous on the allocation variable x given a fixed set 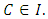 This implies for any
This implies for any 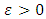 , there is a
, there is a 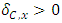 such that
such that 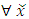 with
with 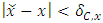 , we have
, we have 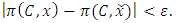 One needs take caution that given an x and an
One needs take caution that given an x and an 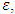 unless uniform continuity is assumed, different subsets of
unless uniform continuity is assumed, different subsets of 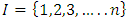 will require different
will require different 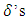 , one for each subset
, one for each subset 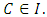 Let
Let 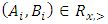 , as before, we have
, as before, we have 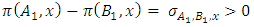 . Thus we have
. Thus we have 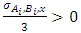 | (4) |
By the continuity of the power function 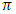 , we choose two neighborhoods: a
, we choose two neighborhoods: a 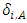 -neighbourhood for the set
-neighbourhood for the set 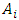 and a
and a 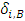 -neighbourhood for the set
-neighbourhood for the set 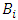 such that
such that 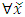 with
with 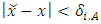 and
and 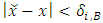 we have
we have 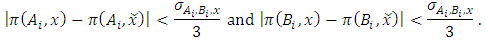 Let
Let 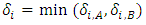 , then for all
, then for all 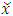 with
with 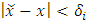 , we have
, we have 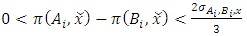 | (5) |
This means for any 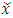 within a small neighborhood of x, if
within a small neighborhood of x, if 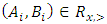 , then
, then 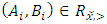 . There are only finitely many pairs of sets
. There are only finitely many pairs of sets 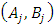 in
in 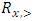 . Each pair
. Each pair 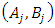 has a corresponding
has a corresponding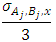 and a corresponding
and a corresponding 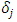 . To extend the above inclusion to all pairs of sets
. To extend the above inclusion to all pairs of sets 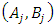 in
in 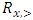 , we define
, we define 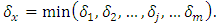 Then for all
Then for all 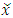 with
with 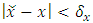 and for all
and for all 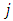 with
with 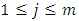 , we have
, we have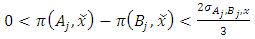 | (6) |
Thus within a sufficiently small neighbourhood, we have the set inclusion 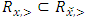 . This completes the proof. This theorem implies that the dominance structure at a point is informed or “bounded” by a larger set of dominance structures of the points in a small neighbourhood near that point. In the next section, we will examine the case of a set of infinitely many allocations under a forward dominance structure. The theorem above will create certain useful properties in a special subset of these allocations.
. This completes the proof. This theorem implies that the dominance structure at a point is informed or “bounded” by a larger set of dominance structures of the points in a small neighbourhood near that point. In the next section, we will examine the case of a set of infinitely many allocations under a forward dominance structure. The theorem above will create certain useful properties in a special subset of these allocations.
4. Weak Convergence of Dominance
In this section, we will first examine a simple geometric property of the space X of allocations based on compactness. With this property, we will then examine its implications in the case of an infinite set of allocations sets 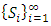 and derive a convergent theorem on the dominance structures. Jordan proved that the cardinality of a stable set in a pillage game is finite [1]. Thus if an infinite set of stable sets is possible in a pillage game with non-empty core K, each stable set must have finite cardinality and each
and derive a convergent theorem on the dominance structures. Jordan proved that the cardinality of a stable set in a pillage game is finite [1]. Thus if an infinite set of stable sets is possible in a pillage game with non-empty core K, each stable set must have finite cardinality and each 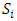 must contain at least one non-core allocation
must contain at least one non-core allocation 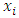 .Since
.Since 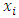 is not in the core, it is dominated by some other allocations. To achieve external stability, each stable set
is not in the core, it is dominated by some other allocations. To achieve external stability, each stable set 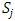 with
with 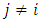 must contain at least one allocation that dominates
must contain at least one allocation that dominates 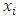 . Conversely,
. Conversely, 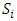 must also contain elements that dominate
must also contain elements that dominate 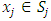 . To maintain internal stability, none of the elements that dominate
. To maintain internal stability, none of the elements that dominate 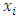 can be in
can be in 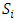 . In particular,
. In particular, 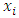 cannot be dominated by any core element. The Jordan finiteness theorem means that each stable set
cannot be dominated by any core element. The Jordan finiteness theorem means that each stable set 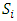 must achieve external stability
must achieve external stability 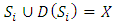 with only finitely many elements. Denote this set of non-core allocations in
with only finitely many elements. Denote this set of non-core allocations in 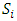 by
by 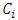 . Together these two conditions imply that if a continuous pillage game with non-empty core has infinitely many stable sets, each stable set
. Together these two conditions imply that if a continuous pillage game with non-empty core has infinitely many stable sets, each stable set 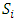 must contain a finite set
must contain a finite set 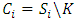 with
with 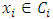 and
and 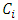 must contain allocations that dominate
must contain allocations that dominate 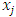 for all
for all 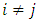 . With the above observations, we prove an immediate property of these pillage games. Theorem 2. If a continuous pillage game
. With the above observations, we prove an immediate property of these pillage games. Theorem 2. If a continuous pillage game 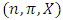 with infinitely many stable sets
with infinitely many stable sets 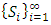 described above exists, then each
described above exists, then each 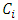 contains at least two allocations.Proof. Given two distinct stable sets
contains at least two allocations.Proof. Given two distinct stable sets 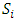 and
and 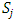 in this setup, to satisfy external stability,
in this setup, to satisfy external stability, 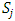 must contain a non-core element in
must contain a non-core element in 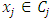 to dominate
to dominate 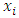 . In turn,
. In turn, 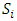 must contain a second element
must contain a second element 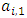 that dominates
that dominates 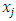 to achieve external stability. Furthermore,
to achieve external stability. Furthermore, 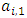 cannot be a core element because
cannot be a core element because 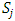 contains the same core K as
contains the same core K as 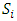 and
and 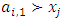 violates internal stability for the stable set
violates internal stability for the stable set 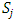 . So there are at least two allocations
. So there are at least two allocations 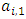 and
and 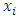 in
in 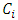 . A symmetric argument shows that
. A symmetric argument shows that 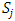 must also contain at least two elements. This completes the proof. Notice since
must also contain at least two elements. This completes the proof. Notice since 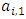 is not in the core, it must also be dominated by some non-core allocations in
is not in the core, it must also be dominated by some non-core allocations in 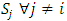 for
for 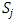 to achieve external stability. Therefore when the non-core elements of
to achieve external stability. Therefore when the non-core elements of 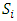 and
and 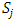 are compared, there is a chain of dominance between these allocations. External stability of each stable set implies that any chain of dominance between allocations from two stable sets, starting with a non-core allocation in
are compared, there is a chain of dominance between these allocations. External stability of each stable set implies that any chain of dominance between allocations from two stable sets, starting with a non-core allocation in 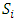 must also end with a non-core allocation in
must also end with a non-core allocation in 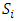 . A symmetric argument shows that this is also true if we start with a non-core allocation in
. A symmetric argument shows that this is also true if we start with a non-core allocation in 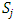 against
against 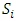 . The finiteness condition along with the above analysis implies a structural necessity for
. The finiteness condition along with the above analysis implies a structural necessity for 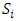 : since card
: since card 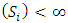 , each non-core allocation in
, each non-core allocation in 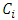 must complete a dominance loop of finite length which also ends with an allocation in
must complete a dominance loop of finite length which also ends with an allocation in 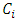 to achieve external stability. Therefore, there is a cyclicity in the dominance structure. This cyclicity allows closure in the sense that a chain starting with a non-core element in one stable set must return upon the same stable set when compared with the non-core elements in anther stable set. Thus a model of pillage game with infinite stable sets must have this cyclic closure property. Once this is achieved, the logical impossibility of a dominance loop never returning to itself is removed. The remaining work is to find a specific function with the numerical characteristics that satisfies the above mentioned cyclic dominance structure conditions. Consider a continuous pillage game
to achieve external stability. Therefore, there is a cyclicity in the dominance structure. This cyclicity allows closure in the sense that a chain starting with a non-core element in one stable set must return upon the same stable set when compared with the non-core elements in anther stable set. Thus a model of pillage game with infinite stable sets must have this cyclic closure property. Once this is achieved, the logical impossibility of a dominance loop never returning to itself is removed. The remaining work is to find a specific function with the numerical characteristics that satisfies the above mentioned cyclic dominance structure conditions. Consider a continuous pillage game 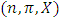 with non-empty core K. Let
with non-empty core K. Let 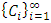 be a countably infinite set of allocations sets, each with finite cardinality. We can find a non-degenerate infinite sequence of allocations
be a countably infinite set of allocations sets, each with finite cardinality. We can find a non-degenerate infinite sequence of allocations 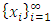 with
with 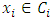 for each i. Since the total space of allocations X is compact, any non-degenerate infinite sequence in X contains a non-degenerate convergent subsequence. By an abuse of notation, we still denote this convergent subsequence by
for each i. Since the total space of allocations X is compact, any non-degenerate infinite sequence in X contains a non-degenerate convergent subsequence. By an abuse of notation, we still denote this convergent subsequence by 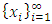 Denote the limit point of this convergent subsequence by
Denote the limit point of this convergent subsequence by 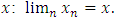 Since
Since 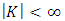 , elements in the core can be discarded from a non-degenerate infinite set of allocations. Thus we can assume
, elements in the core can be discarded from a non-degenerate infinite set of allocations. Thus we can assume 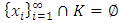 . We can filter this convergent subsequence further to give a non-degenerate subsequence monotone in each of the n coordinate indices
. We can filter this convergent subsequence further to give a non-degenerate subsequence monotone in each of the n coordinate indices 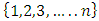 using a geometric filter as follows. In this context, monotonicity means for each of the index
using a geometric filter as follows. In this context, monotonicity means for each of the index 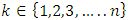 , the sequence of real numbers
, the sequence of real numbers 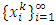 is either an increasing sequence of real numbers, or a decreasing sequence of real numbers, or a constant non-changing sequence consisting of a single real number. To apply the geometric filter, notice that for an arbitrary non-degenerate sequence of real numbers
is either an increasing sequence of real numbers, or a decreasing sequence of real numbers, or a constant non-changing sequence consisting of a single real number. To apply the geometric filter, notice that for an arbitrary non-degenerate sequence of real numbers 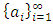 in
in 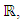 there is a monotone convergent subsequence. Thus for the convergent non-degenerate subsequence of allocations
there is a monotone convergent subsequence. Thus for the convergent non-degenerate subsequence of allocations 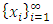 in
in 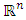 , we can find a monotone subsequence of
, we can find a monotone subsequence of 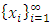 by passing to a monotone subsequence of real numbers in each one of the n coordinate indices starting with the first one. For example, if we denote the sequence of real numbers formed by the kth coordinate of all the allocations in the convergent sequence of allocations in its full multi-index expansion notation by
by passing to a monotone subsequence of real numbers in each one of the n coordinate indices starting with the first one. For example, if we denote the sequence of real numbers formed by the kth coordinate of all the allocations in the convergent sequence of allocations in its full multi-index expansion notation by 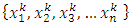 , then we can find a strictly monotone subsequence for this sequence of real numbers. We form a new convergent subsequence in the original convergent sequence of allocations
, then we can find a strictly monotone subsequence for this sequence of real numbers. We form a new convergent subsequence in the original convergent sequence of allocations 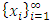 in
in 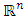 by including only those allocations for which the monotone subsequence is positioned. So for example, if every fourth element in the sequence of real numbers
by including only those allocations for which the monotone subsequence is positioned. So for example, if every fourth element in the sequence of real numbers 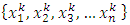 is discarded by this geometric filter, then every corresponding fourth element in the original sequence of convergent allocations
is discarded by this geometric filter, then every corresponding fourth element in the original sequence of convergent allocations 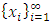 in
in 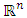 is discarded. An example of the geometric filter is given below. Example: consider the following non-degenerate infinite sequence of allocations in a 1-good 3-player pillage game:
is discarded. An example of the geometric filter is given below. Example: consider the following non-degenerate infinite sequence of allocations in a 1-good 3-player pillage game: 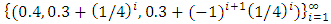 If we pass the sequence formed by the second coordinate through the geometric filter, then a monotone increasing convergent subsequence is achieved by selecting all the even terms
If we pass the sequence formed by the second coordinate through the geometric filter, then a monotone increasing convergent subsequence is achieved by selecting all the even terms 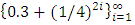 . The reader is cautioned that in doing so, not only are the odd terms in the sequence of real numbers formed by the second coordinate discarded, odd terms in the allocations are also discarded. Therefore, the geometric filter gives the following convergent subsequence, monotone in each of the three indices:
. The reader is cautioned that in doing so, not only are the odd terms in the sequence of real numbers formed by the second coordinate discarded, odd terms in the allocations are also discarded. Therefore, the geometric filter gives the following convergent subsequence, monotone in each of the three indices: 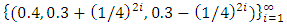 The reader is further cautioned that in the above example the second coordinate and the third coordinate are algebraically coupled. It is possible that in the original sequence of allocations
The reader is further cautioned that in the above example the second coordinate and the third coordinate are algebraically coupled. It is possible that in the original sequence of allocations 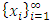 , one or more coordinates is already degenerate before we apply the geometric filter. That is, for a particular index k with
, one or more coordinates is already degenerate before we apply the geometric filter. That is, for a particular index k with 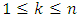 , the sequence
, the sequence 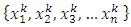 consists of only finitely many real numbers. In that case, we choose one real number for this index and retain all the terms in which this real number appears. Since the original sequence of allocations is non-degenerate, there is at least one index where the sequence of real numbers must consist of infinitely many non-equal real numbers. We start with the first index
consists of only finitely many real numbers. In that case, we choose one real number for this index and retain all the terms in which this real number appears. Since the original sequence of allocations is non-degenerate, there is at least one index where the sequence of real numbers must consist of infinitely many non-equal real numbers. We start with the first index 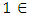
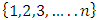 and repeat the process up to the nth index. Since there are only finitely many indices, the geometric filter will result in a convergent non-degenerate sequence monotone in each of the n indices. Due to numerous upper indices, lower indices, and the many filters, we still denote the resulting sequence of allocations as
and repeat the process up to the nth index. Since there are only finitely many indices, the geometric filter will result in a convergent non-degenerate sequence monotone in each of the n indices. Due to numerous upper indices, lower indices, and the many filters, we still denote the resulting sequence of allocations as 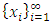 . Notice the filtered sequence has the property that in each coordinate
. Notice the filtered sequence has the property that in each coordinate 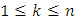 , each one of the following conditions holds:
, each one of the following conditions holds: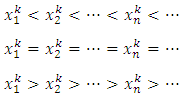 With this filtered sequence, we now consider a forward dominant structure where the more dominant allocations are the ones with higher indices:
With this filtered sequence, we now consider a forward dominant structure where the more dominant allocations are the ones with higher indices: 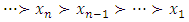 | (7) |
Forward dominance relations have appeared in previous studies of stable sets. For example, McKenzie, Kerber, and Rowat constructed a non-transitive forward dominance loop in a 1-good 4-player pillage game 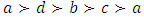 to show the non-uniqueness of stable sets [2]. Each of the above four elements is an “exceptional allocation” in the set
to show the non-uniqueness of stable sets [2]. Each of the above four elements is an “exceptional allocation” in the set 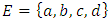 that dominates all other allocations in
that dominates all other allocations in 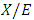 except for the elements in the core K. In their example, the power function has the special numerical property that it uses two different sets of double linear weights with the sum of 1, placed at three different coordinates to equalize the valuations for a and b and likewise for c and d. With these numerical constraints satisfied, the stable sets in this 1-good 4-player pillage game are
except for the elements in the core K. In their example, the power function has the special numerical property that it uses two different sets of double linear weights with the sum of 1, placed at three different coordinates to equalize the valuations for a and b and likewise for c and d. With these numerical constraints satisfied, the stable sets in this 1-good 4-player pillage game are 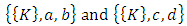 Hence a non-transitive forward dominance structure is carefully constructed using numerical analysis. This construction reveals certain intricate complexities that the simple order axioms set forth in the definition of pillage games allow. As such, special numerical analytic constructions can be achieved to allow for these “exotic” features of pillage games satisfying a set of rational and minimal expectations similar to the philosophical impasse in Arrow’s impossibility theorem. In contrast, our approach is a classic algebra-geometric approach where analytic concepts such as compactness and bounded convergence are used to derive the existence of sequences of allocations with special properties. Recall that the current convergent sequence of allocations is monotone in each of the n indices. With the above forward dominance structure, we haveLemma 1. There exists a subsequence of
Hence a non-transitive forward dominance structure is carefully constructed using numerical analysis. This construction reveals certain intricate complexities that the simple order axioms set forth in the definition of pillage games allow. As such, special numerical analytic constructions can be achieved to allow for these “exotic” features of pillage games satisfying a set of rational and minimal expectations similar to the philosophical impasse in Arrow’s impossibility theorem. In contrast, our approach is a classic algebra-geometric approach where analytic concepts such as compactness and bounded convergence are used to derive the existence of sequences of allocations with special properties. Recall that the current convergent sequence of allocations is monotone in each of the n indices. With the above forward dominance structure, we haveLemma 1. There exists a subsequence of 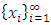 in the above setup such that for any subset C of
in the above setup such that for any subset C of 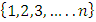 , only one of the following three mutually exclusive relations holds:
, only one of the following three mutually exclusive relations holds: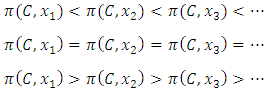 Proof. Since
Proof. Since 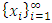 is strictly monotone in each index, if A is a subset of
is strictly monotone in each index, if A is a subset of 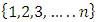 where the
where the 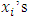 are increasing in their indices
are increasing in their indices 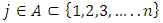 , then by the SR axiom, we have
, then by the SR axiom, we have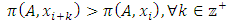 | (8) |
Conversely, if B is a subset of 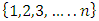 where the
where the 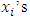 are decreasing in their indices
are decreasing in their indices 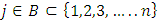 , then by the SR axiom, we have
, then by the SR axiom, we have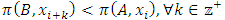 | (9) |
If C is a subset of 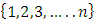 where the
where the 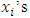 contain both increasing and decreasing indices, we use a unidirectionality filter to achieve monotonicity in
contain both increasing and decreasing indices, we use a unidirectionality filter to achieve monotonicity in 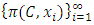 as follows. As a sequence of real numbers,
as follows. As a sequence of real numbers, 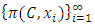 either consists of an infinitely many real numbers or it consists of only finitely many real numbers. If it is infinite, then
either consists of an infinitely many real numbers or it consists of only finitely many real numbers. If it is infinite, then 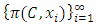 either contains a non-degenerate monotone increasing subsequence or a non-degenerate monotone decreasing subsequence. Assume without the loss of generality that
either contains a non-degenerate monotone increasing subsequence or a non-degenerate monotone decreasing subsequence. Assume without the loss of generality that 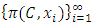 contains a monotone increasing subsequence. Then a new subsequence can be achieved by discarding the terms in
contains a monotone increasing subsequence. Then a new subsequence can be achieved by discarding the terms in 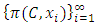 with indices j where the jth term in
with indices j where the jth term in 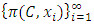 is not monotone increasing. We are then left with a non-degenerate subsequence of allocations
is not monotone increasing. We are then left with a non-degenerate subsequence of allocations 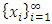 where for the subset
where for the subset 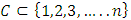 , the sequence of real numbers
, the sequence of real numbers 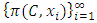 is a monotone increasing sequence. We still denote the newly filtered subsequence of allocations by
is a monotone increasing sequence. We still denote the newly filtered subsequence of allocations by 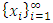 .If the sequence of real numbers
.If the sequence of real numbers 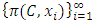 is a finite set, then we take the one of the valuations assumed by the power function restricted to the subset C. Notice because the geometrically filtered allocation sequence
is a finite set, then we take the one of the valuations assumed by the power function restricted to the subset C. Notice because the geometrically filtered allocation sequence 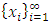 is monotone in each of the n indices, the first case where
is monotone in each of the n indices, the first case where 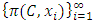 is an infinite set will occur by the SR axiom. Since there are only finitely many subsets of
is an infinite set will occur by the SR axiom. Since there are only finitely many subsets of 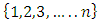 , after finitely many filtering steps, we arrive at a non-degenerate sequence of allocations, monotone in each index with the property that for each subset C of
, after finitely many filtering steps, we arrive at a non-degenerate sequence of allocations, monotone in each index with the property that for each subset C of 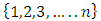 ,
, 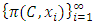 is a monotone sequence of real numbers. This completes the proof. The unidirectionality filter establishes a uniformity in the valuation by the power function with respect to any subset of
is a monotone sequence of real numbers. This completes the proof. The unidirectionality filter establishes a uniformity in the valuation by the power function with respect to any subset of 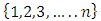 . We now consider the comparison of valuations by the power function with respect to any pair of non-empty and disjoint subsets of
. We now consider the comparison of valuations by the power function with respect to any pair of non-empty and disjoint subsets of 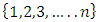 . For any pair of disjoint and non-empty sets
. For any pair of disjoint and non-empty sets 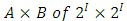 with
with 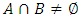 , we examine the sequence of equalities and inequalities that exists between
, we examine the sequence of equalities and inequalities that exists between 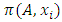 and
and 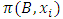 for the filtered allocation sequence
for the filtered allocation sequence 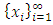 . We haveLemma 2. There exists a subsequence of
. We haveLemma 2. There exists a subsequence of 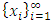 such that for each pair of disjoint and non-empty subsets
such that for each pair of disjoint and non-empty subsets  of
of 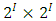 , only one of the following three mutually exclusive relations holds for all allocations in the sequence:
, only one of the following three mutually exclusive relations holds for all allocations in the sequence: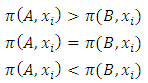 Proof. For each pair of disjoint non-empty subsets
Proof. For each pair of disjoint non-empty subsets 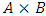 , at least one of the parity relations >, =, or < exists for infinitely many terms. It is certainly possible that two or all three parity relations exist for infinitely many terms in
, at least one of the parity relations >, =, or < exists for infinitely many terms. It is certainly possible that two or all three parity relations exist for infinitely many terms in 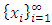 for a particular pair
for a particular pair 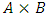 . We select a further subsequence of
. We select a further subsequence of 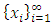 by the following parity comparison filter. If only one of the three above parity relations exists for infinitely many allocations in
by the following parity comparison filter. If only one of the three above parity relations exists for infinitely many allocations in 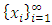 , then there are at most only finitely many allocations in the sequence where the other two parity relations exist. In this case, we filter
, then there are at most only finitely many allocations in the sequence where the other two parity relations exist. In this case, we filter 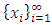 by discarding the finitely many terms for which the other two parity relations hold. For example, if for the pair
by discarding the finitely many terms for which the other two parity relations hold. For example, if for the pair 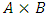 , all but finitely many terms in
, all but finitely many terms in  have
have 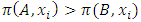 , then we discard the finitely terms where
, then we discard the finitely terms where 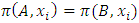 and
and 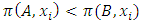 . If two or more of the above parity relations exist for infinitely many allocations in
. If two or more of the above parity relations exist for infinitely many allocations in 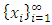 , then we select precisely one relation and discard the other allocations for which the chosen relation does not hold. Since there are only finitely many proper subsets of
, then we select precisely one relation and discard the other allocations for which the chosen relation does not hold. Since there are only finitely many proper subsets of 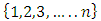 , there are only finitely many disjoint non-empty pairs of
, there are only finitely many disjoint non-empty pairs of 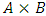 . Therefore the parity comparison filter will stop after all finitely many such pairs
. Therefore the parity comparison filter will stop after all finitely many such pairs 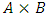 have been filtered, each resulting in an infinite non-degenerate subsequence of allocations. For the convenience of notations, we still denote the final filtered sequence of allocations as
have been filtered, each resulting in an infinite non-degenerate subsequence of allocations. For the convenience of notations, we still denote the final filtered sequence of allocations as 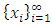 . This completes the proof. Recall that we denoted by x the limit point of the convergent allocation sequence
. This completes the proof. Recall that we denoted by x the limit point of the convergent allocation sequence 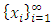 . We now prove a local regularity property of the filtered sequence. Theorem 3. There exists an
. We now prove a local regularity property of the filtered sequence. Theorem 3. There exists an 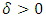 such that in an
such that in an 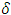 -neighborhood of x, the following equivalence of dominance structure holds:
-neighborhood of x, the following equivalence of dominance structure holds: 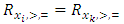 | (10) |
Proof. With the final convergent sequence thus filtered, we have that for every pair of disjoint non-empty subsets 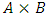 , the entire filtered sequence satisfies the same parity relations: <, =, or >. But these pairs of disjoint non-empty subsets A and B are precisely the pair of subsets that define the dominance relations for each allocation
, the entire filtered sequence satisfies the same parity relations: <, =, or >. But these pairs of disjoint non-empty subsets A and B are precisely the pair of subsets that define the dominance relations for each allocation 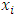 . That is, these pairs are precisely the pairs of subsets that define the win sets and lose sets for
. That is, these pairs are precisely the pairs of subsets that define the win sets and lose sets for 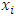 against any other allocation. For example, if
against any other allocation. For example, if 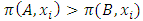 , then we have
, then we have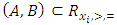 | (11) |
Therefore, if 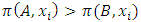 for all indices in the ultrafiltered sequence of allocations
for all indices in the ultrafiltered sequence of allocations 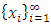 for each pair of disjoint non-empty subsets, then we have
for each pair of disjoint non-empty subsets, then we have 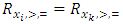 Notice the above equality relation may not hold true if we only have a convergent sequence of allocations approaching x. The three filters added a further rigidity to the original sequence of allocations such that in the end with the ultra-filtered sequence, these desired geometric and parity comparison properties hold. This completes the proof.We now summarize the three different filters from the above discussions in their prescribed order into an algorithm. The reader is reminded that because of the limit of mathematical notations, we still denote the filtered sequence by
Notice the above equality relation may not hold true if we only have a convergent sequence of allocations approaching x. The three filters added a further rigidity to the original sequence of allocations such that in the end with the ultra-filtered sequence, these desired geometric and parity comparison properties hold. This completes the proof.We now summarize the three different filters from the above discussions in their prescribed order into an algorithm. The reader is reminded that because of the limit of mathematical notations, we still denote the filtered sequence by 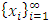 after each of the three filters. Given an infinite set of allocations
after each of the three filters. Given an infinite set of allocations 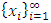 , the first filter is the geometric filter where we pass the original sequence through to achieve a subsequence monotone in each of the n coordinates. The second filter is the unidirectionality filter where for each proper subset
, the first filter is the geometric filter where we pass the original sequence through to achieve a subsequence monotone in each of the n coordinates. The second filter is the unidirectionality filter where for each proper subset 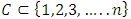 , an increasing, decreasing, or constant infinite subsequence of real numbers in
, an increasing, decreasing, or constant infinite subsequence of real numbers in 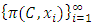 is selected. The third filter is the parity comparison filter where for each pair of disjoint non-empty subsets
is selected. The third filter is the parity comparison filter where for each pair of disjoint non-empty subsets 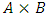 , we select an infinite subsequence in which only one of the three parity relations <, =, or > holds true all allocations in the chosen subsequence. This triple step algorithm gives an infinite sequence of allocations
, we select an infinite subsequence in which only one of the three parity relations <, =, or > holds true all allocations in the chosen subsequence. This triple step algorithm gives an infinite sequence of allocations 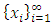 with the desired dominance relation properties. Notice in the forward dominance relation, we did not assume transitivity. That is, we did not assume
with the desired dominance relation properties. Notice in the forward dominance relation, we did not assume transitivity. That is, we did not assume 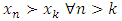 . But we will show that with our filtered sequence of allocations satisfying the geometric, the unidirectionality, and parity comparison relations, the forward dominance structure is in fact transitive. Theorem 4. The filtered sequence of allocations
. But we will show that with our filtered sequence of allocations satisfying the geometric, the unidirectionality, and parity comparison relations, the forward dominance structure is in fact transitive. Theorem 4. The filtered sequence of allocations 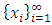 is transitively dominant:
is transitively dominant: 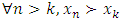 .Proof. Since
.Proof. Since 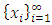 is strictly monotone in each coordinate, if i is an index where
is strictly monotone in each coordinate, if i is an index where 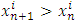 , then
, then 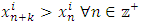 . Then by monotonicity, if
. Then by monotonicity, if 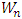 is the win set for
is the win set for 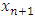 over
over 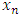 and
and 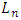 is the lose set for
is the lose set for 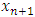 over
over 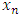 , then
, then 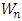 is also the win set for
is also the win set for 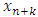 over
over 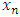 and
and 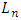 is also the lose set for
is also the lose set for 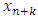 over
over 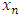 . Therefore we have
. Therefore we have 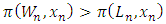 when
when 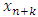 is compared to
is compared to 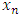 . But this is
. But this is 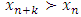 . This completes the proof.
. This completes the proof.
5. The Theoretical Model
In the previous sections, we started with a highly redundant infinite sequence of allocations 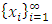 . Then different filters were used to reduce these allocations in order to achieve a convergent sequence with desired properties. In this section, we put these results together and examine a theoretical model that satisfies a set of conditions necessary for the existence of an infinite set of stable set.Since any stable set must have finite cardinality, the challenge in finding a model that makes an infinite set of stable sets possible is closing the dominance loop for any non-core allocations in a given allocation set
. Then different filters were used to reduce these allocations in order to achieve a convergent sequence with desired properties. In this section, we put these results together and examine a theoretical model that satisfies a set of conditions necessary for the existence of an infinite set of stable set.Since any stable set must have finite cardinality, the challenge in finding a model that makes an infinite set of stable sets possible is closing the dominance loop for any non-core allocations in a given allocation set 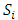 against the non-core allocations in another set
against the non-core allocations in another set 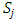 for a countably infinite family of such sets. This implies when comparing two distinct allocation sets
for a countably infinite family of such sets. This implies when comparing two distinct allocation sets 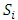 and
and 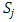 , any chain of dominance starting with a non-core allocation in
, any chain of dominance starting with a non-core allocation in 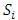 must end after finitely many allocations with a non-core allocation in the same set
must end after finitely many allocations with a non-core allocation in the same set 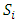 in order for
in order for 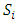 to satisfy external stability against
to satisfy external stability against 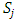 :
: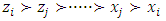 with
with 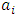 and
and 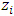 in
in 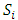 and
and 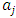 and
and 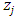 in
in 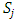 . Since this relation must also hold true for
. Since this relation must also hold true for 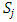 against
against 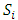 , a necessary condition is the existence of two distinct sets of allocations. Since this second set of allocations consists of non-core elements, dominance structures also exist within these allocations. Let
, a necessary condition is the existence of two distinct sets of allocations. Since this second set of allocations consists of non-core elements, dominance structures also exist within these allocations. Let 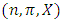 be a continuous pillage game with a non-empty core K. Suppose we have an infinite sequence of forward dominant allocations
be a continuous pillage game with a non-empty core K. Suppose we have an infinite sequence of forward dominant allocations 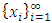 satisfying the monotonicity, unidirectionality, and parity comparison conditions in section 4. This implies that two distinct allocations
satisfying the monotonicity, unidirectionality, and parity comparison conditions in section 4. This implies that two distinct allocations 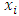 and
and 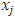 can belong to two distinct sets
can belong to two distinct sets 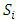 and
and 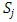 to satisfy internal stability. Let K and
to satisfy internal stability. Let K and 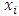 be in
be in 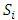 . By theorem 4,
. By theorem 4, 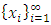 is transitively dominant. External stability necessitates allocations
is transitively dominant. External stability necessitates allocations 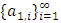 that dominate
that dominate 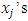 down the chain by theorem 2. In the notation
down the chain by theorem 2. In the notation 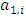 , the first right index 1 indicates that this sequence of allocations
, the first right index 1 indicates that this sequence of allocations 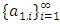 is the first sequence needed after the original sequence
is the first sequence needed after the original sequence 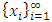 . The second right index i indicates the position of the element
. The second right index i indicates the position of the element 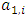 in the set of allocations. Namely,
in the set of allocations. Namely, 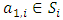 . Thus we have for
. Thus we have for 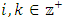
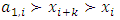 Lemma 3.
Lemma 3. 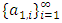 is a sequence of pairwise distinct allocations. That is,
is a sequence of pairwise distinct allocations. That is, 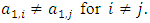 Proof. Suppose for
Proof. Suppose for 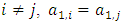 . Assume without the loss of generality that
. Assume without the loss of generality that 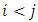 . Since
. Since 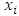 and
and 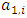 are in
are in 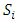 and
and 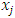 and
and 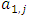 are in
are in 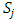 , forward dominance of
, forward dominance of 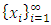 implies that we have
implies that we have 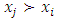 By external stability of
By external stability of 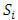 , we also have
, we also have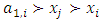 Since
Since 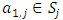 , if
, if 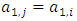 , the dominance sequence above implies that
, the dominance sequence above implies that 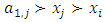 But this contradicts the internal stability of
But this contradicts the internal stability of 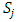 . Thus we must have
. Thus we must have 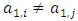 for
for 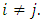 This completes the proof. The above lemma implies that an infinite sequence of allocations
This completes the proof. The above lemma implies that an infinite sequence of allocations 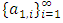 where
where 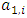 dominates an infinite subset of
dominates an infinite subset of 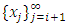 is needed to ensure external stability. Thus we have that K,
is needed to ensure external stability. Thus we have that K, 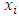 and
and 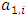 now belong to
now belong to 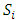 . Since we have
. Since we have 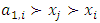 and
and 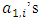 are non-core allocations, there is an allocation in
are non-core allocations, there is an allocation in 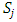 that dominates
that dominates 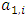 . This necessitates the existence of a second sequence of allocations
. This necessitates the existence of a second sequence of allocations 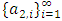 with
with 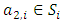 . We now consider a set of conditions sufficient for the existence of an
. We now consider a set of conditions sufficient for the existence of an 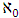 -order set of stable sets in a continuous pillage game: 1.
-order set of stable sets in a continuous pillage game: 1. 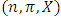 contains pairwise distinct forward dominant sequences
contains pairwise distinct forward dominant sequences 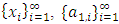 , and
, and 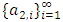 in the interior of X such that each sequence satisfies the conditions of monotonicity, unidirectionality, and parity comparison. 2. There exists a finite set of non-core allocations
in the interior of X such that each sequence satisfies the conditions of monotonicity, unidirectionality, and parity comparison. 2. There exists a finite set of non-core allocations 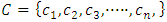 with
with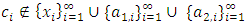 ;
; 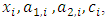 and elements in K do not dominate each other; and
and elements in K do not dominate each other; and 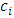 does not dominate
does not dominate 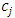 for
for 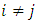 .3.
.3. 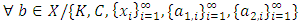 , b is either dominated by a subset of the core, or by allocations in C, or by an allocation in
, b is either dominated by a subset of the core, or by allocations in C, or by an allocation in 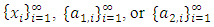 for each i. 4. The following inter-sequence dominance structure holds
for each i. 4. The following inter-sequence dominance structure holds 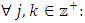
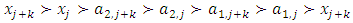 Theorem 6. A continuous pillage game with a power function
Theorem 6. A continuous pillage game with a power function 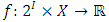 satisfying the three order axioms and conditions (1) through (4) contains an
satisfying the three order axioms and conditions (1) through (4) contains an 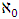 -order of stable sets
-order of stable sets 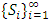 with
with 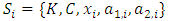 .Proof. Let
.Proof. Let 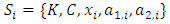 . Condition (1) gives the infinite sequences where valuation comparisons can be made by the power function. These sequences satisfy the conditions of monotonicity, unidirectionality, and parity comparison. Forward dominant means that
. Condition (1) gives the infinite sequences where valuation comparisons can be made by the power function. These sequences satisfy the conditions of monotonicity, unidirectionality, and parity comparison. Forward dominant means that 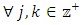 , we have the following relations:
, we have the following relations: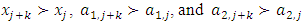 | (12) |
Conditions (1) and (4) taken together give the closed loop of finite length as follows. 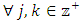 , any non-core allocation in
, any non-core allocation in 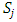 gives a unique chain of dominance that ends also in
gives a unique chain of dominance that ends also in 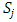 . For
. For 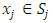 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: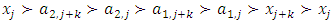 | (13) |
For 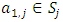 , conditions (1) and (4) also give the following finite chain of dominance:
, conditions (1) and (4) also give the following finite chain of dominance: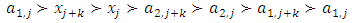 | (14) |
Similarly for 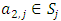 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: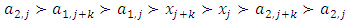 | (15) |
Therefore when comparing 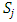 with
with 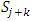 , if we start with any non-core allocation in
, if we start with any non-core allocation in 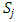 , the chain of dominance structure is always a cyclic loop of finite length that ends in a non-core allocation in
, the chain of dominance structure is always a cyclic loop of finite length that ends in a non-core allocation in 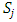 to ensure external stability. Starting with any non-core allocation in
to ensure external stability. Starting with any non-core allocation in 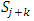 , conditions (1) and (4) also give a chain of finite length against non-core allocations in
, conditions (1) and (4) also give a chain of finite length against non-core allocations in 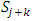 . For
. For 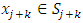 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: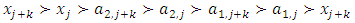 | (16) |
For 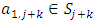 , conditions (1) and (4) also give the following finite chain of dominance:
, conditions (1) and (4) also give the following finite chain of dominance: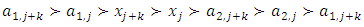 | (17) |
And similarly for 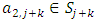 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: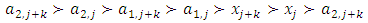 | (18) |
Thus, when comparing the non-core allocations in two stable sets 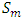 and
and 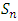 , starting with any non-core allocation in the first stable set
, starting with any non-core allocation in the first stable set 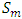 , a dominance loop of finite length ending also with an allocation in
, a dominance loop of finite length ending also with an allocation in 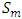 exists both for
exists both for 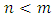 and
and 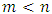 . Condition (2) gives internal stability in that for any pair of allocations a and b in
. Condition (2) gives internal stability in that for any pair of allocations a and b in 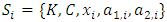 , if we denote
, if we denote 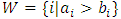 and
and 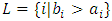 , then we have
, then we have 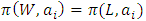 and
and 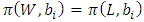 . Condition (3) gives external stability for
. Condition (3) gives external stability for 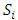 . The reader is cautioned that the theorem only gives a special set of sufficient conditions – these conditions may not be necessary. Indeed there can be numerous examples of pillage games in which conditions other than conditions (1) through (4) are satisfied but still have infinitely many stable sets.
. The reader is cautioned that the theorem only gives a special set of sufficient conditions – these conditions may not be necessary. Indeed there can be numerous examples of pillage games in which conditions other than conditions (1) through (4) are satisfied but still have infinitely many stable sets.
6. Conclusions
Continuity gives many advantages in analysing pillage games. For example, since 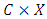 is a compact set for any
is a compact set for any 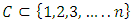 , its image
, its image 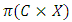 is also a compact set in
is also a compact set in 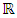 . Hence
. Hence 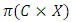 is a bounded set. In addition, since a continuous function on a compact set is also uniformly continuous,
is a bounded set. In addition, since a continuous function on a compact set is also uniformly continuous, 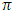 is uniformly continuous on
is uniformly continuous on 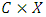 . These rich structural properties lead to a simpler path of analysis of continuous pillage games. We now propose two possible future approaches to the study of pillage games, one for the continuous case and the other for the general case without the assumption of continuity. If a pillage game is continuous, the boundedness property and the subsequent uniform continuity property stated above allow for a profile of
. These rich structural properties lead to a simpler path of analysis of continuous pillage games. We now propose two possible future approaches to the study of pillage games, one for the continuous case and the other for the general case without the assumption of continuity. If a pillage game is continuous, the boundedness property and the subsequent uniform continuity property stated above allow for a profile of 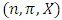 to be constructed as follows. Given any
to be constructed as follows. Given any 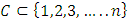 and
and 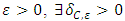 depending on
depending on 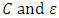 such that
such that 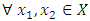 with
with 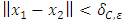 , we have
, we have 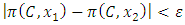 . Since there are only finitely many subsets of
. Since there are only finitely many subsets of 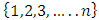 , a lower bound on all of the
, a lower bound on all of the 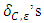 with C spanning
with C spanning 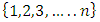 can be found. As a result, the power function’s growth rate can be controlled. Thus starting at any allocation x, one can ask: what is the maximum rate a coalition C’s collective power can grow by moving to a nearby allocation x’. In the general case without the assumption of continuity, notice that pillage games have certain measure-theoretic properties that give insights and characterize classes of games beyond pillage games. Given an allocation x, the WC condition introduces a property similar to that of a measure
can be found. As a result, the power function’s growth rate can be controlled. Thus starting at any allocation x, one can ask: what is the maximum rate a coalition C’s collective power can grow by moving to a nearby allocation x’. In the general case without the assumption of continuity, notice that pillage games have certain measure-theoretic properties that give insights and characterize classes of games beyond pillage games. Given an allocation x, the WC condition introduces a property similar to that of a measure 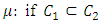 , then
, then 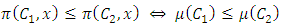 | (19) |
Thus for suitable subsets of 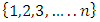 , a binary relation with respect to set inclusion exists. One needs to use caution in that if
, a binary relation with respect to set inclusion exists. One needs to use caution in that if 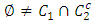 and
and 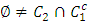 , no conclusion can be made on the comparison of
, no conclusion can be made on the comparison of 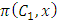 and
and 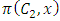 . One can obtain certain quantitative comparisons because the following set inclusion holds:
. One can obtain certain quantitative comparisons because the following set inclusion holds: 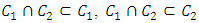 , and
, and 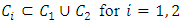 .From the other end, given
.From the other end, given 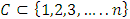 . the WR and SR conditions also impose a poset structure
. the WR and SR conditions also impose a poset structure 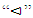 on allocations in X as follows. If
on allocations in X as follows. If 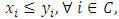 then
then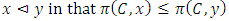 | (20) |
Without additional restrictions on 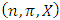 , one cannot compare
, one cannot compare 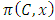 to
to 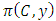 if
if 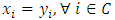 . But these above stated properties indeed make
. But these above stated properties indeed make 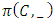 a “semi-poset”
a “semi-poset”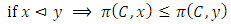 | (21) |
In a certain sense, 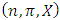 displays properties of a fibre bundle. That is,
displays properties of a fibre bundle. That is, 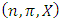 can be considered as a map on the cross product
can be considered as a map on the cross product 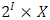 that fibers over the subsets of
that fibers over the subsets of 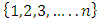 . Given a subset
. Given a subset 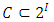 , the fibering respects set inclusions. Conversely, when restricted to a particular subset, the fibre splitting respects the poset structure stated above. Given these observations, the following question can be asked: is there a general form of representation theorem for pillage games? In other words, can there exist a real-valued function
, the fibering respects set inclusions. Conversely, when restricted to a particular subset, the fibre splitting respects the poset structure stated above. Given these observations, the following question can be asked: is there a general form of representation theorem for pillage games? In other words, can there exist a real-valued function 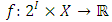 and a semi-measure
and a semi-measure 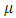 such that given
such that given 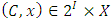 , we have
, we have 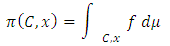 | (22) |
It is understood that integrability in this case can be made more general than that of Riemann integration or even Lebesgue integrability. We should be advised that if a semi-measure 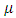 exists on
exists on 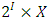 such that the power function
such that the power function 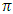 can be represented as the integral of this
can be represented as the integral of this  -measurable real-valued function f, the integral of f could be unbounded over the product space
-measurable real-valued function f, the integral of f could be unbounded over the product space 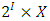 :
: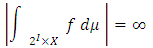 | (23) |
If this representation is tenable even in the greatest generality, it can, for pillage games and for other cooperative games, reduce the study of these games essentially to the properties of the representation function f and the semi-measure 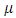 .
.
ACKNOWLEDGEMENTS
I thank the Editor and the two anonymous referees for their helpful suggestions. I thank Dr. Yu Chen for her encouragement during the writing of this paper.I also thank Dr. Brad Engle for his kind support during the revision of this paper.
References
| [1] | J. Jordan, “Pillage and Property,” Journal of Economic Theory, vol. (131), pp. 26-44, 2006. |
| [2] | S. McKenzie, M. Kerber, and C. Rowat, “Pillage Games with Multiple Stable Sets,” International Journal of Game Theory, vol. (44), pp. 993-1013, 2016. |
| [3] | D. Saxton, “Strictly Monotonic Multidimensional Sequences and Stable Sets in Pillage Games,” Journal of Combinatorial Theory, vol. (118), pp. 510-524, 2011. |
| [4] | A. Beardon, and C. Rowat, “Efficient Sets Are Small,” Journal of Mathematical Economics, vol. (4), pp. 367-374, 2013. |
| [5] | L. Shapley, “Contribution to the Theory of Games”, Princeton University Press, New Jersey, (1959). |



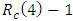 where
where 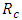 is the diagonal multicolor Ramsey number and c is the number of players in the game [2]. Examining strictly monotonic sequences in dimensions greater than 1, Saxton showed that
is the diagonal multicolor Ramsey number and c is the number of players in the game [2]. Examining strictly monotonic sequences in dimensions greater than 1, Saxton showed that  , the cardinality of a stable set in an n-player pillage game satisfies
, the cardinality of a stable set in an n-player pillage game satisfies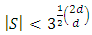
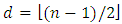 is the floor function [3]. Using measure theory, Beardon and Rowat was able to represent any internally stable set as a finite union of sets satisfying certain pairwise comparison conditions, thereby proving that a stable set's topological dimension in an n-player, m-good pillage game is bounded above by
is the floor function [3]. Using measure theory, Beardon and Rowat was able to represent any internally stable set as a finite union of sets satisfying certain pairwise comparison conditions, thereby proving that a stable set's topological dimension in an n-player, m-good pillage game is bounded above by 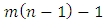 [4].These properties on stable sets prompted the question: can there be a pillage game with infinitely many stable sets, namely is there a pillage game where the collection of stable set is of order
[4].These properties on stable sets prompted the question: can there be a pillage game with infinitely many stable sets, namely is there a pillage game where the collection of stable set is of order 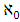 or greater? This question is significant in cooperative games. Historically, Shapley found examples of cooperative games that have infinitely many stable sets by using characteristic functions [5]. In pillage games, McKenzie, Kerber, and Rowat constructed an example of a pillage game with multiple independent stable sets [2]. Thus the above question deserves some serious consideration. In this paper, we give a partial answer to this question. We consider the case of a single good continuous pillage game with non-empty core under a forward dominance structure. We examine a theoretical model of a continuous pillage game satisfying the forward dominance condition. The creation of a concrete model depends on a function satisfying the numerical constraints that permits these conditions. Examples will be given in this paper, we defer the task of finding a concrete example satisfying the many numerical properties set forth in his paper since such a concrete example requires the careful coding by a computer language specialist who encodes these properties in an algorithm and tests it on a work station with sufficient computing power to effect such concrete examples. As such, the primary contribution of this paper is theoretical. The format of this paper is as follows: section 2 of the paper gives the basic background of pillage games. Section 3 introduces a basic property of continuous pillage games - a rigidity theorem. This theorem gives the local structure of dominance in an infinite sequence of allocations as it approaches its limit point. In section 4, using the rigidity theorem, we establish a weak convergence theorem on the dominance structure of any sequence of allocations by using ultrafilters that select subsequences based on geometric properties, unidirectionality conditions, and parity comparison conditions. In section 5, we combine the above results to show a theoretical model in which a set of sufficient conditions for an infinite set of stable sets exists under a cyclic forward dominance structure.In the discussions of section 6, we provide a possible future approach to the study of pillage games and indeed cooperative games in general by highlighting certain fibre bundle properties embedded in pillage games and the possibility of a representation theorem for power functions. The fibre bundle properties are a signature property satisfied by pillage games without the requirement of continuity. Fibre bundles considerations are connected to measure-theoretic integrations in the broader sense. Integration over the base in a fibre bundle points to a representation theorem for pillage games similar to the Riesz representation theorem in classical functional analysis. As a result, fundamental questions in these games such as dominance, stability, and power dynamics among coalitions can be examined through questions about their respective fibre-theoretic analogues such as minimax plateau studies, fibre neighbourhood investigations, and local-global duality studies on function spaces over the fibre bases.
or greater? This question is significant in cooperative games. Historically, Shapley found examples of cooperative games that have infinitely many stable sets by using characteristic functions [5]. In pillage games, McKenzie, Kerber, and Rowat constructed an example of a pillage game with multiple independent stable sets [2]. Thus the above question deserves some serious consideration. In this paper, we give a partial answer to this question. We consider the case of a single good continuous pillage game with non-empty core under a forward dominance structure. We examine a theoretical model of a continuous pillage game satisfying the forward dominance condition. The creation of a concrete model depends on a function satisfying the numerical constraints that permits these conditions. Examples will be given in this paper, we defer the task of finding a concrete example satisfying the many numerical properties set forth in his paper since such a concrete example requires the careful coding by a computer language specialist who encodes these properties in an algorithm and tests it on a work station with sufficient computing power to effect such concrete examples. As such, the primary contribution of this paper is theoretical. The format of this paper is as follows: section 2 of the paper gives the basic background of pillage games. Section 3 introduces a basic property of continuous pillage games - a rigidity theorem. This theorem gives the local structure of dominance in an infinite sequence of allocations as it approaches its limit point. In section 4, using the rigidity theorem, we establish a weak convergence theorem on the dominance structure of any sequence of allocations by using ultrafilters that select subsequences based on geometric properties, unidirectionality conditions, and parity comparison conditions. In section 5, we combine the above results to show a theoretical model in which a set of sufficient conditions for an infinite set of stable sets exists under a cyclic forward dominance structure.In the discussions of section 6, we provide a possible future approach to the study of pillage games and indeed cooperative games in general by highlighting certain fibre bundle properties embedded in pillage games and the possibility of a representation theorem for power functions. The fibre bundle properties are a signature property satisfied by pillage games without the requirement of continuity. Fibre bundles considerations are connected to measure-theoretic integrations in the broader sense. Integration over the base in a fibre bundle points to a representation theorem for pillage games similar to the Riesz representation theorem in classical functional analysis. As a result, fundamental questions in these games such as dominance, stability, and power dynamics among coalitions can be examined through questions about their respective fibre-theoretic analogues such as minimax plateau studies, fibre neighbourhood investigations, and local-global duality studies on function spaces over the fibre bases.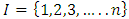 dividing a single good/commodity where the players' shares of the good are represented as vectors in the convex hull X with vertex at unity on each of the n axes in
dividing a single good/commodity where the players' shares of the good are represented as vectors in the convex hull X with vertex at unity on each of the n axes in 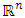 :
: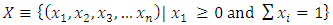
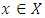 is called an allocation of the good. Given an allocation x, its utility with respect to a subset of players
is called an allocation of the good. Given an allocation x, its utility with respect to a subset of players 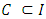 is measured by a real-valued function called the power function
is measured by a real-valued function called the power function 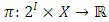 satisfying the three order axioms:
satisfying the three order axioms: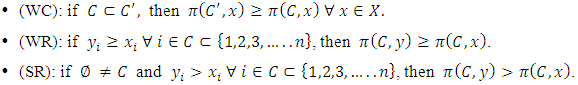 The notation
The notation 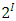 denotes the power set of the n players. Thus a pillage game is a triple
denotes the power set of the n players. Thus a pillage game is a triple 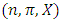 with the above properties. If there is the additional requirement that for each
with the above properties. If there is the additional requirement that for each 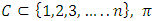 is continuous on the allocation variable x, then we call
is continuous on the allocation variable x, then we call 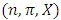 a continuous pillage game.An allocation a dominates another allocation b, denoted as
a continuous pillage game.An allocation a dominates another allocation b, denoted as 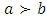 if
if 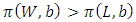 where
where 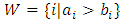 and
and 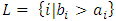 . We call W the win set and L the lose set. The idea of dominance measured by the power function is that given an allocation, a more dominant player can move toward another allocation that confers higher utility. The power function therefore both informs and is informed by the allocation structures. Thus its properties are of critical interest in pillage games.Given
. We call W the win set and L the lose set. The idea of dominance measured by the power function is that given an allocation, a more dominant player can move toward another allocation that confers higher utility. The power function therefore both informs and is informed by the allocation structures. Thus its properties are of critical interest in pillage games.Given 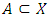 , the dominion of A, denoted as
, the dominion of A, denoted as 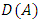 is the set of allocations that are dominated by some element of
is the set of allocations that are dominated by some element of 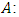
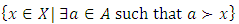 . Thus
. Thus 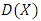 is the set of allocations that are dominated by at least one other allocation. The core, denoted as K, is the set of un-dominated allocations, i.e.
is the set of allocations that are dominated by at least one other allocation. The core, denoted as K, is the set of un-dominated allocations, i.e. 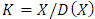 . A set A is said to satisfy internal stability if dominance does not occur between allocations of
. A set A is said to satisfy internal stability if dominance does not occur between allocations of 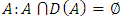 . Clearly the core K is both internally stable and contained in any internally stable set. A is said to satisfy external stability if
. Clearly the core K is both internally stable and contained in any internally stable set. A is said to satisfy external stability if 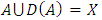 . A set A is called a stable set if it satisfies both internal and external stability. Jordan showed that an internally stable set of a pillage game can contain only finitely many allocations [1].
. A set A is called a stable set if it satisfies both internal and external stability. Jordan showed that an internally stable set of a pillage game can contain only finitely many allocations [1].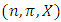 be a continuous pillage game. Let
be a continuous pillage game. Let 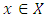 be an allocation. If A and B are two non-empty and non-intersecting subsets of
be an allocation. If A and B are two non-empty and non-intersecting subsets of 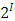 , then the power function can assume any of the following 3 all-inclusive but mutually exclusive relations on A and B at x:
, then the power function can assume any of the following 3 all-inclusive but mutually exclusive relations on A and B at x: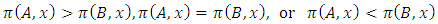 Definition 1. Let x be an allocation in a continuous pillage game
Definition 1. Let x be an allocation in a continuous pillage game 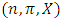 .(1) Let
.(1) Let 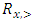 denote the set of all non-empty and non-intersecting pairs of sets
denote the set of all non-empty and non-intersecting pairs of sets 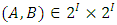 such that
such that 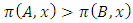 .(2) Similarly, let
.(2) Similarly, let 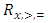 denote the set of all non-empty and non-intersecting pairs of sets
denote the set of all non-empty and non-intersecting pairs of sets 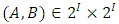 such that
such that 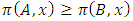 .Theorem 1. Given a continuous pillage game
.Theorem 1. Given a continuous pillage game  , let
, let  such that
such that 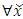 with
with 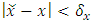 , we have
, we have 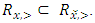 Here
Here 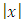 is the Euclidean norm on
is the Euclidean norm on 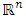 .Proof. We examine the disjoints sets
.Proof. We examine the disjoints sets 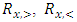 , and
, and 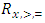 . Let
. Let 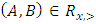 , by definition,
, by definition, 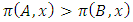 . Denote
. Denote 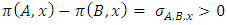 . Notice
. Notice 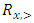 is a finite set because the power set
is a finite set because the power set 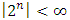 . In fact
. In fact 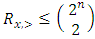
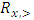 has cardinality m:
has cardinality m: 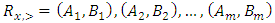 . We also have the corresponding
. We also have the corresponding 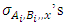 , one for each pair of
, one for each pair of 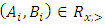 . The continuity of
. The continuity of  means that the power function
means that the power function 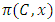 is continuous on the allocation variable x given a fixed set
is continuous on the allocation variable x given a fixed set 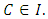 This implies for any
This implies for any 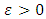 , there is a
, there is a 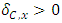 such that
such that 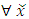 with
with 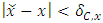 , we have
, we have 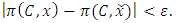 One needs take caution that given an x and an
One needs take caution that given an x and an 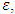 unless uniform continuity is assumed, different subsets of
unless uniform continuity is assumed, different subsets of 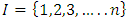 will require different
will require different 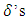 , one for each subset
, one for each subset 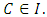 Let
Let 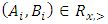 , as before, we have
, as before, we have 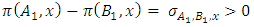 . Thus we have
. Thus we have 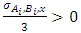
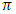 , we choose two neighborhoods: a
, we choose two neighborhoods: a 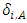 -neighbourhood for the set
-neighbourhood for the set 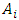 and a
and a 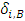 -neighbourhood for the set
-neighbourhood for the set 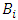 such that
such that 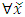 with
with 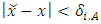 and
and 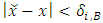 we have
we have 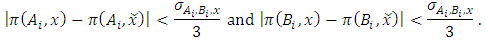 Let
Let 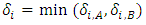 , then for all
, then for all 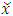 with
with 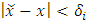 , we have
, we have 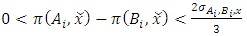
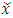 within a small neighborhood of x, if
within a small neighborhood of x, if 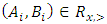 , then
, then 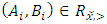 . There are only finitely many pairs of sets
. There are only finitely many pairs of sets 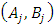 in
in 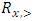 . Each pair
. Each pair 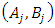 has a corresponding
has a corresponding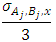 and a corresponding
and a corresponding 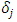 . To extend the above inclusion to all pairs of sets
. To extend the above inclusion to all pairs of sets 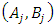 in
in 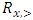 , we define
, we define 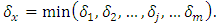 Then for all
Then for all 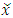 with
with 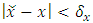 and for all
and for all 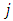 with
with 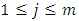 , we have
, we have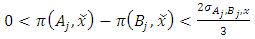
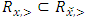 . This completes the proof. This theorem implies that the dominance structure at a point is informed or “bounded” by a larger set of dominance structures of the points in a small neighbourhood near that point. In the next section, we will examine the case of a set of infinitely many allocations under a forward dominance structure. The theorem above will create certain useful properties in a special subset of these allocations.
. This completes the proof. This theorem implies that the dominance structure at a point is informed or “bounded” by a larger set of dominance structures of the points in a small neighbourhood near that point. In the next section, we will examine the case of a set of infinitely many allocations under a forward dominance structure. The theorem above will create certain useful properties in a special subset of these allocations. 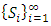 and derive a convergent theorem on the dominance structures. Jordan proved that the cardinality of a stable set in a pillage game is finite [1]. Thus if an infinite set of stable sets is possible in a pillage game with non-empty core K, each stable set must have finite cardinality and each
and derive a convergent theorem on the dominance structures. Jordan proved that the cardinality of a stable set in a pillage game is finite [1]. Thus if an infinite set of stable sets is possible in a pillage game with non-empty core K, each stable set must have finite cardinality and each 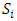 must contain at least one non-core allocation
must contain at least one non-core allocation 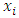 .Since
.Since 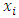 is not in the core, it is dominated by some other allocations. To achieve external stability, each stable set
is not in the core, it is dominated by some other allocations. To achieve external stability, each stable set 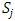 with
with 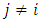 must contain at least one allocation that dominates
must contain at least one allocation that dominates 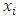 . Conversely,
. Conversely, 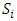 must also contain elements that dominate
must also contain elements that dominate 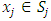 . To maintain internal stability, none of the elements that dominate
. To maintain internal stability, none of the elements that dominate 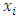 can be in
can be in 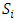 . In particular,
. In particular, 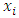 cannot be dominated by any core element. The Jordan finiteness theorem means that each stable set
cannot be dominated by any core element. The Jordan finiteness theorem means that each stable set 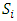 must achieve external stability
must achieve external stability 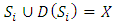 with only finitely many elements. Denote this set of non-core allocations in
with only finitely many elements. Denote this set of non-core allocations in 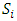 by
by 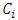 . Together these two conditions imply that if a continuous pillage game with non-empty core has infinitely many stable sets, each stable set
. Together these two conditions imply that if a continuous pillage game with non-empty core has infinitely many stable sets, each stable set 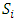 must contain a finite set
must contain a finite set 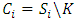 with
with 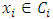 and
and 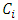 must contain allocations that dominate
must contain allocations that dominate 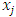 for all
for all 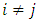 . With the above observations, we prove an immediate property of these pillage games. Theorem 2. If a continuous pillage game
. With the above observations, we prove an immediate property of these pillage games. Theorem 2. If a continuous pillage game 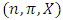 with infinitely many stable sets
with infinitely many stable sets 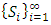 described above exists, then each
described above exists, then each 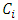 contains at least two allocations.Proof. Given two distinct stable sets
contains at least two allocations.Proof. Given two distinct stable sets 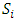 and
and 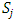 in this setup, to satisfy external stability,
in this setup, to satisfy external stability, 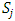 must contain a non-core element in
must contain a non-core element in 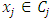 to dominate
to dominate 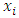 . In turn,
. In turn, 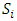 must contain a second element
must contain a second element 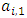 that dominates
that dominates 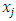 to achieve external stability. Furthermore,
to achieve external stability. Furthermore, 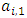 cannot be a core element because
cannot be a core element because 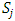 contains the same core K as
contains the same core K as 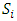 and
and 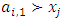 violates internal stability for the stable set
violates internal stability for the stable set 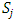 . So there are at least two allocations
. So there are at least two allocations 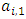 and
and 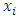 in
in 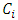 . A symmetric argument shows that
. A symmetric argument shows that 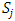 must also contain at least two elements. This completes the proof. Notice since
must also contain at least two elements. This completes the proof. Notice since 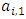 is not in the core, it must also be dominated by some non-core allocations in
is not in the core, it must also be dominated by some non-core allocations in 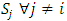 for
for 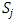 to achieve external stability. Therefore when the non-core elements of
to achieve external stability. Therefore when the non-core elements of 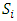 and
and 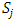 are compared, there is a chain of dominance between these allocations. External stability of each stable set implies that any chain of dominance between allocations from two stable sets, starting with a non-core allocation in
are compared, there is a chain of dominance between these allocations. External stability of each stable set implies that any chain of dominance between allocations from two stable sets, starting with a non-core allocation in 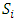 must also end with a non-core allocation in
must also end with a non-core allocation in 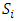 . A symmetric argument shows that this is also true if we start with a non-core allocation in
. A symmetric argument shows that this is also true if we start with a non-core allocation in 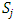 against
against 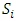 . The finiteness condition along with the above analysis implies a structural necessity for
. The finiteness condition along with the above analysis implies a structural necessity for 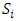 : since card
: since card 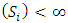 , each non-core allocation in
, each non-core allocation in 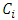 must complete a dominance loop of finite length which also ends with an allocation in
must complete a dominance loop of finite length which also ends with an allocation in 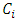 to achieve external stability. Therefore, there is a cyclicity in the dominance structure. This cyclicity allows closure in the sense that a chain starting with a non-core element in one stable set must return upon the same stable set when compared with the non-core elements in anther stable set. Thus a model of pillage game with infinite stable sets must have this cyclic closure property. Once this is achieved, the logical impossibility of a dominance loop never returning to itself is removed. The remaining work is to find a specific function with the numerical characteristics that satisfies the above mentioned cyclic dominance structure conditions. Consider a continuous pillage game
to achieve external stability. Therefore, there is a cyclicity in the dominance structure. This cyclicity allows closure in the sense that a chain starting with a non-core element in one stable set must return upon the same stable set when compared with the non-core elements in anther stable set. Thus a model of pillage game with infinite stable sets must have this cyclic closure property. Once this is achieved, the logical impossibility of a dominance loop never returning to itself is removed. The remaining work is to find a specific function with the numerical characteristics that satisfies the above mentioned cyclic dominance structure conditions. Consider a continuous pillage game 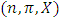 with non-empty core K. Let
with non-empty core K. Let 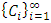 be a countably infinite set of allocations sets, each with finite cardinality. We can find a non-degenerate infinite sequence of allocations
be a countably infinite set of allocations sets, each with finite cardinality. We can find a non-degenerate infinite sequence of allocations 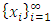 with
with 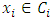 for each i. Since the total space of allocations X is compact, any non-degenerate infinite sequence in X contains a non-degenerate convergent subsequence. By an abuse of notation, we still denote this convergent subsequence by
for each i. Since the total space of allocations X is compact, any non-degenerate infinite sequence in X contains a non-degenerate convergent subsequence. By an abuse of notation, we still denote this convergent subsequence by 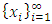 Denote the limit point of this convergent subsequence by
Denote the limit point of this convergent subsequence by 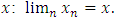 Since
Since 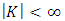 , elements in the core can be discarded from a non-degenerate infinite set of allocations. Thus we can assume
, elements in the core can be discarded from a non-degenerate infinite set of allocations. Thus we can assume 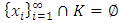 . We can filter this convergent subsequence further to give a non-degenerate subsequence monotone in each of the n coordinate indices
. We can filter this convergent subsequence further to give a non-degenerate subsequence monotone in each of the n coordinate indices 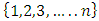 using a geometric filter as follows. In this context, monotonicity means for each of the index
using a geometric filter as follows. In this context, monotonicity means for each of the index 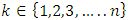 , the sequence of real numbers
, the sequence of real numbers 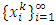 is either an increasing sequence of real numbers, or a decreasing sequence of real numbers, or a constant non-changing sequence consisting of a single real number. To apply the geometric filter, notice that for an arbitrary non-degenerate sequence of real numbers
is either an increasing sequence of real numbers, or a decreasing sequence of real numbers, or a constant non-changing sequence consisting of a single real number. To apply the geometric filter, notice that for an arbitrary non-degenerate sequence of real numbers 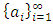 in
in 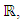 there is a monotone convergent subsequence. Thus for the convergent non-degenerate subsequence of allocations
there is a monotone convergent subsequence. Thus for the convergent non-degenerate subsequence of allocations 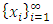 in
in 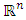 , we can find a monotone subsequence of
, we can find a monotone subsequence of 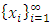 by passing to a monotone subsequence of real numbers in each one of the n coordinate indices starting with the first one. For example, if we denote the sequence of real numbers formed by the kth coordinate of all the allocations in the convergent sequence of allocations in its full multi-index expansion notation by
by passing to a monotone subsequence of real numbers in each one of the n coordinate indices starting with the first one. For example, if we denote the sequence of real numbers formed by the kth coordinate of all the allocations in the convergent sequence of allocations in its full multi-index expansion notation by 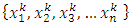 , then we can find a strictly monotone subsequence for this sequence of real numbers. We form a new convergent subsequence in the original convergent sequence of allocations
, then we can find a strictly monotone subsequence for this sequence of real numbers. We form a new convergent subsequence in the original convergent sequence of allocations 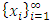 in
in 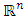 by including only those allocations for which the monotone subsequence is positioned. So for example, if every fourth element in the sequence of real numbers
by including only those allocations for which the monotone subsequence is positioned. So for example, if every fourth element in the sequence of real numbers 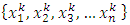 is discarded by this geometric filter, then every corresponding fourth element in the original sequence of convergent allocations
is discarded by this geometric filter, then every corresponding fourth element in the original sequence of convergent allocations 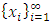 in
in  is discarded. An example of the geometric filter is given below. Example: consider the following non-degenerate infinite sequence of allocations in a 1-good 3-player pillage game:
is discarded. An example of the geometric filter is given below. Example: consider the following non-degenerate infinite sequence of allocations in a 1-good 3-player pillage game: 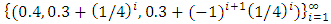 If we pass the sequence formed by the second coordinate through the geometric filter, then a monotone increasing convergent subsequence is achieved by selecting all the even terms
If we pass the sequence formed by the second coordinate through the geometric filter, then a monotone increasing convergent subsequence is achieved by selecting all the even terms 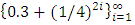 . The reader is cautioned that in doing so, not only are the odd terms in the sequence of real numbers formed by the second coordinate discarded, odd terms in the allocations are also discarded. Therefore, the geometric filter gives the following convergent subsequence, monotone in each of the three indices:
. The reader is cautioned that in doing so, not only are the odd terms in the sequence of real numbers formed by the second coordinate discarded, odd terms in the allocations are also discarded. Therefore, the geometric filter gives the following convergent subsequence, monotone in each of the three indices: 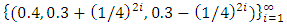 The reader is further cautioned that in the above example the second coordinate and the third coordinate are algebraically coupled. It is possible that in the original sequence of allocations
The reader is further cautioned that in the above example the second coordinate and the third coordinate are algebraically coupled. It is possible that in the original sequence of allocations 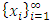 , one or more coordinates is already degenerate before we apply the geometric filter. That is, for a particular index k with
, one or more coordinates is already degenerate before we apply the geometric filter. That is, for a particular index k with 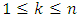 , the sequence
, the sequence 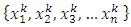 consists of only finitely many real numbers. In that case, we choose one real number for this index and retain all the terms in which this real number appears. Since the original sequence of allocations is non-degenerate, there is at least one index where the sequence of real numbers must consist of infinitely many non-equal real numbers. We start with the first index
consists of only finitely many real numbers. In that case, we choose one real number for this index and retain all the terms in which this real number appears. Since the original sequence of allocations is non-degenerate, there is at least one index where the sequence of real numbers must consist of infinitely many non-equal real numbers. We start with the first index 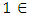
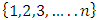 and repeat the process up to the nth index. Since there are only finitely many indices, the geometric filter will result in a convergent non-degenerate sequence monotone in each of the n indices. Due to numerous upper indices, lower indices, and the many filters, we still denote the resulting sequence of allocations as
and repeat the process up to the nth index. Since there are only finitely many indices, the geometric filter will result in a convergent non-degenerate sequence monotone in each of the n indices. Due to numerous upper indices, lower indices, and the many filters, we still denote the resulting sequence of allocations as 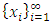 . Notice the filtered sequence has the property that in each coordinate
. Notice the filtered sequence has the property that in each coordinate 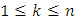 , each one of the following conditions holds:
, each one of the following conditions holds: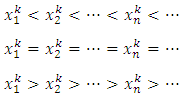 With this filtered sequence, we now consider a forward dominant structure where the more dominant allocations are the ones with higher indices:
With this filtered sequence, we now consider a forward dominant structure where the more dominant allocations are the ones with higher indices: 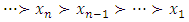
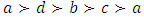 to show the non-uniqueness of stable sets [2]. Each of the above four elements is an “exceptional allocation” in the set
to show the non-uniqueness of stable sets [2]. Each of the above four elements is an “exceptional allocation” in the set 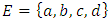 that dominates all other allocations in
that dominates all other allocations in 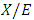 except for the elements in the core K. In their example, the power function has the special numerical property that it uses two different sets of double linear weights with the sum of 1, placed at three different coordinates to equalize the valuations for a and b and likewise for c and d. With these numerical constraints satisfied, the stable sets in this 1-good 4-player pillage game are
except for the elements in the core K. In their example, the power function has the special numerical property that it uses two different sets of double linear weights with the sum of 1, placed at three different coordinates to equalize the valuations for a and b and likewise for c and d. With these numerical constraints satisfied, the stable sets in this 1-good 4-player pillage game are 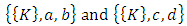 Hence a non-transitive forward dominance structure is carefully constructed using numerical analysis. This construction reveals certain intricate complexities that the simple order axioms set forth in the definition of pillage games allow. As such, special numerical analytic constructions can be achieved to allow for these “exotic” features of pillage games satisfying a set of rational and minimal expectations similar to the philosophical impasse in Arrow’s impossibility theorem. In contrast, our approach is a classic algebra-geometric approach where analytic concepts such as compactness and bounded convergence are used to derive the existence of sequences of allocations with special properties. Recall that the current convergent sequence of allocations is monotone in each of the n indices. With the above forward dominance structure, we haveLemma 1. There exists a subsequence of
Hence a non-transitive forward dominance structure is carefully constructed using numerical analysis. This construction reveals certain intricate complexities that the simple order axioms set forth in the definition of pillage games allow. As such, special numerical analytic constructions can be achieved to allow for these “exotic” features of pillage games satisfying a set of rational and minimal expectations similar to the philosophical impasse in Arrow’s impossibility theorem. In contrast, our approach is a classic algebra-geometric approach where analytic concepts such as compactness and bounded convergence are used to derive the existence of sequences of allocations with special properties. Recall that the current convergent sequence of allocations is monotone in each of the n indices. With the above forward dominance structure, we haveLemma 1. There exists a subsequence of 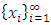 in the above setup such that for any subset C of
in the above setup such that for any subset C of 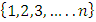 , only one of the following three mutually exclusive relations holds:
, only one of the following three mutually exclusive relations holds: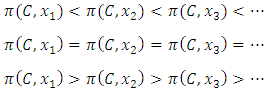 Proof. Since
Proof. Since 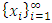 is strictly monotone in each index, if A is a subset of
is strictly monotone in each index, if A is a subset of 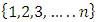 where the
where the 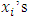 are increasing in their indices
are increasing in their indices 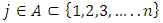 , then by the SR axiom, we have
, then by the SR axiom, we have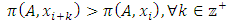
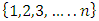 where the
where the  are decreasing in their indices
are decreasing in their indices 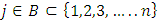 , then by the SR axiom, we have
, then by the SR axiom, we have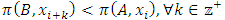
 where the
where the 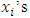 contain both increasing and decreasing indices, we use a unidirectionality filter to achieve monotonicity in
contain both increasing and decreasing indices, we use a unidirectionality filter to achieve monotonicity in 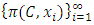 as follows. As a sequence of real numbers,
as follows. As a sequence of real numbers, 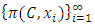 either consists of an infinitely many real numbers or it consists of only finitely many real numbers. If it is infinite, then
either consists of an infinitely many real numbers or it consists of only finitely many real numbers. If it is infinite, then 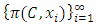 either contains a non-degenerate monotone increasing subsequence or a non-degenerate monotone decreasing subsequence. Assume without the loss of generality that
either contains a non-degenerate monotone increasing subsequence or a non-degenerate monotone decreasing subsequence. Assume without the loss of generality that 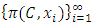 contains a monotone increasing subsequence. Then a new subsequence can be achieved by discarding the terms in
contains a monotone increasing subsequence. Then a new subsequence can be achieved by discarding the terms in 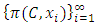 with indices j where the jth term in
with indices j where the jth term in 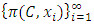 is not monotone increasing. We are then left with a non-degenerate subsequence of allocations
is not monotone increasing. We are then left with a non-degenerate subsequence of allocations 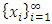 where for the subset
where for the subset 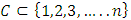 , the sequence of real numbers
, the sequence of real numbers 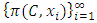 is a monotone increasing sequence. We still denote the newly filtered subsequence of allocations by
is a monotone increasing sequence. We still denote the newly filtered subsequence of allocations by 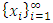 .If the sequence of real numbers
.If the sequence of real numbers 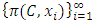 is a finite set, then we take the one of the valuations assumed by the power function restricted to the subset C. Notice because the geometrically filtered allocation sequence
is a finite set, then we take the one of the valuations assumed by the power function restricted to the subset C. Notice because the geometrically filtered allocation sequence 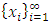 is monotone in each of the n indices, the first case where
is monotone in each of the n indices, the first case where 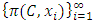 is an infinite set will occur by the SR axiom. Since there are only finitely many subsets of
is an infinite set will occur by the SR axiom. Since there are only finitely many subsets of 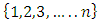 , after finitely many filtering steps, we arrive at a non-degenerate sequence of allocations, monotone in each index with the property that for each subset C of
, after finitely many filtering steps, we arrive at a non-degenerate sequence of allocations, monotone in each index with the property that for each subset C of 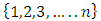 ,
, 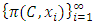 is a monotone sequence of real numbers. This completes the proof. The unidirectionality filter establishes a uniformity in the valuation by the power function with respect to any subset of
is a monotone sequence of real numbers. This completes the proof. The unidirectionality filter establishes a uniformity in the valuation by the power function with respect to any subset of 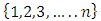 . We now consider the comparison of valuations by the power function with respect to any pair of non-empty and disjoint subsets of
. We now consider the comparison of valuations by the power function with respect to any pair of non-empty and disjoint subsets of 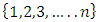 . For any pair of disjoint and non-empty sets
. For any pair of disjoint and non-empty sets 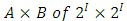 with
with 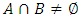 , we examine the sequence of equalities and inequalities that exists between
, we examine the sequence of equalities and inequalities that exists between 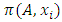 and
and 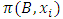 for the filtered allocation sequence
for the filtered allocation sequence 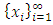 . We haveLemma 2. There exists a subsequence of
. We haveLemma 2. There exists a subsequence of 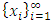 such that for each pair of disjoint and non-empty subsets
such that for each pair of disjoint and non-empty subsets  of
of 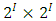 , only one of the following three mutually exclusive relations holds for all allocations in the sequence:
, only one of the following three mutually exclusive relations holds for all allocations in the sequence: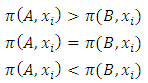 Proof. For each pair of disjoint non-empty subsets
Proof. For each pair of disjoint non-empty subsets 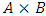 , at least one of the parity relations >, =, or < exists for infinitely many terms. It is certainly possible that two or all three parity relations exist for infinitely many terms in
, at least one of the parity relations >, =, or < exists for infinitely many terms. It is certainly possible that two or all three parity relations exist for infinitely many terms in 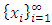 for a particular pair
for a particular pair 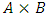 . We select a further subsequence of
. We select a further subsequence of 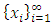 by the following parity comparison filter. If only one of the three above parity relations exists for infinitely many allocations in
by the following parity comparison filter. If only one of the three above parity relations exists for infinitely many allocations in 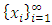 , then there are at most only finitely many allocations in the sequence where the other two parity relations exist. In this case, we filter
, then there are at most only finitely many allocations in the sequence where the other two parity relations exist. In this case, we filter 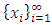 by discarding the finitely many terms for which the other two parity relations hold. For example, if for the pair
by discarding the finitely many terms for which the other two parity relations hold. For example, if for the pair 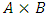 , all but finitely many terms in
, all but finitely many terms in  have
have 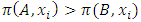 , then we discard the finitely terms where
, then we discard the finitely terms where 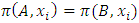 and
and 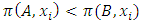 . If two or more of the above parity relations exist for infinitely many allocations in
. If two or more of the above parity relations exist for infinitely many allocations in 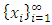 , then we select precisely one relation and discard the other allocations for which the chosen relation does not hold. Since there are only finitely many proper subsets of
, then we select precisely one relation and discard the other allocations for which the chosen relation does not hold. Since there are only finitely many proper subsets of 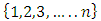 , there are only finitely many disjoint non-empty pairs of
, there are only finitely many disjoint non-empty pairs of 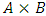 . Therefore the parity comparison filter will stop after all finitely many such pairs
. Therefore the parity comparison filter will stop after all finitely many such pairs 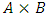 have been filtered, each resulting in an infinite non-degenerate subsequence of allocations. For the convenience of notations, we still denote the final filtered sequence of allocations as
have been filtered, each resulting in an infinite non-degenerate subsequence of allocations. For the convenience of notations, we still denote the final filtered sequence of allocations as 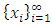 . This completes the proof. Recall that we denoted by x the limit point of the convergent allocation sequence
. This completes the proof. Recall that we denoted by x the limit point of the convergent allocation sequence 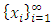 . We now prove a local regularity property of the filtered sequence. Theorem 3. There exists an
. We now prove a local regularity property of the filtered sequence. Theorem 3. There exists an 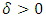 such that in an
such that in an 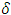 -neighborhood of x, the following equivalence of dominance structure holds:
-neighborhood of x, the following equivalence of dominance structure holds: 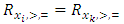
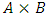 , the entire filtered sequence satisfies the same parity relations: <, =, or >. But these pairs of disjoint non-empty subsets A and B are precisely the pair of subsets that define the dominance relations for each allocation
, the entire filtered sequence satisfies the same parity relations: <, =, or >. But these pairs of disjoint non-empty subsets A and B are precisely the pair of subsets that define the dominance relations for each allocation 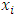 . That is, these pairs are precisely the pairs of subsets that define the win sets and lose sets for
. That is, these pairs are precisely the pairs of subsets that define the win sets and lose sets for 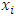 against any other allocation. For example, if
against any other allocation. For example, if 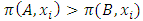 , then we have
, then we have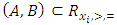
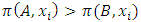 for all indices in the ultrafiltered sequence of allocations
for all indices in the ultrafiltered sequence of allocations 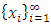 for each pair of disjoint non-empty subsets, then we have
for each pair of disjoint non-empty subsets, then we have 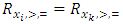 Notice the above equality relation may not hold true if we only have a convergent sequence of allocations approaching x. The three filters added a further rigidity to the original sequence of allocations such that in the end with the ultra-filtered sequence, these desired geometric and parity comparison properties hold. This completes the proof.We now summarize the three different filters from the above discussions in their prescribed order into an algorithm. The reader is reminded that because of the limit of mathematical notations, we still denote the filtered sequence by
Notice the above equality relation may not hold true if we only have a convergent sequence of allocations approaching x. The three filters added a further rigidity to the original sequence of allocations such that in the end with the ultra-filtered sequence, these desired geometric and parity comparison properties hold. This completes the proof.We now summarize the three different filters from the above discussions in their prescribed order into an algorithm. The reader is reminded that because of the limit of mathematical notations, we still denote the filtered sequence by 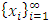 after each of the three filters. Given an infinite set of allocations
after each of the three filters. Given an infinite set of allocations 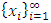 , the first filter is the geometric filter where we pass the original sequence through to achieve a subsequence monotone in each of the n coordinates. The second filter is the unidirectionality filter where for each proper subset
, the first filter is the geometric filter where we pass the original sequence through to achieve a subsequence monotone in each of the n coordinates. The second filter is the unidirectionality filter where for each proper subset 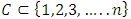 , an increasing, decreasing, or constant infinite subsequence of real numbers in
, an increasing, decreasing, or constant infinite subsequence of real numbers in 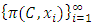 is selected. The third filter is the parity comparison filter where for each pair of disjoint non-empty subsets
is selected. The third filter is the parity comparison filter where for each pair of disjoint non-empty subsets 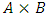 , we select an infinite subsequence in which only one of the three parity relations <, =, or > holds true all allocations in the chosen subsequence. This triple step algorithm gives an infinite sequence of allocations
, we select an infinite subsequence in which only one of the three parity relations <, =, or > holds true all allocations in the chosen subsequence. This triple step algorithm gives an infinite sequence of allocations  with the desired dominance relation properties. Notice in the forward dominance relation, we did not assume transitivity. That is, we did not assume
with the desired dominance relation properties. Notice in the forward dominance relation, we did not assume transitivity. That is, we did not assume 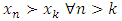 . But we will show that with our filtered sequence of allocations satisfying the geometric, the unidirectionality, and parity comparison relations, the forward dominance structure is in fact transitive. Theorem 4. The filtered sequence of allocations
. But we will show that with our filtered sequence of allocations satisfying the geometric, the unidirectionality, and parity comparison relations, the forward dominance structure is in fact transitive. Theorem 4. The filtered sequence of allocations 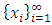 is transitively dominant:
is transitively dominant: 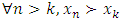 .Proof. Since
.Proof. Since 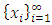 is strictly monotone in each coordinate, if i is an index where
is strictly monotone in each coordinate, if i is an index where 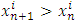 , then
, then 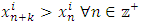 . Then by monotonicity, if
. Then by monotonicity, if  is the win set for
is the win set for  over
over  and
and 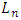 is the lose set for
is the lose set for 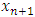 over
over 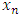 , then
, then 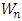 is also the win set for
is also the win set for 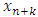 over
over 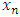 and
and 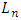 is also the lose set for
is also the lose set for  over
over 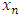 . Therefore we have
. Therefore we have 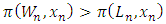 when
when 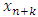 is compared to
is compared to 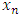 . But this is
. But this is 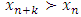 . This completes the proof.
. This completes the proof. 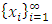 . Then different filters were used to reduce these allocations in order to achieve a convergent sequence with desired properties. In this section, we put these results together and examine a theoretical model that satisfies a set of conditions necessary for the existence of an infinite set of stable set.Since any stable set must have finite cardinality, the challenge in finding a model that makes an infinite set of stable sets possible is closing the dominance loop for any non-core allocations in a given allocation set
. Then different filters were used to reduce these allocations in order to achieve a convergent sequence with desired properties. In this section, we put these results together and examine a theoretical model that satisfies a set of conditions necessary for the existence of an infinite set of stable set.Since any stable set must have finite cardinality, the challenge in finding a model that makes an infinite set of stable sets possible is closing the dominance loop for any non-core allocations in a given allocation set 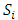 against the non-core allocations in another set
against the non-core allocations in another set 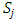 for a countably infinite family of such sets. This implies when comparing two distinct allocation sets
for a countably infinite family of such sets. This implies when comparing two distinct allocation sets 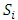 and
and 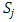 , any chain of dominance starting with a non-core allocation in
, any chain of dominance starting with a non-core allocation in 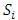 must end after finitely many allocations with a non-core allocation in the same set
must end after finitely many allocations with a non-core allocation in the same set 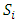 in order for
in order for 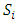 to satisfy external stability against
to satisfy external stability against 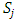 :
: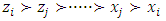 with
with 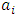 and
and 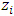 in
in 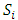 and
and 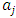 and
and 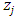 in
in 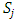 . Since this relation must also hold true for
. Since this relation must also hold true for 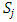 against
against 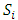 , a necessary condition is the existence of two distinct sets of allocations. Since this second set of allocations consists of non-core elements, dominance structures also exist within these allocations. Let
, a necessary condition is the existence of two distinct sets of allocations. Since this second set of allocations consists of non-core elements, dominance structures also exist within these allocations. Let 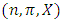 be a continuous pillage game with a non-empty core K. Suppose we have an infinite sequence of forward dominant allocations
be a continuous pillage game with a non-empty core K. Suppose we have an infinite sequence of forward dominant allocations 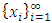 satisfying the monotonicity, unidirectionality, and parity comparison conditions in section 4. This implies that two distinct allocations
satisfying the monotonicity, unidirectionality, and parity comparison conditions in section 4. This implies that two distinct allocations 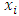 and
and 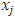 can belong to two distinct sets
can belong to two distinct sets 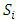 and
and 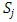 to satisfy internal stability. Let K and
to satisfy internal stability. Let K and 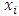 be in
be in 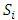 . By theorem 4,
. By theorem 4, 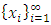 is transitively dominant. External stability necessitates allocations
is transitively dominant. External stability necessitates allocations 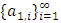 that dominate
that dominate 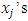 down the chain by theorem 2. In the notation
down the chain by theorem 2. In the notation 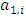 , the first right index 1 indicates that this sequence of allocations
, the first right index 1 indicates that this sequence of allocations 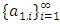 is the first sequence needed after the original sequence
is the first sequence needed after the original sequence 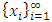 . The second right index i indicates the position of the element
. The second right index i indicates the position of the element 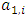 in the set of allocations. Namely,
in the set of allocations. Namely, 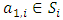 . Thus we have for
. Thus we have for 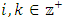
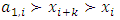 Lemma 3.
Lemma 3. 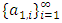 is a sequence of pairwise distinct allocations. That is,
is a sequence of pairwise distinct allocations. That is, 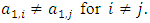 Proof. Suppose for
Proof. Suppose for 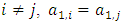 . Assume without the loss of generality that
. Assume without the loss of generality that 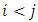 . Since
. Since 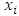 and
and 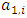 are in
are in 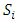 and
and 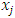 and
and 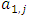 are in
are in 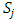 , forward dominance of
, forward dominance of 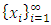 implies that we have
implies that we have 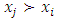 By external stability of
By external stability of 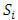 , we also have
, we also have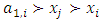 Since
Since 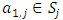 , if
, if 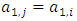 , the dominance sequence above implies that
, the dominance sequence above implies that 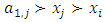 But this contradicts the internal stability of
But this contradicts the internal stability of 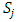 . Thus we must have
. Thus we must have 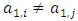 for
for 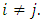 This completes the proof. The above lemma implies that an infinite sequence of allocations
This completes the proof. The above lemma implies that an infinite sequence of allocations 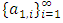 where
where 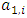 dominates an infinite subset of
dominates an infinite subset of 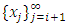 is needed to ensure external stability. Thus we have that K,
is needed to ensure external stability. Thus we have that K, 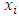 and
and 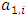 now belong to
now belong to 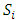 . Since we have
. Since we have 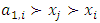 and
and 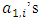 are non-core allocations, there is an allocation in
are non-core allocations, there is an allocation in 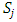 that dominates
that dominates 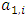 . This necessitates the existence of a second sequence of allocations
. This necessitates the existence of a second sequence of allocations 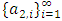 with
with 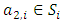 . We now consider a set of conditions sufficient for the existence of an
. We now consider a set of conditions sufficient for the existence of an 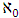 -order set of stable sets in a continuous pillage game: 1.
-order set of stable sets in a continuous pillage game: 1. 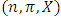 contains pairwise distinct forward dominant sequences
contains pairwise distinct forward dominant sequences 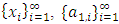 , and
, and 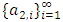 in the interior of X such that each sequence satisfies the conditions of monotonicity, unidirectionality, and parity comparison. 2. There exists a finite set of non-core allocations
in the interior of X such that each sequence satisfies the conditions of monotonicity, unidirectionality, and parity comparison. 2. There exists a finite set of non-core allocations 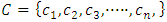 with
with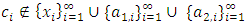 ;
; 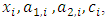 and elements in K do not dominate each other; and
and elements in K do not dominate each other; and 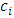 does not dominate
does not dominate 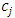 for
for 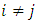 .3.
.3. 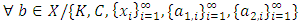 , b is either dominated by a subset of the core, or by allocations in C, or by an allocation in
, b is either dominated by a subset of the core, or by allocations in C, or by an allocation in 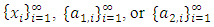 for each i. 4. The following inter-sequence dominance structure holds
for each i. 4. The following inter-sequence dominance structure holds 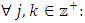
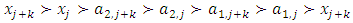 Theorem 6. A continuous pillage game with a power function
Theorem 6. A continuous pillage game with a power function 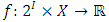 satisfying the three order axioms and conditions (1) through (4) contains an
satisfying the three order axioms and conditions (1) through (4) contains an 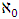 -order of stable sets
-order of stable sets 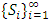 with
with 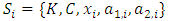 .Proof. Let
.Proof. Let 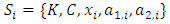 . Condition (1) gives the infinite sequences where valuation comparisons can be made by the power function. These sequences satisfy the conditions of monotonicity, unidirectionality, and parity comparison. Forward dominant means that
. Condition (1) gives the infinite sequences where valuation comparisons can be made by the power function. These sequences satisfy the conditions of monotonicity, unidirectionality, and parity comparison. Forward dominant means that 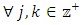 , we have the following relations:
, we have the following relations: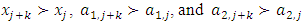
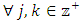 , any non-core allocation in
, any non-core allocation in 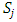 gives a unique chain of dominance that ends also in
gives a unique chain of dominance that ends also in 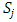 . For
. For 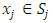 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: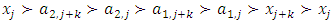
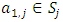 , conditions (1) and (4) also give the following finite chain of dominance:
, conditions (1) and (4) also give the following finite chain of dominance: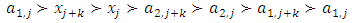
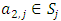 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: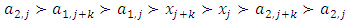
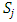 with
with 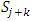 , if we start with any non-core allocation in
, if we start with any non-core allocation in 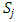 , the chain of dominance structure is always a cyclic loop of finite length that ends in a non-core allocation in
, the chain of dominance structure is always a cyclic loop of finite length that ends in a non-core allocation in 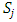 to ensure external stability. Starting with any non-core allocation in
to ensure external stability. Starting with any non-core allocation in 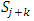 , conditions (1) and (4) also give a chain of finite length against non-core allocations in
, conditions (1) and (4) also give a chain of finite length against non-core allocations in 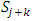 . For
. For 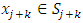 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: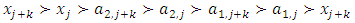
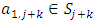 , conditions (1) and (4) also give the following finite chain of dominance:
, conditions (1) and (4) also give the following finite chain of dominance: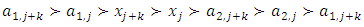
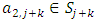 , conditions (1) and (4) give the following finite chain of dominance:
, conditions (1) and (4) give the following finite chain of dominance: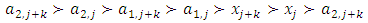
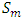 and
and 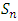 , starting with any non-core allocation in the first stable set
, starting with any non-core allocation in the first stable set 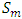 , a dominance loop of finite length ending also with an allocation in
, a dominance loop of finite length ending also with an allocation in 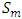 exists both for
exists both for 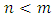 and
and 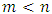 . Condition (2) gives internal stability in that for any pair of allocations a and b in
. Condition (2) gives internal stability in that for any pair of allocations a and b in 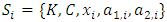 , if we denote
, if we denote 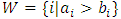 and
and 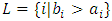 , then we have
, then we have 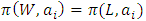 and
and 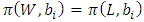 . Condition (3) gives external stability for
. Condition (3) gives external stability for 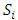 . The reader is cautioned that the theorem only gives a special set of sufficient conditions – these conditions may not be necessary. Indeed there can be numerous examples of pillage games in which conditions other than conditions (1) through (4) are satisfied but still have infinitely many stable sets.
. The reader is cautioned that the theorem only gives a special set of sufficient conditions – these conditions may not be necessary. Indeed there can be numerous examples of pillage games in which conditions other than conditions (1) through (4) are satisfied but still have infinitely many stable sets. 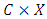 is a compact set for any
is a compact set for any 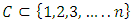 , its image
, its image 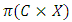 is also a compact set in
is also a compact set in 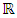 . Hence
. Hence 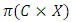 is a bounded set. In addition, since a continuous function on a compact set is also uniformly continuous,
is a bounded set. In addition, since a continuous function on a compact set is also uniformly continuous, 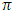 is uniformly continuous on
is uniformly continuous on 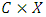 . These rich structural properties lead to a simpler path of analysis of continuous pillage games. We now propose two possible future approaches to the study of pillage games, one for the continuous case and the other for the general case without the assumption of continuity. If a pillage game is continuous, the boundedness property and the subsequent uniform continuity property stated above allow for a profile of
. These rich structural properties lead to a simpler path of analysis of continuous pillage games. We now propose two possible future approaches to the study of pillage games, one for the continuous case and the other for the general case without the assumption of continuity. If a pillage game is continuous, the boundedness property and the subsequent uniform continuity property stated above allow for a profile of 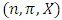 to be constructed as follows. Given any
to be constructed as follows. Given any 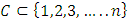 and
and 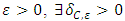 depending on
depending on 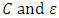 such that
such that 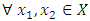 with
with 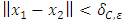 , we have
, we have 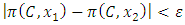 . Since there are only finitely many subsets of
. Since there are only finitely many subsets of 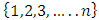 , a lower bound on all of the
, a lower bound on all of the 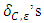 with C spanning
with C spanning 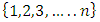 can be found. As a result, the power function’s growth rate can be controlled. Thus starting at any allocation x, one can ask: what is the maximum rate a coalition C’s collective power can grow by moving to a nearby allocation x’. In the general case without the assumption of continuity, notice that pillage games have certain measure-theoretic properties that give insights and characterize classes of games beyond pillage games. Given an allocation x, the WC condition introduces a property similar to that of a measure
can be found. As a result, the power function’s growth rate can be controlled. Thus starting at any allocation x, one can ask: what is the maximum rate a coalition C’s collective power can grow by moving to a nearby allocation x’. In the general case without the assumption of continuity, notice that pillage games have certain measure-theoretic properties that give insights and characterize classes of games beyond pillage games. Given an allocation x, the WC condition introduces a property similar to that of a measure 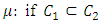 , then
, then 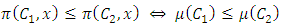
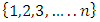 , a binary relation with respect to set inclusion exists. One needs to use caution in that if
, a binary relation with respect to set inclusion exists. One needs to use caution in that if 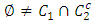 and
and 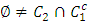 , no conclusion can be made on the comparison of
, no conclusion can be made on the comparison of 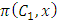 and
and 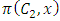 . One can obtain certain quantitative comparisons because the following set inclusion holds:
. One can obtain certain quantitative comparisons because the following set inclusion holds: 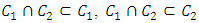 , and
, and 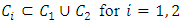 .From the other end, given
.From the other end, given 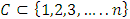 . the WR and SR conditions also impose a poset structure
. the WR and SR conditions also impose a poset structure  on allocations in X as follows. If
on allocations in X as follows. If 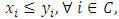 then
then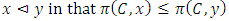
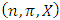 , one cannot compare
, one cannot compare 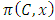 to
to 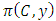 if
if 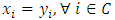 . But these above stated properties indeed make
. But these above stated properties indeed make 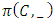 a “semi-poset”
a “semi-poset”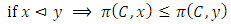
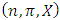 displays properties of a fibre bundle. That is,
displays properties of a fibre bundle. That is, 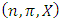 can be considered as a map on the cross product
can be considered as a map on the cross product 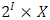 that fibers over the subsets of
that fibers over the subsets of 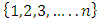 . Given a subset
. Given a subset 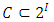 , the fibering respects set inclusions. Conversely, when restricted to a particular subset, the fibre splitting respects the poset structure stated above. Given these observations, the following question can be asked: is there a general form of representation theorem for pillage games? In other words, can there exist a real-valued function
, the fibering respects set inclusions. Conversely, when restricted to a particular subset, the fibre splitting respects the poset structure stated above. Given these observations, the following question can be asked: is there a general form of representation theorem for pillage games? In other words, can there exist a real-valued function 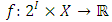 and a semi-measure
and a semi-measure 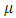 such that given
such that given 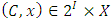 , we have
, we have 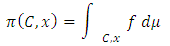
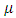 exists on
exists on 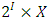 such that the power function
such that the power function 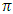 can be represented as the integral of this
can be represented as the integral of this  -measurable real-valued function f, the integral of f could be unbounded over the product space
-measurable real-valued function f, the integral of f could be unbounded over the product space 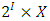 :
: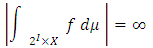
 .
.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML