Irinel Dragan
University of Texas, Mathematics, Arlington, Texas, USA
Correspondence to: Irinel Dragan, University of Texas, Mathematics, Arlington, Texas, USA.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In earlier works, we discussed the Inverse Problem for Binomial Semivalues, with coalitional rationality, and the use of Flow Games in the Gas Routing Problem. In the present paper, we apply the techniques shown in connection with the first problems, to the second class of practical problems of cooperation in the gas routing activity.
Keywords:
Game Theory, Inverse Problem, Coalitional rationality, Binomial Semivalues, Flow Games
Cite this paper: Irinel Dragan, Binomial Semivalues, the Inverse Problem and the Gas Routing, Journal of Game Theory, Vol. 7 No. 1, 2018, pp. 17-21. doi: 10.5923/j.jgt.20180701.03.
1. Introduction
In a cooperative transferable utilities game 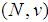 , where the finite set N is the set of players, and
, where the finite set N is the set of players, and 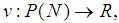 with
with 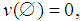 is the characteristic function, defined on
is the characteristic function, defined on 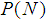 , the Power Set of N we have a classical problem: assuming that the grand coalition has been formed, how do we allocate to the individual players the win
, the Power Set of N we have a classical problem: assuming that the grand coalition has been formed, how do we allocate to the individual players the win 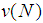 of the grand coalition? Usually, the allocation is done by means of one of the values, the Egalitarian Value, the Shapley Value, the Normalized Banzhaf Value, the Normalized Semivalues, etc. All these values have nice properties, in some cases used as a group of axioms defining uniquely the value. There are two main cases: efficient values and non efficient values, that should be normalized in order to get an allocation. However, recall that for each coalition S, a non-empty subset of N, the worth
of the grand coalition? Usually, the allocation is done by means of one of the values, the Egalitarian Value, the Shapley Value, the Normalized Banzhaf Value, the Normalized Semivalues, etc. All these values have nice properties, in some cases used as a group of axioms defining uniquely the value. There are two main cases: efficient values and non efficient values, that should be normalized in order to get an allocation. However, recall that for each coalition S, a non-empty subset of N, the worth 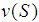 is the total win that the members of S can share, whatever action take the other players not in S. Assuming that an allocation
is the total win that the members of S can share, whatever action take the other players not in S. Assuming that an allocation 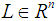 of
of 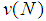 has been decided, it is natural that for all coalitions
has been decided, it is natural that for all coalitions 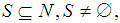 the total win of members of S should be at least equal to
the total win of members of S should be at least equal to 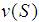 . Hence, we should have
. Hence, we should have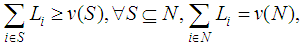 | (1) |
that is the allocation belongs to the Core of the game, i.e. it is Coalitional Rational. However, it is well known that even the Shapley Value of a game does not belong always to the Core of the game. In this way, occurs the problem: for a given vector L, find out some games for which we have 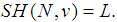 The set of all games solutions of this problem, introduced and determined in [1], was called the Inverse Set, relative to the Shapley Value. Of course, a second connected problem occurs: for a given vector L, find out some games in the Inverse Set, with the Shapley Value in the Core. How do you solve this problem, for the case of the Shapley Value and the Banzhaf Value is discussed in [2] and [3], and for the Semivalues in [4]. The two cases, efficient and non efficient Semivalues are presented, by introducing also the concept of coalitional rationality in the last case. Now, an interesting new value has been introduced by A.Puente in [5], called the Binomial Semivalue, and we discussed in [6] the two problems above, relative to this value. In an earlier work, [7], we were modeling the gas routing problem as a game theoretic problem, by using the ideas introduced by Kalai/Zemel in [8], and we discussed the Inverse Problem, relative to Binomial Semivalues. In the present paper, the Inverse Problem relative to these values, with Coalitional Rationality, is discussed as follows. In the second section, the model of Gas Routing is presented, by taking a numerical example, where the numbers are taken arbitrarily by the author. The results of the earlier work connected to the Inverse Problem with Coalitional Rationality, relative to the Shapley Value, were applied to the Flow Game in the third section. The results on the Inverse Problem with Coalitional Rationality, relative to the Semivalues, are applied in the fourth section to the Binomial Semivalues of the Game obtained earlier in the Gas Routing, and a solution for the two problems is given in this case. Discussions about some special situations that may occur in connection to the Gas Routing model are carried in the last section.
The set of all games solutions of this problem, introduced and determined in [1], was called the Inverse Set, relative to the Shapley Value. Of course, a second connected problem occurs: for a given vector L, find out some games in the Inverse Set, with the Shapley Value in the Core. How do you solve this problem, for the case of the Shapley Value and the Banzhaf Value is discussed in [2] and [3], and for the Semivalues in [4]. The two cases, efficient and non efficient Semivalues are presented, by introducing also the concept of coalitional rationality in the last case. Now, an interesting new value has been introduced by A.Puente in [5], called the Binomial Semivalue, and we discussed in [6] the two problems above, relative to this value. In an earlier work, [7], we were modeling the gas routing problem as a game theoretic problem, by using the ideas introduced by Kalai/Zemel in [8], and we discussed the Inverse Problem, relative to Binomial Semivalues. In the present paper, the Inverse Problem relative to these values, with Coalitional Rationality, is discussed as follows. In the second section, the model of Gas Routing is presented, by taking a numerical example, where the numbers are taken arbitrarily by the author. The results of the earlier work connected to the Inverse Problem with Coalitional Rationality, relative to the Shapley Value, were applied to the Flow Game in the third section. The results on the Inverse Problem with Coalitional Rationality, relative to the Semivalues, are applied in the fourth section to the Binomial Semivalues of the Game obtained earlier in the Gas Routing, and a solution for the two problems is given in this case. Discussions about some special situations that may occur in connection to the Gas Routing model are carried in the last section.
2. The Flow Games and the Gas Routing
In some area it has been discovered a source of natural gas; several companies rushed to build drilling facilities, in order to take this fantastic opportunity for profits. Suppose that there were three competitors, who succeeded to lease mineral rights and got the drilling started at points A, B, and C, respectively. The gas should be routed to a central depot, where another company will buy it and start the deliveries to consumers. The companies were supposed to have ducts from the points of drilling to the depot, but they were not allowed to build parallel ducts on the city streets. In this way, by using their connections, they built a network, that may be represented by a graph with capacities, described by the matrix called the adjacency matrix. The set of vertices of the graph is 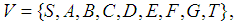 where S is a unique source, T is a unique sink, then
where S is a unique source, T is a unique sink, then 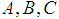 are the drilling vertices, and the three companies denoted by
are the drilling vertices, and the three companies denoted by 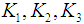 own the sets of ducts
own the sets of ducts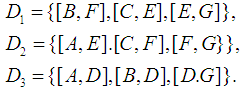 The capacities of the ducts are given by the matrix
The capacities of the ducts are given by the matrix in which the rows for G and T, as well as the columns for S and T, were omitted being almost empty, except
in which the rows for G and T, as well as the columns for S and T, were omitted being almost empty, except 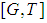 a public duct with capacity 25, used for entering the depot. Of course, in general there may be several public ducts. The capacities of the auxiliary ducts
a public duct with capacity 25, used for entering the depot. Of course, in general there may be several public ducts. The capacities of the auxiliary ducts 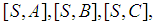 are derived from the number of units of gas obtained per time unit by drilling, while the companies are choosing the overall routing by cooperation. The data were arbitrarily taken by the author. The Flow Game associated to various groups of cooperating players, following the Kalai/Zemel paper [8], who introduced the concept, is the cooperative TU game
are derived from the number of units of gas obtained per time unit by drilling, while the companies are choosing the overall routing by cooperation. The data were arbitrarily taken by the author. The Flow Game associated to various groups of cooperating players, following the Kalai/Zemel paper [8], who introduced the concept, is the cooperative TU game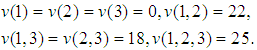 | (2) |
Now, the individual allocation of production for the companies will be given by an efficient value, or by the normalization of a non efficient value. In two earlier papers (Dragan, [2], [3]), the allocations were given by the two most famous Semivalues: the Shapley Value and the Banzhaf Value. We got | (3) |
As it is easy to see, both values do not belong to the Core of the game. The first is efficient, as the sum of allocations makes 25, but for any coalition of size 2, the Core condition does not hold. The second is not even efficient and if we compute the additive normalization we get 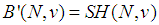 efficient, that is not in the Core. Then, we used the Inverse Problem for Semivalues, the problem we introduced and solved earlier (Dragan, [4]). In the efficient case, we stated the problem as follows: given the vector L, find out the set of all games with the same set N, of players for which we have
efficient, that is not in the Core. Then, we used the Inverse Problem for Semivalues, the problem we introduced and solved earlier (Dragan, [4]). In the efficient case, we stated the problem as follows: given the vector L, find out the set of all games with the same set N, of players for which we have 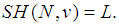 This set was called the Inverse Set, relative to the Shapley Value, and it was given by
This set was called the Inverse Set, relative to the Shapley Value, and it was given by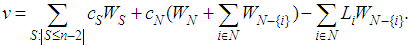 | (4) |
Here we have a basis of the vector space of all games with the set of players N, denoted by 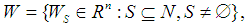 where for all coalitions
where for all coalitions 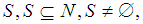 we have
we have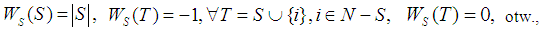 | (5) |
with the arbitrary constants 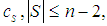 and
and 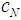 . Now, we want to get a Semivalue which is a Coalitional rational value. In the Inverse Set, we considered the family of games called the almost null family, obtained for all
. Now, we want to get a Semivalue which is a Coalitional rational value. In the Inverse Set, we considered the family of games called the almost null family, obtained for all 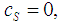 while we kept only the unique parameter
while we kept only the unique parameter 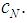 Then, we imposed the condition that the games belong to the Core, from which we got the inequality
Then, we imposed the condition that the games belong to the Core, from which we got the inequality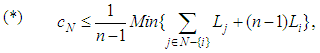 Now, if we take the last parameter to satisfy the inequality and write component wise the almost null family, we get a game with the previously given Shapley Value, that has the value in the Core. For example, in our flow game, associated with the gas routing problem, the inequality (*) is
Now, if we take the last parameter to satisfy the inequality and write component wise the almost null family, we get a game with the previously given Shapley Value, that has the value in the Core. For example, in our flow game, associated with the gas routing problem, the inequality (*) is 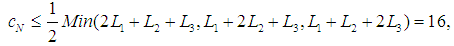 | (6) |
So that, by using the formulas derived from the games in the Inverse Set, when we take 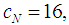 we obtain the game solution
we obtain the game solution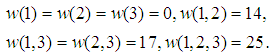 | (7) |
In the non efficient case, the two problems are more difficult, because the solution is not even an allocation. For the Inverse Set, relative to a Binomial Semivalue, we have a very similar expansion, but with a more general potential basis (see [8]), as it will be seen below. Then, we shall introduce an allocation, by working on the Power Game in the Inverse Set, where the coalitional rationality is defined by means of the Power Core, the Core of the Power Game.
3. Binomial Semivalues and the Inverse Problem
The Semivalues, axiomatically introduced by Dubey, Neyman and Weber in [9], in the TU case may be defined by means of the formula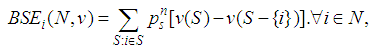 | (8) |
where the weight vector satisfies the normalization condition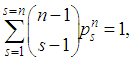 | (9) |
and the weight vectors for the subgames are obtained for all 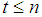 from the recursive formula
from the recursive formula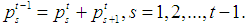 | (9)’ |
These were called the Inverse Pascal triangle conditions. The Binomial Semivalues were introduced by A.Puente in [5]. These are the values that have weight vectors satisfying beside (9) the new conditions: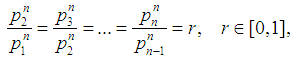 | (10) |
or, by combining (8) and (9): 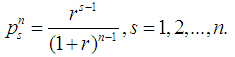 | (11) |
If we replace (11) in the definition of the Binomial Semivalue, (8), then a computational formula is obtained: 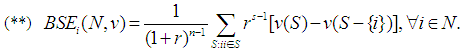 For the Flow Game, shown in the previous section, if we use
For the Flow Game, shown in the previous section, if we use 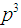 derived from (11), this formula (**) and the characteristic function (2), we get the Binomial Semivalue of this game:
derived from (11), this formula (**) and the characteristic function (2), we get the Binomial Semivalue of this game: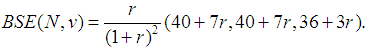 | (12) |
The sum of the components makes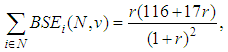 | (13) |
hence, in general, the value is not efficient. We proceed like above, starting with the Inverse Problem, relative to the Semivalue (see [6]), that is we use another, more general, basis  | (14) |
defined by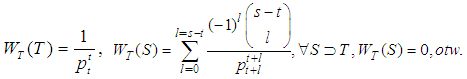 | (15) |
The expansion for the Inverse Set with the new basis looks like (4) above, where now this new basis is used and the Binomial Semivalue is replacing the Shapley Value. Further, we derive the family of almost null games in the Inverse Set, by taking the constants equal to zero, except the potential of the game,  Further, it occurs the fact that, in general, for any value of the parameter
Further, it occurs the fact that, in general, for any value of the parameter  , in terms of r, the games
, in terms of r, the games  in this family have the Binomial Semivalue the same as the previous one, but this is not efficient, in general; hence, it does not belong to the Core. Therefore, as shown in [6], we shall consider the so called Power Game
in this family have the Binomial Semivalue the same as the previous one, but this is not efficient, in general; hence, it does not belong to the Core. Therefore, as shown in [6], we shall consider the so called Power Game 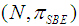 for the games in the almost null family denoted with
for the games in the almost null family denoted with 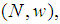 by using for all subgames
by using for all subgames 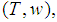 the definition
the definition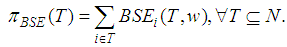 | (16) |
Note that it is easier to use in the computation of the Power Game, a formula proved in [10], because for the moment, we should compute only the worth of the characteristic function for the coalitions of size 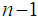 . The games in the almost null family are offered by the expansion
. The games in the almost null family are offered by the expansion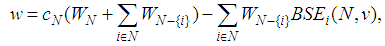 | (17) |
with the new basis. If we write it in scalar form, we get the formulas for the family of games in the almost null family: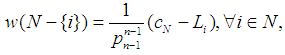 | (18) |
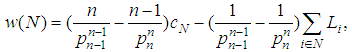 | (19) |
where we notice that these games will depend also on the weights of the Binomial Semivalue. In particular, the efficiency is in general missing. The omitted worth of the characteristic function are zero. Replacing in (18) and (19) the weights offered by (11), we get the family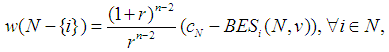 | (20) |
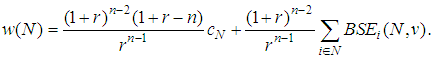 | (21) |
Here the other worth of the characteristic function are zero. It is only a simple computation to prove that this game has the same Binomial Semivalue as the given one, for any value of r. For our Flow Game with 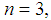 we obtain the family of games
we obtain the family of games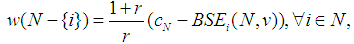 | (22) |
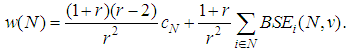 | (23) |
Of course, we can replace here the values shown in (12). However, it remains undetermined the value of the parameter 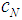 , which will be a function of r, selected such that the Binomial Semivalue is coalitional rational, and this will be done in the next section.
, which will be a function of r, selected such that the Binomial Semivalue is coalitional rational, and this will be done in the next section.
4. Power Game and Coalitional Rationality
Recall from [6], that by definition a Semivalue is coalitional rational, if it will belong to the Core of the Power Game. If the Semivalue is already efficient, it remains to impose only the conditions on the worth of characteristic function for coalitions of size 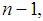 for the games in the Inverse Set. Otherwise, first we should compute the games in the Inverse Set, then
for the games in the Inverse Set. Otherwise, first we should compute the games in the Inverse Set, then 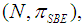 the Power Game of the games from the almost null family
the Power Game of the games from the almost null family 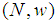 shown in the previous section. We use the definition (16), in which the coalitions T have the size
shown in the previous section. We use the definition (16), in which the coalitions T have the size 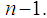 The worth of coalitions of size
The worth of coalitions of size 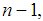 in the Power Game, derived from (16), based upon (22) are
in the Power Game, derived from (16), based upon (22) are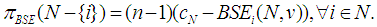 | (24) |
The coalitional rationality conditions are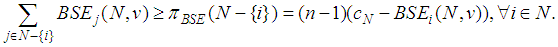 | (25) |
Together, these conditions may be written as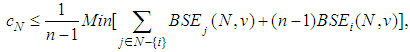 | (26) |
where the minimum is taken over i. Notice that this looks exactly like (*), which is the formula for the efficient values.For our example, with 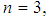 we get:
we get: 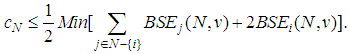 | (27) |
Now we may compute the right hand side in (27), to get the coalitional rationality condition for our Flow Game. A simple computation, by using (12) in (27), would give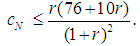 | (28) |
Note that there is an infinite set of games with the same Binomial Semivalue like the given Flow Game, and for which this is coalitional rational. There is also an infinite set of games with this Binomial Semivalue but for which this is not coalitional rational. To get one of the solution games, taking into account that 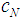 is the potential of the game, let us choose for the parameter, the highest value satisfying (28). A simple computation gives many solutions for our problem, in the Inverse Set, in fact the family of almost null games. We obtain the games:
is the potential of the game, let us choose for the parameter, the highest value satisfying (28). A simple computation gives many solutions for our problem, in the Inverse Set, in fact the family of almost null games. We obtain the games: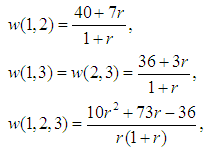 | (29) |
The Power Games of the games (29), computed by using the definition (16), will be: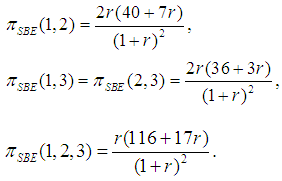 | (30) |
It is a simple exercise to check that the Binomial Semivalues of the games (29) equal the Binomial Semivalue of the Flow Game, and this value belongs to the Core of the games (30), hence it is a solution of our problem, for any value of the parameter r.We may still make a new application: take the parameter equal to 1, that is consider the Banzhaf Value, and get all results obtained earlier in [3]. We note that in our present paper, we have the formulas (29), valid for the Semivalues corresponding to all the values of the parameter r. Note that the solution (29) gives more than one game, so that we have some freedom to select any flow game obtained for any value of the parameter.
5. Conclusions
In the present paper, we have shown the model of a Flow Game for the Gas Routing Problem discussed in the second section, and we obtained the cooperative transferable utilities game: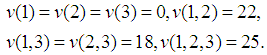 | (31) |
We computed the Binomial Semivalue of this game and we obtained the value shown in the third section: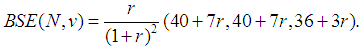 | (32) |
We notice that this value is non efficient, in general, so that we have first to compute the family of almost null games in the Inverse Set, relative to the Binomial Semivalue, shown in the fourth section. Then, to compute the Power Game and derive the condition of coalitional rationality, which was also done in the same section. Further, we selected a value for 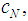 the parameter of the games in the almost null family, namely the highest value possible, and we computed the solution game for the given Flow Game associated to the gas routing problem:
the parameter of the games in the almost null family, namely the highest value possible, and we computed the solution game for the given Flow Game associated to the gas routing problem: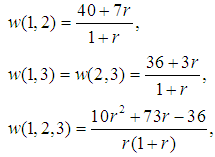 | (33) |
where we have null worth for the singletons. It is easy to compute the Binomial Semivalue for the games (33), to show that this is (32), and this belongs to the Power Core. The normalization of the games (33) is a solution for our practical problem. Notice that in the case of these values, we obtain an entire family of solutions, a fact useful in practical matters.
ACKNOWLEDGEMENTS
Note that the present work is an application of the theory developed in the earlier paper [6] to the problems of type [7]. Of course, we may have more than three companies competing for the exploration of the source of gas, or another similar product.
References
| [1] | Dragan, I., (1991), The potential basis and the weighted Shapley Value, Libertas Mathematica 11, 138-146. |
| [2] | Dragan, I., (2014), On the coalitional rationality of the Shapley Value and other efficient values of cooperative TU games, AJOR, 4, 328-334. |
| [3] | Dragan, I., (2015), On the coalitional rationality of the Banzhaf Value and other non efficient values of cooperative TU games, Appl. Math., 6, 2069-2076. |
| [4] | Dragan, I., (2005), On the Inverse Problem for Semivalues of cooperative TU games, IJPAM, 22, 545-561. |
| [5] | Puente, A., (2000), Contributions to the representabilty of simple games, and to the calculus of solutions for this class of games, Ph.D. Thesis, Univ. Catalonia, Barcelona, Spain. |
| [6] | Dragan, I., (2014), On the Inverse Problem and the coalitional rationality for Binomial Semivalues of cooperative TU games, in Contributions to Game Theory and Management, L. Petrosjan and N. Zenkevich, (eds.), St. Petersburg University, Russia, 7, 24-33. |
| [7] | Dragan, I., (2015), On the gas routing via Game Theory, AJOR, 5, 288-292. |
| [8] | Kalai, E., and Zemel, R., (1982), On totally balanced games and games of flow, Math. O.R., 7, 476-478. |
| [9] | Dubey, P., Neyman, A., and Weber, R.J., (1982), Value theory without efficiency, Math. O.R., 6, 122-128. |
| [10] | Dragan, I., and Martinez-Legaz, J.E., (2001), On the Semivalues and the Power Core of cooperative TU games, IGTR, 3, 127-139. |



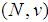 , where the finite set N is the set of players, and
, where the finite set N is the set of players, and 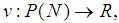 with
with 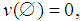 is the characteristic function, defined on
is the characteristic function, defined on 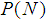 , the Power Set of N we have a classical problem: assuming that the grand coalition has been formed, how do we allocate to the individual players the win
, the Power Set of N we have a classical problem: assuming that the grand coalition has been formed, how do we allocate to the individual players the win 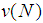 of the grand coalition? Usually, the allocation is done by means of one of the values, the Egalitarian Value, the Shapley Value, the Normalized Banzhaf Value, the Normalized Semivalues, etc. All these values have nice properties, in some cases used as a group of axioms defining uniquely the value. There are two main cases: efficient values and non efficient values, that should be normalized in order to get an allocation. However, recall that for each coalition S, a non-empty subset of N, the worth
of the grand coalition? Usually, the allocation is done by means of one of the values, the Egalitarian Value, the Shapley Value, the Normalized Banzhaf Value, the Normalized Semivalues, etc. All these values have nice properties, in some cases used as a group of axioms defining uniquely the value. There are two main cases: efficient values and non efficient values, that should be normalized in order to get an allocation. However, recall that for each coalition S, a non-empty subset of N, the worth 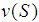 is the total win that the members of S can share, whatever action take the other players not in S. Assuming that an allocation
is the total win that the members of S can share, whatever action take the other players not in S. Assuming that an allocation 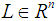 of
of 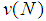 has been decided, it is natural that for all coalitions
has been decided, it is natural that for all coalitions 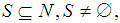 the total win of members of S should be at least equal to
the total win of members of S should be at least equal to 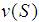 . Hence, we should have
. Hence, we should have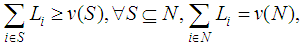
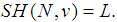 The set of all games solutions of this problem, introduced and determined in [1], was called the Inverse Set, relative to the Shapley Value. Of course, a second connected problem occurs: for a given vector L, find out some games in the Inverse Set, with the Shapley Value in the Core. How do you solve this problem, for the case of the Shapley Value and the Banzhaf Value is discussed in [2] and [3], and for the Semivalues in [4]. The two cases, efficient and non efficient Semivalues are presented, by introducing also the concept of coalitional rationality in the last case. Now, an interesting new value has been introduced by A.Puente in [5], called the Binomial Semivalue, and we discussed in [6] the two problems above, relative to this value. In an earlier work, [7], we were modeling the gas routing problem as a game theoretic problem, by using the ideas introduced by Kalai/Zemel in [8], and we discussed the Inverse Problem, relative to Binomial Semivalues. In the present paper, the Inverse Problem relative to these values, with Coalitional Rationality, is discussed as follows. In the second section, the model of Gas Routing is presented, by taking a numerical example, where the numbers are taken arbitrarily by the author. The results of the earlier work connected to the Inverse Problem with Coalitional Rationality, relative to the Shapley Value, were applied to the Flow Game in the third section. The results on the Inverse Problem with Coalitional Rationality, relative to the Semivalues, are applied in the fourth section to the Binomial Semivalues of the Game obtained earlier in the Gas Routing, and a solution for the two problems is given in this case. Discussions about some special situations that may occur in connection to the Gas Routing model are carried in the last section.
The set of all games solutions of this problem, introduced and determined in [1], was called the Inverse Set, relative to the Shapley Value. Of course, a second connected problem occurs: for a given vector L, find out some games in the Inverse Set, with the Shapley Value in the Core. How do you solve this problem, for the case of the Shapley Value and the Banzhaf Value is discussed in [2] and [3], and for the Semivalues in [4]. The two cases, efficient and non efficient Semivalues are presented, by introducing also the concept of coalitional rationality in the last case. Now, an interesting new value has been introduced by A.Puente in [5], called the Binomial Semivalue, and we discussed in [6] the two problems above, relative to this value. In an earlier work, [7], we were modeling the gas routing problem as a game theoretic problem, by using the ideas introduced by Kalai/Zemel in [8], and we discussed the Inverse Problem, relative to Binomial Semivalues. In the present paper, the Inverse Problem relative to these values, with Coalitional Rationality, is discussed as follows. In the second section, the model of Gas Routing is presented, by taking a numerical example, where the numbers are taken arbitrarily by the author. The results of the earlier work connected to the Inverse Problem with Coalitional Rationality, relative to the Shapley Value, were applied to the Flow Game in the third section. The results on the Inverse Problem with Coalitional Rationality, relative to the Semivalues, are applied in the fourth section to the Binomial Semivalues of the Game obtained earlier in the Gas Routing, and a solution for the two problems is given in this case. Discussions about some special situations that may occur in connection to the Gas Routing model are carried in the last section.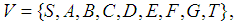 where S is a unique source, T is a unique sink, then
where S is a unique source, T is a unique sink, then 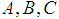 are the drilling vertices, and the three companies denoted by
are the drilling vertices, and the three companies denoted by 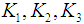 own the sets of ducts
own the sets of ducts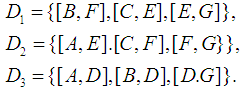 The capacities of the ducts are given by the matrix
The capacities of the ducts are given by the matrix in which the rows for G and T, as well as the columns for S and T, were omitted being almost empty, except
in which the rows for G and T, as well as the columns for S and T, were omitted being almost empty, except 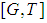 a public duct with capacity 25, used for entering the depot. Of course, in general there may be several public ducts. The capacities of the auxiliary ducts
a public duct with capacity 25, used for entering the depot. Of course, in general there may be several public ducts. The capacities of the auxiliary ducts 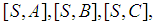 are derived from the number of units of gas obtained per time unit by drilling, while the companies are choosing the overall routing by cooperation. The data were arbitrarily taken by the author. The Flow Game associated to various groups of cooperating players, following the Kalai/Zemel paper [8], who introduced the concept, is the cooperative TU game
are derived from the number of units of gas obtained per time unit by drilling, while the companies are choosing the overall routing by cooperation. The data were arbitrarily taken by the author. The Flow Game associated to various groups of cooperating players, following the Kalai/Zemel paper [8], who introduced the concept, is the cooperative TU game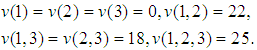

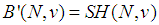 efficient, that is not in the Core. Then, we used the Inverse Problem for Semivalues, the problem we introduced and solved earlier (Dragan, [4]). In the efficient case, we stated the problem as follows: given the vector L, find out the set of all games with the same set N, of players for which we have
efficient, that is not in the Core. Then, we used the Inverse Problem for Semivalues, the problem we introduced and solved earlier (Dragan, [4]). In the efficient case, we stated the problem as follows: given the vector L, find out the set of all games with the same set N, of players for which we have 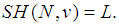 This set was called the Inverse Set, relative to the Shapley Value, and it was given by
This set was called the Inverse Set, relative to the Shapley Value, and it was given by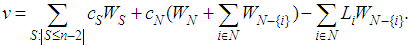
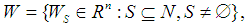 where for all coalitions
where for all coalitions 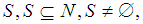 we have
we have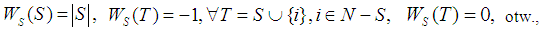
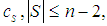 and
and 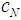 . Now, we want to get a Semivalue which is a Coalitional rational value. In the Inverse Set, we considered the family of games called the almost null family, obtained for all
. Now, we want to get a Semivalue which is a Coalitional rational value. In the Inverse Set, we considered the family of games called the almost null family, obtained for all 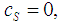 while we kept only the unique parameter
while we kept only the unique parameter 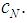 Then, we imposed the condition that the games belong to the Core, from which we got the inequality
Then, we imposed the condition that the games belong to the Core, from which we got the inequality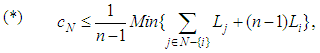 Now, if we take the last parameter to satisfy the inequality and write component wise the almost null family, we get a game with the previously given Shapley Value, that has the value in the Core. For example, in our flow game, associated with the gas routing problem, the inequality (*) is
Now, if we take the last parameter to satisfy the inequality and write component wise the almost null family, we get a game with the previously given Shapley Value, that has the value in the Core. For example, in our flow game, associated with the gas routing problem, the inequality (*) is 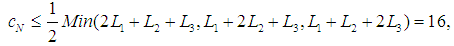
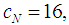 we obtain the game solution
we obtain the game solution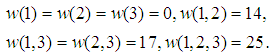
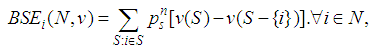
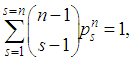
 from the recursive formula
from the recursive formula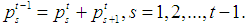
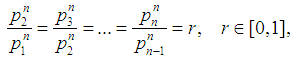
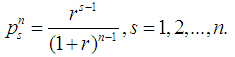
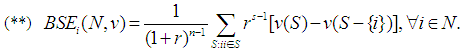 For the Flow Game, shown in the previous section, if we use
For the Flow Game, shown in the previous section, if we use 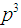 derived from (11), this formula (**) and the characteristic function (2), we get the Binomial Semivalue of this game:
derived from (11), this formula (**) and the characteristic function (2), we get the Binomial Semivalue of this game: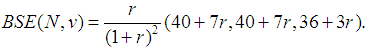
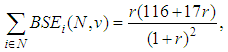
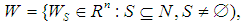
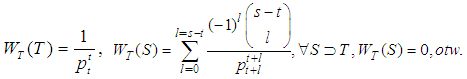
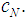 Further, it occurs the fact that, in general, for any value of the parameter
Further, it occurs the fact that, in general, for any value of the parameter  , in terms of r, the games
, in terms of r, the games  in this family have the Binomial Semivalue the same as the previous one, but this is not efficient, in general; hence, it does not belong to the Core. Therefore, as shown in [6], we shall consider the so called Power Game
in this family have the Binomial Semivalue the same as the previous one, but this is not efficient, in general; hence, it does not belong to the Core. Therefore, as shown in [6], we shall consider the so called Power Game 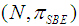 for the games in the almost null family denoted with
for the games in the almost null family denoted with 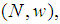 by using for all subgames
by using for all subgames 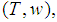 the definition
the definition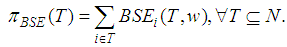
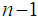 . The games in the almost null family are offered by the expansion
. The games in the almost null family are offered by the expansion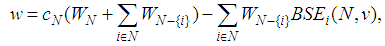
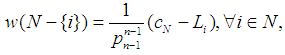
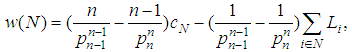
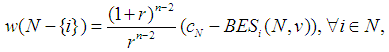
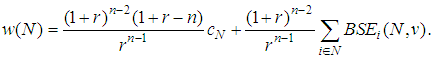
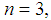 we obtain the family of games
we obtain the family of games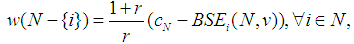
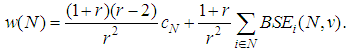
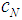 , which will be a function of r, selected such that the Binomial Semivalue is coalitional rational, and this will be done in the next section.
, which will be a function of r, selected such that the Binomial Semivalue is coalitional rational, and this will be done in the next section.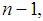 for the games in the Inverse Set. Otherwise, first we should compute the games in the Inverse Set, then
for the games in the Inverse Set. Otherwise, first we should compute the games in the Inverse Set, then 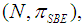 the Power Game of the games from the almost null family
the Power Game of the games from the almost null family 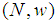 shown in the previous section. We use the definition (16), in which the coalitions T have the size
shown in the previous section. We use the definition (16), in which the coalitions T have the size 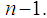 The worth of coalitions of size
The worth of coalitions of size 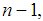 in the Power Game, derived from (16), based upon (22) are
in the Power Game, derived from (16), based upon (22) are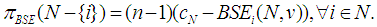
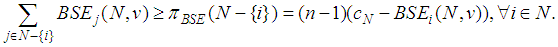
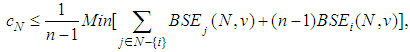
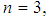 we get:
we get: 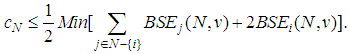
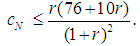
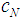 is the potential of the game, let us choose for the parameter, the highest value satisfying (28). A simple computation gives many solutions for our problem, in the Inverse Set, in fact the family of almost null games. We obtain the games:
is the potential of the game, let us choose for the parameter, the highest value satisfying (28). A simple computation gives many solutions for our problem, in the Inverse Set, in fact the family of almost null games. We obtain the games: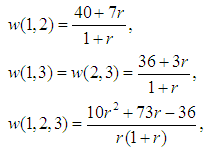
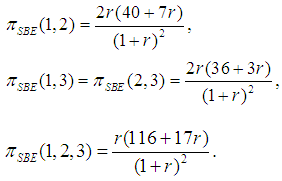
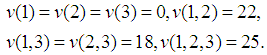
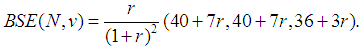
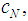 the parameter of the games in the almost null family, namely the highest value possible, and we computed the solution game for the given Flow Game associated to the gas routing problem:
the parameter of the games in the almost null family, namely the highest value possible, and we computed the solution game for the given Flow Game associated to the gas routing problem: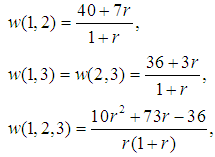
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML