-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2018; 7(1): 1-6
doi:10.5923/j.jgt.20180701.01

Two Dimensional Hotelling Model with Dirichlet Boundary Condition
Yunus Emre Ozcan1, Bahriye Karaca2, Veysel Ulusoy3
1Department of International Finance, Yeditepe University, Istanbul, Turkey
2Faculty of Economics and Administrative Sciences, Gelisim University, Istanbul, Turkey
3Faculty of Applied Sciences, Yeditepe University, Istanbul, Turkey
Correspondence to: Yunus Emre Ozcan, Department of International Finance, Yeditepe University, Istanbul, Turkey.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper examines the location equilibrium in spatial competition framework with two dimensional spaces inside a unit disk. We drive the general conditions for location function under the indirect utility function of consumers. We found the unique solution of symmetric location problem with Dirichlet boundary condition in complex plane for a pin point.
Keywords: Spatial Competition, Location Choice, Game Theory
Cite this paper: Yunus Emre Ozcan, Bahriye Karaca, Veysel Ulusoy, Two Dimensional Hotelling Model with Dirichlet Boundary Condition, Journal of Game Theory, Vol. 7 No. 1, 2018, pp. 1-6. doi: 10.5923/j.jgt.20180701.01.
Article Outline
1. Introduction
- The analysis of firms’ competition is one of the main aspects of the economic studies. The problem of firms’ competition has a vast literature and the classical concepts such as perfect competition, price equilibrium and oligopoly have already been introduced. One of the important concepts of competition literature, Bertrand paradox1 states that firms earn zero profit due to price reduction by its’ competitors to attract more customers in the market until the marginal cost of product equals the product price for each firm in the market. Product differentiation, transportation cost, non-perfect competition concepts relax this assumption. Location game is the main focused area of this paper; this concept was first introduced to economic literature by [10]. Hotelling model analyzes the behavior of two sellers of a homogenous product who chooses price and location in a bounded one dimensional marketplace where consumers are distributed on line length l and product price is associated with transportation cost which is proportional to the distance between the consumers and firms [10]. In this setting, the optimal location choice of the firms is the main driver of the spatial competition amongst the firms. In this original article; it has been found that competing firms tend to be located close to each other and price equilibrium does not exist unless one of the competing firms chooses quadratic transportation cost rather than linear transportation cost. Linear transportation cost could not provide an existence of price equilibrium for each possible pair of locations in one dimensional market place [7]. In [8], Hotelling model was generalized to find locational existence equilibrium over a disk for spatial competition.2 Economides [8] showed that regions of existence of equilibrium in the price game for intermediate product differentiation with quadratic and linear transportation cost.3Tabuchi [18] has demonstrated that competing two firms locate at the midpoint of one side opposite to each other in rectangular two dimensional market spaces. On the other hand, he stated that firms tend to minimize their distance in one dimension market place. In the case of a hypercube market place, Irmen and Thisse [11] have shown that two firms to differentiate their products in one dimension only (see e.g [2]). Feldin [9] has shown that two firms location on the perimeter of the disk and firms located themselves exactly opposite of each other. In case of different shapes of the market without the spatial restriction, firms can locate the outside of the market areas (see e.g [17]).Our methodological framework allows us to examine firm’s location problem inside of a unit disk. We try to solve competing firm’s symmetric optimal location problem in order to find out existence of Nash equilibrium on a location game. Main contribution of the article to existing literature is to set the Dirichlet boundary conditions for two-dimensional market place in terms of optimal location problem for spatial competition framework. Consumers are uniformly distributed inside of a unit disc rather than on an interval. Consumers have the same demand, preferences and income. Transportation cost is homogenous and increases with distance. Consumers’ objective is to have maximum utility. We present the indirect consumer’s utility function by using complex analysis and having producers distributed inside the unit disc.In the first part of the paper, the necessary material from complex analysis is reviewed. Second part of the paper states the theoretical model and third part of the paper explains symmetric optimal location problem for existence of equilibrium with the boundary conditions.
2. Background
- This section gives insight on the Dirichlet boundary value problems for complex partial differential equations. Basic definitions and concepts from complex analysis are presented.Definition 3.1 [13]: Let
 complex plane, a complex valued function of the variable
complex plane, a complex valued function of the variable 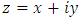 and
and 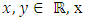 is called the real part of z and is denoted by Rez, y is called imaginary part of z and is denoted by Imz. The complex number
is called the real part of z and is denoted by Rez, y is called imaginary part of z and is denoted by Imz. The complex number 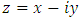 is called the conjugate of z. The extended complex plane is denoted by
is called the conjugate of z. The extended complex plane is denoted by 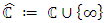 , a domain D in
, a domain D in 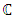 is called regular if it is bounded and its boundary
is called regular if it is bounded and its boundary 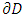 is being a smooth curve.A complex valued function
is being a smooth curve.A complex valued function 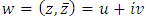 be defined in
be defined in 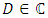 and let
and let 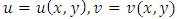 are real valued functions. When u and v are differentiable and w is independent of
are real valued functions. When u and v are differentiable and w is independent of 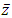 in an open set
in an open set 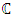 the function w is called analytic in the set.A complex valued function w which is independent of
the function w is called analytic in the set.A complex valued function w which is independent of 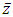 , satisfying the differential equation in an open domain D in C,
, satisfying the differential equation in an open domain D in C, 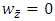 is called analytic function in D.The complex partial differential operator
is called analytic function in D.The complex partial differential operator 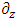 and
and 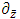 are defined by
are defined by 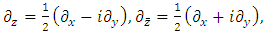
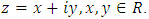 Theorem 3.2 [13] Let w be an analytic function in a simply connected domain
Theorem 3.2 [13] Let w be an analytic function in a simply connected domain 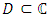 and let
and let 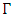 be a simple closed curve
be a simple closed curve 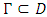 , then
, then 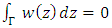 The fundamental tools for solving the boundary value problems for complex partial differential equations are the Gauss theorem and the Cauchy -Pompeiu Representation formula.Theorem 3.3 [3] (Gauss Theorem, complex form) Let
The fundamental tools for solving the boundary value problems for complex partial differential equations are the Gauss theorem and the Cauchy -Pompeiu Representation formula.Theorem 3.3 [3] (Gauss Theorem, complex form) Let 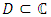 be a regular domain and
be a regular domain and 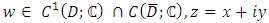 , then
, then 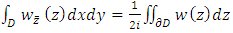 and
and 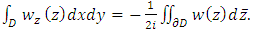 From the Gauss Theorem the Cauchy-Pompeiu Representation can be obtained.Theorem 3.4 [3] (Cauchy- Pompeiu Representation) Let
From the Gauss Theorem the Cauchy-Pompeiu Representation can be obtained.Theorem 3.4 [3] (Cauchy- Pompeiu Representation) Let 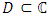 be a regular domain and
be a regular domain and 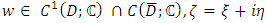 , then
, then 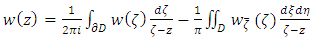 and
and 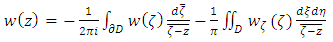
3. Brief description of the Model
- This section gives a brief description of the model described in this paper. We consider a unit disk market4 with two dimensional space in which two competing firms exist and both firms offer identical products in all respects except for the location of availability and firms choose locations inside the unit disk. Consumers are uniformly distributed inside the unit disk. Each consumer demands a single unit of product and faces transportation cost to buy one unit of product. Under these settings, we explore the perfect Nash equilibrium.
4. Model and Its Equilibrium
- By definition spatial market considers equilibrium; none of the competing firms find a combination of location and price that makes one firm more profitable than another. Given by this definition, this market consists of two competing firms; a and b, and the consumers choose between the two and their utility can be expressed as follows;
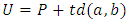 | (1) |
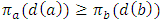 | (2) |
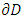 and twice differentiable. Firms are apart from each other at equal and opposite distance from consumers.Proof.We define the location problem as the complex valued function to find optimal interior point in a unit disk. Location of firm a is given by
and twice differentiable. Firms are apart from each other at equal and opposite distance from consumers.Proof.We define the location problem as the complex valued function to find optimal interior point in a unit disk. Location of firm a is given by 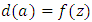 where;
where; 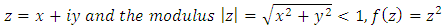 Symmetric solution of the location equilibrium is the complex conjugate of the location
Symmetric solution of the location equilibrium is the complex conjugate of the location 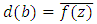 where;
where; 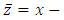
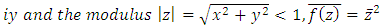 Theorem 5.1 [3]. The Dirichlet problem for the inhomogeneous Bitsadze equation in the unit disc
Theorem 5.1 [3]. The Dirichlet problem for the inhomogeneous Bitsadze equation in the unit disc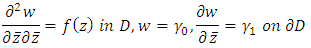 for
for 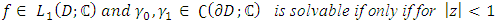
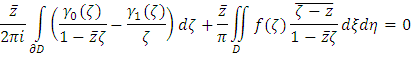 and
and 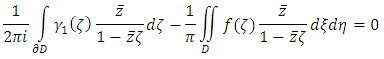 the solution then is uniquely given by the formula
the solution then is uniquely given by the formula 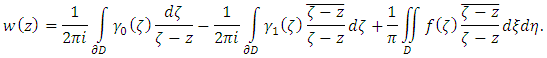 As an application of Theorem 5.1 considering the following boundary value problem
As an application of Theorem 5.1 considering the following boundary value problem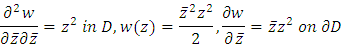 Cauchy-Pompeiu Representation reduces the boundary value problem for differential equation to integral equation in order to prove the existence of uniqueness. The first solvability condition
Cauchy-Pompeiu Representation reduces the boundary value problem for differential equation to integral equation in order to prove the existence of uniqueness. The first solvability condition 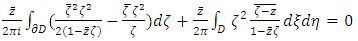 | (3) |
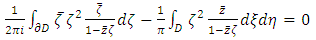 | (4) |
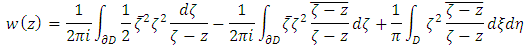 By using the Gauss Theorem, the equation 3 i.e. first solvability condition can be written as
By using the Gauss Theorem, the equation 3 i.e. first solvability condition can be written as 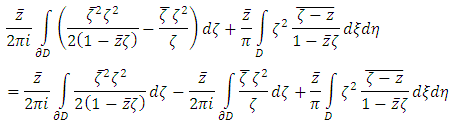 And from the Gauss Theorem it follows that
And from the Gauss Theorem it follows that 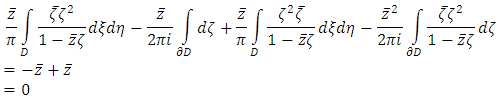 Using Gauss Theorem the second solvability condition can be written as
Using Gauss Theorem the second solvability condition can be written as 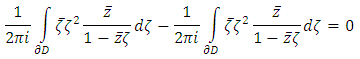 So the solution is uniquely given by the following formula.
So the solution is uniquely given by the following formula.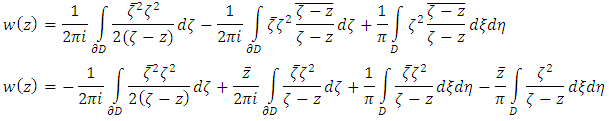 Using Cauchy-Pompeiu Representation formula it follows that
Using Cauchy-Pompeiu Representation formula it follows that 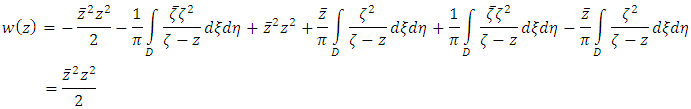 This is the firm
This is the firm 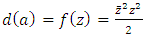 optimal location inside the unit disk given boundary conditions. It is always possible for firm b to increase its profit by moving to the closest location of firm a and cutting its price to just below that of firm a. Therefore stability of equilibrium cannot emerge. We employ same procedure for firm b so that no firm can make a small change in its location and price which generate a larger gross profit than that obtained by its present choice of location and price. At this stage, we try to find optimal location for firm b by using complex conjugate of the location of firm a.Theorem 5.2 [3] The Dirichlet problem for complex conjugate of the inhomogeneous Bitsadze equation in unit disk
optimal location inside the unit disk given boundary conditions. It is always possible for firm b to increase its profit by moving to the closest location of firm a and cutting its price to just below that of firm a. Therefore stability of equilibrium cannot emerge. We employ same procedure for firm b so that no firm can make a small change in its location and price which generate a larger gross profit than that obtained by its present choice of location and price. At this stage, we try to find optimal location for firm b by using complex conjugate of the location of firm a.Theorem 5.2 [3] The Dirichlet problem for complex conjugate of the inhomogeneous Bitsadze equation in unit disk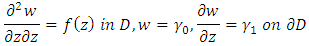 for
for 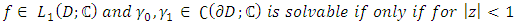
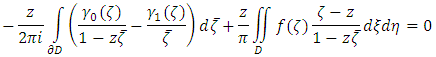 and
and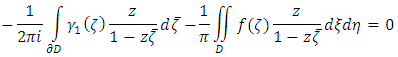 the solution then is uniquely given by the formula
the solution then is uniquely given by the formula 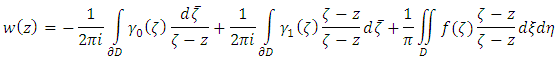 As an application of Theorem 5.2
As an application of Theorem 5.2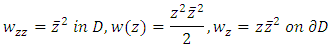 The first solvability condition
The first solvability condition 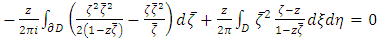 | (5) |
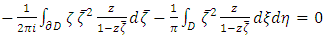 | (6) |
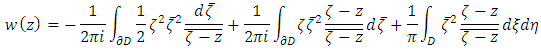 By using the Gauss Theorem, the equation 5 i.e. first solvability condition can be written as
By using the Gauss Theorem, the equation 5 i.e. first solvability condition can be written as 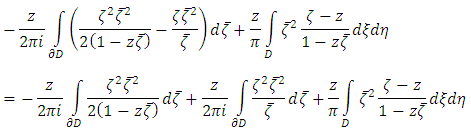 And from the Gauss Theorem it follows that
And from the Gauss Theorem it follows that 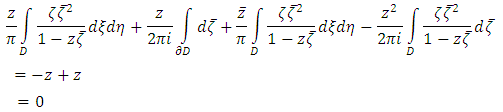 Using Gauss Theorem the second solvability condition can be written as
Using Gauss Theorem the second solvability condition can be written as 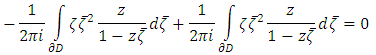 So the solution is uniquely given by the following formula
So the solution is uniquely given by the following formula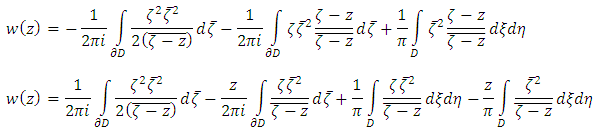 Using Cauchy-Pompeiu Representation formula it follows that
Using Cauchy-Pompeiu Representation formula it follows that 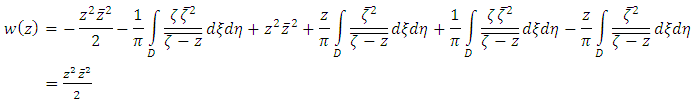 Complex conjugate location of firm b is
Complex conjugate location of firm b is 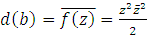 , under the Dirichlet boundary condition in unit disk; we find both firms optimal location to generate equilibrium.
, under the Dirichlet boundary condition in unit disk; we find both firms optimal location to generate equilibrium. 5. Conclusions
- The spatial economics covers location theory, spatial competition and regional and urban economics. The fundamental problem of the spatial economics is to determine allocation of resources over space and the location of economic activity. The choice of location of economic activity directly impacts the economic growth and international trade. In this paper, we analyzed the two-dimensional unit disk market with spatial restriction. We provide location function for the competing firms based on the market range framework in generalized Hotelling model in complex plane with boundary condition. We find the firm locations in symmetric opposite points in the plane. On the contrary to the previous studies, we consider only location game in our model to satisfy spatial restriction of the two-dimensional unit disk market. The model could be extended with inclusion of price game for further research.
Notes
- 1. See [4]2. Economides [8] used to euclidian distance metrics to find existence equilibrium.3. Salop [16] intoduces cicular model on a circle with location equilibra that place firms equidistantly.4. A market place represented as a complex space5. It can be treated as a payoff function of firms
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML