Madhumidha K.1, Vijayarangan N.2, Padmanabhan K.2, Satish B.2
1TCS Intern and Student of BE (CSE), Sona College of Technology, Salem, India
2TTH Innovation Lab, Tata Consultancy Services Ltd (TCS), Chennai, India
Correspondence to: Madhumidha K., TCS Intern and Student of BE (CSE), Sona College of Technology, Salem, India.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The fundamental concept of Nash equilibrium is that any player in a game cannot unilaterally change his/her behaviour(s) to obtain higher payoff. If players get an equal payoff in a game or repeated games, then Nash fails in those scenarios. This paper provides insights on transforming the computed payoffs to a robust shape (Pareto optimality) using PTFT (Probabilistic Tit-for-Tat) strategy. We have applied the derived results to Braess's paradox that could fetch an optimal network path by removing shortest path through the benefits of using PTFT strategy. Further, PTFT can be applied to industrial cases such as duopoly market analysis and legal battle of two firms. It is proved that Nash equilibrium does not yield an optimal solution for repeated games using various case studies.
Keywords:
Probabilistic tit-for-tat strategy, Repeated games, Nash equilibrium, Payoff matrix
Cite this paper: Madhumidha K., Vijayarangan N., Padmanabhan K., Satish B., Probabilistic Tit-for-Tat Strategy versus Nash Equilibrium for Infinitely Repeated Games with Industrial Applications, Journal of Game Theory, Vol. 6 No. 3, 2017, pp. 53-61. doi: 10.5923/j.jgt.20170603.01.
1. Introduction
In this paper, we have proved how PTFT strategy is more optimal than Nash equilibrium which is considered to be the optimal strategy for players involved in infinitely repeated games. The problem in Nash equilibrium is sometimes the game does not provide conclusive results when multiple solutions of Nash equilibria are found. The tit-for-tat strategy is not optimal when the noise (the players occasionally deviate from their behavioural rules, for instance, mistakes and misconception [4]) exists in the system. But PTFT strategy solves the noise problem of the original tit-for-tat strategy using the cost of an arbitrary small λ and δ values [7] (here λ is small positive number less than 1 and δ is the probability value chosen by the player). In the network traffic pattern, if each driver (player) decides to take the path that consumes minimum time then it results in congested traffic and slows the optimal commutes. By applying Nash equilibrium, there are no benefits for any driver to change their routes. Instead of Nash, PTFT strategy should be applied so that each driver could improve their strategies shown here. While engaging PTFT strategy in repeated games, we obtain various game scenarios given to players who may do a better decision analysis. Hence one can predict a player getting maximum payoff through this invention.
2. Background
Even though Nash equilibrium is simple in appearance but it is a complex method for the analysis of non-cooperative games. In a traffic network, each driver (player) always prefers to use Nash equilibrium when the strategy of selecting the route with minimum travel time proceeds into [1]. However, Nash equilibrium is not always robust and their fragility can cause the entire game to become ill-defined or lead to game failure [5]. To overcome these difficulties, PTFT strategy is applied in order to improve payoff of players involved in infinitely repeated games. For instance, let us have a game of matching pennies. Then, there is no pure equilibrium exists so that mixed strategies should be included in the game. In this paper, we have shown that PTFT strategy is applicable in an infinite game when non-existence of equilibria. From [7], we have a model of PTFT strategy of 2x2 game shown in the following table:Table 1. Transition matrix t for 2x2 game
 |
| |
|
Let row vector π denote the probabilities of combinations (strategies that are available for players) and it is independent of δ. Then π satisfies π = πT, where T is a transition matrix.The initial set of vectors for 2x2 game can be written as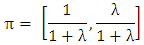 | (1) |
Next, we have a model of PTFT strategy for 4x4 game shown in the following table:Table 2. Transition matrix t for 4x4 game
 |
| |
|
For 4x4 game, the initial set of vectors can be written as 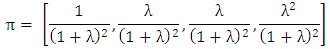 | (2) |
Let the first column of π denote the probability that players play CC [7]. In this paper, we have derived a generalized way for creating initial set of vectors for 2nx2n repeated games (n ≥ 1). Hence, players in a game can choose strategies with a high probability to gain an optimal outcome (Pareto optimality).
3. Innovative Results
Assume that Nash equilibrium or pure equilibrium fails in infinitely repeated games. When we apply PTFT strategy to the game, it provides an optimal outcome shown for each game with the probability of choosing the best strategy for each player involved in the game. In this paper consider PTFT strategy is applied to 8x8, 16x16 repeated games and so on. Here the following table represents possible strategies available for players and the output will be one of 8 combinations of CCC, CCD, CDC, DCC, DCD, DDC, CCD and DDD for 8x8 repeated games.Table 3. Transition matrix t for 8x8 game
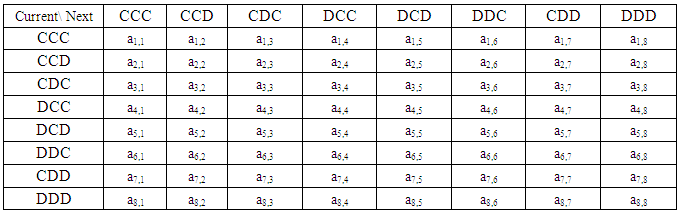 |
| |
|
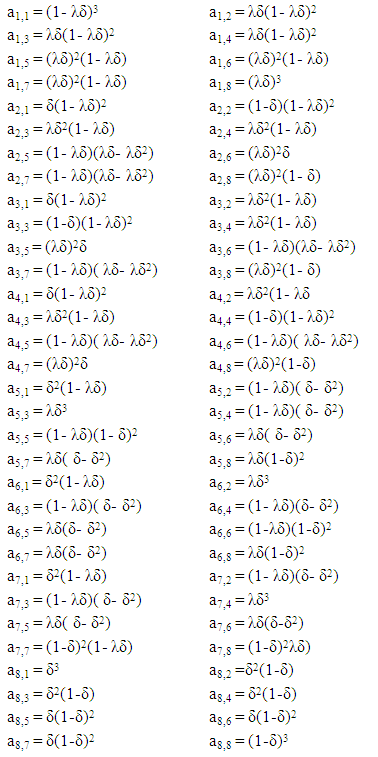 The initial set of vectors for 8x8 game will be
The initial set of vectors for 8x8 game will be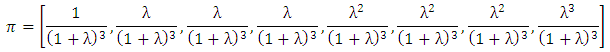 | (3) |
Next, PTFT strategy is applied to 16x16 repeated games whose payoff matrix is represented in table 4.Table 4. Transition matrix t for 16x16 game
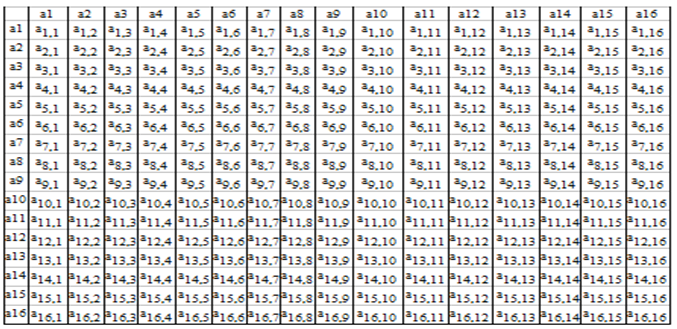 |
| |
|
From table 4, a1 - CCCC a2 - CCCD
a2 - CCCD a3 - CCDC
a3 - CCDC a4 - CDCC
a4 - CDCC a5 - DCCC
a5 - DCCC a6 - CCDD
a6 - CCDD a7 - CDDC
a7 - CDDC a8 – CDCD
a8 – CDCD a9 - DCDC
a9 - DCDC a10 - DDCC
a10 - DDCC a11 - DCCD
a11 - DCCD a12 – CDDD
a12 – CDDD a13 - DDCD
a13 - DDCD a14 - DCDD
a14 - DCDD a15 - DDDC
a15 - DDDC a16 – DDDD
a16 – DDDD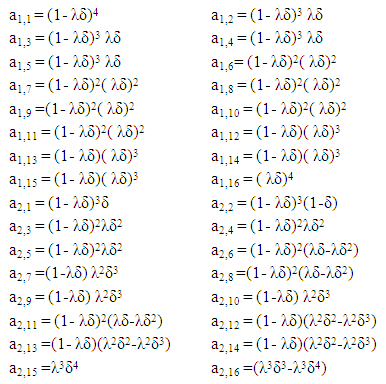
 The initial set of vectors for 16×16 games will be
The initial set of vectors for 16×16 games will be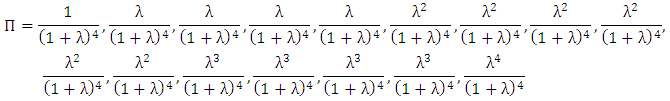 | (4) |
The generalization way of initial set of vectors for 2nx2n repeated games will be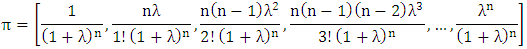 | (5) |
From Equation (5), the set of elements can be multiplied by the factors 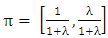 then we have 2n+1 elements of π as follows:
then we have 2n+1 elements of π as follows: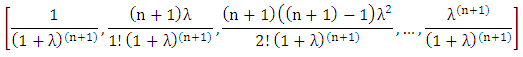 | (6) |
By mathematical induction method, we have proved that PTFT strategy is true for any n.
4. Generalization of PTFT over Nash Equilibrium
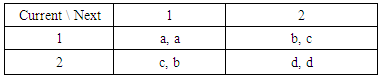
When Nash equilibrium is applied, players do not get any incentives to deviate from their equilibrium strategies [2]. Inducible games of 2x2 can be stabilized via PTFT [8]. In our research work, PTFT strategy is applied to 2nx2n repeated games, players get benefited with an improved payoff. For instance, the general payoff matrix for 2x2 game is given in the following table:Table 5. Payoff matrix for 2x2 game
 |
| |
|
Here 1 and 2 are the strategies available to players. From [7], PTFT strategy for 2x2 game is shown in below table.Table 6. Transition matrix t for 2x2 game
 |
| |
|
Here, δ is a small positive number and λ is a non-negative number less than 1. By matrix multiplication of initial set of vectors of 2x2 game with PTFT transition matrix of 2x2 game from table 6, we prove that PTFT is optimal by adding the initial set of vectors to be 1 (the probability value always lies in the range of 0 to 1).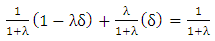 | (7) |
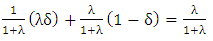 | (8) |
Thus, by matrix multiplication we get the initial set of vectors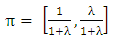 | (9) |
By summing Equation (9), we get the probability value.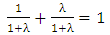 | (10) |
Similarly, we can prove for repeated games of 4x4 by performing matrix multiplication of initial set of vectors with PTFT payoff matrix as follows: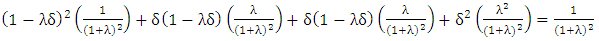 | (11) |
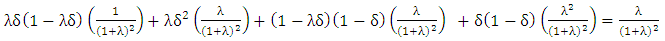 | (12) |
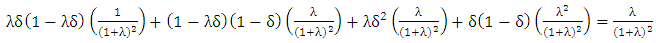 | (13) |
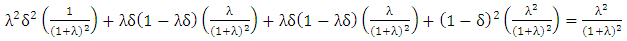 | (14) |
By summing Equations (11) to (14) we get,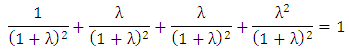 | (15) |
For any n (where n ≥ 1), we conclude for repeated games of 2nx2n, PTFT strategy gives the optimal solution. Hence, by generalization of PTFT we have,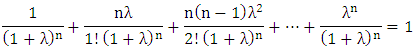 | (16) |
5. Implementation Results
To compute the expected payoff of a game using PTFT strategy, we derive ε–optimal strategy for 8x8 game as follows.Let P, S, T, R be the scalar values of initial set of vectors belonging to 8x8 game. The expected payoff of a PTFT player against another for 8x8 game is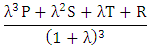 | (17) |
To find the discriminant of 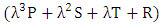 we use,
we use,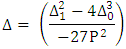 | (18) |
Where  and
and 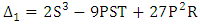 We need three real solutions of λ for which
We need three real solutions of λ for which 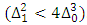 .For 8x8 game, we have conditions to obtain optimal strategy which is given by
.For 8x8 game, we have conditions to obtain optimal strategy which is given by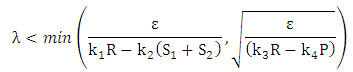 | (19) |
where 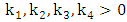 .For 16x16 game, the expected payoff of PTFT is given by
.For 16x16 game, the expected payoff of PTFT is given by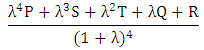 | (20) |
where P, S, Q, T, R are the scalar values of initial set of vectors belonging to 16x16 game. To find the real roots of 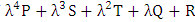 , we have
, we have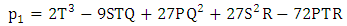 | (21) |
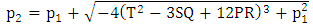 | (22) |
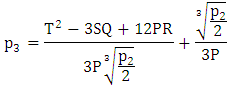 | (23) |
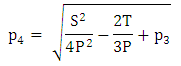 | (24) |
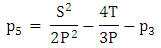 | (25) |
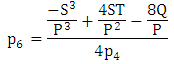 | (26) |
Also, 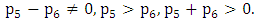 The possible solutions are,
The possible solutions are,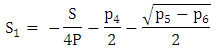 | (27) |
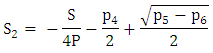 | (28) |
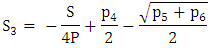 | (29) |
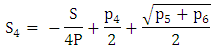 | (30) |
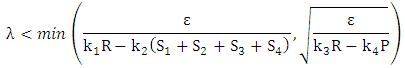 | (31) |
Through implementation, we derive that πcc…c = 1 as λ tends to 0. This shows that the game has achieved Pareto optimality. The relation between πcc…c with λ for 2nx2n repeated game is given in the below graph.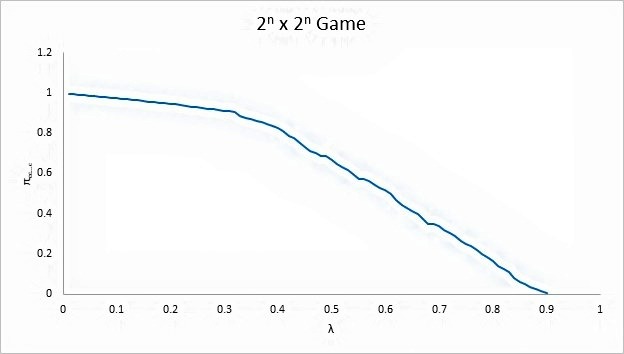 | Figure 1. 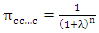 |
6. Industrial Applications
6.1. Case Study of Coordination Game
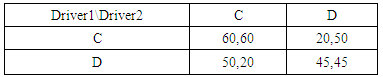
Consider a driver (player) driving on a road against an incoming car, who has to choose either to Cooperate (C) or to Defect (D) using the road network.Table 7. Payoff matrix of coordination game
 |
| |
|
If both drivers cooperate, each will get a payoff of 60; if both defect, each will get a payoff of 45; and if one cooperates and the other defects then the cooperating driver will get a payoff of 20 and the defecting driver will get a payoff of 50 and vice versa. There are two Nash equilibria found in this game (60,60) and (45,45), here the drivers cannot improve their payoffs using Nash equilibrium. This is a complexity that is found in Nash equilibrium. When applying PTFT strategy in this game, we choose λ = 0.25 and δ = 0.85 since π is independent of δ, payoff of both players can be improved and the probability of choosing the strategy (decision making shown in table 8) may be obtained.Table 8. Probabilistic decision for 2x2 game
 |
| |
|
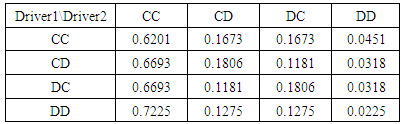
Continuing the game, we move to the next level of 4x4. Then, the possible outcome of players is one of the four combinations of CC, CD, DC and DD shown below.Table 9. Probabilistic decision for 4x4 game
 |
| |
|
Continuing the game, we move to the next level of 8x8. Then, the possible outcome of players is one of the eight combinations of CCC, CCD, CDC, DCC, DCD, DDC, CDD, DDD shown below.Table 10. Probabilistic decision for 8x8 game
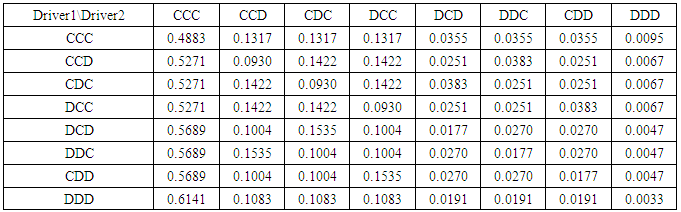 |
| |
|
However, the payoffs of Nash equilibrium are always same in coordination game. We have tested and verified the improved efficiency of the game after applying PTFT strategy.
6.2. Case Study of Braess's Paradox
Consider an airline traffic network where flights should reach destination (END) from source (START). If the path from A-B does not exist (Fig. 2), each flight takes 80 minutes to reach the destination using the network path of START-A-END or START-B-END. Even though the given network paths are congested or due to bad weather they will take a maximum time of 90 minutes. If all flights cooperate to take the shortest route (A-B), they may take 120 minutes (assume that there is only one shortest route available). 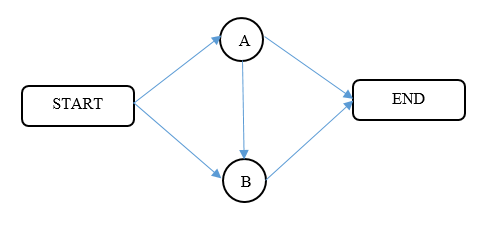 | Figure 2. Airline network graph |
The payoff matrix for flights to reach destination is shown below.Table 11. Payoff matrix of two flights
 |
| |
|
Here AR-Alternate Route, OR-Original Route of the airline traffic network. If Nash equilibrium is applied then we get (120,120). The outcome is not optimal since it takes 120 minutes. In this situation the flights cannot improve their strategy (using Nash equilibrium), while applying PTFT strategy the overall travel time of all flights gets reduced. If all flights agree not to use A-B network, every flight would benefit by reducing their travel time. However, any single flight will always benefit by taking A-B network, then the socially optimal network path distribution of all flights may not be stable hence Braess's Paradox [1] occurs in this situation. Removing a road (network path) can improve traffic and overall efficiency. After choosing the values of λ = 0.3 and δ = 0.7 we get the probability of choosing the strategies (AR/OR) for 2x2 game.Table 12. Probabilistic decision for 2x2 game
 |
| |
|
Continuing the game we move to the next level of 4x4. Then, the possible outcome of all flights is one of the following strategies as shown below.Table 13. Probabilistic decision for 4x4 game
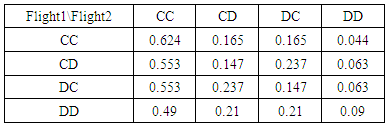 |
| |
|
Continuing the game, we move to the next level of 8x8. Then, the possible outcome of all flights is one of the following strategies is shown below.Table 14. Probabilistic decision for 8x8 game
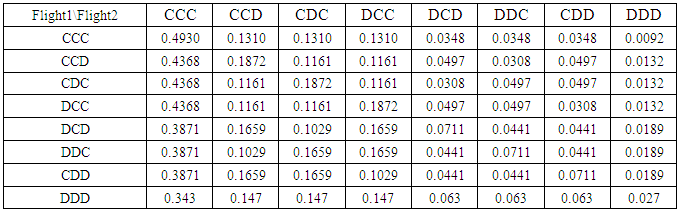 |
| |
|
6.3. Case Study of Price War
From [9], on August 14, 2012, Liu Dongqiang, the CEO of JINGDONG company, posted a news in Weibo and other senior managers including Suning, Gome responded this Weibo mentioning a new E-Commerce price war started, as Dang, Yixun companies joined this war, which finally evolved into a free-for-all of the entire domestic electricity industry's war. In recent years, the development of home appliance industry has been good and then a price war often occurs among air conditioners, washing machines, microwave ovens and other commodities. The two online retailers JINGDONG and SUNING set prices for their products. The payoff matrix of two firms (JINGDONG and SUNING) is shown below.Table 15. Payoff matrix of two firms
 |
| |
|
Here HP-High Price and LP-Low Price are the strategies available for two firms (players). In this case study, there exists Nash equilibrium (LP, LP). The pair (HP, HP) is better in the sense of Pareto efficiency. If the decisions of two online retailers are rational, then there won’t be any price war between them [9]. In our research work, we apply PTFT strategy to this case study by choosing the values of λ = 0.1 and δ = 0.98, the efficiency of two online retailers gets increased. The probability of choosing the strategy (HP/LP) is shown below.Table 16. Probabilistic decision for 2x2 game
 |
| |
|
Continuing the game, we move to the next level of 4x4. Then, the possible outcome of players is one of the following strategies as shown below.Table 17. Probabilistic decision for 4x4 game
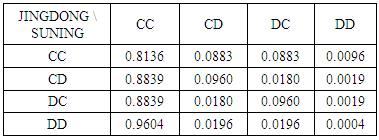 |
| |
|
Continuing the game we move to the next level of 8x8. Then, the possible outcome of players is one of the following strategies as shown below.Table 18. Probabilistic decision for 8x8 game
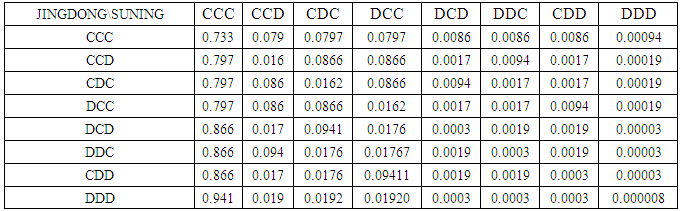 |
| |
|
Similarly, the probability for choosing the strategy can be obtained for 2nx2n repeated games. When we apply PTFT strategy to the game of price war, it gives better outcome for repeated games. Hence, we prove that PTFT strategy is optimal to Nash equilibrium.
6.4. Case Study of Legal Battle
The cellular company Samsung ran into legal issues around 2012. In order to compete Apple’s market, Samsung launched Galaxy with some features resembling iPhone facilities. Apple had patented for some features in iPhone hardware but the same feature was implemented in Samsung’s android phone. Apple Company filed a suit against Samsung, so this legal battle can be viewed as a game. From payoff matrix, F – File a lawsuit and DF – Does not file a lawsuit. Table 19. Payoff matrix of two firms
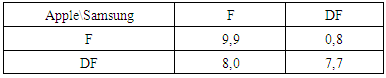 |
| |
|
In this case study if we apply Nash equilibrium, then there exist two solutions of (9,9) and (7,7). The outcome is not optimal for both companies. When we apply PTFT strategy to this game, companies can improve their payoffs. By applying PTFT strategy, we choose λ = 0.15 and δ = 0.65.Table 20. Probabilistic decision for 2x2 game
 |
| |
|
Continuing the game we move to the next level of 4x4. Then, the possible outcome of two firms is one of the following strategies as shown below.Table 21. Probabilistic decision for 4x4 game
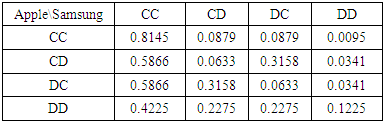 |
| |
|
Continuing the game we move to the next level of 8x8. Then, the possible outcome of two firms is one of the following strategies as shown below.Table 22. Probabilistic decision for 8x8 game
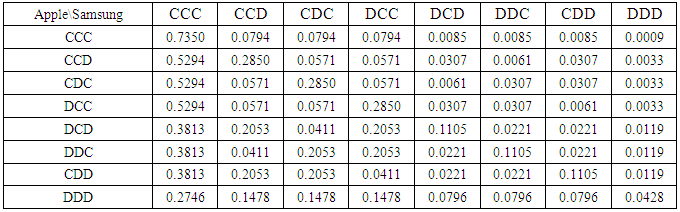 |
| |
|
6.5. Case Study of Duopoly Market Analysis
From [6], Duopoly is a form of oligopoly market having two participants (producers/sellers). The number of competitors is limited to two and their interactions are important because every producer before making decisions on prices and quantities, has to take into account not only the current strategy of the competitor but also forthcoming responsive actions. In duopoly market both firms can coordinate and fix prices of their products. The payoff matrix of two firms is shown below where F – Follow, C – Cheat.Table 23. Payoff matrix of two firms
 |
| |
|
Firms have two strategies either to follow or to cheat the other firm. In this case study, there exists Nash equilibrium (93,93). When Nash equilibrium is applied, both firms get stuck in (C,C) therefore this outcome is not optimal. By applying PTFT strategy in this game, we choose λ = 0.3 and δ = 0.94 and the firms can unilaterally improve their payoffs. Table 24. Probabilistic decision for 2x2 game
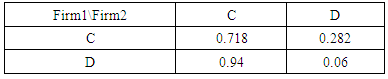 |
| |
|
Continuing the game we move to the next level of 4x4. Then, the possible outcome of two firms is one of the following strategies shown below.Table 25. Probabilistic decision for 4x4 game
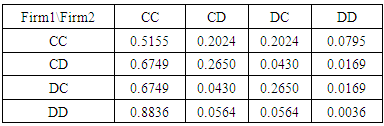 |
| |
|
Continuing the game we move to the next level of 8x8. Then, the possible outcome of two firms is one of the following strategies shown below.Table 26. Probabilistic decision for 8x8 game
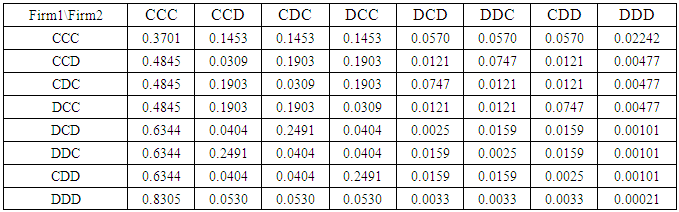 |
| |
|
7. Conclusions
Nash equilibrium is a solution concept in game theory and it does not give an optimal solution for repeated games. The players get stuck in repeated games because they cannot unilaterally change their strategy. PTFT strategy resolves the complexity that arises in Nash equilibrium. We have generalized PTFT strategy results to infinitely repeated games. In this paper, PTFT strategy is applied to various industrial case studies and proved that PTFT strategy is better than Nash equilibrium for repeated games. For each repeated game, we analyze the conditions for ε–optimal strategy.
ACKNOWLEDGEMENTS
We thank Tata Consultancy Service Ltd (TCS) at IITM Research Park, India for carrying out a valuable research project work.
References
| [1] | Brian Skinner, Brad Carlin, “The price of anarchy – on the roads and in football,” The Royal Statistical Society (2013). |
| [2] | F. Munoz-Garcia and D. Toro-Gonzalez, “Pure Strategy Nash Equilibrium and Simultaneous-Move Games with Complete Information,” Strategy and Game Theory, DOI 10.1007/978-3-319- 32963-5_2 (2016). |
| [3] | Gregory Valiant and Tim Roughgarden, “Braess’s Paradox in Large Random Graphs,” University of California, Berkeley and Stanford, CA 94305 (2008). |
| [4] | Michael Mas, Heinrich H. Nax, “A behavioral study of “noise” in coordination games,” Volume 162 (2016). |
| [5] | Philip Vos Fellman, “The Nash Equilibrium Revisited: Chaos and Complexity Hidden in Simplicity,” Southern New Hampshire University Manchester, NH. |
| [6] | Romualdas Ginevičius & Algirdas Krivka (2008) Application of game theory for duopoly market analysis, Journal of Business Economics and Management, 9:3, 207-217. |
| [7] | Shenghuo Zhu “Learning to Cooperate,” University of Rochester Rochester, New York (2003). |
| [8] | Steven J. Brams and D. Marc Kilgour, “Inducible Games: Using Titfor-Tat to Stabilize Outcomes,” New York University, NY 10012 USA and Wilfrid Laurier University Waterloo, Ontario N2L 3C5 CANADA (2012). |
| [9] | Yue Hu, Manzhen Tang, “Game Theory Analysis of E-Commerce’s Price War,” Jinan University Management School, Guangzhou, China (2014). |


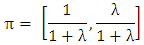
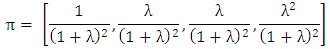
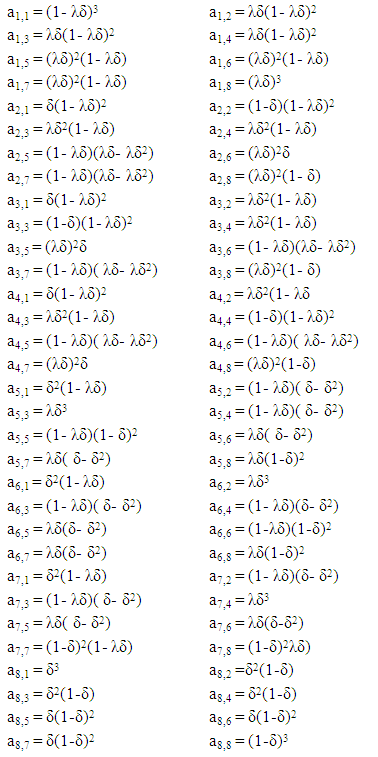 The initial set of vectors for 8x8 game will be
The initial set of vectors for 8x8 game will be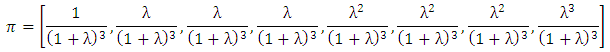
 a2 - CCCD
a2 - CCCD a3 - CCDC
a3 - CCDC a4 - CDCC
a4 - CDCC a5 - DCCC
a5 - DCCC a6 - CCDD
a6 - CCDD a7 - CDDC
a7 - CDDC a8 – CDCD
a8 – CDCD a9 - DCDC
a9 - DCDC a10 - DDCC
a10 - DDCC a11 - DCCD
a11 - DCCD a12 – CDDD
a12 – CDDD a13 - DDCD
a13 - DDCD a14 - DCDD
a14 - DCDD a15 - DDDC
a15 - DDDC a16 – DDDD
a16 – DDDD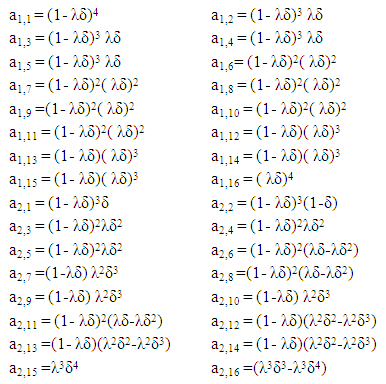
 The initial set of vectors for 16×16 games will be
The initial set of vectors for 16×16 games will be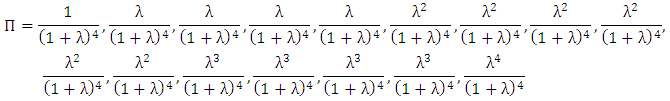
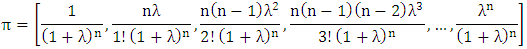
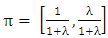 then we have 2n+1 elements of π as follows:
then we have 2n+1 elements of π as follows: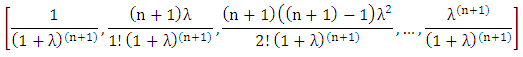
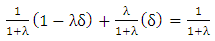
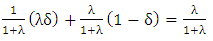
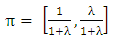
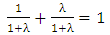
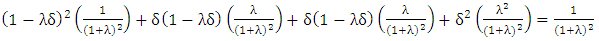
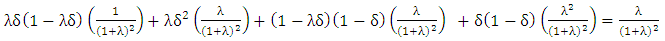
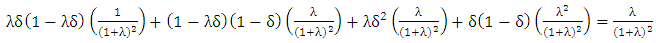
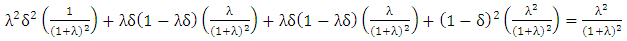
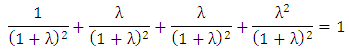
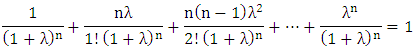
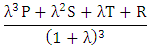
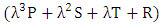 we use,
we use,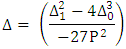
 and
and 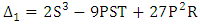 We need three real solutions of λ for which
We need three real solutions of λ for which 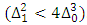 .For 8x8 game, we have conditions to obtain optimal strategy which is given by
.For 8x8 game, we have conditions to obtain optimal strategy which is given by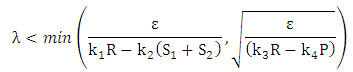
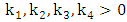 .For 16x16 game, the expected payoff of PTFT is given by
.For 16x16 game, the expected payoff of PTFT is given by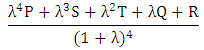
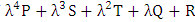 , we have
, we have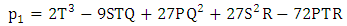
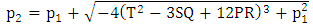
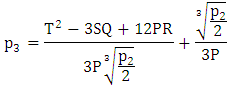
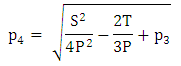
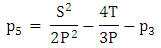
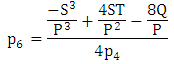
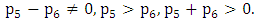 The possible solutions are,
The possible solutions are,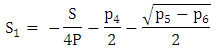
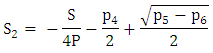
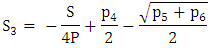
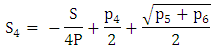
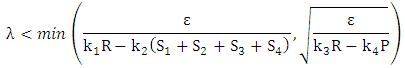

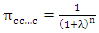

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
























