-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2017; 6(2): 43-51
doi:10.5923/j.jgt.20170602.03

The Pre-nucleolus for Fuzzy Cooperative Games
Yeremia Maroutian
1710, Prospect Ave. Cleveland, Oh. 44115
Correspondence to: Yeremia Maroutian , 1710, Prospect Ave. Cleveland, Oh. 44115.
| Email: |  |
Copyright © 2017 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper invented by D. Schmeidler (1969) for characteristic function games concept of nucleolus has been extended on fuzzy cooperative games. The fuzzy pre-nucleolus defined by a new way. On the set of classical cooperative games proved its coincidence with the already existed one. For a class of fuzzy games the pre-nucleolus exists and unique. The process of finding of pre-nucleolus illustrated on an example of a fuzzy game.
Keywords: Fuzzy cooperative games, Fuzzy coalition, Fuzzy pre-nucleolus
Cite this paper: Yeremia Maroutian , The Pre-nucleolus for Fuzzy Cooperative Games, Journal of Game Theory, Vol. 6 No. 2, 2017, pp. 43-51. doi: 10.5923/j.jgt.20170602.03.
Article Outline
1. Introduction
- Let N= {1, 2… n} be the set of all players. A fuzzy coalition is an n-dimensional vector
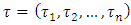 with
with 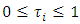 for each
for each 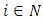 . A cooperative fuzzy game with the players set N is a pair (T, v), where
. A cooperative fuzzy game with the players set N is a pair (T, v), where 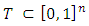 is the set of all fuzzy coalitions and v is the characteristic function of that game which maps a real number to each fuzzy coalition.Cooperative fuzzy games reflect situations in which for players allowed to take part in a coalition with participation levels that may vary from non-cooperation to full cooperation. The obtained reward in this type of games defines depending on the level of cooperation. Participation levels at which players involved in cooperation gets described by fuzzy coalitions. Aubin (1981) has been explaining use of fuzzy coalitions by following way when he first introduced them in game theory. Every player can choose his level of participation in a coalition instead of whether to participate in it or not. As an example in favor of that approach can be considered case, when individual players reluctant to invest all of the available resources in enterprise where that coalition involved. For fuzzy cooperative theory extension of classical decision concepts on fuzzy games is an important topic. It is known, that not every concept of classical theory has its natural counterpart for fuzzy games. At the same time some results in classical cooperative games allow to be transformed on fuzzy games with of course significant differences. In this work we aimed to establish an important in classical theory optimality principle, i.e. nucleolus on fuzzy games.
is the set of all fuzzy coalitions and v is the characteristic function of that game which maps a real number to each fuzzy coalition.Cooperative fuzzy games reflect situations in which for players allowed to take part in a coalition with participation levels that may vary from non-cooperation to full cooperation. The obtained reward in this type of games defines depending on the level of cooperation. Participation levels at which players involved in cooperation gets described by fuzzy coalitions. Aubin (1981) has been explaining use of fuzzy coalitions by following way when he first introduced them in game theory. Every player can choose his level of participation in a coalition instead of whether to participate in it or not. As an example in favor of that approach can be considered case, when individual players reluctant to invest all of the available resources in enterprise where that coalition involved. For fuzzy cooperative theory extension of classical decision concepts on fuzzy games is an important topic. It is known, that not every concept of classical theory has its natural counterpart for fuzzy games. At the same time some results in classical cooperative games allow to be transformed on fuzzy games with of course significant differences. In this work we aimed to establish an important in classical theory optimality principle, i.e. nucleolus on fuzzy games. 2. Basic Definitions and Results
- Together with fuzzy theory of nucleolus we are also going to deal with the classical version of the same concept. For that reason we need to reproduce here some preliminary facts from the classical theory of nucleolus. At the end of this paragraph we will bring the definition of nucleolus for fuzzy cooperative games.For classical cooperative games D. Schmeidler [1] has defined nucleolus as an imputation what is the best in the sense of a preference relation
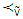 . To define the nucleolus we need the following notations. For the game
. To define the nucleolus we need the following notations. For the game 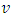 and the imputation
and the imputation 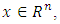 denote
denote 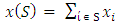 .Let
.Let 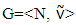 is a classical cooperative game and
is a classical cooperative game and 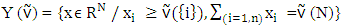 is the set of all imputations for the game G.The difference
is the set of all imputations for the game G.The difference 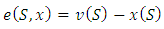 is the excess of coalition S regarding to x. Defined that way excess can be interpreted as a measure for complain of coalition S from imputation x. Let consider the vector of excesses
is the excess of coalition S regarding to x. Defined that way excess can be interpreted as a measure for complain of coalition S from imputation x. Let consider the vector of excesses 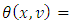
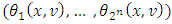 with components:
with components: From the definition of
From the definition of 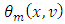 it is clear, that the components of
it is clear, that the components of 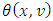 ordered decreasingly. For the game v on the set
ordered decreasingly. For the game v on the set 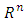 defined a quasi-order
defined a quasi-order 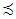 the following way. Let
the following way. Let 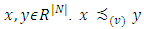 if
if 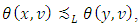 where
where 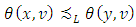 is for the lexicographical order. It means, exist a number
is for the lexicographical order. It means, exist a number 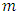 such that
such that 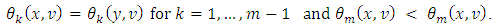 Definition 2.1 For
Definition 2.1 For 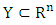 and characteristic function v, the set
and characteristic function v, the set 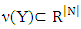 is nucleolus for Y if vectors from
is nucleolus for Y if vectors from 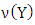 are minimal in the sense of relation
are minimal in the sense of relation 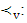 i.e.
i.e.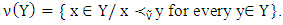 Theorem (D. Schmeidler, 1969). For every nonempty, convex and compact set the nucleolus exists and consists of only one vector. Theorem (A. Sobolev, 1976) Let for a game
Theorem (D. Schmeidler, 1969). For every nonempty, convex and compact set the nucleolus exists and consists of only one vector. Theorem (A. Sobolev, 1976) Let for a game 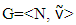 as a set of payoff vectors defined the set of pre-imputaions:
as a set of payoff vectors defined the set of pre-imputaions: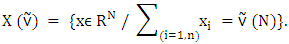 Then the game G has a nonempty pre-nucleolus
Then the game G has a nonempty pre-nucleolus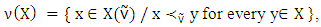 that contains only one vector. For outcomes from
that contains only one vector. For outcomes from 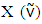 the condition of individual rationality has been violated. For that reason the set of payoff vectors
the condition of individual rationality has been violated. For that reason the set of payoff vectors 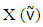 is not compact and hence, it is different of the set
is not compact and hence, it is different of the set 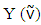 of imputations. Despite of that the statement about existence and uniqueness for pre-nucleolus continues to remain true. Fuzzy cooperative games possess infinite number of coalitions. That fact does not allow using the approach based on idea of lexicographic order to extend this concept on fuzzy games. From there arrives a need for a new definition of pre-nucleolus on fuzzy games. To be valid the needed definition should coincide with the existing one for classical games and at the same time to allow extending that concept on fuzzy cooperative games. Let (T, v) is an arbitrary fuzzy game, where
of imputations. Despite of that the statement about existence and uniqueness for pre-nucleolus continues to remain true. Fuzzy cooperative games possess infinite number of coalitions. That fact does not allow using the approach based on idea of lexicographic order to extend this concept on fuzzy games. From there arrives a need for a new definition of pre-nucleolus on fuzzy games. To be valid the needed definition should coincide with the existing one for classical games and at the same time to allow extending that concept on fuzzy cooperative games. Let (T, v) is an arbitrary fuzzy game, where 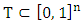 is the set of all fuzzy coalitions and
is the set of all fuzzy coalitions and 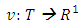 is the characteristic function of that game.Below we will prove that the newly defined pre-nucleolus coincides with already existing one. We will consider the set of only collectively rational payoff vectors, i.e. pre-imputations:
is the characteristic function of that game.Below we will prove that the newly defined pre-nucleolus coincides with already existing one. We will consider the set of only collectively rational payoff vectors, i.e. pre-imputations: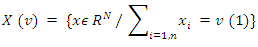 Inductively defined sets Xk, Tk by accepting that
Inductively defined sets Xk, Tk by accepting that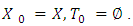 | (3.1) |
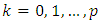 we will define sets Xk+1 the following way
we will define sets Xk+1 the following way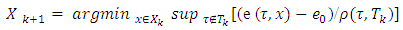 | (3.2) |
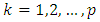
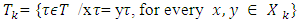 | (3.3) |
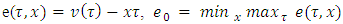 and
and 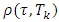 is the distance between the point
is the distance between the point 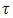 and set Tk:
and set Tk: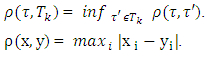 For sets
For sets 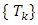 true the following: when k increases, Tk does not decrease:
true the following: when k increases, Tk does not decrease: 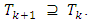 If for some k0 it is turning out that
If for some k0 it is turning out that 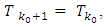 then that entails the stabilization of corresponding set
then that entails the stabilization of corresponding set 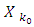 or otherwise, by increasing k, Xk does not decrease any more. The set
or otherwise, by increasing k, Xk does not decrease any more. The set 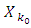 obtained that way we will call the prenucleolus for fuzzy game (T, v).
obtained that way we will call the prenucleolus for fuzzy game (T, v).3. About the Pre-Nucleolus for Classical Cooperative Games
- In this paragraph first will be described the new definition of pre-nucleolus for the set of classical cooperative games. For that type of games below has been proved that pre-nucleolus defined both of the ways coincide.Let the pair
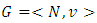 means a classical cooperative game, where
means a classical cooperative game, where 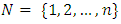 is the set of all players and
is the set of all players and 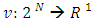 a characteristic function satisfying to the condition
a characteristic function satisfying to the condition 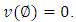 First, let pay attention that in case of classical cooperative games relations (3.1) - (3.3) accept the following view:
First, let pay attention that in case of classical cooperative games relations (3.1) - (3.3) accept the following view: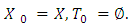 | (3.4) |
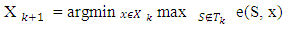 | (3.5) |
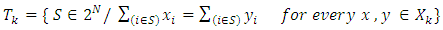 | (3.6) |
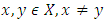 and
and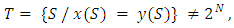 if
if 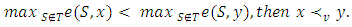 Proof: For a given vector
Proof: For a given vector 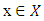 according to definition we have that
according to definition we have that 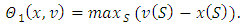 Let denote by
Let denote by 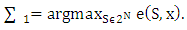 Similarly,
Similarly,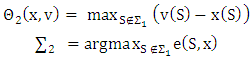 Further, for the components of
Further, for the components of 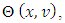 let
let 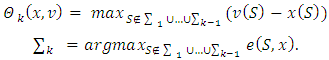 Let
Let 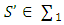 be an arbitrary coalition. If
be an arbitrary coalition. If 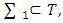 then
then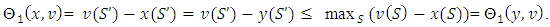 If it takes place the strong inequality then the lemma’s statement proved.We will accept now, that for all
If it takes place the strong inequality then the lemma’s statement proved.We will accept now, that for all 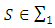 takes place only equality. Let also assume, that for some k < n
takes place only equality. Let also assume, that for some k < n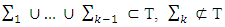 and for every
and for every 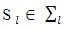 where
where 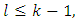
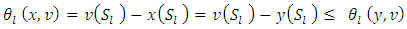 Let consider excess
Let consider excess 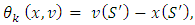 where
where 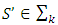 . If
. If 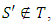 then
then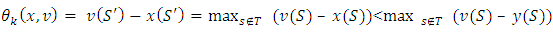
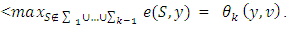 I.e.
I.e. 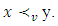 Let now
Let now 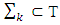 too and
too and 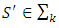 is some coalition:
is some coalition: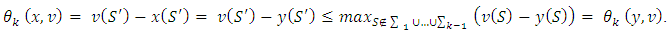 Again, if it takes place the strong inequality, then
Again, if it takes place the strong inequality, then 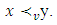 If for all k take place only equalities then x = y, which contradicts the condition of lemma.Let numbers
If for all k take place only equalities then x = y, which contradicts the condition of lemma.Let numbers 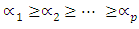 are all of different values accepted by the components of vector
are all of different values accepted by the components of vector 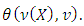 Below we will deal with the sets
Below we will deal with the sets 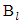 and
and 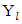 defined following way:
defined following way: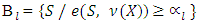
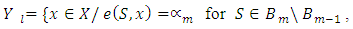
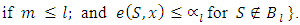 Lemma 3.2. If
Lemma 3.2. If  then
then 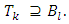 Proof. Let
Proof. Let 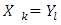 and
and 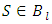 be an arbitrary coalition. It is clear, that for some
be an arbitrary coalition. It is clear, that for some 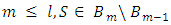 . According to definition of
. According to definition of 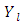 for every
for every 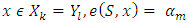 . But then
. But then 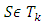 which means that
which means that 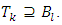 Lemma 3.3. For all
Lemma 3.3. For all 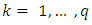 exist numbers lk and sets Xk such that Proof. For k = 1 the relation (3.7) follows from definitions of sets X1 and Y1. Accept it already has been proved that for some k and l
exist numbers lk and sets Xk such that Proof. For k = 1 the relation (3.7) follows from definitions of sets X1 and Y1. Accept it already has been proved that for some k and l 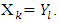 According to lemma 2 supposed to take place inclusion
According to lemma 2 supposed to take place inclusion 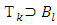 . If
. If 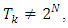 because
because 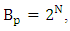 then exists
then exists 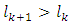 such that
such that 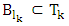 and
and 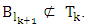 Necessary to prove that it will entail the coinsidence of sets
Necessary to prove that it will entail the coinsidence of sets 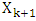 and
and 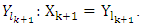 Let now for some
Let now for some 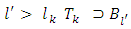 and
and 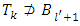 . Then will exist set
. Then will exist set 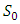 such that
such that 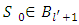 and
and 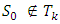 . Subsequently,
. Subsequently, 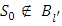 . Which means, that
. Which means, that 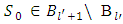 . Because
. Because 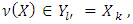 so according to lemma 3.1,
so according to lemma 3.1,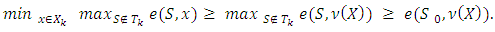 By the other side, as far as
By the other side, as far as 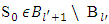 then
then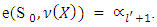 From there it follows that
From there it follows that 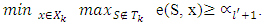 Further,
Further,  because
because 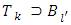 and
and 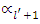 is the first value of
is the first value of 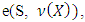 which is smaller than
which is smaller than 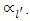 As a result,
As a result,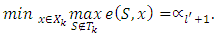 Or otherwise,
Or otherwise, 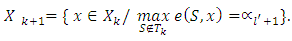 Which means, that
Which means, that 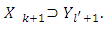 Let now prove the opposite inclusion, i.e. if
Let now prove the opposite inclusion, i.e. if 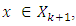 then
then 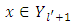 too. As far as
too. As far as 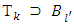 and
and 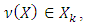 so for every
so for every 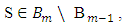 where
where 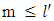
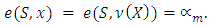 Besides that, for every
Besides that, for every 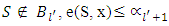 . It is remaining to proof that for arbitrary
. It is remaining to proof that for arbitrary 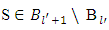
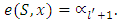 Accept that for some coalition
Accept that for some coalition 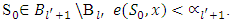 Let consider the vector
Let consider the vector 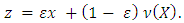 For coalitions
For coalitions 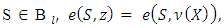 for
for 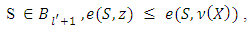 and
and 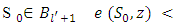
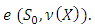 From there it follows that for a number
From there it follows that for a number 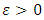 small enough, and every
small enough, and every 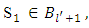
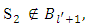
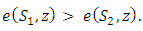 Which means that the constructed above vector
Which means that the constructed above vector 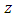 is more preferable than
is more preferable than 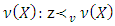 . That contradicts to the fact that ν(X) is pre-nucleolus for the game
. That contradicts to the fact that ν(X) is pre-nucleolus for the game 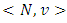 . Hence, for every
. Hence, for every 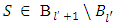 supposed to hold true the equality
supposed to hold true the equality 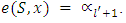 But then the received equality would mean, that
But then the received equality would mean, that 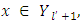 and
and 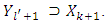 The last inclusion concludes the proof of our lemma.Theorem. 3.1 There is a number q such that
The last inclusion concludes the proof of our lemma.Theorem. 3.1 There is a number q such that 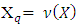 .Proof. Because
.Proof. Because 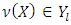 for every
for every 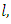 so according to lemma 3.3, we will have, that also
so according to lemma 3.3, we will have, that also 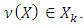 If
If 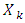 contains more than one point then it is obvious that
contains more than one point then it is obvious that 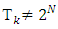 . Then based on lemma 3.3 and lemma 3.2,
. Then based on lemma 3.3 and lemma 3.2, 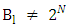 and according to lemma 1 we will be able to construct the next set
and according to lemma 1 we will be able to construct the next set 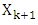 . The constructed that way last set
. The constructed that way last set 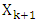 will consist of only the nucleolus
will consist of only the nucleolus 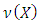 .
.4. Fuzzy Games with Finite Sets of Coalitions
- 4.1. Let
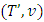 is a fuzzy cooperative game, where
is a fuzzy cooperative game, where 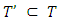 is some finite set of fuzzy coalitions. Below we will prove that in presence of some conditions this type of games possess a unique prenucleolus. Lemma 4.1. Let X is a convex polytope and χ is the solution for the next linear programming problem:
is some finite set of fuzzy coalitions. Below we will prove that in presence of some conditions this type of games possess a unique prenucleolus. Lemma 4.1. Let X is a convex polytope and χ is the solution for the next linear programming problem: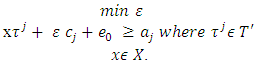 Then exists a vector
Then exists a vector 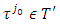 such that for every
such that for every 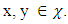 Proof. Let for every
Proof. Let for every 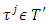 exists a vector
exists a vector 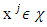 such that
such that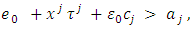 where
where 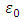 is the solution of mentioned above linear programming problem. Consider now the vector
is the solution of mentioned above linear programming problem. Consider now the vector 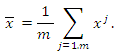 Because of convexity of the set
Because of convexity of the set 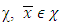 and
and 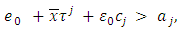 for every
for every 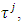 which contradicts to the condition that
which contradicts to the condition that 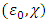 is the optimal solution for our minimization problem. So, exists a vector
is the optimal solution for our minimization problem. So, exists a vector 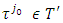 such that for every
such that for every 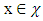
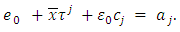 From there the assertion of lemma 3.4 follows. Theorem 4.1 Let
From there the assertion of lemma 3.4 follows. Theorem 4.1 Let 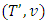 is a fuzzy game, where
is a fuzzy game, where 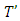 is a finite set of fuzzy coalitions that also contains coalitions
is a finite set of fuzzy coalitions that also contains coalitions 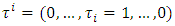 for arbitrary
for arbitrary 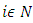 . Then the game
. Then the game 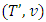 possesses a unique pre-nucleolus.Proof. We need to prove that after finite number of steps the process of construction of sets Xk, Tk will be abrupt and the last set Xk will consists of a unique point.The set X1 is solution for the following minimization problem:
possesses a unique pre-nucleolus.Proof. We need to prove that after finite number of steps the process of construction of sets Xk, Tk will be abrupt and the last set Xk will consists of a unique point.The set X1 is solution for the following minimization problem: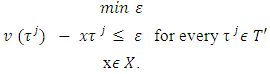 | (3.8) |
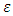 bounded below. Really, if
bounded below. Really, if 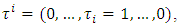 then
then 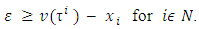 Summing all these inequalities by
Summing all these inequalities by 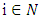 we will obtain that
we will obtain that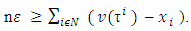 from where
from where 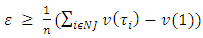 ,what has been required to prove.When
,what has been required to prove.When 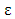 accepts its minimal value we obtain the solution of our problem:
accepts its minimal value we obtain the solution of our problem: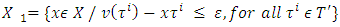 The corresponding set
The corresponding set 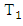 is:
is: 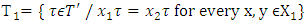 Further we need to find the
Further we need to find the 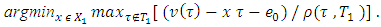 That is the same as solving the following minimization problem:
That is the same as solving the following minimization problem: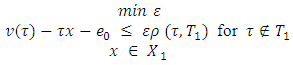 The solution X2 for this problem is a convex politope and the set T2 strictly contains the set
The solution X2 for this problem is a convex politope and the set T2 strictly contains the set 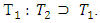 The same will take place on the following steps too. As far as the set
The same will take place on the following steps too. As far as the set 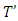 is finite, so construction of sets Xk, Tk will be abrupt after finite number of steps.Let now
is finite, so construction of sets Xk, Tk will be abrupt after finite number of steps.Let now 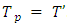 . It is remaining to prove that
. It is remaining to prove that 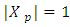 . If
. If 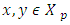 then from
then from 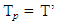 will follow that
will follow that 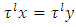 for arbitrary
for arbitrary 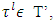 from where x = y. That concludes the proof of our theorem.4.2. Fuzzy Games with Piece-Wise Affine Characteristic FunctionsBelow proved a theorem about existence and uniqueness of pre-nucleolus for fuzzy games with piece-wise affine characteristic functions.Theorem 4.2. Let (T, v) is a fuzzy cooperative game with piece-wise affine characteristic function v. That means, exists a collection of simplexes
from where x = y. That concludes the proof of our theorem.4.2. Fuzzy Games with Piece-Wise Affine Characteristic FunctionsBelow proved a theorem about existence and uniqueness of pre-nucleolus for fuzzy games with piece-wise affine characteristic functions.Theorem 4.2. Let (T, v) is a fuzzy cooperative game with piece-wise affine characteristic function v. That means, exists a collection of simplexes 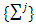 what covers
what covers 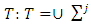 ,
, 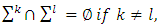 and for
and for 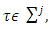
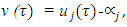 where
where 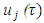 is a linear function and
is a linear function and 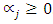 . Then the game (T, v) has a pre-nucleolus that consists of a unique point.Proof. According to definitions of sets Xk, Tk
. Then the game (T, v) has a pre-nucleolus that consists of a unique point.Proof. According to definitions of sets Xk, Tk 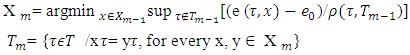 The set X1 is the solution for following minimization problem:
The set X1 is the solution for following minimization problem: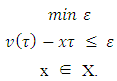 | (3.9) |

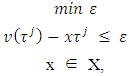
 (3.9')where the
(3.9')where the 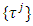 is the set of all peaks of simplexes
is the set of all peaks of simplexes 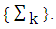 Accept that the pair
Accept that the pair 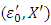 is the solution for that problem, where
is the solution for that problem, where 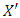 is a convex politope. It is clear that
is a convex politope. It is clear that 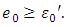 We will prove that
We will prove that 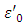 also is solution for the problem (3.9). For that reason we will need to show that the inequality
also is solution for the problem (3.9). For that reason we will need to show that the inequality 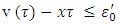 holds true for all
holds true for all 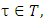 when
when 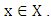 Let
Let 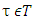 is an arbitrary coalition and
is an arbitrary coalition and 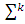 is a simplex with peaks
is a simplex with peaks 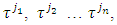 which contains
which contains 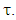 Then
Then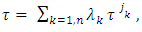 where
where 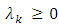 and
and 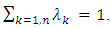 Because
Because 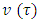 is an affine function on
is an affine function on 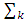 so we will have that
so we will have that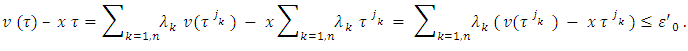 From there,
From there, 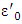 really is a solution for the problem (3.9). So, we will have that X1 is the following set:
really is a solution for the problem (3.9). So, we will have that X1 is the following set: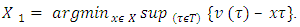 According to definition of sets
According to definition of sets 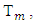 for a fixed
for a fixed 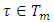 and every
and every 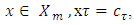 what means that the product
what means that the product 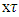 is constant for every
is constant for every 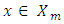 . Let now
. Let now 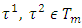 are such coalitions that
are such coalitions that 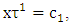 and
and 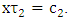 From there it will follow that if for some numbers
From there it will follow that if for some numbers 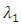 and
and 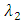
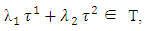 then for every
then for every 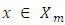
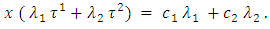 The latter one means that set Tm is the intersection of the set of all coalitions T with some hyperplane and subsequently is a convex set, because of convexity of T.Next we will rewrite the definition of
The latter one means that set Tm is the intersection of the set of all coalitions T with some hyperplane and subsequently is a convex set, because of convexity of T.Next we will rewrite the definition of 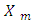 in a different form:
in a different form: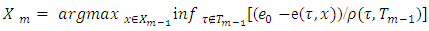 The set
The set 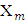 defined that way is solution for the following maximization problem:
defined that way is solution for the following maximization problem: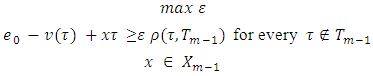 | (3.10) |
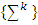 that does not belong to Tm-1:
that does not belong to Tm-1:
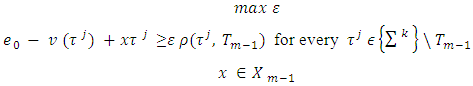
 (3.10’)The problem (3.10’) has a solution because it is a linear programming problem and Xm-1 is a convex polytope. Let denote that solution by
(3.10’)The problem (3.10’) has a solution because it is a linear programming problem and Xm-1 is a convex polytope. Let denote that solution by 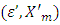 and prove that inequalities (3.10’) remain true for all
and prove that inequalities (3.10’) remain true for all 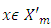 and
and 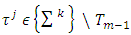 . For
. For 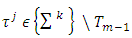 the inequality (3.10’) follows from definition of sets Xm. For
the inequality (3.10’) follows from definition of sets Xm. For 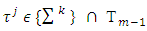 (3.10’) is true because for that kind of
(3.10’) is true because for that kind of 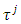 the right side of (5’) is equal to 0 and the left side is not negative as far as
the right side of (5’) is equal to 0 and the left side is not negative as far as 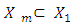 .Let now
.Let now 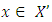 and
and 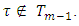 Accept that
Accept that 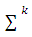 is a simplex for what
is a simplex for what 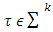 and
and 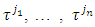 are peaks for that simplex. According to the Karatheodory’s theorem:
are peaks for that simplex. According to the Karatheodory’s theorem: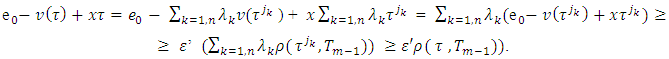 The last inequality in the chain above takes place because of convexity of metric
The last inequality in the chain above takes place because of convexity of metric 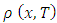 by the variable
by the variable 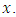 As a result, has been proved that the solution
As a result, has been proved that the solution 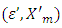 for the problem (3.10’) also is solution for (3.10). From there according to lemma 4.1 exists
for the problem (3.10’) also is solution for (3.10). From there according to lemma 4.1 exists 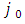 such that
such that 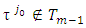 and for arbitrary
and for arbitrary 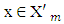 takes place equality in (3.10’). Then because
takes place equality in (3.10’). Then because 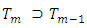 and
and 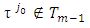 so
so 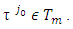 As a result to that the dimension of Tm will increase by at least one. From there because as its proved above the sets Tm are convex, so after finite number of steps Tm will coincide with T and the corresponding set
As a result to that the dimension of Tm will increase by at least one. From there because as its proved above the sets Tm are convex, so after finite number of steps Tm will coincide with T and the corresponding set 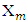 will contain only one point.4.3. An Example for Calculation of Pre-NucleolusThe paragraph below devoted to finding of the pre-nucleolus for fuzzy game from a parameterized class. Let considered a game
will contain only one point.4.3. An Example for Calculation of Pre-NucleolusThe paragraph below devoted to finding of the pre-nucleolus for fuzzy game from a parameterized class. Let considered a game 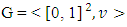 with the following characteristic function
with the following characteristic function 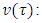
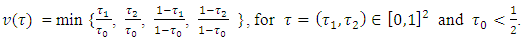 It is clear that for this game v(1) =1 and
It is clear that for this game v(1) =1 and 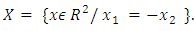 Solving of the problem will start from dividing the square
Solving of the problem will start from dividing the square 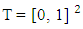 on eight triangle subsets and figureing out values of
on eight triangle subsets and figureing out values of 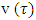 on each one of them. Let denote these subsets by
on each one of them. Let denote these subsets by 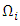 (i =1… 8) and start to describe them.
(i =1… 8) and start to describe them.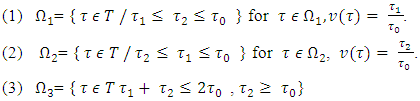 Based on inequalities that define
Based on inequalities that define 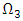 it is obtained that
it is obtained that 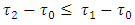 and
and 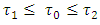 from there
from there 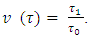
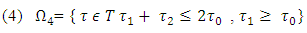 For
For 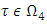 are true the following inequalities:
are true the following inequalities: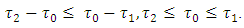 From what it follows that
From what it follows that 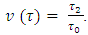
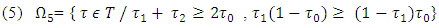 The definition of
The definition of 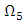 implies that for
implies that for 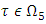 hold true the inequalities:
hold true the inequalities: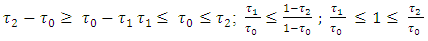 So, for
So, for 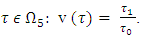
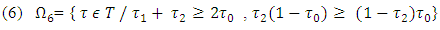 Analogically to
Analogically to 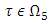 in this case too
in this case too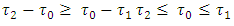 Further, because
Further, because 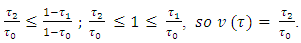
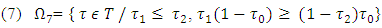 From inequalities that define
From inequalities that define 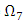 follows that for
follows that for 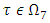
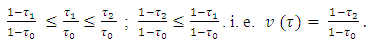
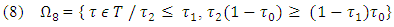 On
On 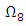 hold true the following inequalities:
hold true the following inequalities: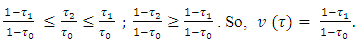 To find sets X1 and T1 enough to calculate the following magnitude:
To find sets X1 and T1 enough to calculate the following magnitude: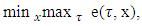 where
where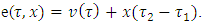 Let now to calculate the magnitude of
Let now to calculate the magnitude of 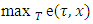 by the scheme below:
by the scheme below: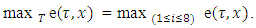 Further by turn will be figured out magnitudes of the following inner maximums:
Further by turn will be figured out magnitudes of the following inner maximums: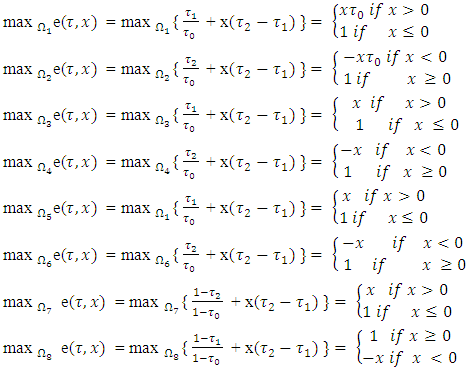 Now, when the values for
Now, when the values for 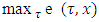 by subsets
by subsets 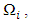 already have been found can be calculated value for the preliminary expression:
already have been found can be calculated value for the preliminary expression: 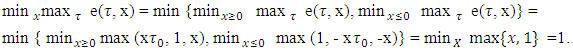 Further, because for x with
Further, because for x with 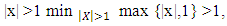 so from there it is clear that
so from there it is clear that 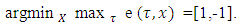 That value together with definition of the set
That value together with definition of the set 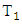 gives that
gives that 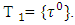 Let denote
Let denote 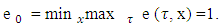 To find sets X2, T2 should be calculated the magnitude of
To find sets X2, T2 should be calculated the magnitude of 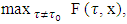 where
where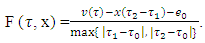 The magnitude of
The magnitude of 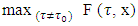 also will be calculated by subsets
also will be calculated by subsets 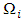 , the same way as it has been done with the
, the same way as it has been done with the 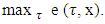
 At the end it is remaining to calculate one more magnitude, which will give us the set X2:
At the end it is remaining to calculate one more magnitude, which will give us the set X2: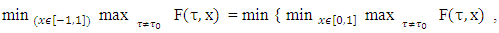
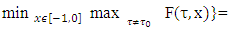
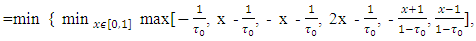
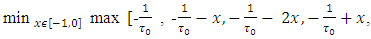
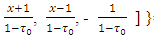
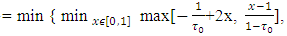
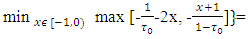
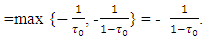 So, as a result it obtaines that
So, as a result it obtaines that 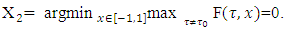 From there for the pre-nucleolus v(X) of initial game it follows that
From there for the pre-nucleolus v(X) of initial game it follows that 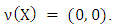
Note
- 1) Results that included in this paper have been part of author’s doctoral dissertation written in early 1990’s. There is available a copyright certificate from the US Copyright Office.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML